当前位置：首页 > news >正文

排序--快排--Hoare法

news 来源：原创 2025/5/1 6:29:19

一，引言

快速排序作为基础排序中的一种，在其优秀的时间复杂度，在实践中有着重要意义，因此我们非常有必要去学习快排的底层逻辑和代码实现。

下面我将从下面几个方面进行讲解，逻辑讲解，代码实现，代码优化，时间复杂度，空间复杂度，稳定性等方面。

二，逻辑讲解：

首先来看一组动图：

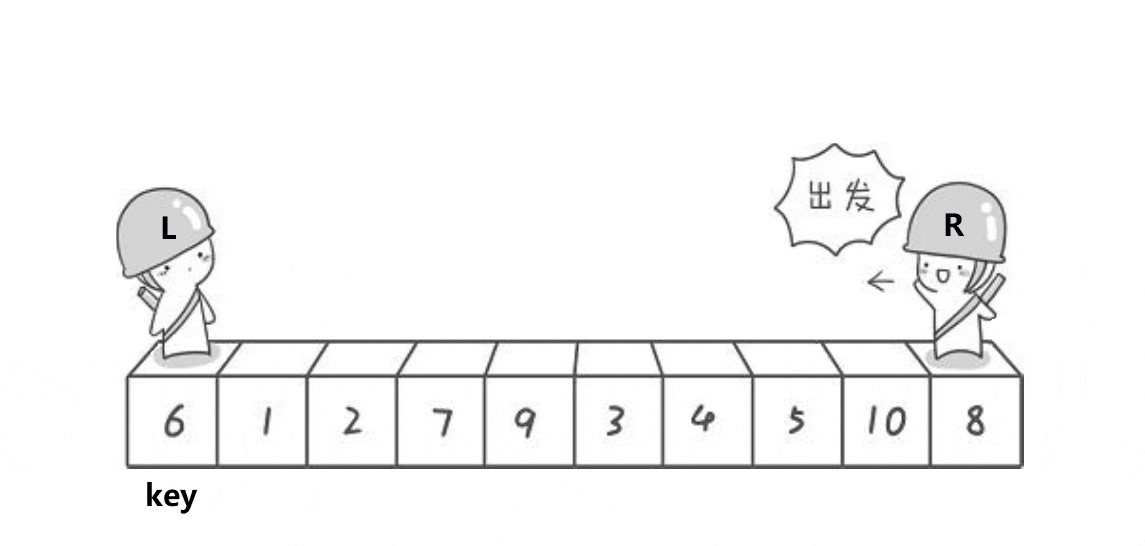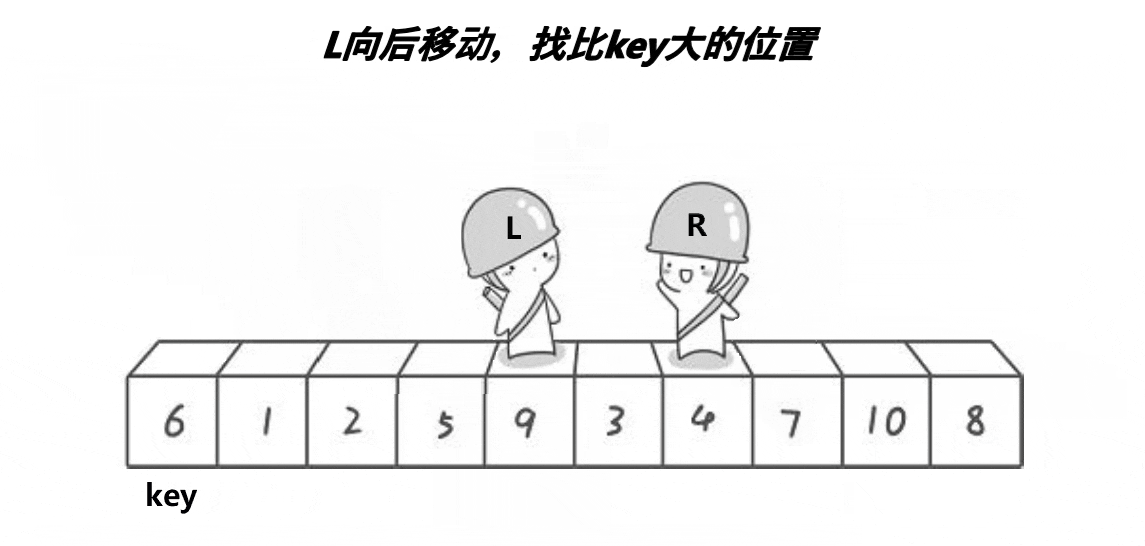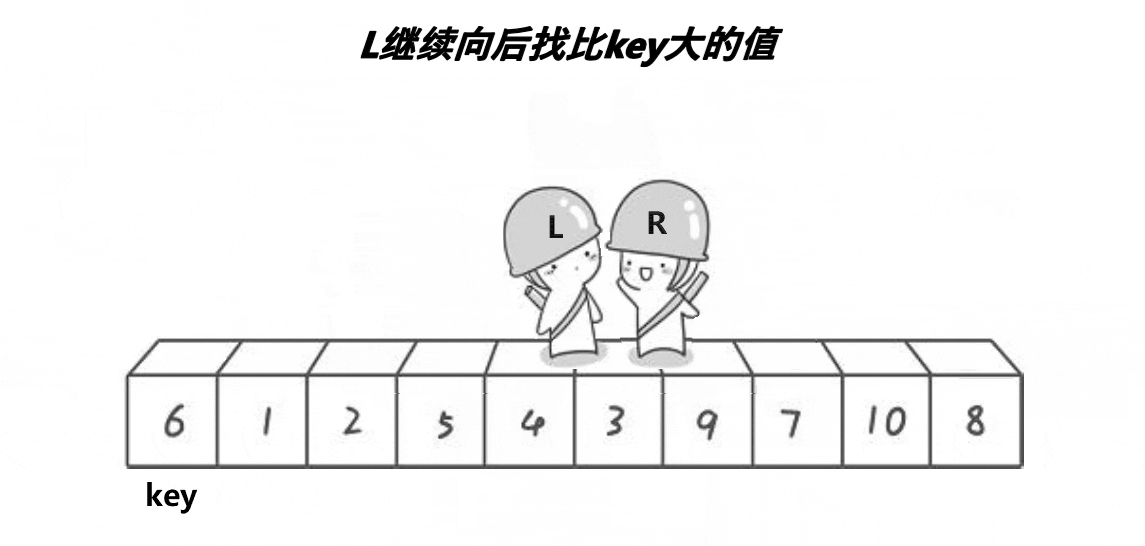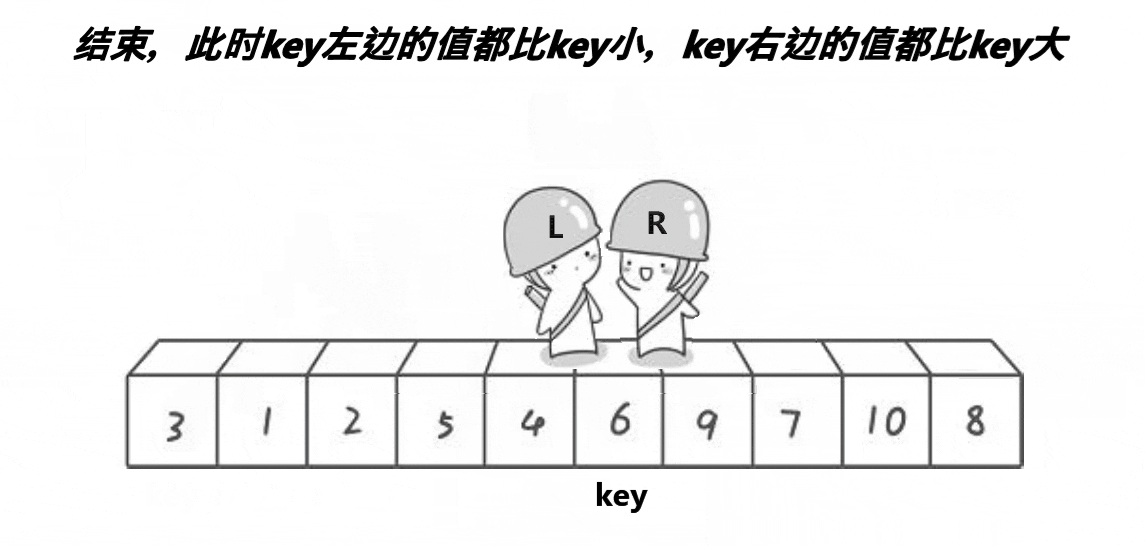
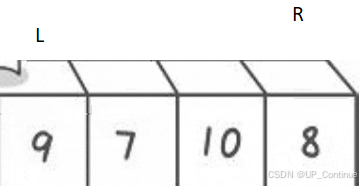
通常来说选择最左边数据或最右边数据为关键字（key），就以动图中的数据为例进行一步步讲解

第一趟：

首先从最右边出发（R）向前走找到比key小的数据停下：

此时R保持不动，L开始出发找比key大的数据：

找到之后进行数据的交换：

之后同样上述操作，直到两者相遇，相遇的的位置与key的位置进行交换：

单趟排序结束。

第二趟：

第二趟将该数组分成两组第一组[L,key-1]，第二组[key+1,R]

左半边key+1变成了新的R，数据3成为了新的key。

右半边key+1变成了新的L，数据9成为了新的Key。

此时新的两组数据进行相同的排序方法，直到最后一个数据，或者没有数据，排序结束。这个过程使用递归去完成-----通过传入不同的L和R。来进行不同排序。

我具体画一下第一部分的展开图：

第一次排序结束：进行分组。

第二次排序：

排序开始：

排序结束，继续进行分组:

此时key的右分支没有数据，左分支之一一个数据，排序结束。

总结：

这是一个递归的过程，我仅仅呈现左半组的排序过程，大家可以把整个数组的递归展开的图画出来，有助于对快拍有着更加深入的理解。

三，代码实现

在代码实现之前，要思考下面几个问题：
1，L和R什么时候结束，有哪几种结束方式。

2，什么时候结束递归结束。

下面的代码仅供参考：

void QuickSort(int* p, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int begin = left;
	int end = right;
	int keys = begin;

	while (begin != end)
	{
		while ((p[keys] <= p[end])&&begin != end)
		{
			end--;
		}
		while ((p[keys] >= p[begin]) && begin != end)
		{
			begin++;
		}
		swap(&p[begin], &p[end]);
	}
	swap(&p[begin], &p[keys]);
	keys = begin;
	QuickSort(p, left, keys - 1);
	QuickSort(p, keys+1, right);


}

强调几个点：
1，一定要进行相遇的判断，否则可能出现交叉错过的情况。

2，交换keys和begin的值之后，要记得将keys重新进行赋值。

四，代码优化

1，三数取中：
当一些特殊数据会呈现极端的情况，key的值能是最小或者最大，这样子会大大增加递归的深度，在排序之前进行一个三数取中，将中间的数作为新的key值，可以减少出现极端情况的次数。

代码样例：

//三数取中
int small = p[left];
int big = p[right];
int mid = p[(small + big) / 2];
if (small > big && small > mid)
{
	if (big > mid)
	{
		mid = big;
	}
}
else if (big > mid && big > small)
{
	if (small > mid)
	{
		mid = small;
	}
}
else
{
	if (big > small)
	{
		mid = big;
	}
	else
	{
		mid = small;
	}
}

swap(&p[left], &p[mid]);

2，当数据量过小时，不需要一直递归，可以将剩下的使用插入排序进行排序。