Transformer原理
目录
一、简单介绍
二、基本结构
三、详细拆解
前言
注意力机制
自注意力:缩放点积注意力计算
交叉注意力:
多头注意力:每一个头做的都是缩放点积注意力
位置编码
四、模型框架
encoder
多头注意力:将QKV分为h组(一般为8),每组独立计算注意力后拼接结果
前馈神经网络:由两层全连接层和ReLU激活函数,每个子层后接残差连接和层归一化
残差处理:Output=Sublayer(x)+x 在输出后直接叠加该子层的输入
层归一化:在残差处理后对结果归一化,对每个样本独立计算均值和方差
decoder
掩码多头注意力层:创建一个下三角矩阵,左下方全是0,右上方负无穷
编码器-解码器多头注意力层(交叉注意力)
前馈神经网络
五、一点提醒(位置编码)
举例
一、简单介绍
相对于seq2seq就是不使用循环RNN,训练的时候可以并行训练,这个时候如果把句子加的很长,数据集用的很大也可以。Transformei是一个N近N出的结构,每个Transformer单元相当于一层的RNN,接收一整个句子所有词作为输入,然对每一个词都做输出。Transformer任意两个词之间的操作距离都是1。
二、基本结构
主要分为编码和解码两个部分,每个encoder和decoder又是一个串联的组合,比如输入了以后经过6个编码器,右边通过6的解码器输出,可以理解为每次完整的变形都要重复2*6步操作,每个encoder又包含self-attention和前馈网络两个模块,分别计算权重和根据权重变形。decoder在self-attention和前馈神经网络中间还增加了一层encoder-decoder attention,作用就是在解码时不仅看翻译内容还要看上下文信息。每个self-attention会分解为Multi-head attention。

三、详细拆解
前言
如果设计纯粹语义关系的编码,数字化之后的数值要能体现语义关系。就比方说现在有学生和书和大象,那么可以假设学生和书这两个语义关系的向量在空间中的距离更近,而与大象更远。
数字化方法一种是分词器,一种是独热编码,分词器Tokenizer是一个用于向量化文本,将文本转换为序列的类,可以把文本投射到一维空间,完全没有利用维度关系。而one-hot投射到多维空间,有多少单词就是多少维空间,每个向量正交,没有把空间的长度利用起来,很难体现出单词之间的联系,所以One-hot并不适合在此使用。
所以我们要找到一个浅空间,一种方法是升维,一种是降维。而通过矩阵相乘就可以实现降维,可以看作空间变换。向量的一行和矩阵的一列相乘得到一个数:

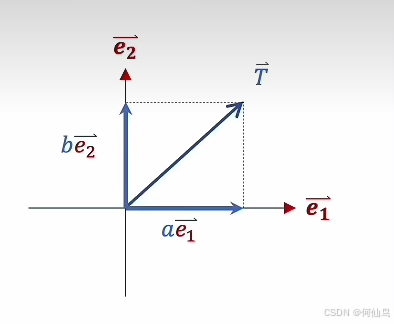
假如T向量是操作之前的向量,这个向量里的每一个数值就相当于对应坐标系下的坐标值,也就是在e1和e2上的分量比如be1,ae2,而通过与矩阵相乘以后就可以在一个新的坐标系下表示,坐标轴可以看作单位向量,那么在新坐标系下,比如原本是be1,e1=(w1,w2),现在在这个坐标系下e1=(w11,w12,w13),那么T的e1的分量就可以表示为(bw11,bw12,bw13),e2同理。总结就是行代表旧坐标系有多少维度,列代表新坐标系有多少维度。但是向量与矩阵相乘也会发生拉伸和收缩,变的是向量,当他们结合起来,就可以在新的坐标系下产生向量的变换


如果想让一个直线经过矩阵相乘变成一个曲线,就需要通过二次型。众所周知二次型P(x)=XtAX,那么这里x就是原本的向量,对应的就是一个二次函数:

原来空间中的向量经过矩阵相乘之后就可以变成新空间里的数据,同理多个向量也可以如此,那么就是矩阵和矩阵相乘。
一个神经网络的隐藏层其实就是在做一次线性变化:

其中隐藏层的神经元个数就是变换后空间的维度,输入的多就是升维,反之降维。举个例子:当数据从两维的经过升维编程十维,如图:

如果这是分类问题,如果数据只是二维的,那么坐标系中很难用一条直线来进行划分,那么只有在更高的维度中才能实现更好的划分,只要维数高就可以找到一个平面划分。隐藏层的作用就是让数据更复杂。当隐藏层的层数变多,如果每层的维度越来越少,相当于降维,这是因为某个特征不需要原始数据里的所有维度,只需要关注某个特征就可以,可以理解为对上一层进行了抽象,至于为什么需要那么多层隐藏层,这是因为可以更好的利用基础的特征部分,可以复用,隐藏层越深,抽象程度越高。
再说说embedding,每一个维度都代表了一个语义,具体的语义是什么要看数据:

潜空间可以联系上下文,而翻译手册不行。
注意力机制
注意力机制就是下图橙色的部分:

自注意力:缩放点积注意力计算
一组词向量,通过分别和三个矩阵相乘之后分别会得到QKV,然后进行运算。注意力要解决的就是整体语义,考虑一组词的情况。自注意力机制:

Q和K相乘其实就是一个向量在另一个向量上面的投影,可以表达他们之间的关系,的带的A就是他们的点积,就比如如果他们的共线的,那么cos就是1:

内积运算的结果就是关系,对他们sofmax之后,数值还是代表他们词之间的关系,下图右边矩阵的v还是代表一个词向量,相乘之后仍然是相同行数相同列数的矩阵但是经过修正,这样比如v'22能对它产生影响的就是那一列所有的词向量,相同维度的才会产生影响:

总结就是Q和K先得到一组词向量自己和自己间的关系然后再去修正,修正后的词向量都是根据上下文修正后的,所以多个词向量叠加在一起就增加了主观性。
除以根号Dk(K的维度)是因为点积的值过大会导致softmax函数的输入值过大,从而使softma x的输出接近一个one-hot向量(梯度太小)。同时可以将点积的方差控制为1.

那么,为什么要用两个矩阵而不是一个去训练呢,是因为如果是一个矩阵的话,通过权重矩阵相乘,它得到的是线性变化,只能表示线性关系,如果是两个句子相乘,那看起来就很像二次型了,可以看作一个高维度版本,拥有更强的表达能力,也是相当于加入一些非线性因素。
那为什么要把Q和K单独表示呢,因为Q和K可以刚好承担主观语义的两种功能。就像条件语句。
交叉注意力:
交叉注意力Q和V生成的数据不一样。在不同序列之间建立注意力,例如解码器用自身生成的查询(Query)去关注编码器的键(Key)和值(Value)。
多头注意力:每一个头做的都是缩放点积注意力

分别计算三次,三个矩阵里面的系数不一样,多头注意力机制就是把他们拼起来拼成一个大矩阵,再和一个w相乘,然后得到一个输出的词向量。
位置编码

输入的词向量需要指明先后顺序,一种可以通过乘法一种通过加法,添加位置信息,原版的transformer选择用加法,防止乘法导致的位置带来的权重太大,但不代表不能使用乘法。
绝对位置编码:

现在需要升维,那么每一行就是这样,P作为分母就是周期,很像傅里叶级数,那么可以假设前面的系数都是1,并且可以把项变为有限的:
可以把函数想成向量S和C,那么拼在一起就是一个更大的向量,所有词向量对应的写下来就是P矩阵:


正交就是说线性无关。
使用f(t)可以让token之间的频率相对的差距尽可能的大。所以用这个函数的好处可以让fx的周期更大,可以同时输入更多的token,而且相对关系从距离变成了旋转角度:

在P矩阵中:

加了P之后:

展开之后只有第一项和之前的是一样的,后面三项都和P矩阵有关,这也是一种叠加方式,可以看成四个矩阵叠加在一起,只有第一个矩阵和数据有关,其他和位置有关。
四、模型框架
Transformer由encoder和decoder构成,一般都有6个相同层
encoder
每层encoder包含两个子层:多头注意力层和前馈神经网络层。
多头注意力:将QKV分为h组(一般为8),每组独立计算注意力后拼接结果
前馈神经网络:由两层全连接层和ReLU激活函数,每个子层后接残差连接和层归一化
残差处理:Output=Sublayer(x)+x 在输出后直接叠加该子层的输入
层归一化:在残差处理后对结果归一化,对每个样本独立计算均值和方差
Transformer处理变长序列,同一批次内长度可能不同,pad会导致BN偏差,所以用LN

decoder
每层decoder包含三个子层:带掩码的多头注意力层(防止解码时看见未来信息),编码器-解码器注意力层(连接encoder输出),前馈神经网络(也使用残差连接和层归一化)
掩码多头注意力层:创建一个下三角矩阵,左下方全是0,右上方负无穷

那么计算注意力的时候就用上掩码:

然后合并,残差连接,层归一化。
此外注意,训练阶段,输入来源是目标序列的嵌入向量(右移一位,防止信息泄露)+位置编码。在推理阶段,输入是已生成的部分序列+位置编码
编码器-解码器多头注意力层(交叉注意力)
将编码器的信息整合到解码器中,这个时候,Q来自解码器上一子层,K和V来自编码器,其余步骤相同。
前馈神经网络
五、一点提醒(位置编码)
位置编码用于向模型输入序列的位置信息,通过位置编码为每个位置生成唯一的向量,与embedding相加,使模型能感知词的位置。

pos:词在序列中的位置
d:模型维度
举例
输入:["我","爱","AI"] 位置索引为0,1,2
假设词向量嵌入维度d=4
生成位置编码:
比如位置0的编码POS=0:
带入上面公式,那么四个维度的位置编码分别为sin0,cos0,sin0,cos0也就是[0,1,0,1]
再如位置1的编码:在维度0,就是sin(1/10000^(0/4))=sin1;在维度1,就是cos(1/10000^(0/4))=cos1
这里的话虽然维度1看似比维度0大了一个维度,但对于维度0,2i=0,i=0;对于维度1,2i+1=1,i=0,所以只是前面的sin和cos换了,后面的不变
