LeetCode BFS解决FloodFill算法
Flood Fill 算法是一种用于填充连通区域的算法,常用于图像处理、绘图工具中的“油漆桶”工具,以及解决迷宫、岛屿问题等。它的核心思想是从一个起始点开始,向四周扩散,填充所有符合条件的区域。
算法思想:
- 起始点:选择一个起始点(通常是某个像素或网格单元)。
- 填充条件:定义填充的条件(例如,填充与起始点颜色相同或满足某种属性的区域)。
- 扩散方式:从起始点开始,向四周(上下左右或更多方向)递归或迭代地填充符合条件的区域。
实现方式:
- 深度优先搜索(DFS):
- 使用递归或栈实现。
- 从起始点开始,向四周扩散,直到所有符合条件的区域都被填充。
- 适合小规模数据,但递归深度过大时可能导致栈溢出。
- 广度优先搜索(BFS):
- 使用队列实现。
- 从起始点开始,按层次向四周扩散。
- 适合大规模数据,不会出现栈溢出问题。
简单
733. 图像渲染
有一幅以
m x n的二维整数数组表示的图画image,其中image[i][j]表示该图画的像素值大小。你也被给予三个整数sr,sc和color。你应该从像素image[sr][sc]开始对图像进行上色 填充 。为了完成 上色工作:
- 从初始像素开始,将其颜色改为
color。- 对初始坐标的 上下左右四个方向上 相邻且与初始像素的原始颜色同色的像素点执行相同操作。
- 通过检查与初始像素的原始颜色相同的相邻像素并修改其颜色来继续 重复 此过程。
- 当 没有 其它原始颜色的相邻像素时 停止 操作。
最后返回经过上色渲染 修改 后的图像 。
示例 1:
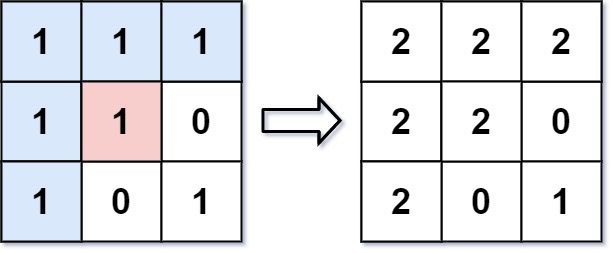
**输入:**image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, color = 2
输出:[[2,2,2],[2,2,0],[2,0,1]]
**解释:**在图像的正中间,坐标
(sr,sc)=(1,1)(即红色像素),在路径上所有符合条件的像素点的颜色都被更改成相同的新颜色(即蓝色像素)。注意,右下角的像素 没有 更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。
示例 2:
**输入:**image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
输出:[[0,0,0],[0,0,0]]
**解释:**初始像素已经用 0 着色,这与目标颜色相同。因此,不会对图像进行任何更改。
提示:
m == image.lengthn == image[i].length1 <= m, n <= 500 <= image[i][j], color < 2^160 <= sr < m0 <= sc < n
const int dx[4] = {1, -1, 0, 0};
const int dy[4] = {0, 0, 1, -1};
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
int old_color = image[sr][sc];
if (old_color == color) {
return image;
}
int m = image.size(), n = image[0].size();
queue<pair<int, int>> que;
que.emplace(sr, sc);
image[sr][sc] = color;
while (!que.empty()) {
auto [x, y] = que.front();
que.pop();
for (int i = 0; i < 4; ++i) {
int nx = x + dx[i], ny = y + dy[i];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && image[nx][ny] == old_color) {
image[nx][ny] = color;
que.emplace(nx, ny);
}
}
}
return image;
}
中等
130. 被围绕的区域
给你一个
m x n的矩阵board,由若干字符'X'和'O'组成,捕获 所有 被围绕的区域:
- **连接:**一个单元格与水平或垂直方向上相邻的单元格连接。
- 区域:连接所有
'O'的单元格来形成一个区域。- **围绕:**如果您可以用
'X'单元格 连接这个区域,并且区域中没有任何单元格位于board边缘,则该区域被'X'单元格围绕。通过 原地 将输入矩阵中的所有
'O'替换为'X'来 捕获被围绕的区域。你不需要返回任何值。示例 1:
**输入:**board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
输出:[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
解释:
在上图中,底部的区域没有被捕获,因为它在 board 的边缘并且不能被围绕。
示例 2:
**输入:**board = [[“X”]]
输出:[[“X”]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]为'X'或'O'
从矩形四周遍历,如果是字符'O',则将它标记为'F',后续进行BFS遍历所有未被包围的字符'O',最后再将被标记的字符'F'还原为字符'O',未被标记的字符'O'改为字符'X'。
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};
void solve(vector<vector<char>>& board) {
int m = board.size(), n = board[0].size();
queue<pair<int, int>> que;
for (int i = 0; i < m; ++i) {
if (board[i][0] == 'O') {
que.emplace(i, 0);
board[i][0] = 'F';
}
if (board[i][n - 1] == 'O') {
que.emplace(i, n - 1);
board[i][n - 1] = 'F';
}
}
for (int i = 1; i < n - 1; ++i) {
if (board[0][i] == 'O') {
que.emplace(0, i);
board[0][i] = 'F';
}
if (board[m - 1][i] == 'O') {
que.emplace(m - 1, i);
board[m - 1][i] = 'F';
}
}
while (!que.empty()) {
auto [x, y] = que.front();
que.pop();
for (int k = 0; k < 4; ++k) {
int nx = x + dx[k], ny = y + dy[k];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] == 'O') {
que.emplace(nx, ny);
board[nx][ny] = 'F';
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (board[i][j] == 'F') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
200. 岛屿数量
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1示例 2:
输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
for循环遍历数组,每遇到一个字符'1',通过BFS遍历上下左右所有的字符'1',标记为已遍历,并且ans++。
通过将访问过的陆地标记为 '0',可以避免额外的 visited 数组。
const int dx[4] = {1, -1, 0, 0};
const int dy[4] = {0, 0, 1, -1};
int numIslands(vector<vector<char>>& grid) {
int m = grid.size(), n = grid[0].size();
queue<pair<int, int>> que;
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
ans++;
que.emplace(i, j);
grid[i][j] = '0';
while (!que.empty()) {
auto [x, y] = que.front();
que.pop();
for (int k = 0; k < 4; ++k) {
int nx = x + dx[k], ny = y + dy[k];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == '1') {
grid[nx][ny] = '0'; // 立即修改,否则可能会导致重复入队
que.emplace(nx, ny);
}
}
}
}
}
}
return ans;
}
695. 岛屿的最大面积
给你一个大小为
m x n的二进制矩阵grid。岛屿 是由一些相邻的
1(代表土地) 构成的组合,这里的「相邻」要求两个1必须在 水平或者竖直的四个方向上 相邻。你可以假设grid的四个边缘都被0(代表水)包围着。岛屿的面积是岛上值为
1的单元格的数目。计算并返回
grid中最大的岛屿面积。如果没有岛屿,则返回面积为0。示例 1:
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]为0或1
与这题类似200. 岛屿数量,只不过每次统计一下岛屿的大小并保留最大值。
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};
int maxAreaOfIsland(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
queue<pair<int, int>> que;
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
que.emplace(i, j);
grid[i][j] = 0;
int cnt = 0;
while (!que.empty()) {
cnt++;
auto [x, y] = que.front();
que.pop();
for (int k = 0; k < 4; ++k) {
int nx = x + dx[k], ny = y + dy[k];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == 1) {
que.emplace(nx, ny);
grid[nx][ny] = 0;
}
}
}
ans = max(ans, cnt);
}
}
}
return ans;
}