《深入浅出计算机组成原理》学习笔记 Day9

1. 顺序乘法

以 $13\times 9$为例，$13_{10}=1101_2,9_{10}=1001_2$。用列竖式的方式计算：

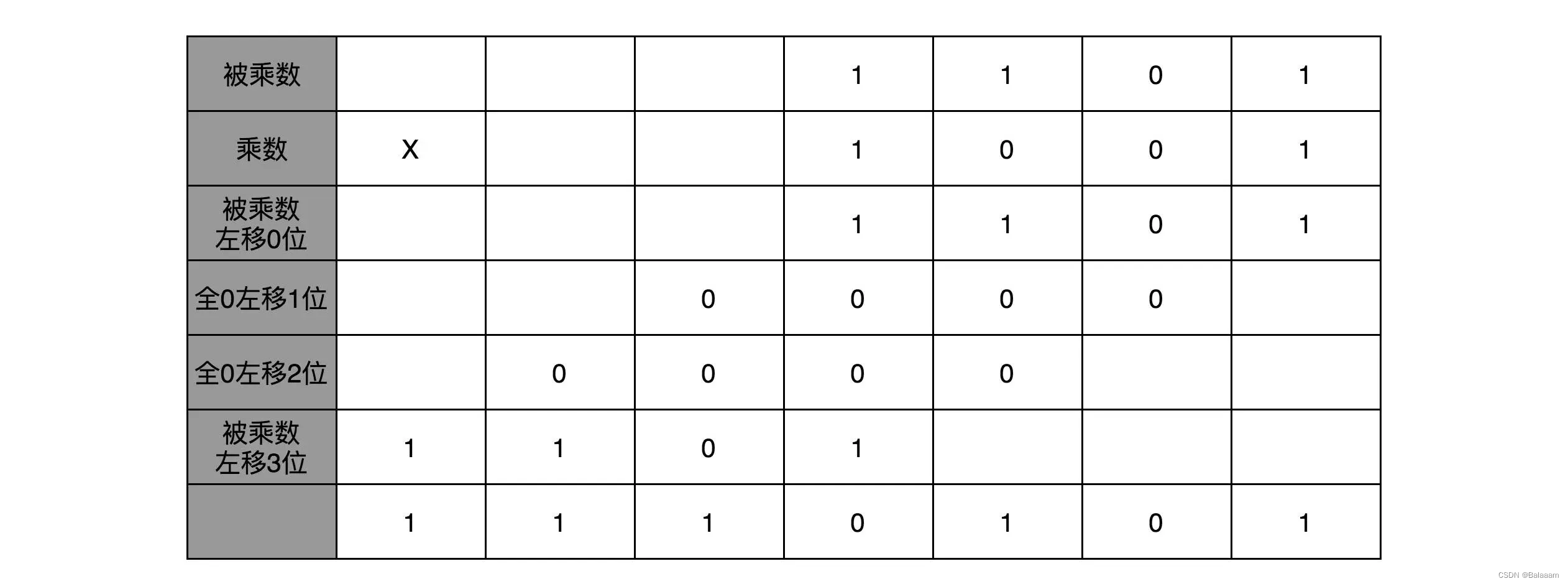
在二进制下，由于只有 0 和 1，计算机不需要去“背诵”九九乘法表，即不要单独实现一个更复杂的电路，通过 移位 和 加法 就能实现乘法。

为了节省晶体管的数量，实际上，像 $13\times 9$ 这样两个四位数的乘法，我们不需要把四次单位乘法的结果，用四组独立的开关单独都记录下来，然后再把这四个数加起来。因为这样做，需要很多组开关，如果我们计算一个 32 位的整数乘法，就要 32 组开关，太浪费晶体管了。如果我们顺序地来计算，只需要一组开关就好了。

先拿乘数最右侧的个位乘以被乘数，然后把结果写入用来存放计算结果的开关里面，然后，把被乘数左移一位，把乘数右移一位，仍然用乘数去乘以被乘数，然后把结果加到刚才的结果上。反复重复这一步骤，直到不能再左移和右移位置。这样，乘数和被乘数就像两列相向而驶的列车，仅仅需要简单的加法器、一个可以左移一位的电路和一个右移一位的电路，就能完成整个乘法。

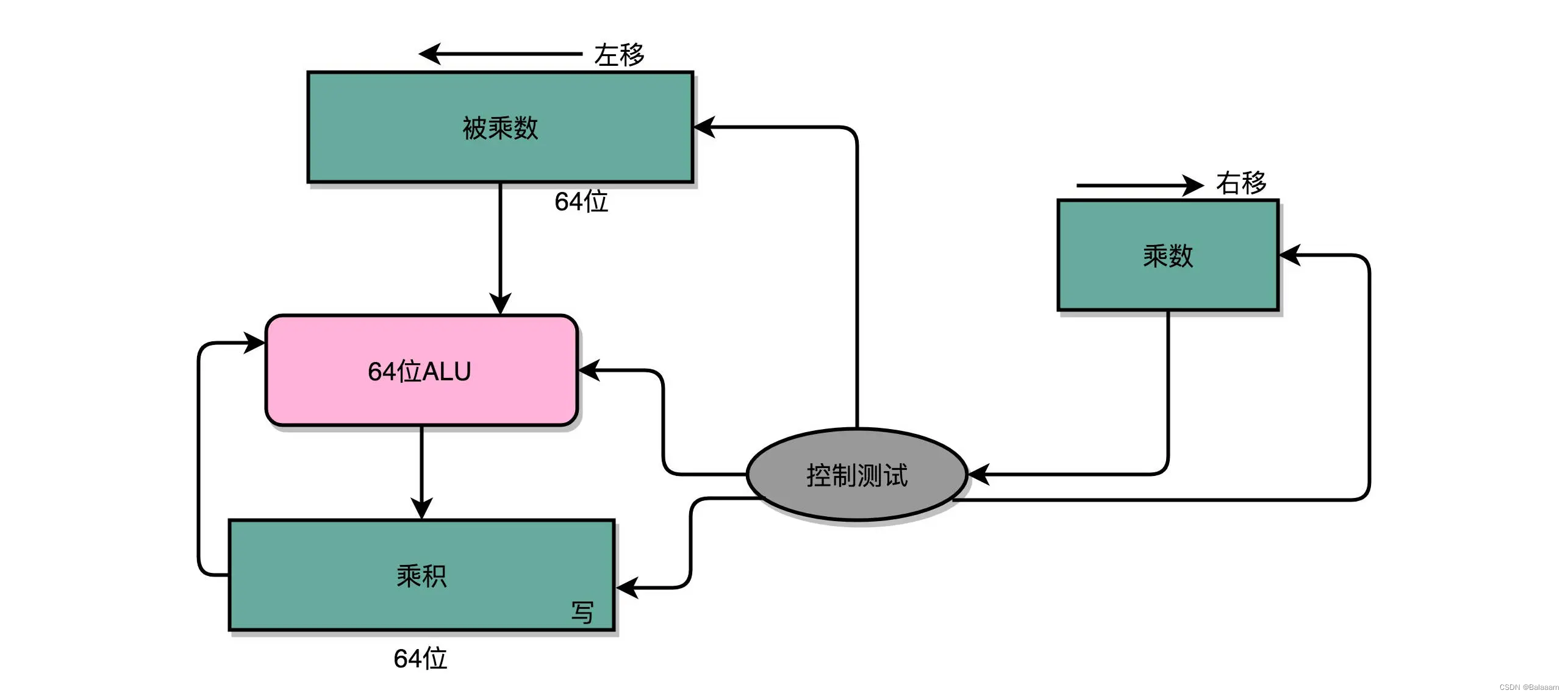
通过这个电路来计算 $13\times 9$，具体计算过程如下：

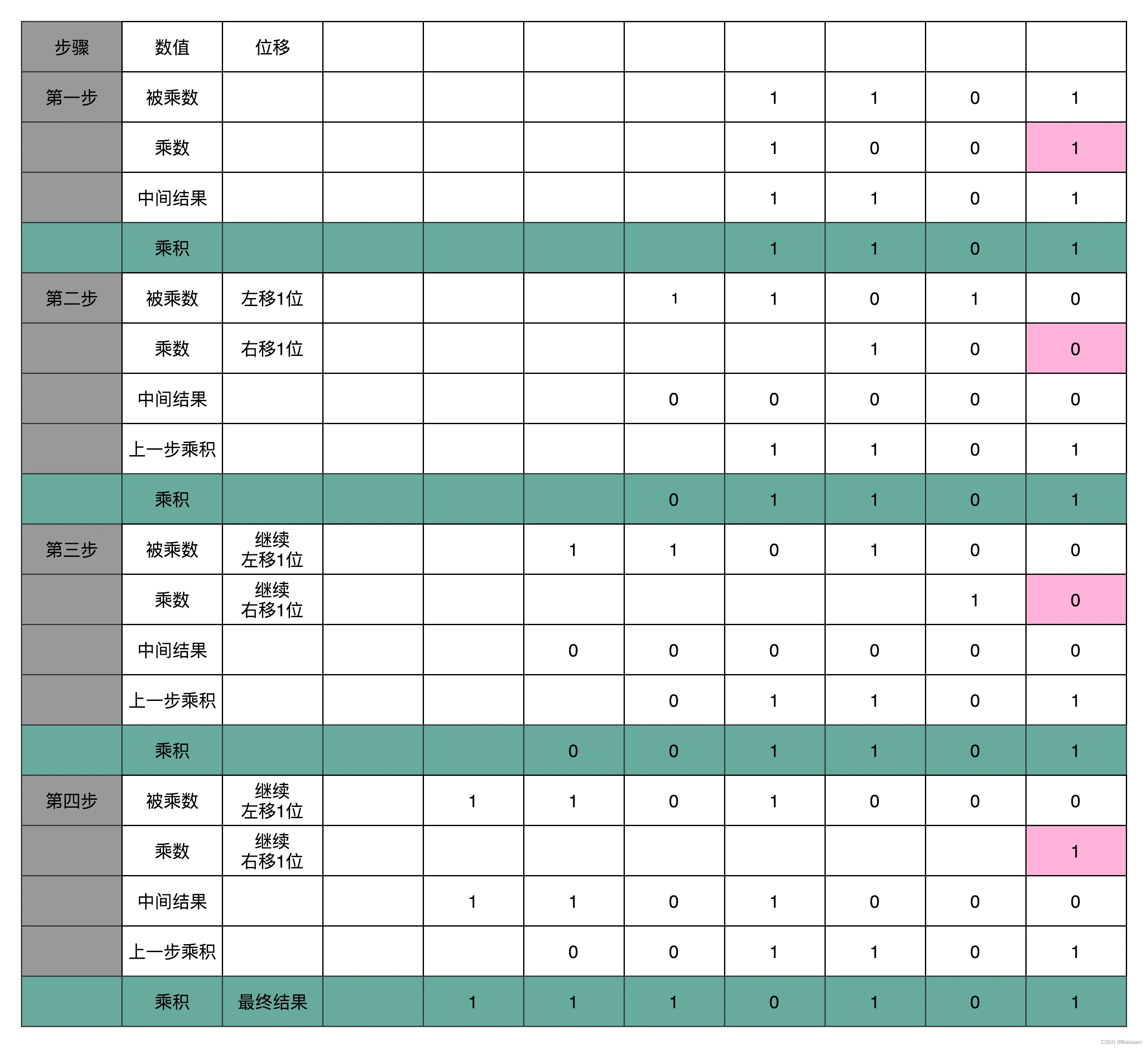
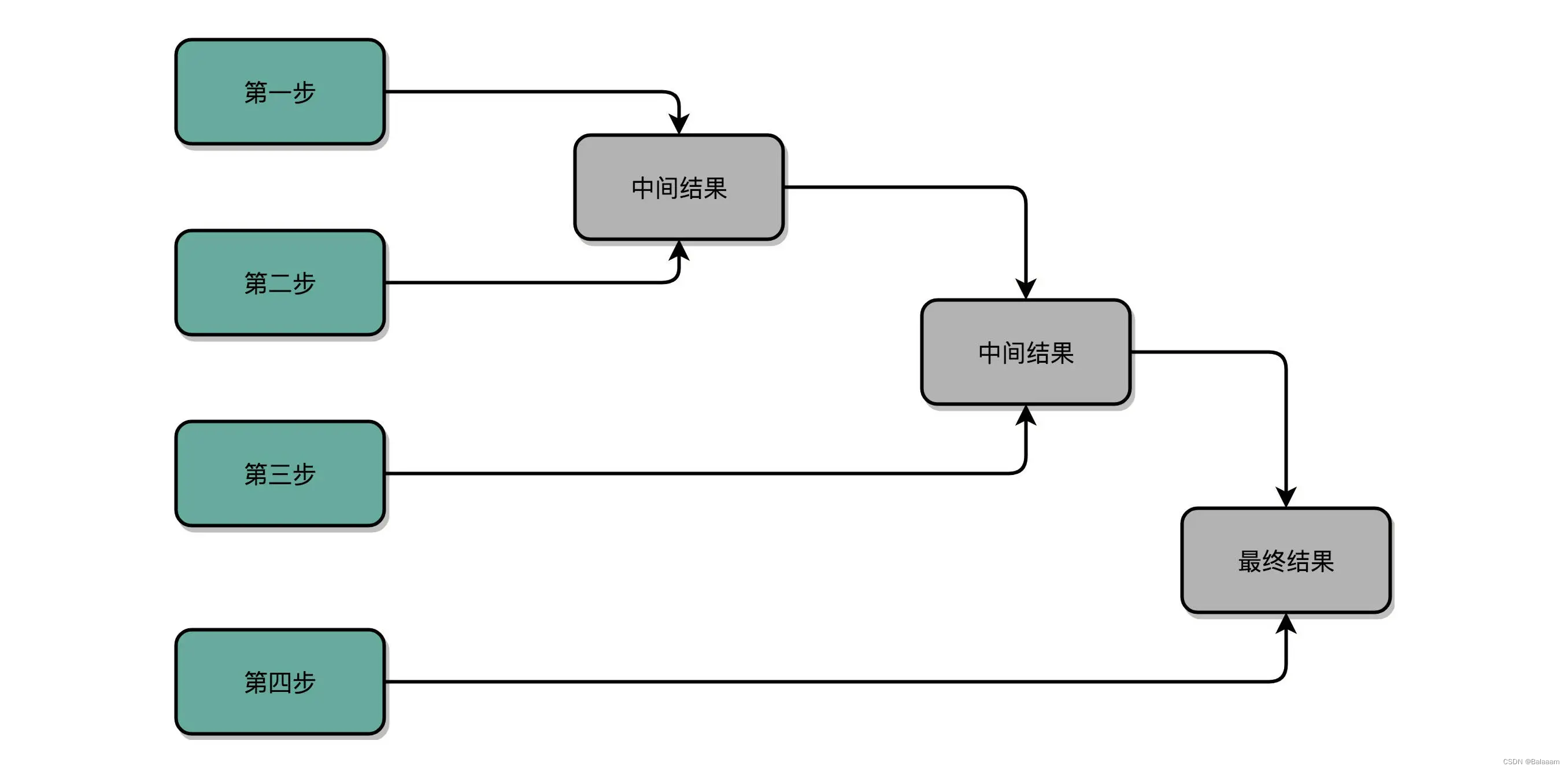
在这个乘法器本质上就是把乘法展开，变成了“加法 + 移位”来实现。如果是 4 位数，要进行分 4 组“位移 + 加法”的操作。

而且这 4 组操作不能同时进行。下一组的加法要依赖上一组的加法后的计算结果，下一组的位移也要依赖上一组的位移的结果。这样，整个算法是“顺序”的，每一组加法或者位移的运算都需要一定的时间。

最终这个乘法的计算速度，和我们要计算的数的位数有关。即，这样的一个顺序乘法器进行计算的时间复杂度是 $O(N)$。$N$：乘法的数里面的位数。

2. 并行加速方法

通过改造电路，可以将 $O(N)$ 降为 $O(\log N)$。32 位数虽然是 32 位加法，但是可以让很多加法同时进行。32 位整数的乘法，其实就变成了 32 个数相加。

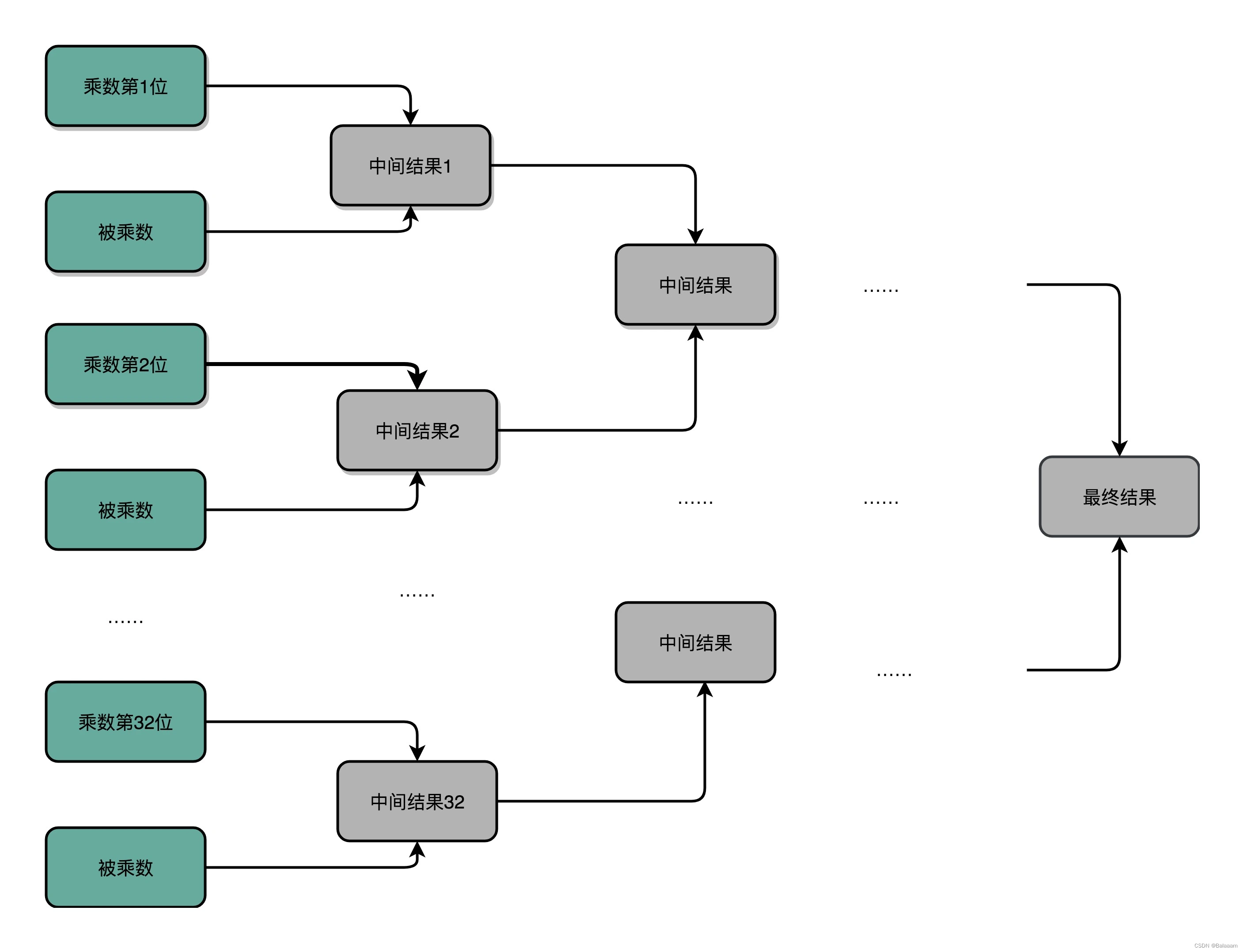
对应 CPU 的硬件上，就是需要更多的晶体管开关来放下中间结果。

3. 电路并行

电路并行主要用来降低 门延迟（Gate Dalay）。每一个全加器，都要等待上一个全加器，把对应的进入输入结果算出来，才能算下一位的输出。位数越多，越往高位走，等待前面的步骤就越多，这个等待的时间就是 门延迟。

除了门延迟之外，还有一个问题就是时钟频率。在上面的顺序乘法计算里面，如果我们想要用更少的电路，计算的中间结果需要保存在寄存器里面，然后等待下一个时钟周期的到来，控制测试信号才能进行下一次移位和加法。

我们通过电路并行来优化加法器。

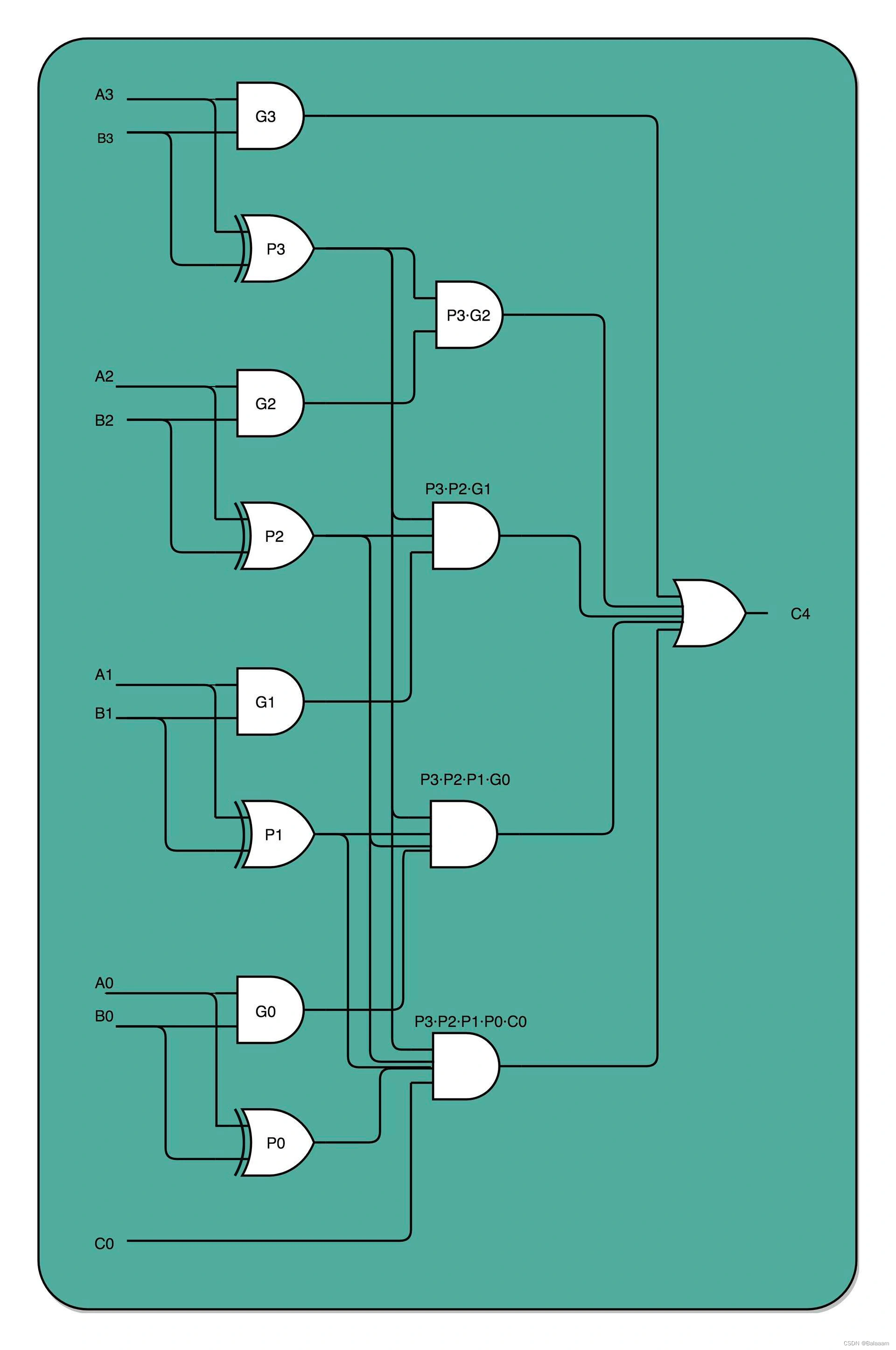
如果我们完全展开电路，高位的进位和计算结果，可以和低位的计算结果同时获得。这个的核心原因是电路是天然并行的，一个输入信号，可以同时传播到所有接通的线路当中。

参考

极客时间《深入浅出计算机组成原理》：http://gk.link/a/11UMi