当前位置： 首页 > news >正文

LeetCode热题100JS（49/100）第九天|199|114|105|437|236

news 来源：原创 2025/5/14 9:17:21

 199. 二叉树的右视图

题目链接：199. 二叉树的右视图

难度：中等

刷题状态：2刷

新知识：

解题过程

思考

示例 1：

输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

放下1刷过程在题解

题解分析

参考题解链接：【视频】如何灵活运用递归？（Python/Java/C++/Go/JS/Rust）

详细分析如下

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */

var rightSideView = function(root) {
    if(!root){
        return []
    }
    let res=[]
    function rightDepth(node,depth){
        if(!node){
            return 
        }
        if(depth==res.length){
            res.push(node.val)
        }
        rightDepth(node.right,depth+1)
        rightDepth(node.left,depth+1)
    }
    rightDepth(root,0)
    return res
};

手搓答案（无非废话版）

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */

var rightSideView = function(root) {
    let res=[]
    function dfs(node,depth){
        if(!node) return 
        if(res.length==depth) res.push(node.val)
        dfs(node.right,depth+1)
        dfs(node.left,depth+1)
    }
    dfs(root,0)
    return res
};

总结

 可以用res.length==depth来判断是否传入数据，注意right要先递归，这样才是传入右边的数据

 114. 二叉树展开为链表

题目链接：​​​​​​​​​​​​​​114. 二叉树展开为链表

难度：中等

刷题状态：1刷

新知识：

解题过程

思考

示例 1：

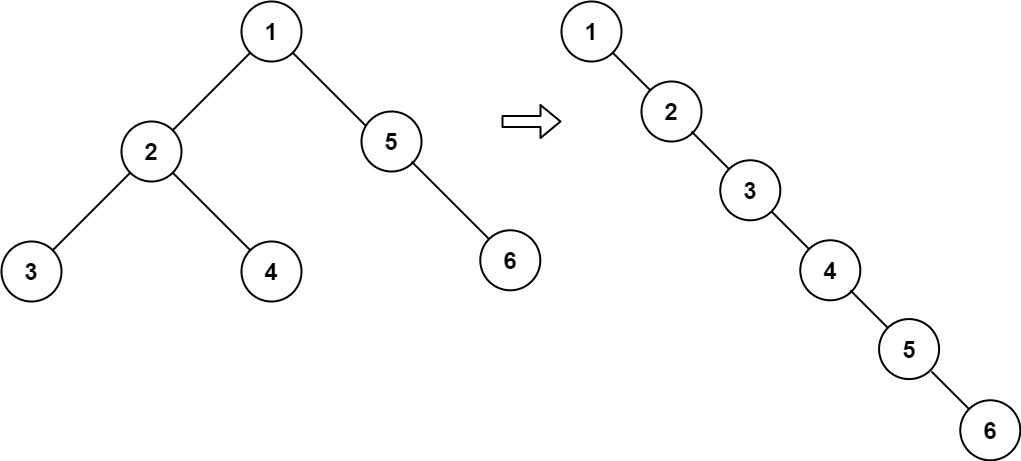
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]
题解分析

参考题解链接：​​​​​​​详细通俗的思路分析，多解法​​​​​​​

详细分析如下


/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
    let pre=null
    function dfs(node){
        if(!node) return 
        首先递归地遍历当前节点的右子树。由于目标是构建右斜树，所以先处理右子树有助于保持相对顺序。
        dfs(node.right)
        dfs(node.left)
        //将当前节点的右子节点设置为 pre，即前一个节点。这一步是构建右斜树的关键，它将当前节点的左子树之前的所有节点链接起来。
        node.right=pre
        //更新 pre 为当前节点。这样，在下一次迭代中，当前节点将成为下一个节点的“前一个节点”。
        pre=node
        node.left=null
    }
    dfs(root)
};

手搓答案（无非废话版）

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
    let pre=null
    function dfs(node){
        if(!node) return 
        dfs(node.right)
        dfs(node.left)
        node.right=pre
        pre=node
        node.left=null
    }
    dfs(root)
};

总结

 可以用res.length==depth来判断是否传入数据，注意right要先递归，这样才是传入右边的数据

 ​​​​​​​​​​​​​​105. 从前序与中序遍历序列构造二叉树

题目链接：​​​​​​​​​​​​​​​​​​​​​​​​​​​​105. 从前序与中序遍历序列构造二叉树

难度：中等

刷题状态：2刷

新知识：

解题过程

思考

示例 1:

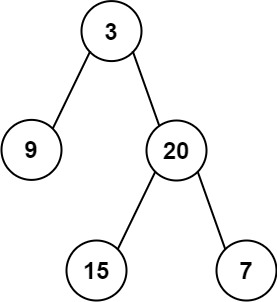
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

放下1刷过程在题解

题解分析

参考题解链接：​​​​​​​详细通俗的思路分析，多解法​​​​​​​

详细分析如下

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    let dic={}
    for(let i=0;i<inorder.length;i++){
        dic[inorder[i]]=i
    }
    //开始递归
    function dfs(pre,left,right){
        if(left>right) return null
        //创建根节点
        let node=new TreeNode(preorder[pre])
        //搜索preorder元素（根节点）在inorder中的索引
        let i=dic[preorder[pre]]
        //创建左子树
        node.left=dfs(pre+1,left,i-1)
        //创建右子树
        node.right=dfs(pre+1+i-left,i+1,right)
        return node
    }
    return dfs(0,0,inorder.length-1)
};

手搓答案（无非废话版）

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    let dic={}
    for(let i=0;i<inorder.length;i++){
        dic[inorder[i]]=i
    }
    function dfs(pre,left,right){
        if(left>right) return null
        let node=new TreeNode(preorder[pre])
        let i=dic[preorder[pre]]
        node.left=dfs(pre+1,left,i-1)
        node.right=dfs(pre+1+i-left,i+1,right)
        return node
    }
    return dfs(0,0,inorder.length-1)
};

总结

 重点理解这两行

        node.left=dfs(pre+1,left,i-1)

        node.right=dfs(pre+1+i-left,i+1,right)

  1. pre+1:
    • 前序遍历中，pre 是当前子树根节点的索引。
    • pre+1 是左子树根节点在前序遍历数组中的索引，因为前序遍历紧接着根节点访问左子树。
  2. left 到 i-1:
    • left 是当前子树在中序遍历中的起始索引。
    • i 是根节点在中序遍历中的位置。
    • i-1 是左子树在中序遍历中的结束索引。

因此，这一行代码通过递归调用 dfs 构建当前节点的左子树。

  1. pre+1+i-left:
    • pre+1 是左子树根节点在前序遍历中的起始索引。
    • i-left 是左子树中的节点数。
    • 因此，pre+1+i-left 是右子树根节点在前序遍历中的起始索引。
  2. i+1 到 right:
    • i+1 是右子树在中序遍历中的起始索引。
    • right 是当前子树在中序遍历中的结束索引。

这一行代码通过递归调用 dfs 构建当前节点的右子树。

 ​​​​​​​437. 路径总和 III

题目链接：​​​​​​​437. 路径总和 III

难度：中等

刷题状态：1刷

新知识：

解题过程

思考

示例 1：

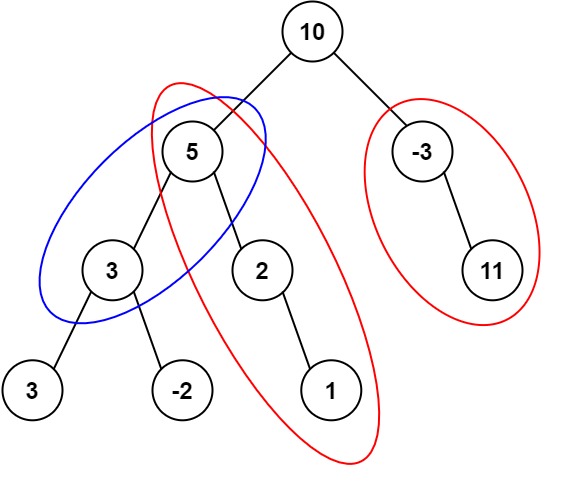
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
题解分析

参考题解链接：【视频】如何灵活运用递归？（Python/Java/C++/Go/JS/Rust）

详细分析如下

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
    let res=0
    //用于记录遍历过程中遇到的前缀和及其出现的次数
    let cnt=new Map()
    //节点和为0的情况有1种
    cnt.set(0,1)
    //s记录当前路径上的节点之和
    function dfs(node,s){
        if(!node) return null
        s+=node.val
        // console.log(s-targetSum,cnt)
        if(cnt.get(s-targetSum)){
            //如果有，说明某个祖先节点到当前节点的路径和等于 targetSum
            res+=cnt.get(s-targetSum)
        }
        if(!cnt.get(s)) cnt.set(s,0)
        cnt.set(s,cnt.get(s)+1)

        dfs(node.left,s)
        dfs(node.right,s)
        //复位
        cnt.set(s,cnt.get(s)-1)
    }
    dfs(root,0)
    return res
};

手搓答案（无非废话版）

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
    let cnt =new Map(),res=0
    cnt.set(0,1)
    function dfs(node,s){
        if(!node) return null
        s+=node.val
        if(cnt.get(s-targetSum)){
            res+=cnt.get(s-targetSum)
        }
        if(!cnt.get(s)) cnt.set(s,0)
        cnt.set(s,cnt.get(s)+1)
        dfs(node.left,s)
        dfs(node.right,s)
        cnt.set(s,cnt.get(s)-1)
    }
    dfs(root,0)
    return res
};

总结

 注意要先设置（0，1）的初值

 ​​​​​​​236. 二叉树的最近公共祖先

题目链接：​​​​​​​​​​​​​​236. 二叉树的最近公共祖先

难度：中等

刷题状态：2刷

新知识：

解题过程

思考

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

放下1刷过程在题解

题解分析

参考题解链接：【视频】如何灵活运用递归？（Python/Java/C++/Go/JS/Rust）

详细分析如下

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    if(!root||root==p||root==q) return root
    //递归地在当前节点的左子树中查找p和q的最低公共祖先，并将结果存储在left变量中。
    let left=lowestCommonAncestor(root.left,p,q)
    //递归地在当前节点的右子树中查找p和q的最低公共祖先，并将结果存储在right变量中。
    let right=lowestCommonAncestor(root.right,p,q)

    //这意味着p和q的最低公共祖先在右子树中，或者p和q中的一个就是right节点本身。
    if(!left) return right
    //这意味着p和q的最低公共祖先在左子树中，或者p和q中的一个就是left节点本身。
    if(!right) return left

    //如果left和right都不为null，说明p和q分别位于当前节点的左右两侧（或者其中一个就是当前节点）。在这种情况下，返回当前节点作为p和q的最低公共祖先。
   
    return root
    //return left && right ? root : left || right;
};

手搓答案（无非废话版）

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    if(!root||root==p||root==q) return root
    let left=lowestCommonAncestor(root.left,p,q)
    let right=lowestCommonAncestor(root.right,p,q)
    if(!left) return right
    if(!right) return left
    return root
};

总结

 重点理解

    if(!left) return right

    if(!right) return left

这两个逻辑

相关文章：

  • undo log ，redo log 和binlog的区别？
  • 使用 yum 命令安装 MariaDB 指南
  • 安卓edge://inspect 和 chrome://inspect调试移动设备上的网页
  • 瑞幸需要宇树科技
  • UNION，UNION ALL 的详细用法
  • 【leetcode hot 100 437】路径总和Ⅲ
  • Typora 使用教程(标题,段落,字体,列表,区块,代码,脚注,插入图片,表格,目录)
  • 什么是广播系统语言传输指数 STIPA
  • CCF CSP 第30次（2023.05）（1_仓库规划_C++）
  • 关于运行 npm run serve/dev 运行不起来，node_modules Git忽略不了等(问题)
  • 冰羚杂谈（四）上下游对齐工作节奏
  • 基于SpringBoot+Vue3实现的宠物领养管理平台功能一
  • 算法竞赛-基础算法-位运算
  • 基于cat1的多传感器融合的贵重资产管理解决方案项目说明书
  • 基于Django的交通指示图像识别分析系统
  • Unity WebGL IIS报错无法使用
  • LeetCode 解题思路 19（Hot 100）
  • 轨迹规划：基于查找的(search-based)路径规划算法
  • Python集合
  • 如何使用MySQL快速定位慢SQL问题？企业级开发中常见业务场景中实际发生的例子。（一）
  • 马上评丨火车穿村而过多人被撞身亡，亡羊补牢慢不得
  • 小米SU7 Ultra风波升级：数百名车主要求退车，车主喊话雷军“保持真诚”
  • 石家庄推动城市能级与民生福祉并进
  • 中方发布会：中美经贸高层会谈氛围是坦诚的、深入的、具有建设性的
  • 普京：俄中关系是国家间关系的真正典范
  • 三大股份制银行入局AIC，一级市场再迎“活水”