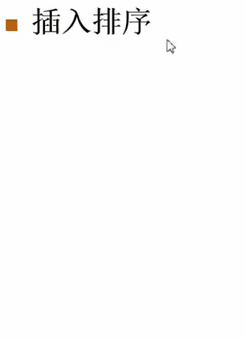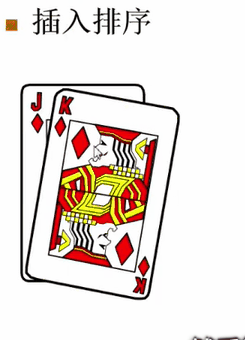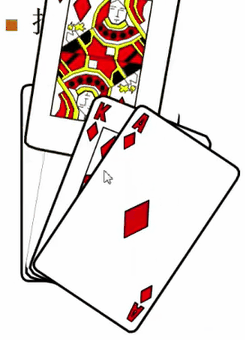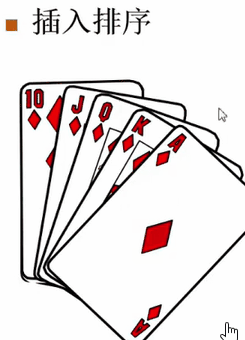第九讲 排序(上)
9.1 简单排序

![]()
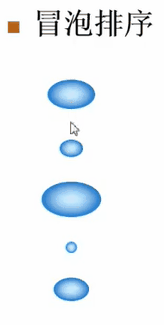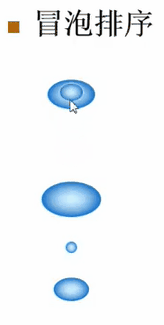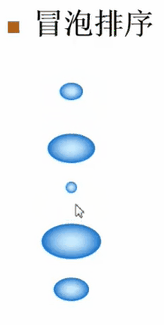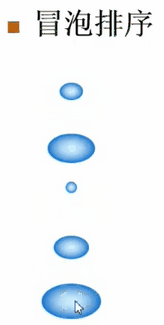
假设有这么一堆的泡泡,现在要把最小的泡泡排在最上面,最大的泡泡排在最下面。
流程:
每次从上到下比较两个相邻的泡泡,如果他们的顺序是对的(即小的在上面、大的在下面),那就不动了。如果顺序是错的,就把这两个泡泡的顺序换一下,然后接着往下走。这样一直走到最后一个泡泡,就完成了一趟排序。然后不管前面泡泡的状况是什么样子,可以肯定:最大的泡泡一定已经放到最下面。最大的泡泡的位置已经确认了,接下去在做第二趟排序时,仍从上到下重复这个过程,但是只需对前面的n-1个泡泡重复这个过程即可
//冒泡排序
typedef int ElementType;
void Bubble_Sort(ElementType A[], int N)
{
int flag;
//控制循环次数,每次要遍历的泡泡依次少一个
for (int P = N - 1; P >= 0; P--) {
flag = 0; //标记是否发生了交换
for (int i = 0; i < P; i++) { /* 一趟冒泡 */
if (A[i] > A[i + 1]) {
int tmp = A[i]; //交换相邻元素
A[i] = A[i+1];
A[i+1] = tmp;
flag = 1; /* 标识发生了交换 */
}
}
if (flag == 0) break; /* 全程无交换,直接跳出,已经有序 */
}
}
算法复杂度:
最好情况:顺序(这个序列已经是顺序的,只需要遍历一遍就行了) T = O(N)
最坏情况:逆序(全部逆序,严格执行n-1次排序) T = O()
冒泡排序的优缺点:
优点:冒泡排序每次从上到下按一个方向扫描,而且每次交换相邻的两个元素,该操作对于数组和链表没有问题。在比较两个元素大小时,只有当前面元素严格大于下一个元素时才做交换,如果两个是相等的话不做交换,这也就保证了这个排序算法的稳定性
缺点:算法复杂度较高,一个O()数量级的排序算法往往是不可接受的
![]()
插入排序可以理解为怎么抓一手牌。
第一张牌摸进来是J。
第二张牌摸进来是K。K比J大,把K放在J的后面。
第三张牌摸进来是A。A比K大,把A放在K的后面。不用让A去与J比,因为K已经比J大了。
第四张牌摸进来是Q。Q比A小,所以它应该排在A前面,于是A这张牌要往后错一位。它又比K小,所以K也往后错一位。然后发现它比J要大,J不用错位了,Q插进去,这个空位就是它的。
第五章牌摸进来是10。把这个四张牌全部一个一个向后错位,然后把最前面这个位置空出来给10。
//插入排序
typedef int ElementType;
void Insertion_Sort(ElementType A[], int N)
{
int Tmp;
int i;
//从1开始,默认我们有第一张牌
for (int P = 1; P < N; P++) {
Tmp = A[P]; /* 摸下一张牌 */
for (i = P; i > 0 && A[i - 1] > Tmp; i--)
A[i] = A[i - 1]; /* 移出空位 */
A[i] = Tmp; /* 新牌落位 */
}
}
算法复杂度:
最好情况:顺序(这个序列已经是顺序的,只需要遍历一遍就行了) T = O(N)
最坏情况:逆序(全部逆序,先摸到A,再摸到 K、Q、J、10,每次都要把后面的牌往后挪) T = O()
例子:
给定初始序列{34, 8, 64, 51, 32, 21},冒泡排序和插入排序分别需要多少次元素交换才能完成?
冒泡排序需要9次元素交换,插入排序也需要9次交换。它们两个交换的次数是刚刚好碰巧了一样吗?

无论如何它都要把整个元素从头到尾扫描一遍,所以至少是O(N)复杂度。另外操作的次数跟逆序对的个数成正比,所以实际上是O(N+I)的复杂度。如果这个序列里的I(逆序对个数)非常少(比如跟N是同一个数量级的),即序列基本有序的话,那么插入排序算法的时间复杂度是线性,是O(N)这个数量级的,是一种非常快的排序算法

9.2 希尔排序
示例:
这里有个数组
Shell sort的第一步要先做一个5间隔的排序(这个序列每隔5个来选取元素构成子序列),这里得到子序列(81,35,41)
对这个子序列做插入排序,然后将其放在对应的位置
接着继续做一个5间隔的排序,这里得到序列(94,17,75)
对这个子序列做插入排序,然后将其放在对应的位置
接着继续做5间隔的排序,子序列为(11,95,15)
接着继续做5间隔的排序,子序列为(96,28)
接着继续做5间隔的排序,子序列为(12,58)
此时调整间隔,在5间隔排序的结果基础上开始做3间隔排序。
开始做第一次3间隔排序
开始做第二次3间隔排序
开始做第三次3间隔排序
最后在3间隔排序的结果基础上做1间隔排序


//希尔排序
void Shell_sort(int A[], int N)
{
int Tmp, i;
for (int D = N / 2; D > 0; D /= 2) { /* 希尔增量序列 */
for (int P = D; P < N; P++) { /* 插入排序 */
Tmp = A[P];
for (i = P; i >= D && A[i - D] > Tmp; i -= D)
A[i] = A[i - D];
A[i] = Tmp;
}
}
}
最坏情况下,希尔排序的时间复杂度是 θ (
)
注意:这里是 θ,代表既是上界也是下界,说明复杂度实际上会达到
这个数量级。而其他排序是 O,代表上界,即最坏情况下才会使这么大。
示例:
有以下数组,共16个元素,先做一次8-间隔排序,发现元素顺序没改变
在8-间隔排序结果基础上做4-间隔排序,发现顺序还是没变
在4-间隔排序结果基础上做2-间隔排序,发现顺序还是没变
最后还是靠1间隔排序才得到最终结果
原因分析:增量元素不互质(8是4的倍数,4是2的倍数),则小增量可能根本不起作用。

//希尔排序-用Sedgewick增量
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
void ShellSort(int A[], int N)
{ /* 希尔排序 - 用Sedgewick增量序列 */
int Si, D, P, i;
int Tmp;
/* 这里只列出一小部分增量 */
int Sedgewick[] = { 929, 505, 209, 109, 41, 19, 5, 1, 0 };
/* 初始的增量Sedgewick[Si]不能超过待排序列长度 */
for (Si = 0; Sedgewick[Si] >= N; Si++);
for (D = Sedgewick[Si]; D > 0; D = Sedgewick[++Si]) {
for (P = D; P < N; P++) { /* 插入排序*/
Tmp = A[P];
for (i = P; i >= D && A[i - D] > Tmp; i -= D)
A[i] = A[i - D];
A[i] = Tmp;
}
}
}
int main(void)
{
int a;
int A[30];
//为数组A分配30个随机值
srand((unsigned)time(NULL));
for (int i = 0; i < 30; i++) {
a = rand();
A[i] = a;
}
printf("希尔排序前:\n");
for (int i = 0; i < 30; i++)
printf("%d ", A[i]);
ShellSort(A, 30);
printf("\n希尔排序后:\n");
for(int i = 0; i < 30; i++)
printf("%d ", A[i]);
return 0;
}
9.3 堆排序

每次从A[i]到A[N-1]这一段(未排序的部分)里去找一个最小元,把最小元的位置赋给一个变量MinPosition。然后把找到的最小元与有序部分(A[0]到A[i-1])后面一位上的元素(A[i])互换。
问题:
①在交换这两个元素时,大多数情况下它们不是挨着的,可能跳了很远的距离做一个交换。可能这一次交换能消掉很多的逆序对。但最坏情况下每次找到一个最小元都必须换一下,循环了多少N-1次
②瓶颈在ScanForMin这个函数。要从A[i]到A[N-1]里面找最小元,选择排序是一个简单粗暴的方法,即从A[i]一直扫描到A[N-1],然后把最小元挑出来,因此ScanForMin也是for循环。
③整个算法相当于外头套了一层for循环,里面也是一层for循环。无论如何选择排序的时间复杂度都是Θ()这个数量级的,无所谓最好情况还是最坏情况。
想要得到一个更快的算法,关键是如何把找到最小元这一步变快。看见最小元想到一个很有用的工具:最小堆。最小堆的特点:它的根结点一定存的是最小元

![]()
没有必要做单独开辟一片空间,并在最后做元素复制。如何把这一步跳过去呢?
示例:
有一个四个元素(a b c d)的数组,大小关系为a<b<c<d
先将其调整成一个最大堆
由于在一个排好序的数组里,最大元素应该放在最后一个位置。所以把根结点跟最后一个结点做一个交换,把b放上去,把d放下来
放下来以后,就把这整个堆的规模-1,把这个d排除在外。因为后面再做什么,这个d都不用动了,它已经放在最终正确的位置上了
剩下这个堆还有三个元素,然后继续把这个堆调整成一个最大堆
然后重复前面的步骤,把c换到最后的位置上去
然后把c排除掉
剩下这个堆还有2个元素,继续把这个堆调整成一个最大堆
重复前面的步骤,把根结点b换到最后的位置上去
最后完成了排序
注意:
堆的元素是从第一个下标为1的元素开始计数的,A[0]不放任何真的元素,里面放的是一个哨兵。但是在排序算法里,用户是从第0个元素就开始存的。所以堆排序里堆的元素是从0开始记的,这也导致任何一个结点跟它孩子结点的下标的关系就不一样了:
根结点下标为i,左孩子下标为2i+1,右孩子下标为2i+2
//堆排序
void Heap_Sort ( ElementType A[], int N )
{
for ( i=N/2-1; i>=0; i-- )/* BuildHeap */
PercDown( A, i, N );
for ( i=N-1; i>0; i-- ) {
Swap( &A[0], &A[i] ); /* DeleteMax */
PercDown( A, 0, i );
}
}

//堆排序完整代码
void Swap( ElementType *a, ElementType *b )
{
ElementType t = *a; *a = *b; *b = t;
}
void PercDown( ElementType A[], int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p ) */
/* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X;
X = A[p]; /* 取出根结点存放的值 */
for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
Child = Parent * 2 + 1;
if( (Child!=N-1) && (A[Child]<A[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= A[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
A[Parent] = A[Child];
}
A[Parent] = X;
}
void HeapSort( ElementType A[], int N )
{ /* 堆排序 */
int i;
for ( i=N/2-1; i>=0; i-- )/* 建立最大堆 */
PercDown( A, i, N );
for ( i=N-1; i>0; i-- ) {
/* 删除最大堆顶 */
Swap( &A[0], &A[i] ); /* 见代码7.1 */
PercDown( A, 0, i );
}
}
9.4 归并排序

示例:
有两个子序列,这两个子序列本身已经排好序。目标是开另外一个数组,把这些数字一个一个放到这个数组里去,并且希望最后这个数组是从小到大有序的
跟之前两个多项式相加的想法相似:先准备好三个指针,A指针指向A序列当前第一个元素;B指针指向B序列当前第一个元素;C指针指向现在要放的这个元素的位置
第一次比较,1更小,放入新数组中,并将A指针和C指针向后移动1位
继续比较,2更小,放入新数组中,并将B指针和C指针向后移动1位
接下来就一直重复即可……

/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置 */
void Merge( ElementType A[], ElementType TmpA[],
int L, int R, int RightEnd )
{
LeftEnd = R - 1; /* 左边终点位置。假设左右两列挨着 */
Tmp = L; /* 存放结果的数组的初始位置 */
NumElements = RightEnd - L + 1;
while( L <= LeftEnd && R <= RightEnd ) {
if ( A[L] <= A[R] ) TmpA[Tmp++] = A[L++];
else TmpA[Tmp++] = A[R++];
}
while( L <= LeftEnd ) /* 直接复制左边剩下的 */
TmpA[Tmp++] = A[L++];
while( R <= RightEnd ) /*直接复制右边剩下的 */
TmpA[Tmp++] = A[R++];
//从后往前导
for( i = 0; i < NumElements; i++, RightEnd -- )
A[RightEnd] = TmpA[RightEnd];
}

分而治之:假设待排的序列放在一个数组里,把它一分为二,然后递归地把左边排好序,再递归地把右边排好序。这样就得到两个有序的子序列,而且它们肩并肩放在一起,最后调用上面写的归并算法把这两个有序的子序列归并成最终的有序序列。
void MSort( ElementType A[], ElementType TmpA[],
int L, int RightEnd )
{
int Center;
if ( L < RightEnd ) {
Center = ( L + RightEnd ) / 2; //中间位置
MSort( A, TmpA, L, Center ); //递归处理左边
MSort( A, TmpA, Center+1, RightEnd ); //递归处理右边
Merge( A, TmpA, L, Center+1, RightEnd ); //归并两个有序序列
}
}
算法复杂度:
假设解决整个问题用的时间是T(N),那么递归地解决左半边用的时间一定是 T(N/2),因为数据的规模减了一半。递归地解决右半边用的时间也是 T(N/2)。然后还需执行一步Merge规并,这一步的时间复杂度为 O(N) 数量级。
T(N) = T(N/2) + T(N/2) + O(N)T(N) = O(NlogN)此处的NlogN是非常强的NlogN,它没有最好时间复杂度,也没有最坏时间复杂度,也没有平均时间复杂度,任何情况下它都是 O(NlogN)

有一个约定:任何排序算法都要有一个统一的接口,传进来的参数只能是原始的数组A加上数组里面元素的个数N。所以之前的MSort函数不满足这个条件,必须要给用户一个友好的统一的函数接口。

令人疑惑的地方:为什么MSort要一直带着TmpA呢?程序执行过程中,真正用到TmpA是在Merge函数里面,为什么不直接在Merge函数的内部去声明TmpA呢?
①如果在Merge_sort里面刚进去时就声明了另外一个等长的数组TmpA,然后进入了MSort,把这个问题一分为二,开始递归地解决这个问题。在递归过程中,从始至终都是在同一个数组的某一段上面反反复复做Merge操作。从头到尾malloc只调用了一次,程序执行完后free也只执行了一次。
②如果只在Merge中间声明一个临时数组,在这个递归程序里要反复地malloc、反复地free,这样做很不划算。
//归并排序 - 递归实现
/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
int LeftEnd, NumElements, Tmp;
int i;
LeftEnd = R - 1; /* 左边终点位置 */
Tmp = L; /* 有序序列的起始位置 */
NumElements = RightEnd - L + 1;
while( L <= LeftEnd && R <= RightEnd ) {
if ( A[L] <= A[R] )
TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
else
TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
}
while( L <= LeftEnd )
TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
while( R <= RightEnd )
TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
for( i = 0; i < NumElements; i++, RightEnd -- )
A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}
void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{ /* 核心递归排序函数 */
int Center;
if ( L < RightEnd ) {
Center = (L+RightEnd) / 2;
Msort( A, TmpA, L, Center ); /* 递归解决左边 */
Msort( A, TmpA, Center+1, RightEnd ); /* 递归解决右边 */
Merge( A, TmpA, L, Center+1, RightEnd ); /* 合并两段有序序列 */
}
}
void MergeSort( ElementType A[], int N )
{ /* 归并排序 */
ElementType *TmpA;
TmpA = (ElementType *)malloc(N*sizeof(ElementType));
if ( TmpA != NULL ) {
Msort( A, TmpA, 0, N-1 );
free( TmpA );
}
else printf( "空间不足" );
}
![]()
示例:
开始时一共有n个有序的子序列,每一个子序列里都只含有一个元素
下一步把相邻的两个有序的子序列做一次规并,于是形成了若干个有序的子序列,每个子序列的长度就变成了2
然后继续规并两个相邻的子序列,又产生一系列有序的子序列,这些子序列的长度就变成了4
以此类推,一直到最后得到一个完整的有序序列
复杂度分析:
①算法过程非常容易理解,但需要的额外空间复杂度有点恐怖。上图中的深度是 logN,如果在每一层要开一个新的临时数组去存中间结果的话,那么额外空间复杂度为 NlogN。
②真的有必要这么做吗?用这个非递归的算法实现规并排序,能够做到最小的额外空间复杂度是 O(N)。实际上只要开一个临时数组就够了,第一次把A规并到临时数组里;第二次把临时数组里的东西归并回A里,然后再把A归并到临时数组里,然后再把临时数组导回到A。
//一趟归并:
void Merge_pass( ElementType A[], ElementType TmpA[], int N,
int length ) /* length = 当前有序子列的长度 */
{
//i左到N-2*length就行了,因为如果N是奇数,那么会剩一个元素归并不了,我们最后去处理这个尾巴
for ( i=0; i <= N–2*length; i += 2*length )
//这里我们使用Merge1这个名字,因为传统Merge把结果放到A里面,我们这里要把结果放到TmpA里面
Merge1( A, TmpA, i, i+length, i+2*length–1 );
if ( i+length < N ) /* 归并最后2个子列,处理尾巴 */
Merge1( A, TmpA, i, i+length, N–1);
else /* 最后只剩1个子列 */
//说明归并完了,往A导入即可
for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}

优点:
它的平均复杂度是 O(NlogN),最坏时间复杂度也是 O(NlogN),而且它还是稳定的。
缺点:
需要额外的空间,并且需要在两个数组之间来回复制元素。
用途:Merge_sort基本不被用于做内排序,在外排序时是一个非常有用的工具
//归并排序 - 循环实现
/* 这里Merge函数已经在递归版本中给出 */
/* length = 当前有序子列的长度*/
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
int i, j;
for ( i=0; i <= N-2*length; i += 2*length )
Merge( A, TmpA, i, i+length, i+2*length-1 );
if ( i+length < N ) /* 归并最后2个子列*/
Merge( A, TmpA, i, i+length, N-1);
else /* 最后只剩1个子列*/
for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}
void Merge_Sort( ElementType A[], int N )
{
int length;
ElementType *TmpA;
length = 1; /* 初始化子序列长度*/
TmpA = malloc( N * sizeof( ElementType ) );
if ( TmpA != NULL ) {
while( length < N ) {
Merge_pass( A, TmpA, N, length );
length *= 2;
Merge_pass( TmpA, A, N, length );
length *= 2;
}
free( TmpA );
}
else printf( "空间不足" );
}