数据结构——排序
排序
1. 排序相关概念
将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序(递增/递减)的序列称为排序
设n个记录的序列为{R1,R2,…,Rn},其相应关键字序列为{K1,K2,…,Kn},这些关键字相互之间可以进行比较,即在它们之间存在着一种排序P1,P2,…,Pn,使其相应的关键字满足递增(升序),或递减(降序)的关系。
内排序
- 在排序过程中,所有排序记录调到内存中进行的排序,整个排序过程不需要访问外存
- 内排序是排序的基础
- 内存速度快,比较过程主导性能,内排序效率主要用比较次数和移动次数来衡量
外排序
- 排序过程中需对外存进行访问的排序
- 参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成
- 由于读写延迟是外存性能相关的主要问题,所以,外排序主要用读/写外存的次数作为衡量效率的指标
排序方法的稳定性
-
稳定的排序方法是若待排序的序列中,存在多个具有相同关键字的记录,经过排序,这些记录的相对次序保持不变,则称该算法是稳定的
原始序列:( 5, 3, 7, 2, 8, 10, 4, 7 )
排序结果:( 2, 3 ,4, 6, 7, 7, 8, 10 ) 是稳定的
排序结果:( 2, 3 ,4, 6, 7, 7, 8, 10 ) 是不稳定的
2. 插入排序
2.1 直接插入排序
插入排序类似于整理扑克牌。


以下图为例:
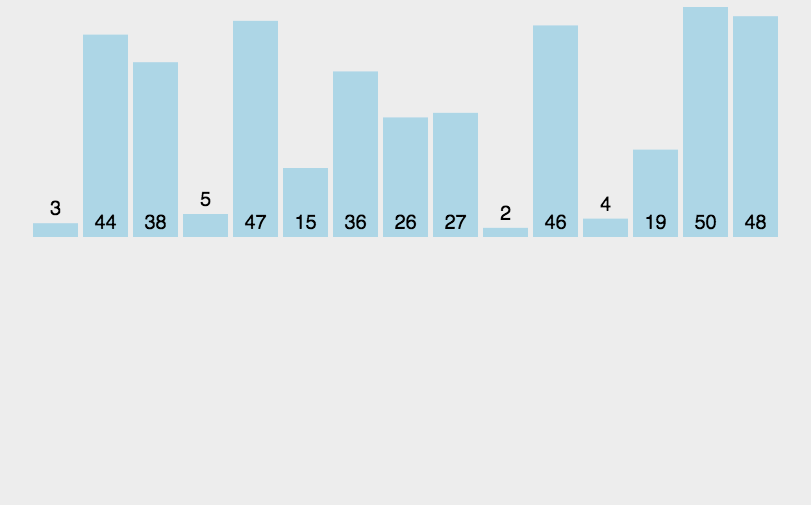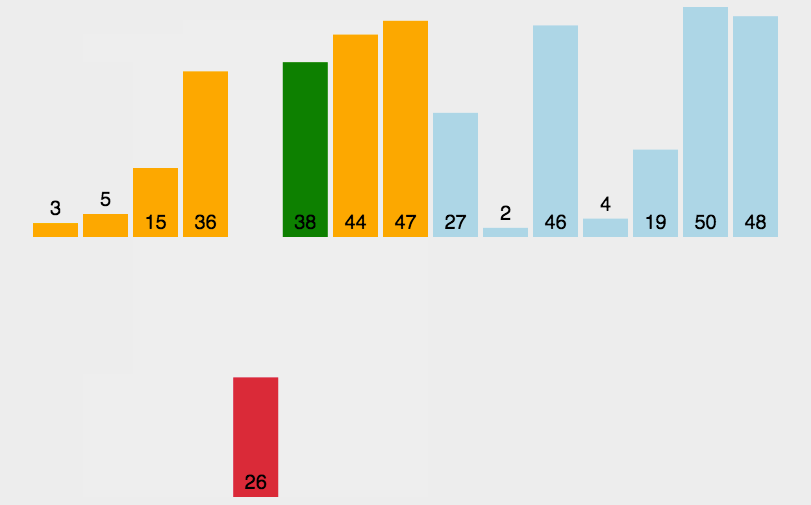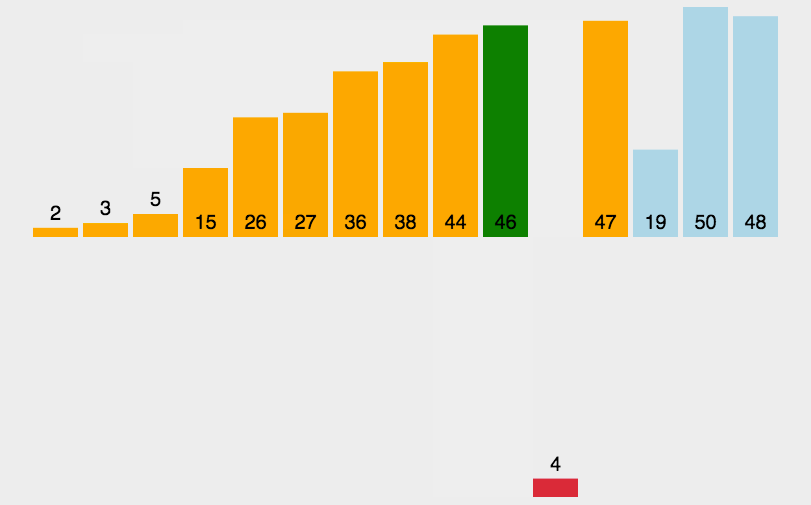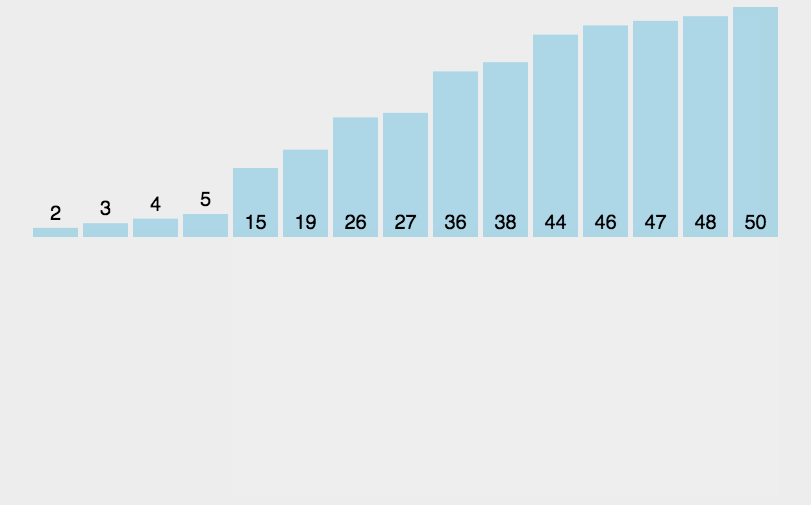

void InsertSort(int *a, int n)
{
for (int i = 1; i < n; i++)
{
int end = i - 1;
int temp = a[i];
while (end >= 0)
{
if (temp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = temp;
}
}
性能分析如下:
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:因为每次插入元素时总是从后往前先比较再移动,所以不会出现相同元素相对位置发生变化的情况,即直接插入排序是一个稳定的排序算法。
2.2 折半插入排序
折半插入排序就是使用前面提到的折半查找法,来找到需要插入元素的位置,原理很简单。确定插入位置后,再统一向后挪动元素。
void BInsertSort(SqList &L)
{
// 对顺序表L做折半插入排序
int i, j, low, high, m;
for (i = 2; i <= L.length; ++i)
{
L.r[0] = L.r[i]; // 将待插入的记录暂存到监视哨中
low = 1;
high = i - 1; // 置查找区间初值
while (low <= high) //折半查找法
{ // 在r[low..high]中折半查找插入的位置
m = (low + high) / 2; // 折半
if (L.r[0].key < L.r[m].key)
high = m - 1; // 插入点在前一子表
else
low = m + 1; // 插入点在后一子表
} // while
for (j = i - 1; j >= high + 1; --j)
L.r[j + 1] = L.r[j]; // 记录后移
L.r[high + 1] = L.r[0]; // 将r[0]即原r[i],插入到正确位置
} // for
}
从上述算法中,不难看出折半插入排序仅减少了比较元素的次数,时间复杂度约为 O ( n l o g n ) O(nlogn) O(nlogn)该比较次数与待排序表的初始状态无关,仅取决于表中的元素个数 n n n;而元素的移动次数并未改变它依赖于待排序表的初始状态。因此,折半插入排序的时间复杂度仍为 O ( n 2 ) O(n^2) O(n2),但对于数据量不很大的排序表,折半插入排序往往能表现出很好的性能。折半插入排序是一种稳定的排序算法。折半插入排序仅适用于顺序存储的线性表,比如数组等。
2.3 希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
如下图所示,第一趟增量取5,第二趟取增量取3,第三趟增量为1。

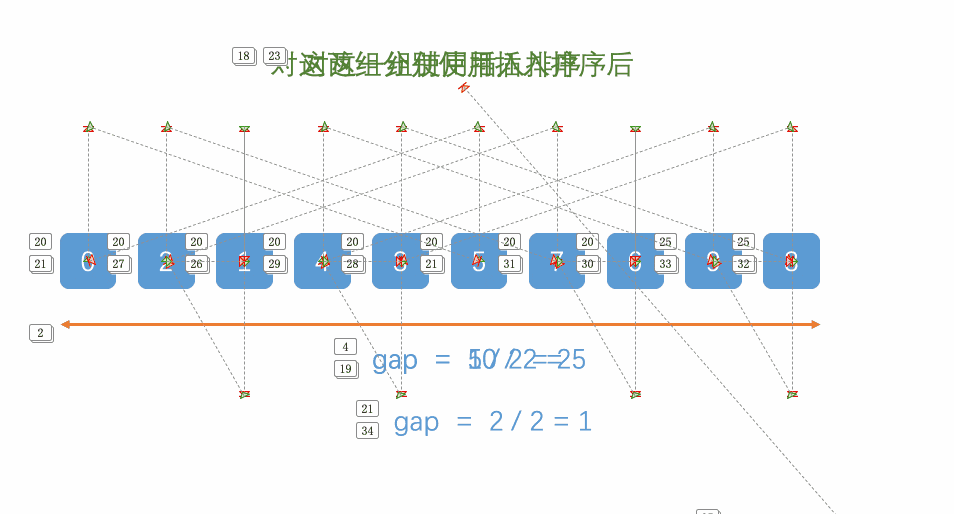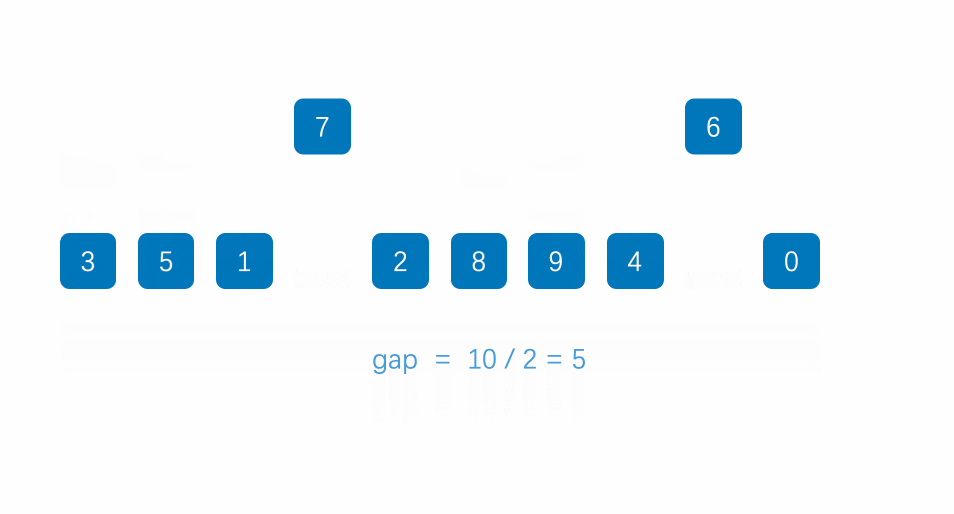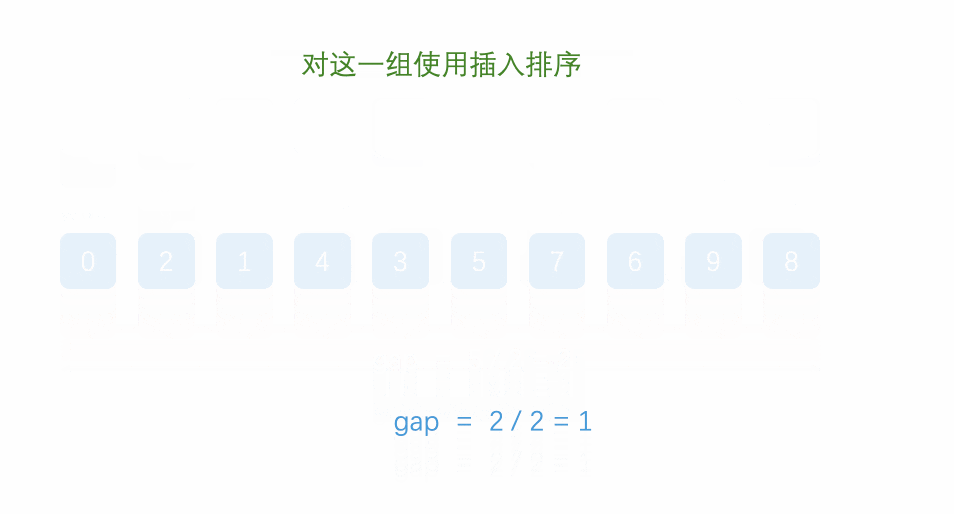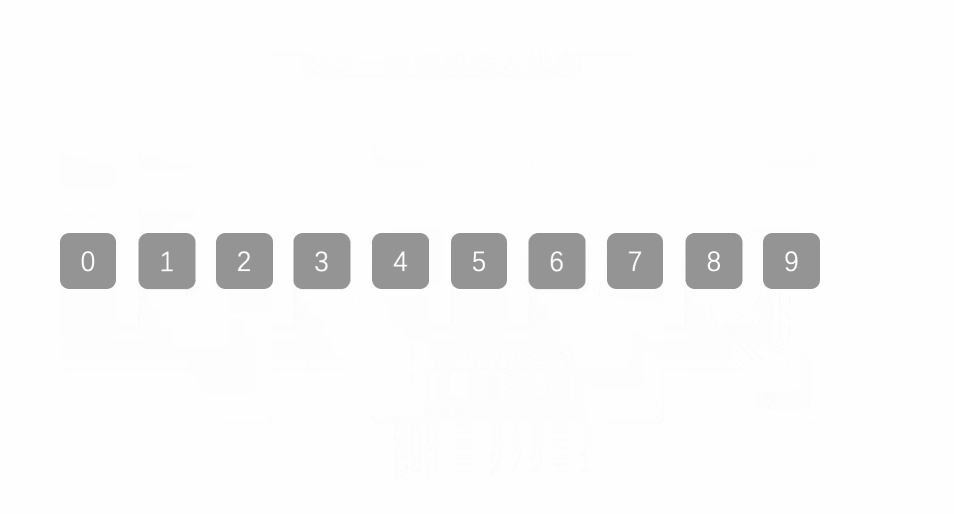
代码如下:
// 教材写法
void ShellInsert(SqList &L, int dk)
{
// 对顺序表L做一趟增量是dk的希尔插入排序
int i, j;
for (i = dk + 1; i <= L.length; ++i)
if (L.r[i].key < L.r[i - dk].key)
{ // 需将L.r[i]插入有序增量子表
L.r[0] = L.r[i]; // 暂存在L.r[0]
for (j = i - dk; j > 0 && L.r[0].key < L.r[j].key; j -= dk)
L.r[j + dk] = L.r[j]; // 记录后移,直到找到插入位置
L.r[j + dk] = L.r[0]; // 将r[0]即原r[i],插入到正确位置
} // for
}
// ShellInsert
void ShellSort(SqList &L, int dt[], int t)
{
// 按增量序列dt[0..t-1]对顺序表L作t趟希尔排序
int k;
for (k = 0; k < t; ++k)
ShellInsert(L, dt[k]); // 一趟增量为dt[t]的希尔插入排序
} // ShellSor
我更推荐下面这种写法,直观,便于理解。
template <class T>
void ShellSort(T *a, int n, int gap)
{
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
T temp = a[end + gap];
while (end >= 0)
{
if (temp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = temp;
}
}
}
性能分析如下:
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度:希尔排序的时间复杂度是尚未解决的难题,没有具体的值,以教材说法为主,主要与gap的值有关。


稳定性:不稳定,划分不同区间会改变相对次序。
3. 交换排序
3.1 冒泡排序
冒泡排序就不用多说了,典中典,刚开始学习C语言就接触到的排序算法。
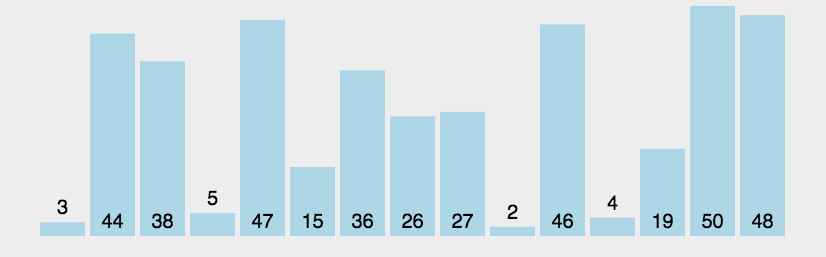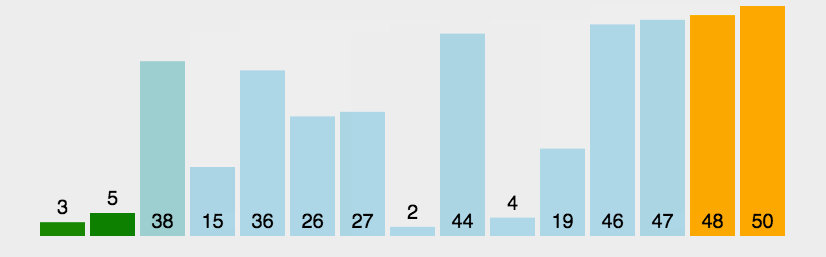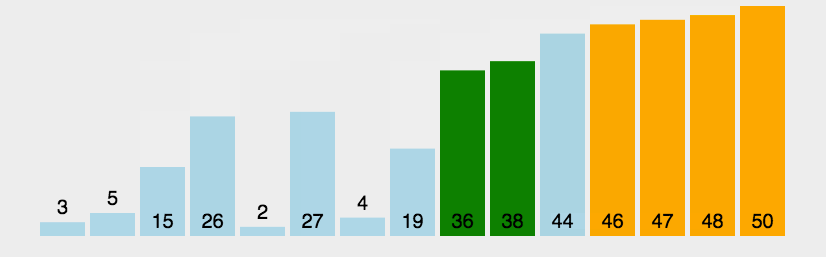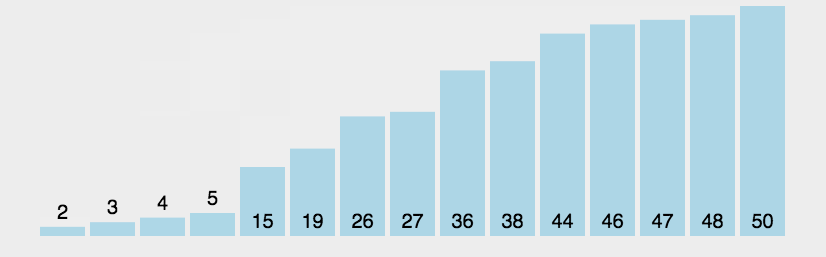
template <class T>
void BubbleSort(T *a, int n)
{
for (int i = 0; i < n - 1; i++)
{
bool flag = false;
for (int j = 0; j < n - i - 1; j++)//为什么是n-i-1呢,因为第n-i-1个元素是已经排好的
{
if (a[j] > a[j + 1])
{
std::swap(a[j], a[j + 1]);
flag = true;
}
}
if (!flag)
break;
}
}
| 第i趟 | 第i躺排好第几大的值 | 第i趟排好的的第几大的值所在下标 |
|---|---|---|
| 1 | 1 | n-1 |
| 2 | 2 | n-2 |
| 3 | 3 | n-3 |
| … | … | … |
| n-1 | n-1 | 1 |
| n | n | 0 |
相当于就是每次从前往后挪动,都把最大的挪到后面了。以下图为例。


性能分析如下:
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:稳定
3.2 快速排序
快速排序算是排序算法中的重点和难点了,希尔排序是插入排序的优化,那么快速排序就是冒泡排序的优化。事实上,不论是C++STL、Java SDK、.NETFrameWorkSDK等开发工具包中的源代码中都能找到它的某种实现版本。
快速排序是一种分治算法,
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。

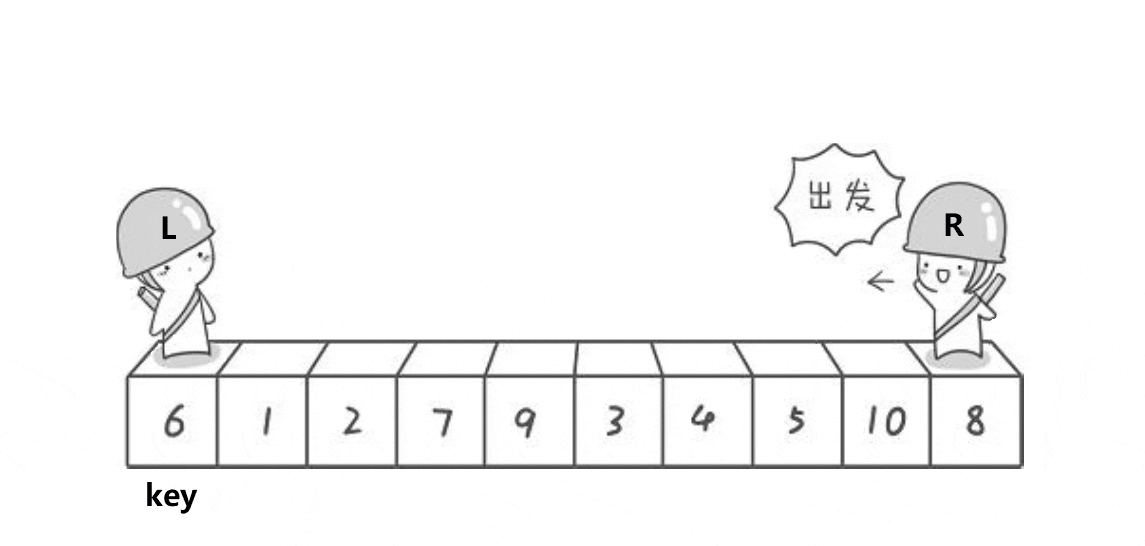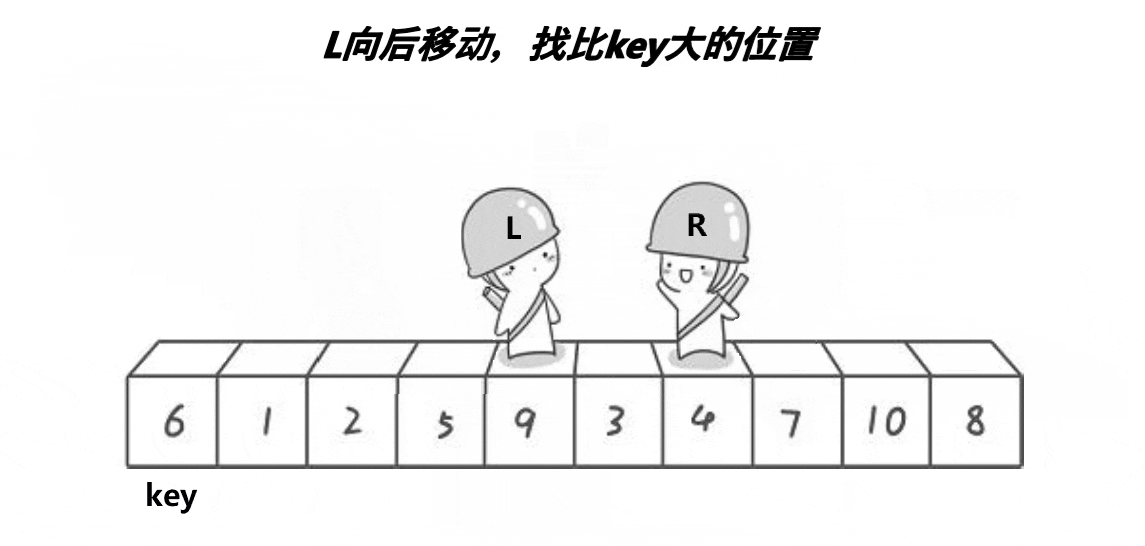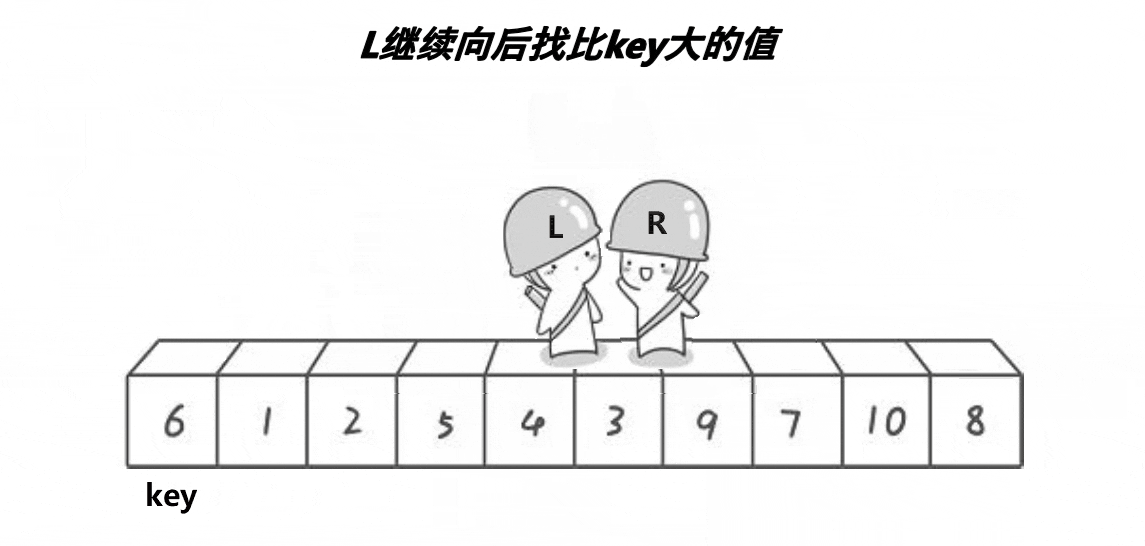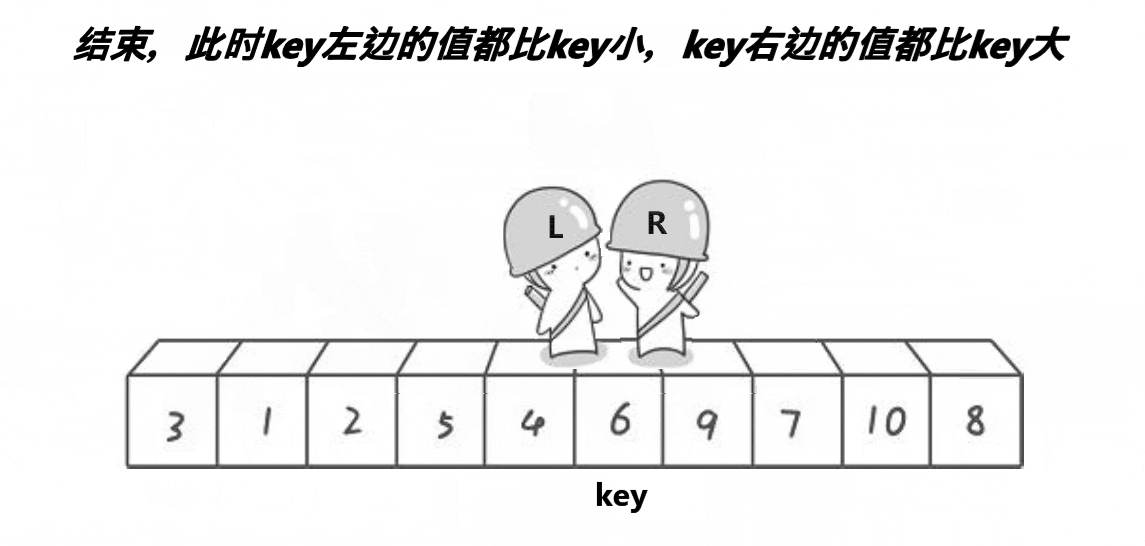
int PartSort(int *a,int left,int right)
{
// 以左边为基准,要先走右找小,再走左找大
int key=left;
while(left<right)
{
while(left<right&&a[right]>=a[key])
{
right--;
}
while(left<right&&a[left]<=a[key])
{
left++;
}
std::swap(a[left],a[right]);
}
std::swap(a[left],a[key]);
return left;
}
// 排序范围[left,right)
void QuickSort(int *a,int left,int right)
{
if(left>=right)
return ;
int key=PartSort(a,left,right);
QuickSort(a,left,key-1);
QuickSort(a,key+1,right);
}
int PartSort(int *a,int left,int right)
{
// 以左边为基准,要先走左找大,再走右找小
int key=right;
while(left<right)
{
while(left<right&&a[left]<=a[key])
{
left++;
}
while(left<right&&a[right]>=a[key])
{
right--;
}
std::swap(a[left],a[right]);
}
std::swap(a[left],a[key]);
return left;
}
// 排序范围[left,right)
void QuickSort(int *a,int left,int right)
{
if(left>=right)
return ;
int key=PartSort(a,left,right);
QuickSort(a,left,key-1);
QuickSort(a,key+1,right);
}
性能分析如下:
空间复杂度:由于利用了递归,需要使用栈,最好情况下为 O ( l o g 2 n ) O(log_2n) O(log2n),最坏情况下为 O ( n ) O(n) O(n),平均情况下为
时间复杂度:快速排序是一种高效的排序算法,其核心思想基于分治法。在最理想的情况下,即每次划分都能将数组分为两个几乎相等的子序列时,快速排序的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。

然而,在最坏的情况下,对逆序和有序的序列使用快速排序,即每次选择的pivot(基准值)都是最大或最小元素,导致每次只能排除一个元素,剩下的元素还需要继续排序,这样会形成类似冒泡排序的情况,需要进行大约n次的划分,每次划分需要遍历几乎所有元素,因此时间复杂度退化为 O ( n 2 ) O(n^2) O(n2)。

稳定性:在划分算法中,若右端区间有两个关键字相同,且均小于基准值的记录,则在交换到左端区间后,它们的相对位置会发生变化,即快速排序是一种不稳定的排序算法。例如,表L={3,2,2},经过一趟排序后L={2,2,3},最终排序序列也是L={2,2.3},显然,2与2的相对次序已发生了变化。
适用性:仅使用与顺序存储的线性表
快速排序可以进行优化,如三数取中。
template <class T>
int minIndex(T *a, int left, int right) // 快速排序三数取中优化法
{
int mid = (left + right) / 2;
if (a[left] < a[right])
{
if (a[mid] < a[left])
{
return left;
}
else if (a[mid] > a[right])
{
return right;
}
else
{
return mid;
}
}
else
{
if (a[mid] > a[left])
{
return left;
}
else if (a[mid] < a[right])
{
return right;
}
else
{
return mid;
}
}
}
4. 选择排序
4.1 简单选择排序
简单选择排序就是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的 数据元素排完 。原理简单,不过多说了。

void SelectSort(int *a, int n)
{
for(int i=0;i<n;i++)
{
int minIndex=i;
for(int j=i;j<n;j++)
{
if(a[minIndex]>a[j])
{
minIndex=j;
}
}
if(minIndex!=i)
std::swap(a[minIndex],a[i]);
}
}
性能分析如下:
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度: O ( n 2 ) O(n^2) O(n2)
稳定性:在第i趟找到最小元素后,和第i个元素交换,可能会导致第i个元素与含有相同关键字的元素的相对位置发生改变。例如,表L={2,2,1},经过一趟排序后L={1,2,2},最终排序序列也是L={1,2.2},显然,2与2的相对次序已发生变化。因此,简单选择排序是一种不稳定的排序算法。
4.2 堆排序
堆排序就是使用堆这种数据结构来进行排序,注意一点,排升序建大堆,排降序建小堆。
每次建完堆后,将堆顶元素与最后一个元素交换,堆顶元素是最大值,然后在此重新向下调整建堆,要注意建堆的范围。


template <class T>
void AdjustDown(T *a, int parent, int n)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])
child++;
if (a[child] < a[parent]) // 小则交换,构建小根堆
{
std::swap(a[child], a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{ // 没有交换则不需要交换
break;
}
}
}
template <class T>
void HeapSort(T *a, int n)
{
for (int i = n - 1 - 1 / 2; i >= 0; i--)
AdjustDown(a, i, n);
for (int i = n - 1; i > 0; i--)
{
std::swap(a[0], a[i]);
AdjustDown(a, 0, i);
}
}
性能分析如下:
空间复杂度: O ( 1 ) O(1) O(1)
时间复杂度:向下调整建堆的时间复杂度为 O ( n ) O(n) O(n),证明过程见树那一章节,每次调整的时间复杂度为 O ( h ) O(h) O(h),故综合时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
稳定性:堆排序可能把有相同关键字元素排到前面,故堆排序不稳定。
5. 归并排序、基数排序、计数排序
5.1 归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
- 把原始需要排序的序列分成两个或多个子序列
- 把每个子序列排好序
- 把多个排好序的子序列合并称一个序列,即为结果


void _Merge(int *a, int left, int right, int *tmp)
{
if (left >= right)
return;
int mid = (left) + (right - left) / 2;
_Merge(a, left, mid, tmp);
_Merge(a, mid + 1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[i++] = a[begin1++];
else
tmp[i++] = a[begin2++];
}
//当遍历完其中一个区间,将另一个区间剩余的数据直接放到tmp的后面
while (begin1 <= end1)
tmp[i++] = a[begin1++];
while (begin2 <= end2)
tmp[i++] = a[begin2++];
// int j=0;
for (int j = left; j <= right; j++)
a[j] = tmp[j];
}
void MergeSort(int *a, int n)
{
int *tmp = (int *)malloc(sizeof(int) * n);
_Merge(a, 0, n - 1, tmp);
free(tmp);
}
5.2 基数排序
对于数字型或字符型的单关键字,可以看成是由多个数位或多个字符构成的多关键字,采用多关键字排序,称作基数排序。
为实现多关键字排序,通常有两种方法:第一种是最高位优先(MSD)法,按关键字位权重递减依次逐层划分成若干更小的子序列,最后将所有子序列依次连接成一个有序序列;第二种是最低位优先(LSD)法,按关键字位权重递增依次进行排序,最后形成一个有序序列。

我们以研究生成绩排序为例,按照分数高低排序,分数相同按专业课排序。
#include <iostream>
#include <vector>
#include <queue>
#include <string>
#include <algorithm>
#include <iomanip>
#include <ctime>
#include "LinkQueue.hpp" //自己在实验2写的链栈
// 基数排序
#define K 3 // 关键字个数 百位、十位、个位
#define Radix 10
struct Student
{
int stuid; // 考生号
std::string name; // 姓名
int totalScore; // 总成绩
int majorScore; // 专业课
Student() {}
// 比较思路如下:
// 进行两次分发回收,第一次以专业课,这样的话总分排序时,专业课高的一定在前面
Student(int id, const std::string n, int t, int m) : stuid(id), name(n), totalScore(t), majorScore(m)
{
}
};
LinkQueue<Student> Q[Radix];
// 基数排序的实现
// 即使用队列将每一次分发的进行存储,每一次分发按照高位到低位进行
int GetKey(int value, int k)
{
int key = 0;
while (k >= 0)
{
key = value % 10;
value /= 10;
k--;
}
return key;
}
void DistributeMajor(std::vector<Student> &a, int left, int right, int k)
{
for (int i = left; i < right; i++)
{
int key = GetKey(a[i].majorScore, k);
Q[key].push(a[i]);
}
}
void DistributeTotal(std::vector<Student> &a, int left, int right, int k)
{
for (int i = left; i < right; i++)
{
int key = GetKey(a[i].totalScore, k);
Q[key].push(a[i]);
}
}
void Collect(std::vector<Student> &a)
{
int k = 0;
for (int i = 0; i < Radix; i++)
{
while (!Q[i].empty())
{
a[k++] = Q[i].front();
Q[i].pop();
}
}
}
void RadixSort(std::vector<Student> &a, int left, int right)
{
for (int i = 0; i < K; i++)
{
DistributeMajor(a, left, right, i);
Collect(a);
}
for (int i = 0; i < K; i++)
{
DistributeTotal(a, left, right, i);
Collect(a);
}
}
int main()
{
std::vector<Student> students = {
{20240001, "Brian", 338, 82},
{20240002, "Queen", 384, 82},
{20240003, "Xiomara", 330, 94},
{20240004, "Gwen", 347, 74},
{20240005, "Ryan", 347, 75},
{20240006, "Holly", 325, 92},
{20240007, "Damon", 399, 88},
{20240008, "Quinn", 440, 120},
{20240009, "Yvette", 306, 94},
{20240010, "Steve", 306, 79},
{20240011, "Mona", 380, 73}};
RadixSort(students, 0, students.size());
std::cout
<< "考生号 "
<< "姓名 "
<< "总分 "
<< "专业课分数" << std::endl;
// 打印学生数据
for (int i = students.size() - 1; i >= 0; i--)
{
std::cout << std::left
<< std::setw(12) << students[i].stuid
<< std::setw(10) << students[i].name
<< std::setw(10) << students[i].totalScore
<< std::setw(12) << students[i].majorScore << std::endl;
}
return 0;
}
| 算法 | 平均时间复杂度 | 最坏时间复杂度 | 额外空间复杂度 | 稳定性 | 说明 |
|---|---|---|---|---|---|
| 简单选择排序 | O(N2) | O(N2) | O(1) | 不稳定 | |
| 冒泡排序 | O(N2) | O(N2) | O(1) | 稳定 | |
| 直接插入排序 | O(N2) | O(N2) | O(1) | 稳定 | |
| 快速排序 | O(NlogN) | O(N2) | O(logN) | 不稳定 | |
| 归并排序 | O(NlogN) | O(NlogN) | O(N) | 稳定 | |
| 堆排序 | O(NlogN) | O(NlogN) | O(1) | 不稳定 | |
| 希尔排序 | O(Nd) | O(N2) | O(1) | 不稳定 | 依赖增量序列d |
| 基数排序 | O(d(N+rd)) | O(d(N+rd)) | O(N+rd) | 稳定 | d是趟数;rd是基数 |
