当前位置：首页 > news >正文

C++————快慢双指针寻找链表循环

news 来源：原创 2025/5/18 21:30:15

在链表中寻找循环点可以使用双指针法，也就是著名的弗洛伊德判圈算法（Floyd's Cycle-Finding Algorithm）。此算法运用两个指针，一个快指针和一个慢指针，借助它们移动速度的差异来判断链表是否存在循环，若存在则找出循环点。

下面是该算法的实现步骤：

初始化指针：让慢指针 slow 和快指针 fast 都指向链表的头节点。
```
ListNode* slow = head;
ListNode* fast = head;
```
判断循环：慢指针每次移动一步，快指针每次移动两步。要是链表存在循环，那么快指针必然会追上慢指针；要是快指针抵达链表末尾（即 fast 或者 fast->next 为 null），就表明链表不存在循环。
```
 // 检测是否存在循环
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        // 快慢指针相遇，说明存在循环
        if (slow == fast) {
        }
    }
```
如果链表有末尾那肯定就不存在循环了。既然有循环，因为快指针每次走2，慢指针每次走了，相当于快指针在慢指针后面追慢指针且每次移动快慢间的距离都减少1，所以必然存在快慢指针相遇的点。

寻找循环点：当快慢指针相遇时，将慢指针重新指向链表的头节点，然后让慢指针和快指针以相同的速度（每次移动一步）继续移动，它们再次相遇的节点就是循环点。

// 检测是否存在循环
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        // 快慢指针相遇，说明存在循环
        if (slow == fast) {
            // 慢指针重新指向头节点
            slow = head;
            while (slow != fast) {
                slow = slow->next;
                fast = fast->next;
            }
            return slow;
        }
    }
    // 没有循环
    return nullptr;

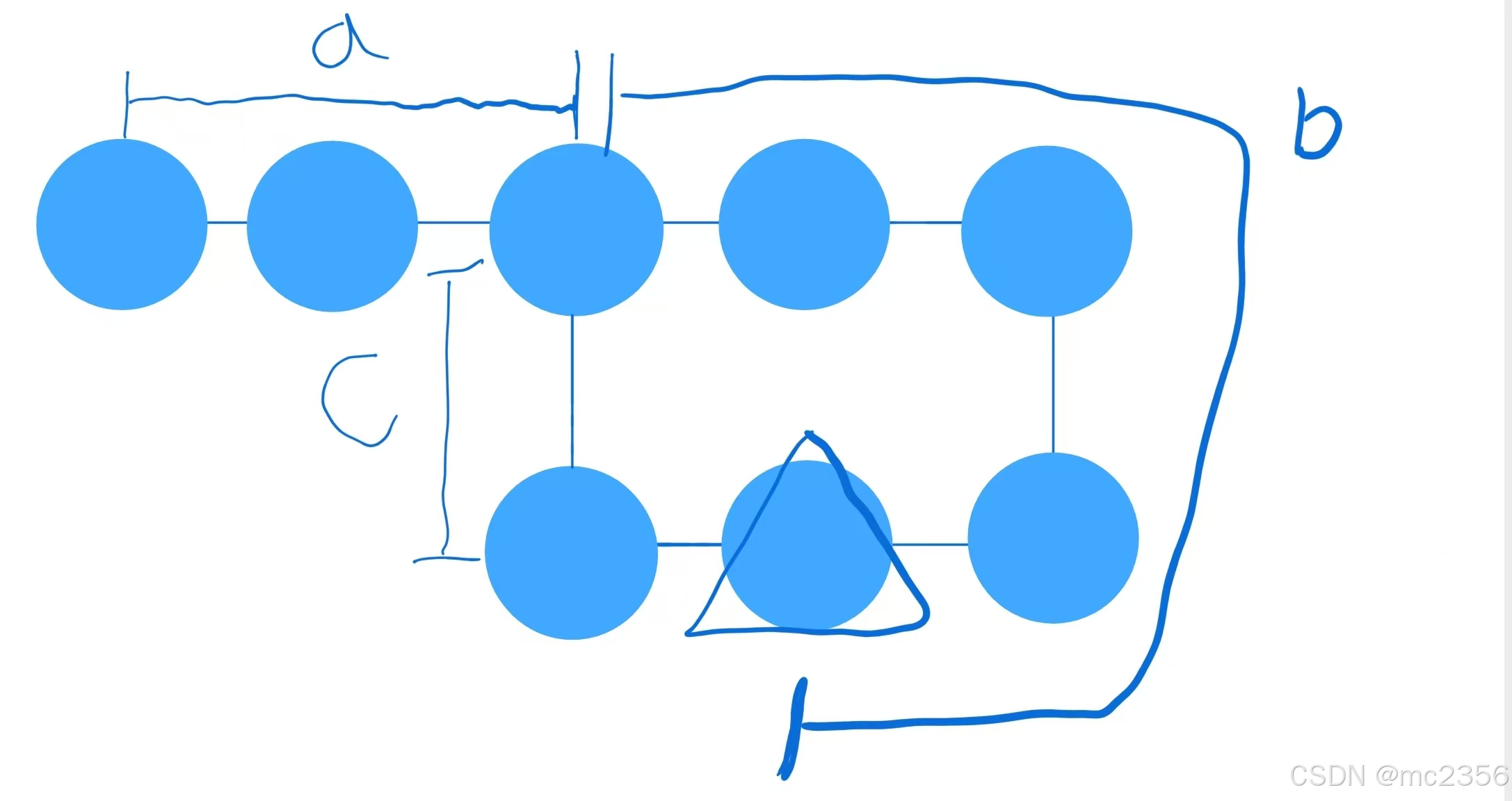
循环的长度L=b+c；

慢指针：设慢指针走过的路程为 $(S_{slow})$ ，因为慢指针每次移动一步，所以 $(S_{slow})$ =a + b。
快指针：设快指针走过的路程为 $(S_{fast})$ ，快指针每次移动两步，由于快指针在慢指针进入循环后又多走了若干圈才和慢指针相遇，设快指针在循环里绕了 n 圈，那么 $(S_{fast}=a + b + nL=a + b+ n(b + c))$ 。
$S fast =2S slow$ ， $(a + b+ n(b + c)=2(a + b))$ ，对该等式进行化简：
(a + b+ n(b + c)=2a + 2b)，
a= n(b + c)-b=(n - 1)(b + c)+c。
如此可见当快指针回到头部并且变为慢指针后，当快指针走到循环点后，慢指针走了a，也就是走了(n - 1)(b + c)+c，即n-1圈和一个c，走到了进入循环的地方，此时两指针相遇返回相遇点。