【算法题解答·六】栈队列堆

【算法题解答·六】栈队列堆

接上文【算法方法总结·六】栈队列堆的一些技巧和注意事项

---

栈队列堆相关题目如下：

232.用栈实现队列 简单

• 准备两个栈，一个负责入队的栈A，一个负责出队的栈B
• 出队和返回队列开头元素，都要先进行以下操作：如果B为空，则A中的元素全部放到B中

class MyQueue {
    Stack<Integer> stackIn;
    Stack<Integer> stackOut;
    public MyQueue() { // 初始化栈
        stackIn = new Stack<>(); // 负责进队
        stackOut = new Stack<>(); // 负责出队
    }
    public void push(int x) { // 入队
        stackIn.push(x);
    }
    public int pop() { // 出队并返回元素
        dumpstackIn();
        return stackOut.pop();
    }
    public int peek() { // 返回队列开头的元素
        dumpstackIn();
        return stackOut.peek();
    }
    public boolean empty() {
        return stackIn.isEmpty() && stackOut.isEmpty();
    }
    // 如果stackOut为空，则stackIn中的元素全部放到stackOut中
    public void dumpstackIn() {
        if (!stackOut.isEmpty())
            return;
        while (!stackIn.isEmpty()) {
            stackOut.push(stackIn.pop());
        }
    }
}

150. 逆波兰表达式求值

• 逆波兰表达式：是一种后缀表达式，所谓后缀就是指运算符写在后面。
• 平常使用的算式则是一种中缀表达式，如 (1+2)*(3+4) 。
• 其逆波兰表达式为 ((1 2+)(3 4+)*)
• 适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> deque = new LinkedList<>();
        for (String s : tokens) {
            if (s.equals("+")) { // 符号，取出两数进行运算，再压入栈中
                deque.push(deque.pop() + deque.pop());
            } else if (s.equals("-")) {
                deque.push(-deque.pop() + deque.pop());
            } else if (s.equals("*")) {
                deque.push(deque.pop() * deque.pop());
            } else if (s.equals("/")) {
                int t1 = deque.pop();
                int t2 = deque.pop();
                deque.push(t2 / t1);
            } else { // 数字入栈
                deque.push(Integer.valueOf(s));
            }
        }
        return deque.pop();
    }
}

239. 滑动窗口最大值 困难

为什么队列用来存下标，是因为需要判断队首元素是否在窗口内

• 使用 由大到小的单调双端队列
• 把比当前元素小的弹出队尾；当前值加入队尾；判断队首元素是否有效；当窗口大于k时，开始记录最大值

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        Deque<Integer> d = new LinkedList<>();
        // 用双端队列存储下标(更方便)
        int n = nums.length;
        int[] res = new int[n - k + 1];
        for (int i = 0; i < n; i++) {
            // 维护单调性，保证从大到小，前面数小依次弹出
            while (!d.isEmpty() && nums[i] >= nums[d.peekLast()]) {
                d.pollLast();
            }
            // 添加当前值对应下标
            d.offerLast(i);
            // 判断队首元素是否有效，[i - k + 1, i]
            if (d.peek() <= i - k) { // 不在范围内
                d.poll();
            }
            // 当窗口长度为k时，保存记录
            if (i + 1 >= k) {
                res[i - k + 1] = nums[d.peek()];
            }
        }
        return res;
    }
}

347.前 K 个高频元素

• 1. 要统计元素出现频率 HashMap
• 2. 对频率排序 PriorityQueue 小根堆
• 3. 找出前K个高频元素

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 小根堆
        PriorityQueue<int[]> p = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
        int[] res = new int[k]; // 保存结果
        Map<Integer, Integer> map = new HashMap<>();
        for (int n : nums) {
            map.put(n, map.getOrDefault(n, 0) + 1);
        }
        for (Map.Entry<Integer, Integer> x : map.entrySet()) {
            int[] tmp = new int[2];
            tmp[0] = x.getKey(); // 元素
            tmp[1] = x.getValue(); // 出现次数
            p.offer(tmp); // (元素,出现次数)
            if (p.size() > k) { // 弹出到只有k个元素，剩下的为最小的k个
                p.poll();
            }
        }
        for (int i = 0; i < k; i++) {
            res[i] = p.poll()[0];
        }
        return res;
    }
}

20.有效的括号 简单

• 遇到左括号( [ {，则让右括号) ] }入栈
• 遇到右括号) ] }，则和 栈顶元素 比较，相同则出栈，最后栈空 说明 有效

class Solution {
    public boolean isValid(String s) {
        Deque<Character> qu = new LinkedList<>(); // 栈
        char[] ss = s.toCharArray();
        for (char ch : ss) {
            if (ch == '(') qu.push(')');
            else if (ch == '[') qu.push(']');
            else if (ch == '{') qu.push('}');
            // 栈空 或 不等于 
            else if (qu.isEmpty() || qu.peek() != ch) {
                return false;
            } else {
                qu.pop();
            }
        }
        return qu.isEmpty();
    }
}

155.最小栈

• 用一个 最小栈 来存储最小元素

class MinStack {
    public Stack<Integer> stack;
    public Stack<Integer> min_stack;
    public MinStack() {
        stack = new Stack<>();
        min_stack = new Stack<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if(min_stack.isEmpty() || val<=min_stack.peek()){
            min_stack.push(val);
        }
    }
    
    public void pop() {
        int x = stack.pop();
        if(x==min_stack.peek()){
            min_stack.pop();
        }
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return min_stack.peek();
    }
}

394.字符串解码

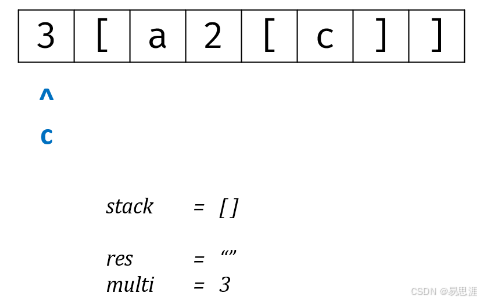
• 情况一：遍历到 [ 时，说明还不需要计算，乘积、字符串res均入栈
• 情况二：遍历到 ] 时，说明需要计算，乘积出栈，当前字符*乘积，拼接上字符串出栈
• 情况三：遍历到0-9时，计算乘积为多少
• 情况四：遍历到字母时，加入res字符串

class Solution {
    public String decodeString(String s) {
        StringBuilder res = new StringBuilder();
        int multi = 0;
        Deque<Integer> st_multi = new LinkedList<>(); //乘积栈
        Deque<String> st_res = new LinkedList<>(); //字符栈
        char[] ss = s.toCharArray();
        for (char ch : ss) {
            if (ch == '[') { //情况一：遍历到 [ 时，加入栈
                st_multi.push(multi); // 乘积入栈
                st_res.push(res.toString()); // 字符入栈
                multi = 0; // 清0
                res = new StringBuilder(); // 清0
            } else if (ch == ']') { //情况二：遍历到 ] 时，出栈
                StringBuilder tmp = new StringBuilder();
                int cur_multi = st_multi.pop(); //乘积
                for (int i = 0; i < cur_multi; i++) {
                    tmp.append(res);
                }
                res = new StringBuilder(st_res.pop() + tmp);
            } else if (ch >= '0' && ch <= '9') { //情况三：遍历到0-9时，计算
                multi = multi * 10 + ch - '0';
            } else { //情况四：遍历到字母时，res
                res.append(ch);
            }
        }
        return res.toString();
    }
}

739.每日温度

• 遍历入栈，下一个要入栈的元素更大，则出栈
• 相当于是一个递减栈，即栈里只有递减元素

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Deque<Integer> qu = new LinkedList<>(); // 栈
        int len = temperatures.length;
        int[] ans = new int[len];
        for (int i = 0; i < len; i++) {
            // 遍历入栈，下一个要入栈的元素更大，则出栈
            // 栈非空，且栈顶温度<当前温度 
            while (!qu.isEmpty() && temperatures[qu.peek()] < temperatures[i]) {
                int idx = qu.pop();
                ans[idx] = i - idx;
            }
            qu.push(i);
        }
        return ans;
    }
}

84.柱状图中最大的矩形 困难

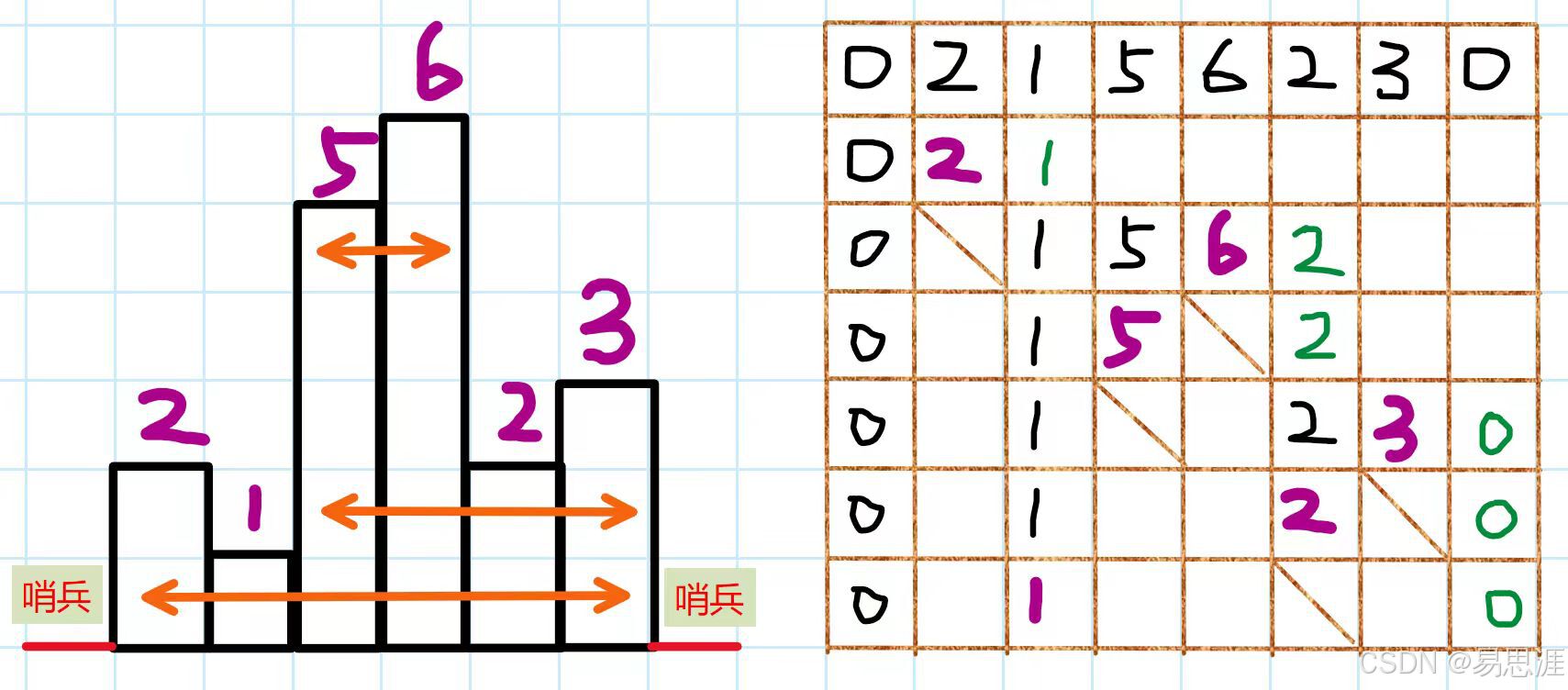
class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        Deque<Integer> st = new LinkedList<>();
        int res = 0;
        // 两端各加一哨兵
        int[] newHeight = new int[len + 2];
        // 数组扩容
        newHeight[0] = 0;
        newHeight[len + 1] = 0;
        for (int i = 0; i < len; i++) {
            newHeight[i + 1] = heights[i];
        }
        heights = newHeight;
        len = heights.length;
        st.push(0);
        for (int i = 1; i < len; i++) {
        	// 有更大的，入栈
            if (heights[i] >= heights[st.peek()]) {
                st.push(i);
            } else {
            	// 下一个准备入栈的元素 < 栈顶，开始计算并出栈
                while (heights[i] < heights[st.peek()]) {
                    int mid = st.pop();
                    int left = st.peek();
                    int right = i;
                    int w = right - left - 1;
                    int h = heights[mid];
                    res = Math.max(res, h * w);
                }
                st.push(i);
            }
        }
        return res;
    }
}

215.数组中的第k个最大元素

• 方法一：内置排序 Arrays.sort() 时间复杂度O(n log n)

• 方法二：快速排序 + 选择

class Solution {
    public int findKthLargest(int[] nums, int k) {
        List<Integer> numList = new ArrayList<>(); // 数组->链表
        for (int num : nums) {
            numList.add(num);
        }
        return quickSelect(numList, k); // 快速排序+选择
    }
    public int quickSelect(List<Integer> nums, int k) {
        // 随机选择哨兵
        Random rand = new Random();
        int pivot = nums.get(rand.nextInt(nums.size()));
        // 划分
        List<Integer> big = new ArrayList<>();
        List<Integer> equal = new ArrayList<>();
        List<Integer> small = new ArrayList<>();
        for (int num : nums) {
            if (num > pivot)
                big.add(num);
            else if (num < pivot)
                small.add(num);
            else
                equal.add(num);
        }
        // 第k大元素在big中，递归划分
        if (k <= big.size()) {
            return quickSelect(big, k);
        }
        // 第k大元素在small中，递归划分
        if (nums.size() - small.size() < k) {
            return quickSelect(small, k - nums.size() + small.size());
        }
        // 第k大元素在equal中，返回pivot
        return pivot;
    }
}

295.数据流的中位数 困难

• A 小根堆 用来保存 较大的一半
• B 大根堆 用来保存 较小的一半

class MedianFinder {
    Queue<Integer> A, B;

    public MedianFinder() {
        A = new PriorityQueue<>(); // 小根堆
        B = new PriorityQueue<>((x, y) -> (y - x)); // 大根堆
    }

    public void addNum(int num) {
        if (A.size() != B.size()) { // 再添加后为偶数
            A.add(num);
            B.add(A.poll());
        } else { // 再添加后为奇数
            B.add(num);
            A.add(B.poll());
        }
    }

    public double findMedian() {
        if (A.size() != B.size()) {
            return A.peek();
        } else {
            return (A.peek() + B.peek()) / 2.0;
        }
    }
}

---

算法题解答系列

【算法题解答·一】二分法
【算法题解答·二】双指针法
【算法题解答·三】滑动窗口
【算法题解答·四】字符串操作
【算法题解答·五】链表操作