9.7 Kochanek-Bartels样条曲线

  在前面的Cutmull-Rom样条曲线中，我们接触到了张力的概念，Kochanek-Bartels样条曲线也是张力可调的算法。Kochanek-Bartels样条曲线也叫TCB样条曲线，是 Tension‑Continuity‑Bias（张力‑连续性‑偏差）的缩写。从名字上可以看出，除了张力可调外，连续性也可以调节，那么连续性究竟怎么调节呢？

连续性可调原理

  前文讲过，连续性$C^1$的曲线，不仅本身连续，其导函数也连续。但是对于TCB样条曲线来说，在每个采样点，切向量分为两个，进入切向量incoming tangent和离开切向量outgoing tangent，TCB通过控制两个切向量的差距，来达到连续性的可控，如果两个切向量相等，那么连续性就是$C^1$,如果两个切向量差别越来越大，连续性就越来越小。如下图：

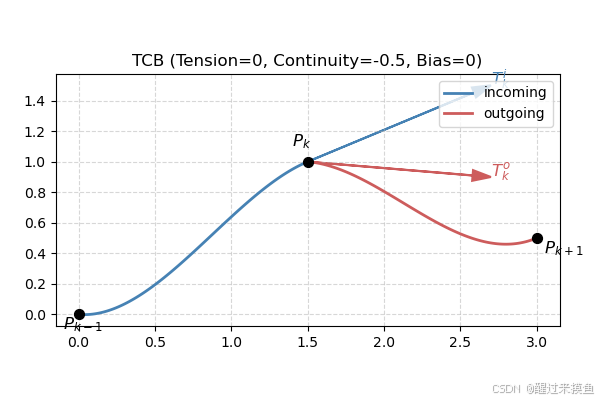
  蓝色的切向量和浅一点曲线相切，红色的切向量和后一段曲线相切。

计算过程

  TCB样条曲线本质上是三阶埃尔米特曲线，埃尔米特曲线由端点的值和导数(切向量)决定。TCB曲线的切向量公式如下：
  进入切向量$T_k^i$
$${\mathbf{T}}_k^i=\frac{(1-{\tau }_k)(1+{\gamma }_k)(1-{\beta }_k)}{2}({\mathbf{P}}_{k+1}-{\mathbf{P}}_k)+\frac{(1-{\tau }_k)(1-{\gamma }_k)(1+{\beta }_k)}{2}({\mathbf{P}}_k-{\mathbf{P}}_{k-1})$$
  离开切向量$T_k^o$:
$${\mathbf{T}}_k^o=\frac{(1-{\tau }_k)(1-{\gamma }_k)(1-{\beta }_k)}{2}({\mathbf{P}}_{k+1}-{\mathbf{P}}_k)+\frac{(1-{\tau }_k)(1+{\gamma }_k)(1+{\beta }_k)}{2}({\mathbf{P}}_k-{\mathbf{P}}_{k-1})$$
  然后分段使用埃尔米特插值就行了。

代码实现

import matplotlib
import numpy as np
import matplotlib.pyplot as pltdef compute_tcb_tangents(P, T=0.0, C=0.0, B=0.0):"""计算每个控制点的切向量（Tangent）.参数:P : (N, d) 控制点数组，N 为点数，d 为维度（2D/3D）。T, C, B : 标量张力、连续性、偏差参数（可为标量或长度为 N 的数组）。返回:T_out : (N, d) 输出切向量（从点 i 指向 i+1 的方向）。T_in  : (N, d) 输入切向量（从点 i 指向 i-1 的方向）。"""N, d = P.shape# 统一为数组形式，便于逐点不同参数T = np.full(N, T) if np.isscalar(T) else np.asarray(T)C = np.full(N, C) if np.isscalar(C) else np.asarray(C)B = np.full(N, B) if np.isscalar(B) else np.asarray(B)# 前后点差分dP_next = np.vstack([P[1:] - P[:-1], np.zeros((1, d))])   # P_{i+1} - P_idP_prev = np.vstack([np.zeros((1, d)), P[1:] - P[:-1]])   # P_i - P_{i-1}# 计算系数a = (1 - T) * (1 + C) * (1 + B) / 2.0b = (1 - T) * (1 - C) * (1 - B) / 2.0c = (1 - T) * (1 - C) * (1 + B) / 2.0d = (1 - T) * (1 + C) * (1 - B) / 2.0# 输出切向量（指向后一个点）T_out = a[:, None] * dP_next + b[:, None] * dP_prev# 输入切向量（指向前一个点）T_in  = c[:, None] * dP_next + d[:, None] * dP_prevreturn T_out, T_indef hermite_segment(P0, P1, T0, T1, n=100):"""生成两点之间的 Hermite 曲线段。参数:P0, P1 : 起止点 (d,)T0, T1 : 起止切向量 (d,)n      : 细分数目返回:(n, d) 曲线点数组"""t = np.linspace(0, 1, n)[:, None]   # (n,1)h00 =  2*t**3 - 3*t**2 + 1h10 =      t**3 - 2*t**2 + th01 = -2*t**3 + 3*t**2h11 =      t**3 -    t**2return h00*P0 + h10*T0 + h01*P1 + h11*T1def tcb_curve(points, tension=0.0, continuity=0.0, bias=0.0, samples_per_seg=50):"""生成完整的 TCB 曲线。参数:points          : (N, d) 控制点tension, continuity, bias : 标量或长度为 N 的数组samples_per_seg  : 每段曲线的采样点数返回:curve_pts : (M, d) 曲线点集合"""P = np.asarray(points, dtype=float)N, d = P.shapeif N < 2:raise ValueError("至少需要两个控制点")# 计算切向量T_out, T_in = compute_tcb_tangents(P, tension, continuity, bias)# 逐段拼接 Hermite 曲线curve = []for i in range(N - 1):seg = hermite_segment(P[i], P[i+1], T_out[i], T_in[i+1], n=samples_per_seg)# 去掉每段的最后一个点（除非是最后一段），避免重复if i < N - 2:seg = seg[:-1]curve.append(seg)return np.vstack(curve)def plot_splines():matplotlib.rcParams['font.family'] = 'Microsoft YaHei'  # Windows 常用# 绘图plt.figure(figsize=(8, 5))# 曲线plt.plot(curve[:, 0], curve[:, 1], 'b-', label='TCB 曲线')# 控制点plt.plot(ctrl_pts[:, 0], ctrl_pts[:, 1], 'ro', label='控制点')# 连线（帮助观察）plt.plot(ctrl_pts[:, 0], ctrl_pts[:, 1], 'k--', linewidth=0.5)plt.title(f'TCB(T={tension},C={continuity},B={bias})曲线示例')plt.legend()plt.axis('equal')plt.grid(True, linestyle='--', alpha=0.6)plt.show()# ------------------- 示例 -------------------
if __name__ == "__main__":# 任意点集（这里演示 2D）ctrl_pts = np.array([[0, 0],[1, 2],[3, 3],[4, 0],[5, -1]])# 可自行修改 T、C、B 参数（这里统一为 0，得到 Catmull‑Rom 曲线）tension = 0.0continuity = 0.0bias = 0.0curve = tcb_curve(ctrl_pts, tension, continuity, bias, samples_per_seg=100)plot_splines()

效果展示

  以下是效果展示: