【具身智能】深入理解3D旋转:从欧拉角、万向锁到四元数与插值算法SLERP
在3D图形学、机器人学和航空航天领域,准确描述和操作“旋转”是一个核心问题。欧拉角因其直观性而被广泛使用,但它带来的“万向锁”问题却臭名昭著。本文将深入探讨万向锁的成因,介绍从根本上解决此问题的四元数,并提供RPY角的直观记忆法和旋转插值技术的原理对比。
一、 欧拉角与万向锁的“纠缠”
什么是欧拉角?
欧拉角(Euler Angles)是一种描述3D空间中物体朝向的最直观方式。它将一个复杂的3D旋转分解为三个按特定顺序进行的、绕着坐标轴(例如X、Y、Z)的简单1D旋转。
例如,一个常见的旋转顺序是 Z-Y-X(偏航-俯仰-滚转)。这意味着:
- 物体首先绕Z轴旋转(Yaw / 偏航)。
- 然后绕新的Y轴旋转(Pitch / 俯仰)。
- 最后绕最新的X轴旋转(Roll / 滚转)。
这种方式非常符合人类的直觉,我们很容易理解“抬头”、“左转”、“侧倾”这些概念。但这种“顺序分解”也正是其“阿喀琉斯之踵”。
万向锁 (Gimbal Lock) —— 自由度的丢失
“万向锁”并不是一个物理的锁,而是欧拉角表示法在特定角度下的一种数学奇异点(Singularity),此时系统会丢失一个旋转自由度。
为了理解它,我们可以想象一个物理的“万向节”(Gimbal),它由三个嵌套的环组成:
- 外环(蓝色):控制偏航 (Yaw),绕Z轴。
- 中环(绿色):控制俯仰 (Pitch),绕Y轴。
- 内环(红色):控制滚转 (Roll),绕X轴。
万向锁的发生过程:
假设我们按照 Z-Y-X 的顺序旋转。
- 我们旋转外环(Yaw)和内环(Roll),一切正常。
- 现在,我们将**中环(Pitch)**旋转了 +90度(或-90度),让物体垂直朝上。
- 灾难发生了: 此时,外环(Yaw)的旋转轴(Z轴)和内环(Roll)的旋转轴(X轴)变得完全重合(都指向了同一个垂直方向)。
- 结果: 无论你现在是转动外环(Yaw)还是内环(Roll),物体的效果都是一样的——它都只是绕着自己的长轴在旋转。
- 丢失的自由度: 你失去了在“水平面”上改变航向的能力。本来的三个独立自由度(Yaw, Pitch, Roll),现在Yaw和Roll变成了同一个东西,系统只剩下两个有效的自由度。
二、 四元数 —— “一步到位”的解决方案
四元数是什么?
四元数(Quaternion)是一种扩展的复数,它有4个分量(w,x,y,zw, x, y, zw,x,y,z),通常写作 q=w+xi+yj+zkq = w + x\mathbf{i} + y\mathbf{j} + z\mathbf{k}q=w+xi+yj+zk。
它在表示旋转时,采用的是完全不同的逻辑:**“轴-角”(Axis-Angle)**表示法。
一个(单位)四元数 qqq 一步到位地描述了一个3D旋转。它定义了:
- 一个3D向量 v⃗=(x,y,z)\vec{v} = (x, y, z)v=(x,y,z) 作为旋转的轴(Axis)。
- 一个角度 θ\thetaθ 作为绕这个轴旋转的角度(Angle)。
(技术上,w=cos(θ/2)w = \cos(\theta/2)w=cos(θ/2),而 (x,y,z)=sin(θ/2)⋅v⃗unit(x, y, z) = \sin(\theta/2) \cdot \vec{v}_{\text{unit}}(x,y,z)=sin(θ/2)⋅vunit)
例如,一个四元数可能会说:“请将物体绕着向量 (0.5, 0.5, 0.707) 旋转 120 度”。
为什么四元数没有万向锁?
答案很简单:四元数不分解旋转,它是一个整体的操作。
- 它根本不关心X、Y、Z轴,也没有“第一步”、“第二步”这样的顺序依赖。
- 它是一个单一、完整的变换。
- 任何3D空间中的朝向都可以用一个四元数来平滑表示,不存在任何“奇异点”或“特殊角度”会导致表示法失效或丢失自由度。
因为它没有“中环转90度”这样的中间步骤,所以它从根本上没有机会让两个轴重合,也就彻底避免了万向锁。
三、 如何直观记忆RPY?
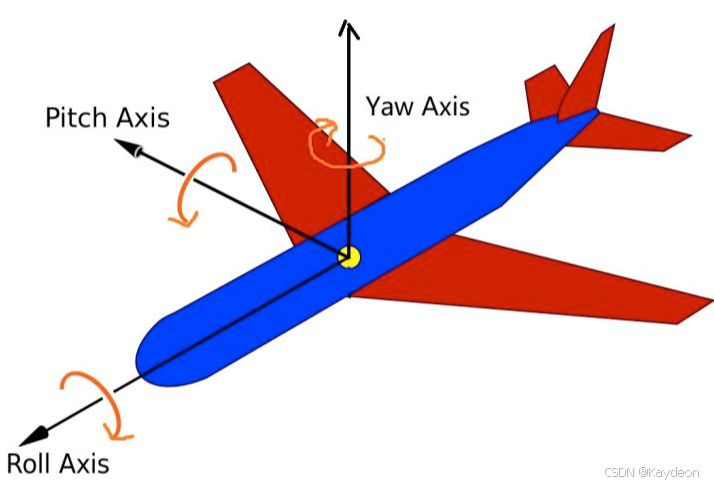
RPY (Roll, Pitch, Yaw) 是欧拉角最常用的一种形式,要记住它们绕哪个轴旋转,最直观的方法是想象一架飞机。
坐标系约定
在航空和机器人领域,一个常见的坐标系约定是:
- X 轴: 指向飞机前方(机头)
- Y 轴: 指向飞机右侧(机翼)
- Z 轴: 指向飞机下方(垂直向下)
RPY 的生动记忆
根据这个模型,三个动作的定义变得非常清晰:
Roll (滚转) →\rightarrow→ 绕 X 轴 (前进轴)
- 动作: 飞机做“桶滚”(Barrel Roll)动作。机身绕着机头到机尾的中心线(X轴)旋转。
- 记忆: Roll 就像木桶在地上滚动。
Pitch (俯仰) →\rightarrow→ 绕 Y 轴 (机翼轴)
- 动作: 飞机“抬头”(爬升)或“低头”(俯冲)。
- 记忆: 投手 (Pitcher) 投球时身体会向前“俯”冲。这个动作的转轴是穿过两侧机翼的Y轴。
Yaw (偏航) →\rightarrow→ 绕 Z 轴 (垂直轴)
- 动作: 飞机在保持水平的同时,机头“向左摆”或“向右摆”。
- 记忆: Yaw 本意即“偏离航向”。这个动作的转轴是垂直穿过飞机中心的Z轴。
四、 旋转插值 —— 平滑过渡的艺术
“插值”是在两个已知的旋转“朝向A”和“朝向B”之间,找到一条平滑的路径。
“坏”的插值:欧拉角的 LERP
最天真的方法是**线性插值(LERP, Linear Interpolation)**欧拉角的三个数字。
例如,从 (10°, 20°, 0°) 插值到 (90°, 60°, 80°)。
为什么这个原理是错的?
- 路径不均匀: 角度的“线性”变化不等于3D空间中“角速度”的均匀变化。物体会时快时慢。
- 路径不“直”: 这不是两个朝向间“最短”的路径。物体会“绕路”,产生奇怪的摇摆。
- 遭遇万向锁: 如果插值路径不幸穿过了万向锁奇点(例如Pitch=90°),插值会彻底崩溃,物体会瞬间“翻转”。
“好”的插值:四元数的 SLERP
四元数使用一种完全不同的插值方法:球面线性插值(SLERP, Spherical Linear Interpolation)。
SLERP 的核心原理(地球比喻):
- 旋转是一个“球面”: 所有可能的3D朝向都存在于一个4D超球体的“表面”上。
- 两个朝向 = 球上的两个城市: “朝向A”和“朝向B”就像是地球仪上的“北京”和“纽约”。
- LERP 的错误: 欧拉角的LERP插值,好比是试图在地图上画直线,然后“挖地道”穿过地球内部来连接两地。
- SLERP 的原理: SLERP 做的,是沿着地球表面找到连接两地的最短路径——即“大圆弧”(Great Circle Arc),也是飞机的最短航线。
SLERP 保证了插值始终在“球面”上(即始终是有效的旋转),并且路径最短、角速度恒定。
SLERP 的数学公式(其中 Ω\OmegaΩ 是两个四元数在4D空间中的夹角):
SLERP(qA,qB,t)=sin((1−t)Ω)sin(Ω)qA+sin(tΩ)sin(Ω)qB \text{SLERP}(q_A, q_B, t) = \frac{\sin((1-t)\Omega)}{\sin(\Omega)}q_A + \frac{\sin(t\Omega)}{\sin(\Omega)}q_B SLERP(qA,qB,t)=sin(Ω)sin((1−t)Ω)qA+sin(Ω)sin(tΩ)qB
五、 总结对比
最后,我们用一个表格来总结欧拉角和四元数的关键区别:
| 特性 (Feature) | 欧拉角 (Euler Angles) | 四元数 (Quaternions) |
|---|---|---|
| 表示方式 | 三个有序的旋转 (如 Z-Y-X) | 一个单一的“轴-角”旋转 |
| 维度 | 3个数字 (α,β,γ\alpha, \beta, \gammaα,β,γ) | 4个数字 (w, x, y, z),受单位长度约束 |
| 核心问题 | 万向锁 (Gimbal Lock):在奇点丢失自由度 | 没有万向锁:表示法在任何角度都健壮 |
| 直观性 | 非常直观:易于人类理解和编辑 | 非常不直观:难以从数字想象旋转 |
| 旋转插值 | LERP:困难且效果差,路径非最短,会抖动 | SLERP:简单且平滑,路径最短,角速度恒定 |
结论
欧拉角因其直观性在用户界面和简单场景中仍有一席之地。但对于任何需要平滑插值(动画、游戏)或复杂姿态控制(机器人、无人机)的严肃应用来说,四元数都是内部表示旋转的黄金标准。
