算法笔记 12 哈希表 | 图

1 同一组数据用字典和哈希表的时空复杂度一样吗？

在大多数语境下（尤其是算法题中），“字典” 和 “哈希表” 本质上是同一种数据结构的不同称呼（哈希表是底层实现，字典是抽象概念），因此对同一组数据的操作，时空复杂度是一样的。

为什么容易混淆？

• “字典” 是一种抽象数据类型（ADT），描述的是 “通过键存储和访问值” 的功能（比如 Python 的dict、C++ 的map/unordered_map都可以称为字典）。
• “哈希表” 是实现 “字典” 功能的一种底层数据结构（通过哈希函数映射键到内存地址，实现快速访问）。

在实际应用中：

• Python 的dict、C++ 的unordered_map、Java 的HashMap，底层都是哈希表实现，因此它们的时空复杂度完全一致。
• 少数情况下，“字典” 可能用其他结构实现（比如 C++ 的map用红黑树实现），但这是特例，此时它的复杂度和哈希表不同（红黑树是 O (log n)，哈希表平均 O (1)）。

哈希表（字典）的时空复杂度

对同一组数据（n 个键值对）：

• 时间复杂度：

  • 插入、查询、删除：平均 O (1)（哈希函数均匀时，直接定位到地址）；
  • 最坏 O (n)（哈希冲突严重，所有键映射到同一位置，退化为链表），但实际中通过优化哈希函数和扩容机制，几乎不会出现。

• 空间复杂度：

  • 存储 n 个元素，需要额外空间存储哈希表结构（如桶数组、链表 / 红黑树节点），总空间复杂度为O(n)。

总结

如果 “字典” 是用哈希表实现的（绝大多数情况），那么对同一组数据的操作，时空复杂度和哈希表完全一致。

只有当 “字典” 用其他结构（如树）实现时，复杂度才会不同。

在算法题中，提到 “字典” 通常默认是哈希表实现，因此可以认为两者复杂度相同。

2 图

第 9 章   图 - Hello 算法

基于邻接矩阵表示图的实现代码（c语言实现）

/* 基于邻接矩阵实现的无向图结构体 */
typedef struct {int vertices[MAX_SIZE];int adjMat[MAX_SIZE][MAX_SIZE];int size;
} GraphAdjMat;/* 构造函数 */
GraphAdjMat *newGraphAdjMat() {GraphAdjMat *graph = (GraphAdjMat *)malloc(sizeof(GraphAdjMat));graph->size = 0;for (int i = 0; i < MAX_SIZE; i++) {for (int j = 0; j < MAX_SIZE; j++) {graph->adjMat[i][j] = 0;}}return graph;
}/* 析构函数 */
void delGraphAdjMat(GraphAdjMat *graph) {free(graph);
}/* 添加顶点 */
void addVertex(GraphAdjMat *graph, int val) {if (graph->size == MAX_SIZE) {fprintf(stderr, "图的顶点数量已达最大值\n");return;}// 添加第 n 个顶点，并将第 n 行和列置零int n = graph->size;graph->vertices[n] = val;for (int i = 0; i <= n; i++) {graph->adjMat[n][i] = graph->adjMat[i][n] = 0;}graph->size++;
}/* 删除顶点 */
void removeVertex(GraphAdjMat *graph, int index) {if (index < 0 || index >= graph->size) {fprintf(stderr, "顶点索引越界\n");return;}// 在顶点列表中移除索引 index 的顶点for (int i = index; i < graph->size - 1; i++) {graph->vertices[i] = graph->vertices[i + 1];}// 在邻接矩阵中删除索引 index 的行for (int i = index; i < graph->size - 1; i++) {for (int j = 0; j < graph->size; j++) {graph->adjMat[i][j] = graph->adjMat[i + 1][j];}}// 在邻接矩阵中删除索引 index 的列for (int i = 0; i < graph->size; i++) {for (int j = index; j < graph->size - 1; j++) {graph->adjMat[i][j] = graph->adjMat[i][j + 1];}}graph->size--;
}/* 添加边 */
// 参数 i, j 对应 vertices 元素索引
void addEdge(GraphAdjMat *graph, int i, int j) {if (i < 0 || j < 0 || i >= graph->size || j >= graph->size || i == j) {fprintf(stderr, "边索引越界或相等\n");return;}graph->adjMat[i][j] = 1;graph->adjMat[j][i] = 1;
}/* 删除边 */
// 参数 i, j 对应 vertices 元素索引
void removeEdge(GraphAdjMat *graph, int i, int j) {if (i < 0 || j < 0 || i >= graph->size || j >= graph->size || i == j) {fprintf(stderr, "边索引越界或相等\n");return;}graph->adjMat[i][j] = 0;graph->adjMat[j][i] = 0;
}/* 打印邻接矩阵 */
void printGraphAdjMat(GraphAdjMat *graph) {printf("顶点列表 = ");printArray(graph->vertices, graph->size);printf("邻接矩阵 =\n");for (int i = 0; i < graph->size; i++) {printArray(graph->adjMat[i], graph->size);}
}

图 | 代码详细解释

一、为什么需要 “图” 这种数据结构？

我们已经学过数组、链表、树，它们能解决很多问题，但有个局限：只能表示 “一对一” 或 “一对多” 的关系。比如：

• 数组 / 链表：每个元素只和前后元素有关（一对一）
• 树：父节点和子节点是一对多

但现实中很多关系是 “多对多” 的：

• 社交网络：每个人可以和多个人是朋友（多对多）
• 地铁线路：每个站点可以连接多个站点（多对多）

这时候就需要图了 —— 它专门用来表示 “多对多” 的关系。

二、图的核心概念（用 “班级同学关系” 举例）

假设我们用图表示班级里的 “朋友关系”：

1. 顶点（Vertex）：每个同学就是一个顶点（比如小明、小红、小刚）
2. 边（Edge）：如果两个同学是朋友，就用一条边连接他们（比如小明 - 小红是朋友，就有一条边）
3. 无向图：边没有方向（小明是小红的朋友，等价于小红是小明的朋友），你提供的代码实现的就是无向图
4. 顶点的 “索引”：为了方便操作，给每个顶点编个号（比如小明 = 0，小红 = 1，小刚 = 2）

三、邻接矩阵：如何用代码存储图？

“邻接矩阵” 是存储图的最直观方式，本质是一个二维数组：

• 行索引 = 顶点 A 的编号
• 列索引 = 顶点 B 的编号
• 数组值 = 1（A 和 B 是朋友）或 0（不是朋友）

比如 3 个同学的关系：

• 小明（0）和小红（1）是朋友
• 小红（1）和小刚（2）是朋友
• 小明（0）和小刚（2）不是朋友

对应的邻接矩阵就是：

行\列 | 0（小明） | 1（小红） | 2（小刚）
---------------------------------------
0    | 0         | 1         | 0       （小明和自己不是朋友，和小红是朋友）
1    | 1         | 0         | 1       （小红和小明是朋友，和自己不是，和小刚是）
2    | 0         | 1         | 0       （小刚和小红是朋友）

注意：无向图的邻接矩阵是对称的（行和列交换后，值不变），因为 “小明 - 小红是朋友” 等价于 “小红 - 小明是朋友”。

四、逐行拆解代码：图的结构体和操作

1. 结构体定义（存储图的 “容器”）

typedef struct {int vertices[MAX_SIZE];    // 存储顶点的值（比如同学的名字用编号代替：0,1,2...）int adjMat[MAX_SIZE][MAX_SIZE];  // 邻接矩阵（存储边的关系）int size;  // 当前图中顶点的实际数量（比如有3个同学，size=3）
} GraphAdjMat;

• MAX_SIZE：提前定义的最大顶点数（比如 #define MAX_SIZE 10，表示最多存 10 个顶点）
• vertices：类似一个数组，vertices[0]就是 0 号顶点的值（比如小明的编号）
• adjMat：二维数组，adjMat[i][j]就是 i 号和 j 号顶点的关系（1 = 有边，0 = 无边）

2. 构造函数（创建一个空图）

GraphAdjMat *newGraphAdjMat() {GraphAdjMat *graph = (GraphAdjMat *)malloc(sizeof(GraphAdjMat));  // 申请内存graph->size = 0;  // 初始时没有顶点，size=0// 初始化邻接矩阵：所有位置先设为0（一开始没有任何边）for (int i = 0; i < MAX_SIZE; i++) {for (int j = 0; j < MAX_SIZE; j++) {graph->adjMat[i][j] = 0;}}return graph;
}

作用：就像买了一个新的笔记本，里面的表格（邻接矩阵）全是空的（0），还没写任何顶点和关系。

3. 添加顶点（往图里加一个 “同学”）

void addVertex(GraphAdjMat *graph, int val) {if (graph->size == MAX_SIZE) {  // 检查是否超过最大容量fprintf(stderr, "图的顶点数量已达最大值\n");return;}int n = graph->size;  // 新顶点的索引是当前size（比如当前有2个顶点，新顶点索引是2）graph->vertices[n] = val;  // 把新顶点的值存在vertices[n]// 初始化新顶点对应的行和列（和已有顶点都先设为0，还没边）for (int i = 0; i <= n; i++) {graph->adjMat[n][i] = 0;  // 新顶点（行n）和所有已有顶点（列i）的边设为0graph->adjMat[i][n] = 0;  // 已有顶点（行i）和新顶点（列n）的边设为0}graph->size++;  // 顶点数量+1
}

举例：

• 初始 size=0，调用addVertex(graph, 10)（添加顶点值 10）：vertices[0] = 10，size 变成 1，邻接矩阵第 0 行第 0 列设为 0（自己和自己没边）。
• 再调用addVertex(graph, 20)：vertices[1] = 20，size 变成 2，邻接矩阵第 1 行第 0 列、第 0 行第 1 列都设为 0（暂时不是朋友）。

4. 添加边（给两个 “同学” 建立朋友关系）

void addEdge(GraphAdjMat *graph, int i, int j) {// 检查索引是否合法（不能越界，不能自己和自己建边）if (i < 0 || j < 0 || i >= graph->size || j >= graph->size || i == j) {fprintf(stderr, "边索引越界或相等\n");return;}graph->adjMat[i][j] = 1;  // i和j有边graph->adjMat[j][i] = 1;  // 无向图，j和i也有边（矩阵对称）
}

举例：

• 现在有两个顶点（索引 0 和 1），调用addEdge(graph, 0, 1)：adjMat[0][1] = 1，adjMat[1][0] = 1（表示 0 和 1 是朋友）。

5. 删除顶点（移除一个 “同学”）

这是最复杂的一步，需要同时删除顶点本身和它所有的边：

void removeVertex(GraphAdjMat *graph, int index) {if (index < 0 || index >= graph->size) {  // 检查索引是否合法fprintf(stderr, "顶点索引越界\n");return;}// 1. 删除顶点列表中的index位置（把后面的顶点往前移）for (int i = index; i < graph->size - 1; i++) {graph->vertices[i] = graph->vertices[i + 1];  // 覆盖当前位置}// 2. 删除邻接矩阵中的index行（把后面的行往上移）for (int i = index; i < graph->size - 1; i++) {for (int j = 0; j < graph->size; j++) {graph->adjMat[i][j] = graph->adjMat[i + 1][j];  // 用下一行覆盖当前行}}// 3. 删除邻接矩阵中的index列（把后面的列往左移）for (int i = 0; i < graph->size; i++) {for (int j = index; j < graph->size - 1; j++) {graph->adjMat[i][j] = graph->adjMat[i][j + 1];  // 用下一列覆盖当前列}}graph->size--;  // 顶点数量-1
}

举例：

• 现在有 3 个顶点（0,1,2），删除索引 1 的顶点：
  1. vertices数组：原本[10,20,30] → 变成[10,30]（20 被移除，后面的 30 前移）。
  2. 邻接矩阵的行：第 1 行被第 2 行覆盖，原本 3 行→变成 2 行。
  3. 邻接矩阵的列：第 1 列被第 2 列覆盖，原本 3 列→变成 2 列。

6. 删除边（解除两个 “同学” 的朋友关系）

void removeEdge(GraphAdjMat *graph, int i, int j) {// 检查索引合法性（和addEdge一样）if (i < 0 || j < 0 || i >= graph->size || j >= graph->size || i == j) {fprintf(stderr, "边索引越界或相等\n");return;}graph->adjMat[i][j] = 0;  // 移除i和j的边graph->adjMat[j][i] = 0;  // 无向图，对称移除
}

五、动手实验：用代码模拟 “同学关系”

写一个main函数，一步步操作，观察输出：

#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 10  // 假设最多10个顶点// （这里粘贴上面的结构体和所有函数）// 辅助函数：打印数组（代码中用到的printArray）
void printArray(int arr[], int size) {printf("[");for (int i = 0; i < size; i++) {printf("%d", arr[i]);if (i < size - 1) printf(", ");}printf("]\n");
}int main() {// 1. 创建空图GraphAdjMat *graph = newGraphAdjMat();printf("初始图（无顶点）：\n");printGraphAdjMat(graph);  // 顶点列表为空，邻接矩阵也为空// 2. 添加3个顶点（小明=10，小红=20，小刚=30）addVertex(graph, 10);addVertex(graph, 20);addVertex(graph, 30);printf("\n添加3个顶点后：\n");printGraphAdjMat(graph);  // 顶点列表[10,20,30]，邻接矩阵全0// 3. 添加边：小明-小红（0-1）、小红-小刚（1-2）addEdge(graph, 0, 1);addEdge(graph, 1, 2);printf("\n添加边后：\n");printGraphAdjMat(graph);  // 邻接矩阵中(0,1),(1,0),(1,2),(2,1)为1// 4. 删除顶点小红（索引1）removeVertex(graph, 1);printf("\n删除小红后：\n");printGraphAdjMat(graph);  // 顶点列表[10,30]，邻接矩阵变为2x2（小红的边全被删除）// 5. 释放内存delGraphAdjMat(graph);return 0;
}

运行后，你会看到每一步操作对 “顶点列表” 和 “邻接矩阵” 的影响，这比单纯看代码更容易理解。

六、总结：关键是理解 “映射关系”

• 顶点列表vertices[i] → 第 i 个顶点的值（是什么）
• 邻接矩阵adjMat[i][j] → 第 i 个和第 j 个顶点的关系（有没有边）
• 所有操作（增删顶点 / 边）都是在维护这两个数组的一致性

3 邻接表的实现方式

要对比邻接矩阵，我们来用 C/C++ 实现邻接表（链表版）和邻接表（哈希表版），并分析它们的特性。

一、邻接表（链表版）实现

邻接表的核心是为每个顶点维护一个链表，存储其直接相连的顶点。

cpp

#include <iostream>
#include <vector>
using namespace std;// 邻接表（链表版）结构体
struct GraphAdjList {vector<vector<int>> adj;  // 每个顶点的邻接链表，adj[i] 存储与 i 直接相连的顶点int size;                 // 顶点数量// 构造函数：初始化 n 个顶点GraphAdjList(int n) {size = n;adj.resize(n);}// 添加边：无向图，i 和 j 互相添加到邻接链表void addEdge(int i, int j) {if (i < 0 || i >= size || j < 0 || j >= size || i == j) {cerr << "边索引越界或相等" << endl;return;}adj[i].push_back(j);adj[j].push_back(i);}// 删除边：在 i 和 j 的邻接链表中移除对方void removeEdge(int i, int j) {if (i < 0 || i >= size || j < 0 || j >= size || i == j) {cerr << "边索引越界或相等" << endl;return;}// 从 i 的邻接链表中删除 jfor (auto it = adj[i].begin(); it != adj[i].end(); ++it) {if (*it == j) {adj[i].erase(it);break;}}// 从 j 的邻接链表中删除 ifor (auto it = adj[j].begin(); it != adj[j].end(); ++it) {if (*it == i) {adj[j].erase(it);break;}}}// 添加顶点：需要重新分配空间（实际工程中一般提前预留，这里简化演示）void addVertex() {adj.push_back(vector<int>());size++;}// 删除顶点：需要删除该顶点的邻接链表，并在所有其他顶点的链表中移除它void removeVertex(int index) {if (index < 0 || index >= size) {cerr << "顶点索引越界" << endl;return;}// 1. 删除该顶点的邻接链表adj.erase(adj.begin() + index);// 2. 在所有其他顶点的邻接链表中移除该顶点for (int i = 0; i < size - 1; ++i) {for (auto it = adj[i].begin(); it != adj[i].end(); ) {if (*it == index) {it = adj[i].erase(it);} else {// 若邻接顶点的索引大于 index，需要减 1（因为顶点 index 被删除了）if (*it > index) {(*it)--;}++it;}}}size--;}// 打印邻接表void print() {for (int i = 0; i < size; ++i) {cout << "顶点 " << i << " 的邻接顶点：";for (int j : adj[i]) {cout << j << " ";}cout << endl;}}
};

二、邻接表（哈希表版）实现

用哈希表（unordered_map）替代链表，能将 “查找邻接顶点” 的时间复杂度优化到 (O(1))。

cpp

#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;// 邻接表（哈希表版）结构体
struct GraphAdjHash {unordered_map<int, unordered_set<int>> adj;  // key：顶点，value：该顶点的邻接顶点集合（哈希表）int size;                                     // 顶点数量// 构造函数：初始化 n 个顶点GraphAdjHash(int n) {size = n;for (int i = 0; i < n; ++i) {adj[i] = unordered_set<int>();}}// 添加边：无向图，i 和 j 互相添加到邻接集合void addEdge(int i, int j) {if (i < 0 || i >= size || j < 0 || j >= size || i == j) {cerr << "边索引越界或相等" << endl;return;}adj[i].insert(j);adj[j].insert(i);}// 删除边：在 i 和 j 的邻接集合中移除对方void removeEdge(int i, int j) {if (i < 0 || i >= size || j < 0 || j >= size || i == j) {cerr << "边索引越界或相等" << endl;return;}adj[i].erase(j);adj[j].erase(i);}// 添加顶点void addVertex() {adj[size] = unordered_set<int>();size++;}// 删除顶点：删除该顶点的邻接集合，并在所有其他顶点的集合中移除它void removeVertex(int index) {if (index < 0 || index >= size) {cerr << "顶点索引越界" << endl;return;}// 1. 删除该顶点的邻接集合adj.erase(index);// 2. 在所有其他顶点的邻接集合中移除该顶点for (auto& [v, neighbors] : adj) {neighbors.erase(index);}size--;}// 打印邻接表void print() {for (auto& [v, neighbors] : adj) {cout << "顶点 " << v << " 的邻接顶点：";for (int n : neighbors) {cout << n << " ";}cout << endl;}}
};

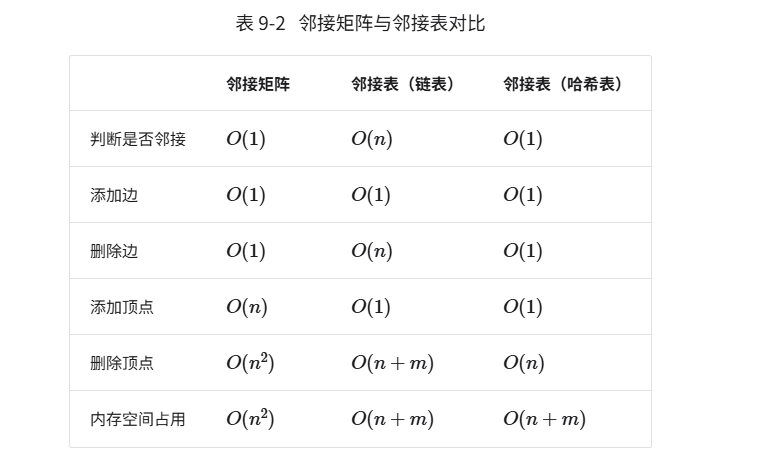
三、三种实现的核心对比（结合你提供的表格）

操作	邻接矩阵 （时间复杂度）	邻接表 （链表版）	邻接表 （哈希表版）	说明
判断是否邻接	(O(1))	(O(n))	(O(1))	邻接矩阵直接查adjMat[i][j]；链表需遍历链表；哈希表直接查集合
添加边	(O(1))	(O(1))	(O(1))	矩阵改一个值；链表 / 哈希表添加到邻接结构
删除边	(O(1))	(O(n))	(O(1))	矩阵改一个值；链表需遍历找节点；哈希表直接删除集合元素
添加顶点	(O(n^2))	(O(1))	(O(1))	邻接矩阵需初始化新的行和列；链表 / 哈希表只需新增一个空结构
删除顶点	(O(n^2))	(O(n+m))	(O(n))	邻接矩阵需移动所有行和列；链表需处理所有邻接链表；哈希表删除键后遍历所有集合
内存空间占用	(O(n^2))	(O(n+m))	(O(n+m))	n 是顶点数，m 是边数；矩阵是固定二维数组，邻接表只存实际边

四、如何选择？

• 邻接矩阵：适合顶点数少、边数多的 “稠密图”（比如完全图），优点是实现简单、判断邻接极快。
• 邻接表（链表版）：适合顶点数多、边数少的 “稀疏图”，内存更高效，但查找邻接顶点较慢。
• 邻接表（哈希表版）：在链表版的基础上优化了 “查找 / 删除邻接顶点” 的效率，是工程中更实用的选择。

4 图的重点回顾

1. “图由顶点和边组成，可以表示为一组顶点和一组边构成的集合。”

• 顶点：就是 “点”，比如社交网络里的 “人”、地铁图里的 “站点”。
• 边：就是连接顶点的 “线”，表示顶点之间的关系，比如 “朋友关系”“地铁线路”。
• 例子：把你、我、他看成三个顶点，“是朋友” 看成边，那么 “图” 就是 {你，我，他}（顶点集合） + {你 - 我，我 - 他}（边集合）。

2. “相较于线性关系（链表）和分治关系（树），网络关系（图）具有更高的自由度，因而更为复杂。”

• 线性结构（链表）：元素是 “一对一” 的，比如链表的每个节点只有一个前驱、一个后继。
• 分治结构（树）：元素是 “一对多” 的，比如树的父节点可以有多个子节点，但子节点只有一个父节点。
• 图（网络结构）：元素是 “多对多” 的，一个顶点可以和任意多个顶点相连，所以关系更自由、更复杂。

3. “有向图的边具有方向性，连通图中的任意顶点均可达，有权图的每条边都包含权重变量。”

• 有向图：边是有方向的，比如 “微博关注”（我关注你，你不一定关注我），边要画箭头。
• 连通图：图里任意两个顶点，都能通过边 “走通”，比如一个没有孤岛的地铁网。
• 有权图：边带有 “权重”（可以理解为 “成本” 或 “距离”），比如地图里的 “两点间距离”“打车费用”。

4. “邻接矩阵利用矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，用 1 或 0 表示两个顶点之间有边或无边。邻接矩阵在增删查改操作上效率很高，但空间占用较多。”

• 邻接矩阵是一个二维数组：行和列都是顶点，matrix[i][j] = 1 表示顶点i和j有边，0表示无边。
• 效率高：判断 “两个顶点是否相连” 只要看数组里的一个值（时间复杂度 (O(1))）；添加 / 删除边也只要改一个值。
• 空间占用多：如果有n个顶点，矩阵是n×n的，哪怕边很少（比如稀疏图），也得占n²的空间。

5. “邻接表使用多个链表来表示图，第 i 个链表对应顶点 i，其中存储了该顶点的所有邻接顶点。邻接表相对于邻接矩阵更加节省空间，但由于需要遍历链表来查找边，因此时间效率较低。”

• 邻接表是 “顶点→链表” 的结构：每个顶点对应一个链表，链表存的是和它直接相连的顶点。
• 节省空间：如果有n个顶点、m条边，邻接表只需要存 n + m 的空间（每个顶点一个链表，每条边存两次，因为无向图）。
• 时间效率低：判断 “顶点 i 和 j 是否相连”，需要遍历顶点i的链表找j，最坏情况要遍历整个链表（时间复杂度 (O(n)) ）。

6. “当邻接表中的链表过长时，可将其转换为红黑树或哈希表，从而提升查询效率。”

• 链表的缺点是 “查找慢”，所以可以把 “链表” 换成红黑树（有序，查找时间\(O(log n)\)）或哈希表（查找时间\(O(1)\)），这样查邻接顶点就快了，这就是你之前问的 “哈希表版邻接表”~

7. “从算法思想的角度分析，邻接矩阵体现了‘以空间换时间’，邻接表体现了‘以时间换空间’。”

• 邻接矩阵：用 “大空间”（(n²)的矩阵）换 “快时间”（增删查改(O(1))）。
• 邻接表：用 “小空间”（(n+m)）换 “慢时间”（查找(O(n))或(O(log n))）。

8. “图可用于建模各类现实系统，如社交网络、地铁线路等。”

• 社交网络：顶点 = 用户，边 = 好友关系。
• 地铁线路：顶点 = 站点，边 = 地铁线，权重 = 站数 / 时间。
• 还有：电路（顶点 = 元件，边 = 导线）、网页链接（顶点 = 网页，边 = 超链接）……

9. “树是图的一种特例，树的遍历也是图的遍历的一种特例。”

• 树：是 “没有环的连通无向图”（比如家族树，每个节点只有一个父节点，没有循环）。
• 所以树的 “前序、中序、后序遍历” 其实是图的 “深度优先遍历（DFS）” 的特例；树的 “层序遍历” 是图的 “广度优先遍历（BFS）” 的特例。

10. “图的广度优先遍历是一种由近及远、层层扩张的搜索方式，通常借助队列实现。”

• 想象 “水波扩散”：先访问起点，再访问起点的所有邻居，再访问邻居的邻居……
• 实现：用队列，把顶点 “入队→访问→把邻居入队”，循环直到队空。

11. “图的深度优先遍历是一种优先走到底、无路可走时再回溯的搜索方式，常基于递归来实现。”

• 想象 “走迷宫”：沿着一条路走到头，没路了就回到上一个岔口走另一条……
• 实现：递归（或栈），访问顶点→递归访问它的邻居（没访问过的）。