当前位置：首页 > news >正文

数据结构入门 (十一)：“自我平衡”的艺术 —— 详解AVL树

news 2025/11/16 7:06:14

文章目录

引言：当“秩序”走向“极端”
一、平衡的“标尺”：平衡因子 (BF)
二、“拨乱反正”：AVL树的四种旋转
- - 1. LL 型（左左）：右旋
  - 2. RR 型（右右）：左旋
  - 3. LR 型（左右）：先左旋再右旋
  - 4. RL 型（右左）：先右旋再左旋
三、AVL树的C语言实现
- 1. 结构设计
- 2. 核心辅助函数
- 3. 旋转操作 (核心)
- 4. 插入操作 (带平衡调整)
- 5. 删除操作 (带平衡调整)
四、总结：严格平衡的“代价”

引言：当“秩序”走向“极端”

在上一篇文章中，我们见证了二叉搜索树（BST）的强大——它依靠“左小右大”的秩序，在平均情况下提供了 O(log n) 的高效操作。

然而，这份“秩序”是脆弱的。如果我们按顺序 (1, 2, 3, 4, 5) 插入数据，会发现了一个大大的问题：，BST会退化成一条单链表，所有操作的效率也随之退化到 O(n)。我们精心构建的“秩序”反而成了我们的枷锁。

![BST退化成链表的示意图]

BST退化成链表

为了让操作效率始终保持在O(logn)，两位苏联数学家 Adelson-Velsky 和 Landis 在1962年提出了一种严格的自平衡结构——AVL树。

一、平衡的“标尺”：平衡因子 (BF)

AVL 树的实现，就是在二叉搜索树的基础上，增加了一条“铁律”：
树中任意一个节点的左、右子树的高度差（平衡因子），其绝对值不能超过1。

平衡因子 (BF) = 左子树高度 - 右子树高度

因此，在一个合法的 AVL 树中，每个节点的平衡因子 BF 只能是：

1：左子树比右子树高1层（左高）。
0：左、右子树等高。
-1：右子树比左子树高1层（右高）。

一旦某个节点的 BF 变成了 2 或 -2，就说明树“失衡”了，必须立刻进行调整。

二、“拨乱反正”：AVL树的四种旋转

AVL 树保持平衡的秘诀，就在于它在插入或删除后，会沿着路径回溯，检查路径上所有祖先节点的平衡因子。一旦发现失衡（BF 变为 ±2），就会立即启动“旋转”操作，进行局部重构，使子树恢复平衡。

旋转的本质是在保持BST“左小右大”性质（即中序遍历不变）的前提下，通过指针的挪移来降低子树的高度。

根据新节点插入的位置，有四种失衡情况：

1. LL 型（左左）：右旋

成因：新节点插入到了“失衡节点”31的左子树的左侧。
表现：31 的 BF 变为 2，31 的左孩子 26 的 BF 变为 1。

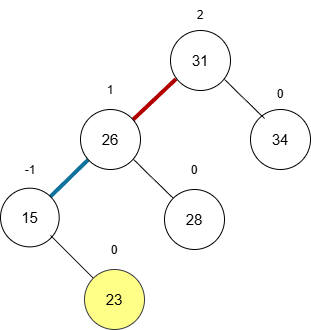
请添加图片描述

调整：对 26 进行右旋。
- 26 提拔为新的根。
- 31 降级为 26 的右孩子。
- 26 原来的右子树（28）“过继”给 31，成为 31 的左子树。

2. RR 型（右右）：左旋

成因：新节点插入到了“失衡节点”56 的右子树的右侧。
表现：56 的 BF 变为 -2，56 的右孩子 78 的 BF 变为 -1。
调整：对 56 进行左旋。
- 78 提拔为新的根。
- 56 降级为 78 的左孩子。
- 78 原来的左子树（66）“过继”给 56，成为 56 的右子树。

3. LR 型（左右）：先左旋再右旋

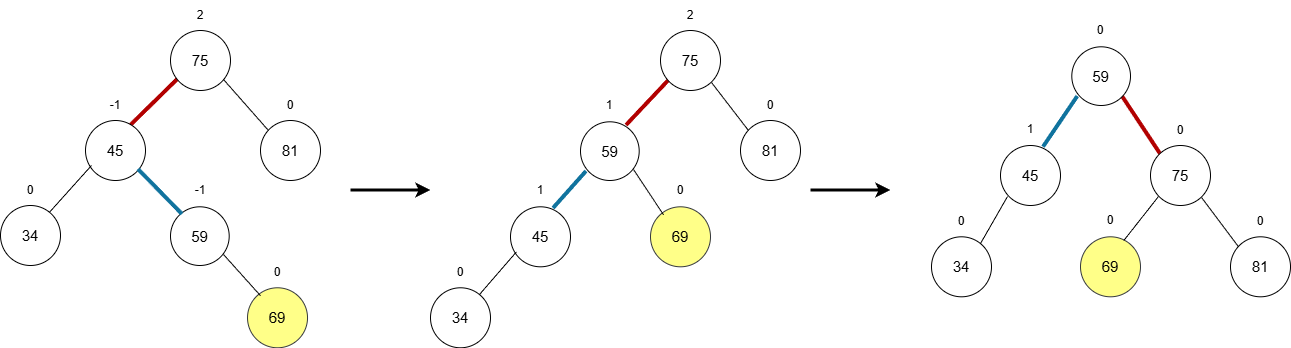
成因：新节点插入到了“失衡节点”75 的左子树的右侧。
表现：75 的 BF 变为 2，75的左孩子 45 的 BF 变为 -1。
调整：
1. 对 45 (75的左孩子) 进行一次左旋，将其转化为 LL 型。
2. 对 75 (失衡节点) 进行一次右旋。

请添加图片描述

4. RL 型（右左）：先右旋再左旋

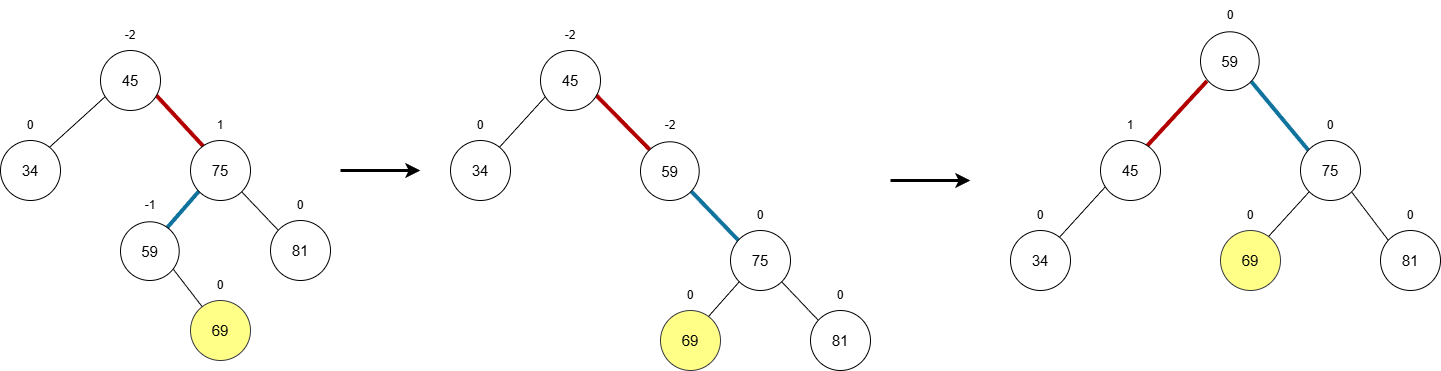
成因：新节点插入到了“失衡节点”45 的右子树的左侧。
表现：45 的 BF 变为 -2，A 的右孩子 75 的 BF 变为 1。
调整：
1. 对 75 (45的右孩子) 进行一次右旋，将其转化为 RR 型。
2. 对 45 (失衡节点) 进行一次左旋。

三、AVL树的C语言实现

1. 结构设计

每个节点必须额外存储 height（高度）字段，平衡因子 BF 可以通过左右子树的 height 动态计算得出。

#include <stdio.h>
#include <stdlib.h>typedef int Element;
// 平衡二叉树的节点结构
typedef struct _avl_Node
{Element data;struct _avl_Node *left, *right;int height; // 节点高度 (以该节点为根的子树的最大高度)
} AVLNode;// 平衡二叉树的树头结构
typedef struct
{AVLNode *root;int count;
} AVLTree;

2. 核心辅助函数

// 获取节点高度（NULL节点高度为0）
static int h(AVLNode *node) {if (node == NULL) {return 0;}return node->height;
}// 比较并取更大值
static int maxNum(int a, int b) {return (a > b) ? a : b;
}// 计算平衡因子
static int getBalance(const AVLNode *node) {if (node == NULL) {return 0;}return h(node->left) - h(node->right);
}// 创建一个新节点
static AVLNode *createAVLNode(Element data, AVLTree* tree) {AVLNode *node = (AVLNode*)malloc(sizeof(AVLNode));if (node == NULL) {return NULL;}node->data = data;node->left = node->right = NULL;node->height = 1; // 新节点高度默认为1tree->count++;return node;
}

3. 旋转操作 (核心)

/* 左旋操作*      px              px*      |               |*      x               y*    /  \    --->    /  \*   lx   y          x    ry*       / \        / \*     ly  ry     lx  ly*/
static AVLNode *leftRotate(AVLNode *x)
{AVLNode* y = x->right;x->right = y->left;y->left = x;// 更新高度（必须先更新x，再更新y）x->height = maxNum(h(x->left), h(x->right)) + 1;y->height = maxNum(h(y->left), h(y->right)) + 1;return y;
}/*      py              py*      |               |*      y               x*    /  \    --->    /  \*   x    ry         lx   y*  / \                  / \* lx  rx               rx  ry*/
static AVLNode *rightRotate(AVLNode *y)
{AVLNode* x = y->left;y->left = x->right;x->right = y;// 更新高度（必须先更新y，再更新x）y->height = maxNum(h(x->left), h(x->right)) + 1;x->height = maxNum(h(y->left), h(y->right)) + 1;return y;
}

4. 插入操作 (带平衡调整)

AVL 树的插入，就是在 BST 插入的递归回溯过程中，增加了检查平衡并执行旋转的步骤。

// 插入的递归辅助函数
static AVLNode *insertAVLNode(AVLTree* tree, AVLNode *node, Element e) {// 1. 递归的初始化位置if (node == NULL) {return createAVLNode(e, tree);}// 递的过程if (e < node->data) {node->left = insertAVLNode(tree, node->left, e);} else if (e > node->data) {node->right = insertAVLNode(tree, node->right, e);} else {return node; // 不允许插入重复值}// 2. 此时的代码，已经进入到归的过程，更新这条路径上节点高度，同时检测平衡因子// 2.1 归过程中的节点高度的更新updateHeight(node);// 2.2 计算当前节点的平衡因子int balance = getBalance(node);// 3. 检查是否失衡，并执行相应旋转if (balance > 1) {// 左边的高度大了if (e > node->left->data) {// LRnode->left = leftRotate(node->left);}// LLreturn rightRotate(node);}if (balance < -1){if (e < node->right->data) {// RLnode->right = rightRotate(node->right);}// RRreturn leftRotate(node);}return node;
}// 对外接口：插入
void insertAVLTree(AVLTree* tree, Element data) {if (tree) {tree->root = insertAVLNode(tree, tree->root, data);}
}

5. 删除操作 (带平衡调整)

删除操作与插入类似，但在删除节点后（尤其是度为2的节点，替换前驱/后继后），也需要在回溯路径上检查平衡性并进行旋转。

// 删除的递归辅助函数
static AVLNode *deleteAVLNode(AVLTree *tree, AVLNode *node, Element e) {if (node == NULL) {return NULL; // 未找到}// 1. 找到要删除的节点if (e < node->data) {node->left = deleteAVLNode(tree, node->left, e);} else if (e > node->data) {node->right = deleteAVLNode(tree, node->right, e);} else {// 找到了,执行删除AVLNode *tmp;if (node->left == NULL || node->right == NULL) {tmp = node->left ? node->left : node->right;if (tmp == NULL) {// 度为0，直接删除tree->count--;free(node);return NULL;}// 度为1，将tmp的值总结替换成nodenode->data = tmp->data;node->left = tmp->left;node->right = tmp->right;tree->count--;free(tmp);} else {// 度为2的点，找前驱节点tmp = node->left;while (tmp->right) {tmp = tmp->right;}node->data = tmp->data;node->left = deleteAVLNode(tree, node->left, tmp->data);}}// 2.归的过程中，更新平衡因子updateHeight(node);// 3. 计算平衡因子int balance = getBalance(node);// 4. 检查并执行旋转 (逻辑与插入时类似，但判断条件略有不同)if (balance > 1) {if (getBalance(node->left) < 0) {node->left = leftRotate(node->left);}return rightRotate(node);}if (balance < -1) {if (getBalance(node->right) > 0) {node->right = rightRotate(node->right);}return leftRotate(node);}return node;
}// 对外接口：删除
void deleteAVLTree(AVLTree* tree, Element e) {if (tree) {tree->root = deleteAVLNode(tree, tree->root, e);}
}