计算机图形学·15 计算机视图(Computer Viewing)
本文是记录专业课计算机图形学的部分笔记,参考教材为Angel的第八版交互式计算机图形学——基于WebGL 2.0的自顶向下方法。
1、在计算机视图(Computer Viewing)中视图有三个功能,都在流水线体系中实现,分别是定位照相机(设置model-view matrix)、设置镜头(设置投影矩阵)、裁剪(设置视见体)。流水线如下所示:
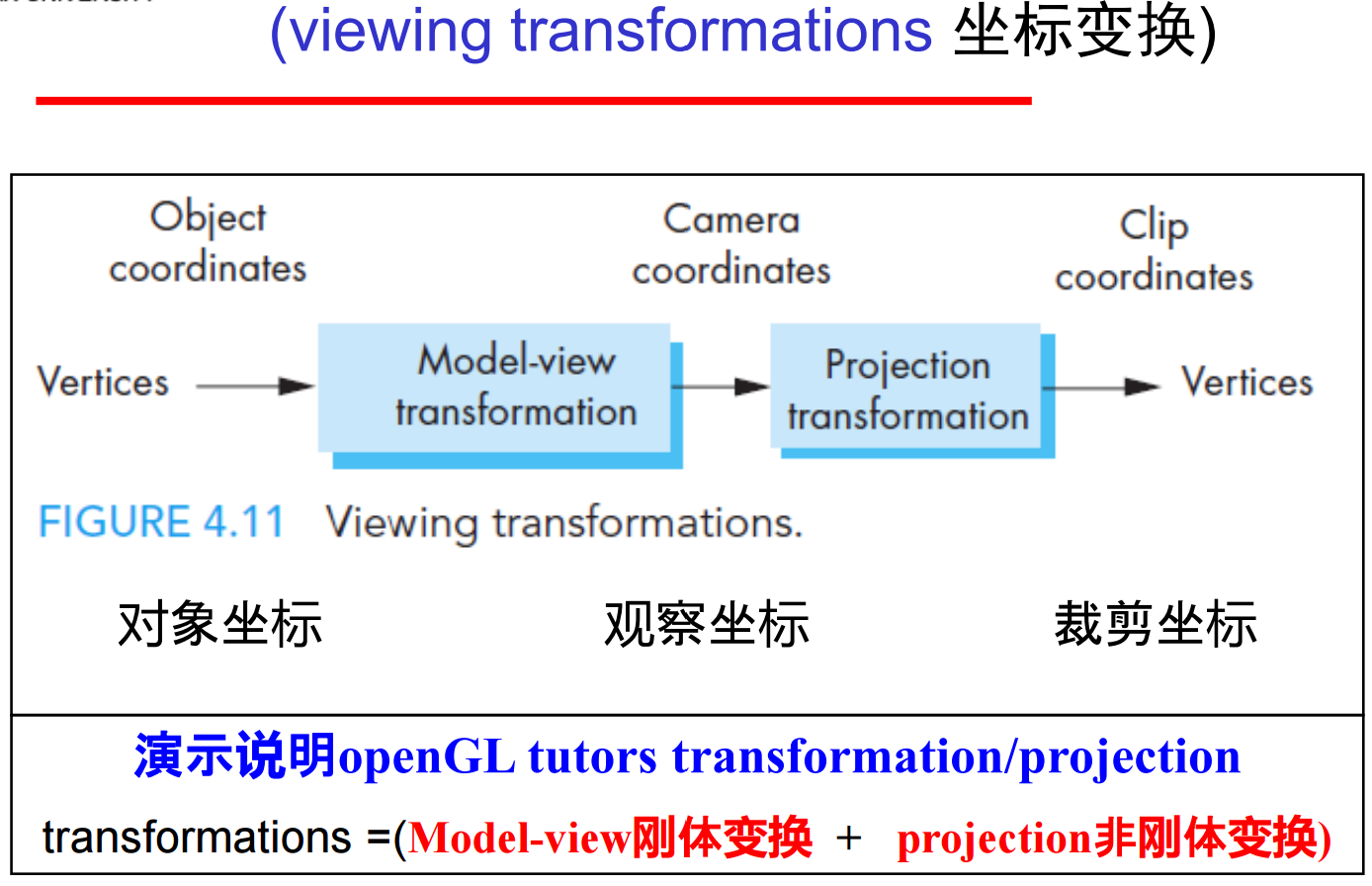
2、计算机视图是基于合成照相机的,原则上可以实现所有的经典视图。所有的经典视图是基于对象、观察者和投影线之间的紧密联系的,而在计算机图形学中强调的则是对象定义与照相机定义之间的独立性。在OpenGL中可以指定采用的是透视投影或者正交投影,但在透视投影中OpenGL并不知道什么是单点、两点或三点透视(为了实现这些细节,需要知道对象与照相机之间的关系,设定参数)。
3、计算机视图最终的选择是偏好对象定义与照相机定义之间的独立性。如果应用程序需要特定类型的视图,那么应当仔细确定照相机相对于对象的位置,因为在透视投影中,从射影几何的角度来说,一般情况下,有三个灭点(一个灭点、二个灭点是特例)。在OpenGL中,初始的世界标架和照相机标架相同,即初始的模型-视图矩阵是单位阵,照相机位于原点,并指向z轴的负向(-z方向,视点方向)。OpenGL也指定了默认的视景体,它是一个中心在原点的边长为2的立方体;缺省的投影矩阵是单位阵,最简单正投影:
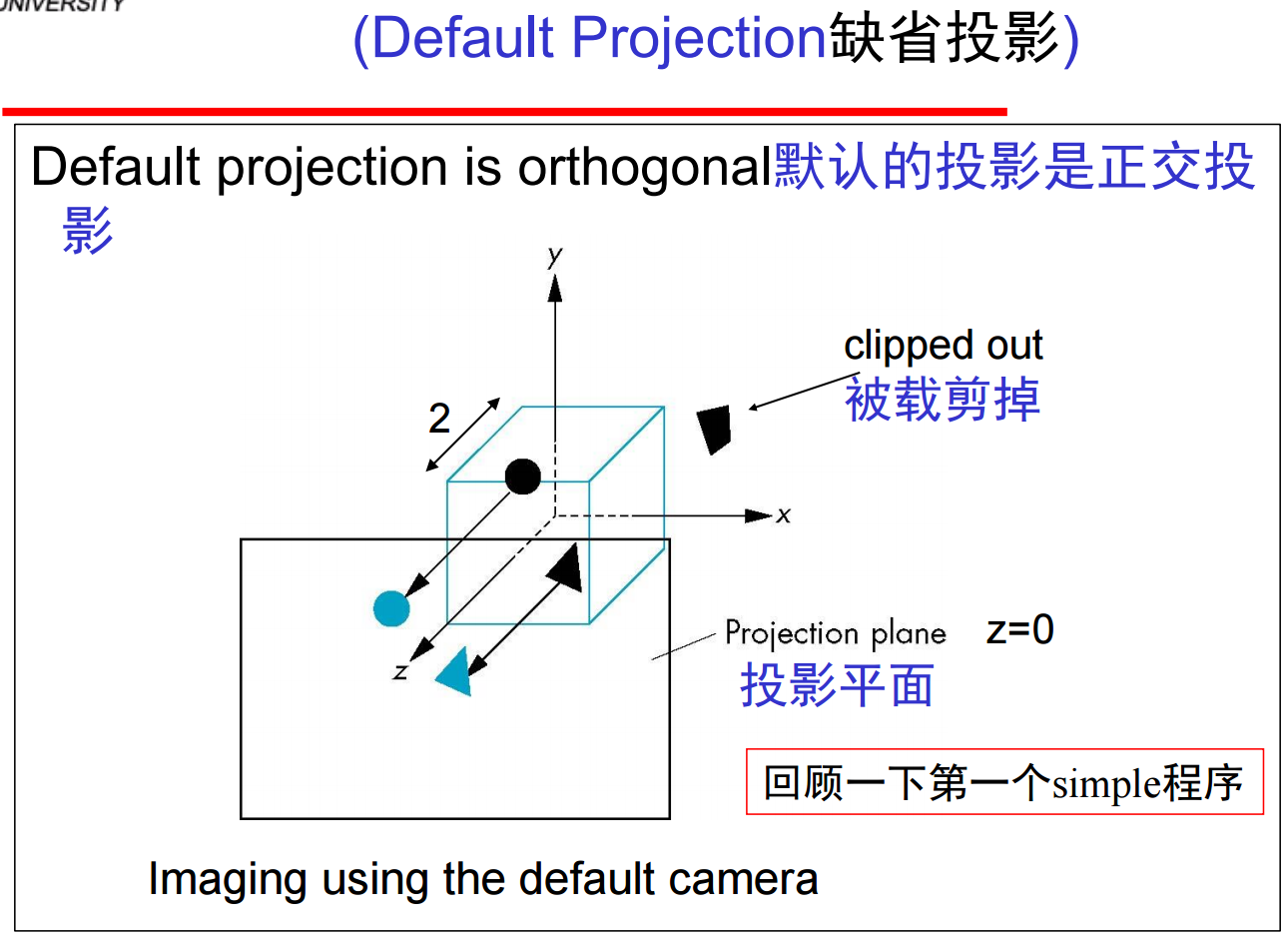
4、在缺省的照相机设置下,为了使定义的对象可见,只要使对象的位置和尺寸与默认视景体相匹配,原理上可以对数据对象进行适当的平移和各向同性放缩来实现,注意这并不是利用OpenGL的平移和放缩函数进行的操作,而是观察变换Transformation方法(第一类观察API,例如 gllookat函数;第二类观察API,例如Orthogonal 正交投影函数)。
如何理解?(对象不变!而是改变标架)
最终通过(Model-view刚体变换 + projection非刚体变换)
5、如果想看到更大的正z坐标的对象,可以把照相机沿z轴正向移动(移动照相机标架),或把对象沿z轴负向移动(移动世界标架),这两者是完全等价的,都是由模型-视图矩阵确定的(需要平移glTranslated(0.0, 0.0, -d); 此处d > 0)。
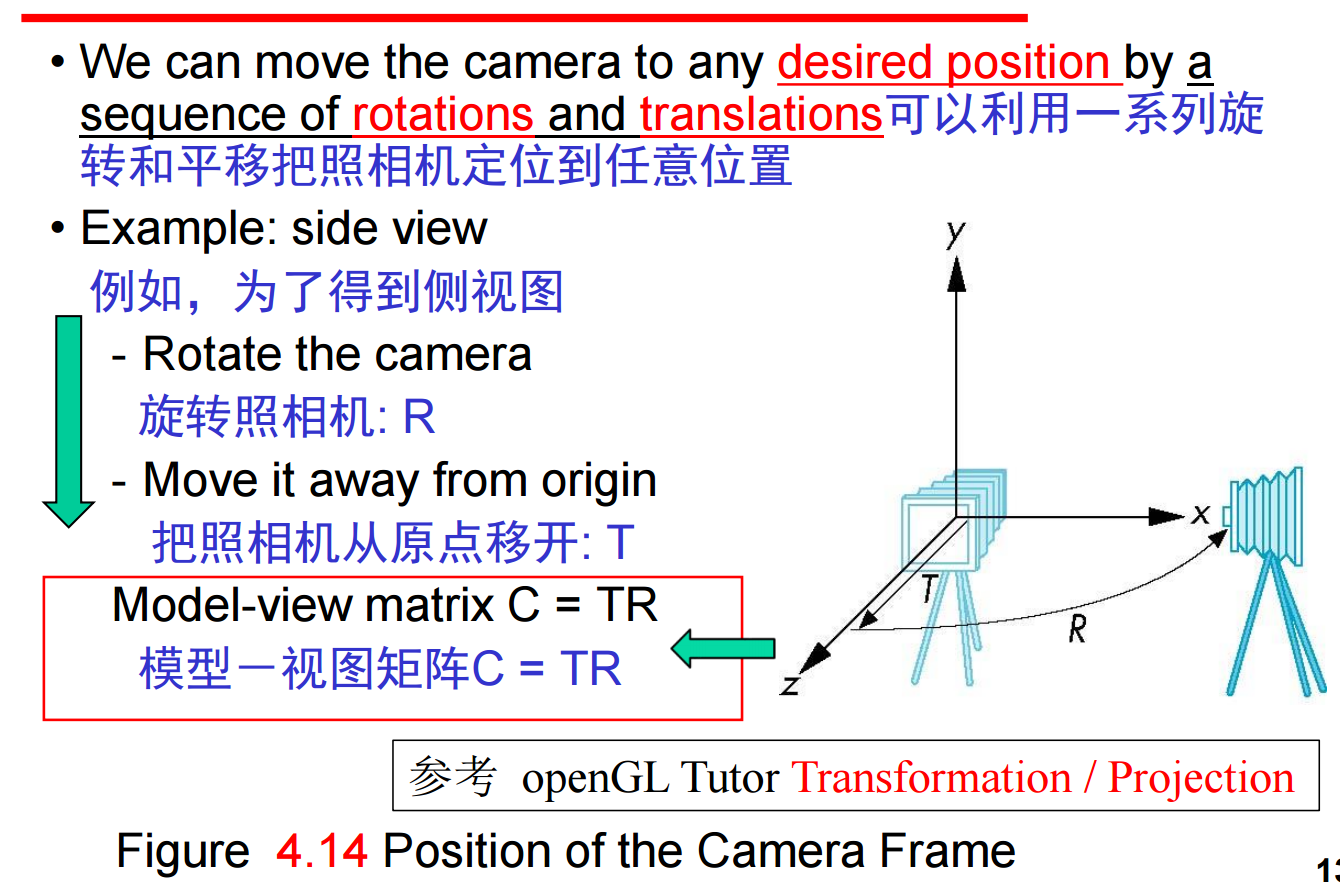
注意最后指定的变换是最先被应用的变换:
glMatrixMode(GL_MODELVIEW)
glLoadIdentity();
glTranslatef(0.0, 0.0, -d);
glRotatef(-90.0, 0.0, 1.0, 0.0);
如何理解该参数(正负值)?物理系统是对象不变,相机变;参数正负则从世界系统标架的角度来看对象的变化(所需要的变化)。这里的模型-视图矩阵是OpenGL状态的一部分——任何时刻的模型-视图矩阵包含了照相机标架与世界标架的位置关系,虽然表面上看把模型与视图矩阵结合为一个矩阵会导致一些混淆,但仔细体会这种流水线体系就会发现其中的优势。在世界物理标架中,把照相机也看作具有几何属性的对象,那么改变该对象位置和定向的变换,当然就会对照相机相对于其它对象的位置和定向也发生改变,可以认为在定义真正对象之前的模型-视图变换是定位照相机。

6、为了实现某种投影,需要经过复杂的计算得到变换的构成? 第一种方法,例如前面构造等角投影的方法。可以采用类似在PHIGS和GKS-3D中的方法定位照相机(在世界标架中描述照相机的位置、观察过程的第一部分),投影的类型是由在OpenGL中等价的投影矩阵确定的(指定投影变换矩阵、观察过程的第二部分、用标架的变换实现)。
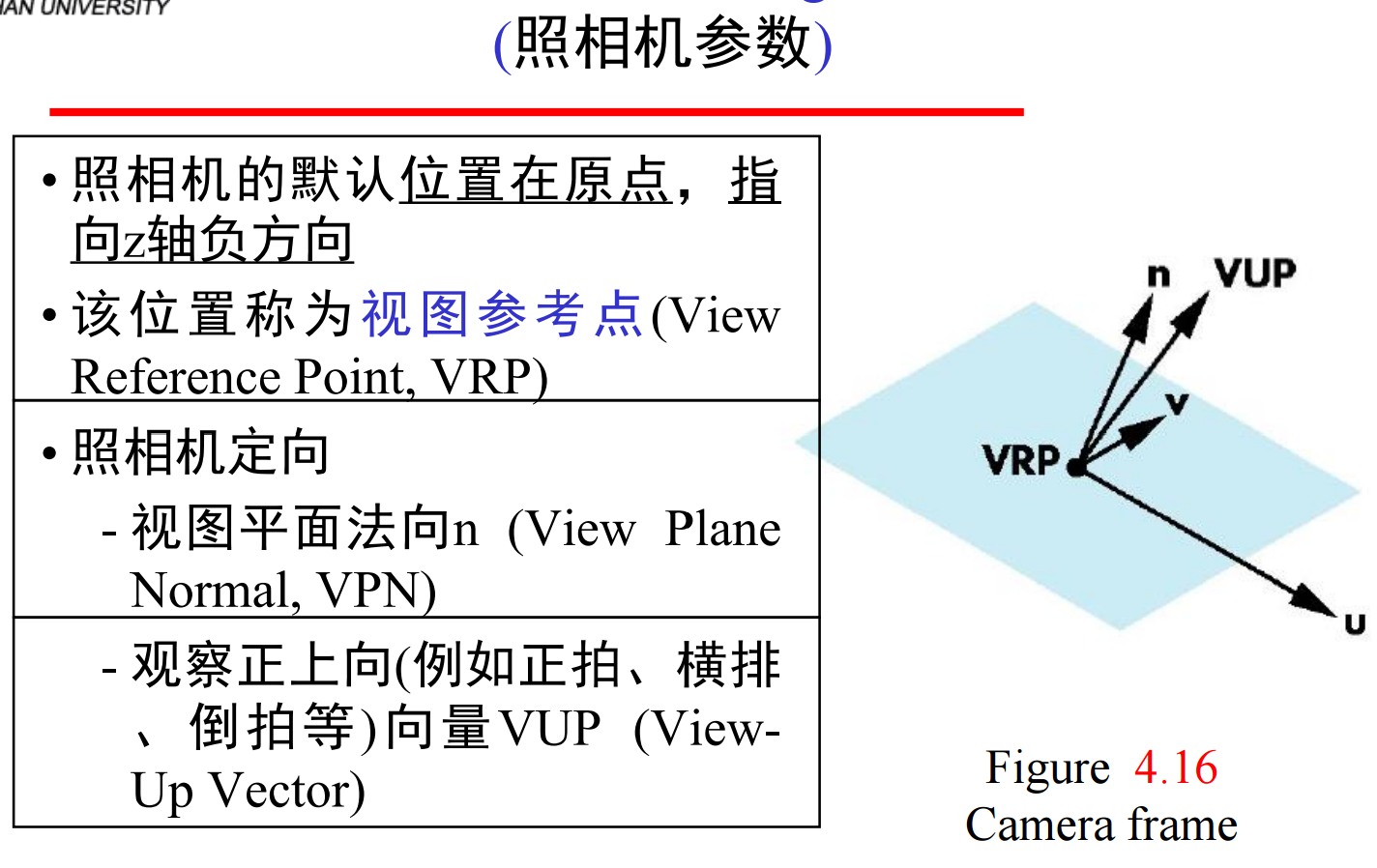
这里,VPN给出投影面的方向,即平面的法向。不过只有平面的定向,还不能完全确定照相机的定向,照相机还可以绕VPN方向旋转。只有给出了VUP观察正上向,才完全确定了照相机的方向。


7、GLU库函数gluLookAt(),提供定位照相机所用的模型-视图矩阵方法,注意在设置中需要一个向上的方向。这个函数需要初始化、即上载单位阵,也可以与模型变换复合在一起。例如:平行于轴的立方体的等角(等轴测图)投影:
glMatrixMode(GL_MODELVIEW):
glLoadIdentity();
gluLookAt(1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0. 0.0);
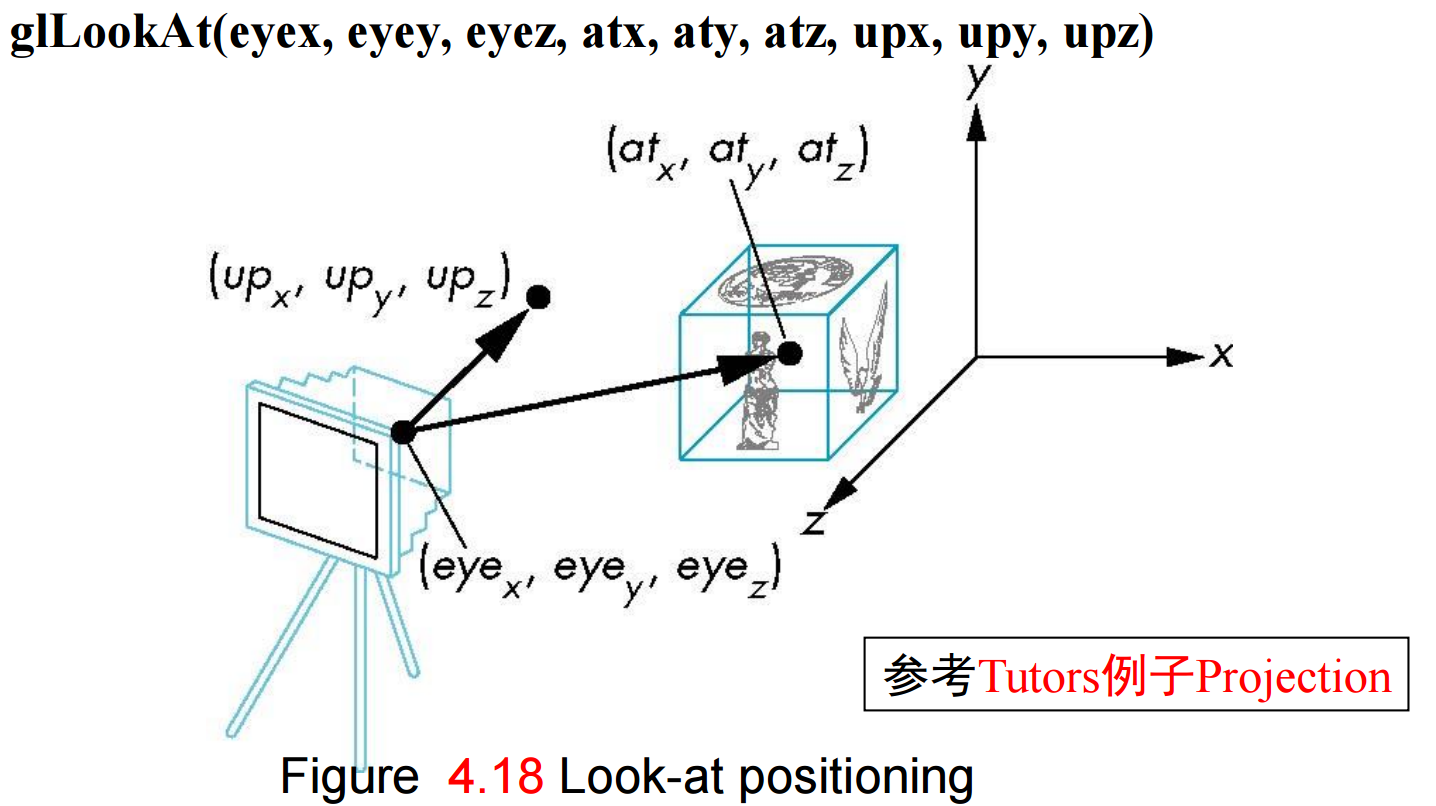
8、用户可以自己定义模型-视图矩阵实现同样的功能,但是从概念上可以把 gluLookAt() 作为照相机的定位,而把后续的其它变换作为对象的定位。注意,流水线执行矩阵计算,并不知道用户语义!在OpenGL中gluLookAt()函数是唯一的专门用来定位照相机的函数。但在许多实际应用中,已有的视图定义方法不适用,如飞机操纵模拟:
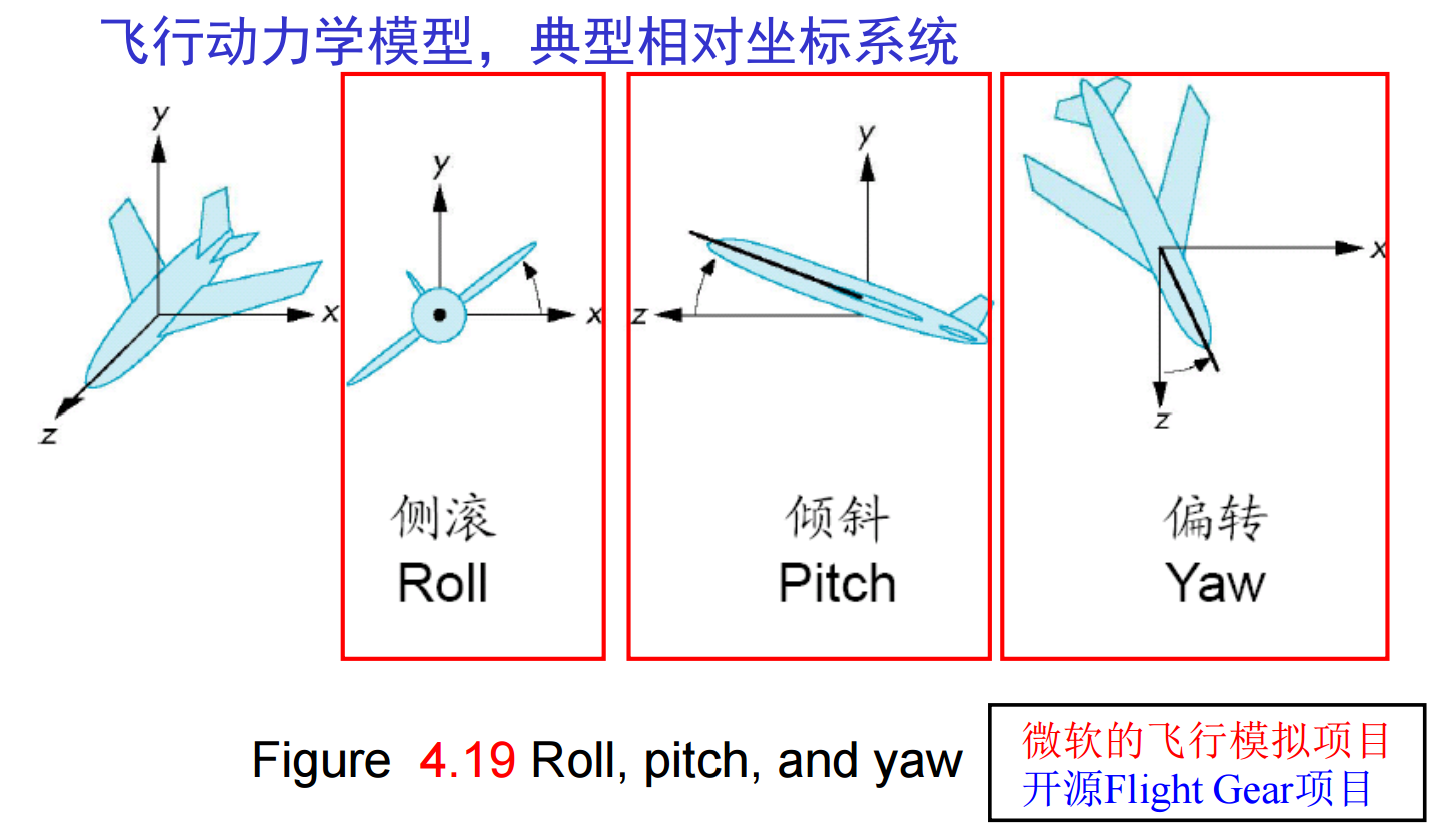
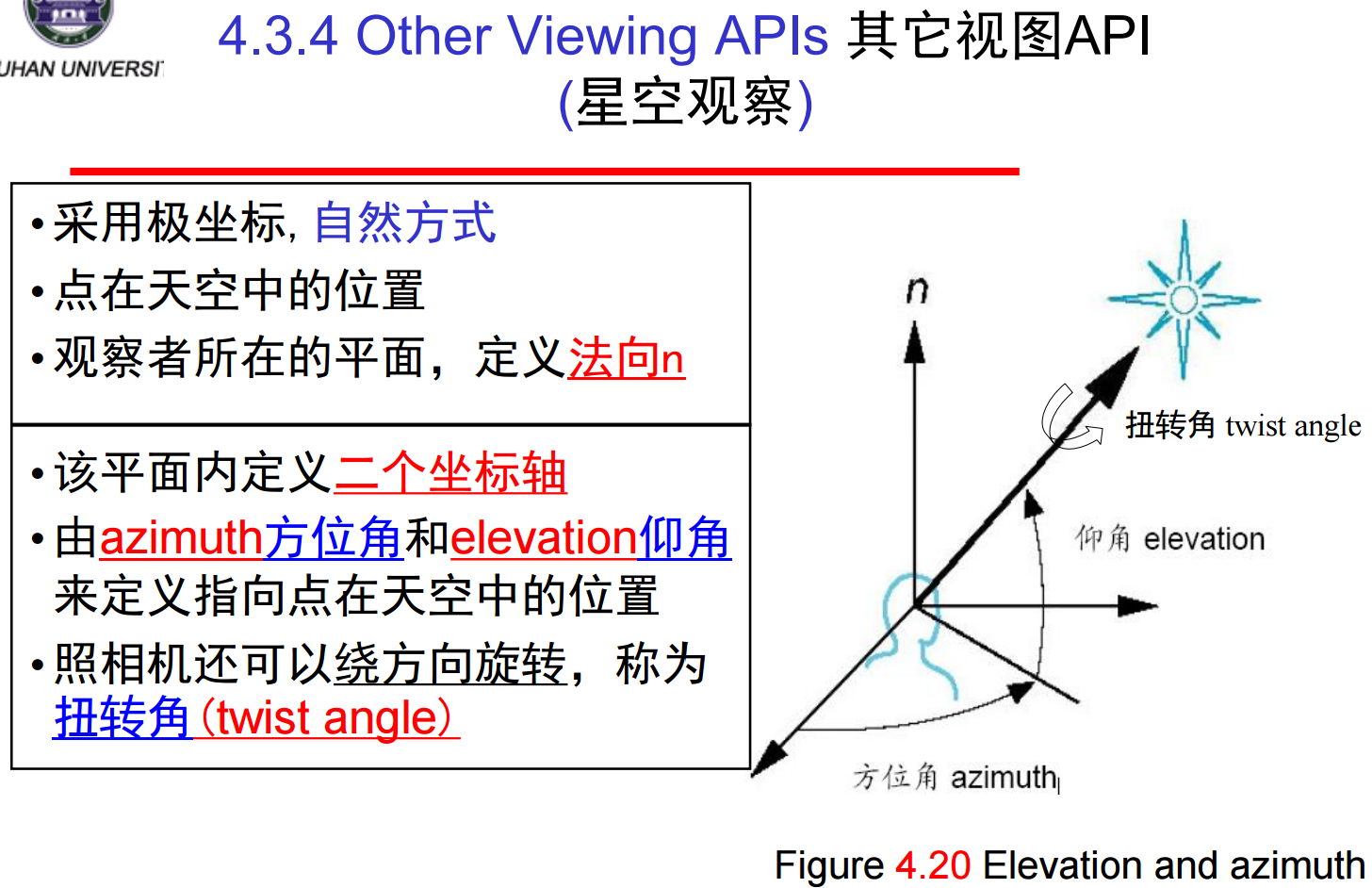
9、在物理照相机的简单投影中,物理照相机在定位后仍然可以选择镜头,镜头与胶卷的大小结合在一起确定在照相机前面多大范围的对象出现在最终的照片上;宽角镜头可以使离照相机近的对象看起来比离照相机远的对象夸张得大,类似透视投影的效果;远距镜头则会近似得到平行投影的效果。而在计算机中,可以选择投影的类型和视图参数来模拟镜头的远近;绝大多数API提供不同的函数用于定义平行投影和透视投影。OpenGL就是如此,虽然两者是在同一个流水线体系中实现——我们可以用glLoadMatrix设置投影矩阵:
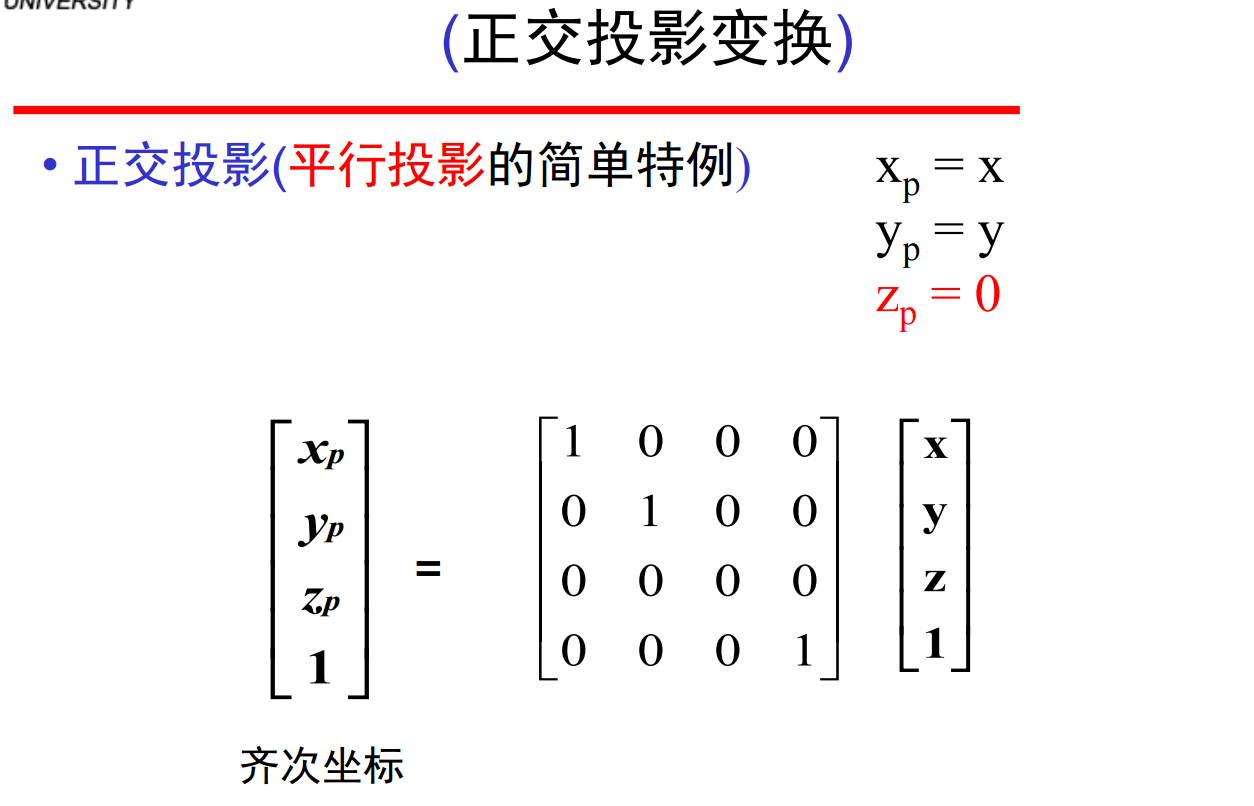

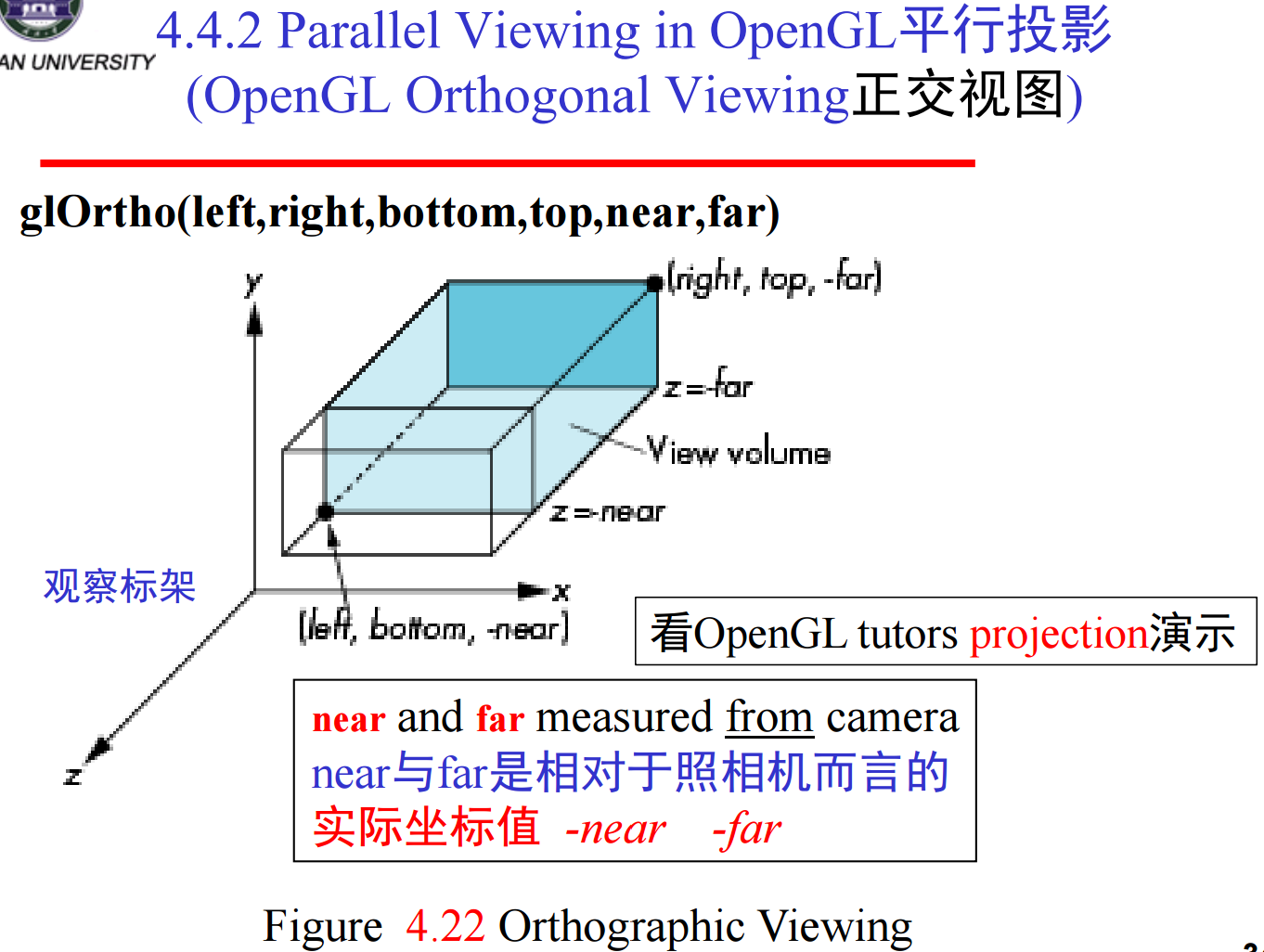
在视点(照相机)标架中默认的投影是正交投影。对于在默认视景体内的点,xp = x, yp = y, zp = 0。大多数图形系统应用视图规范化的过程是由投影矩阵确定的变换把所有其它的视图转化为默认视图,从而可以对所有的视图采用同样的流水线体系。
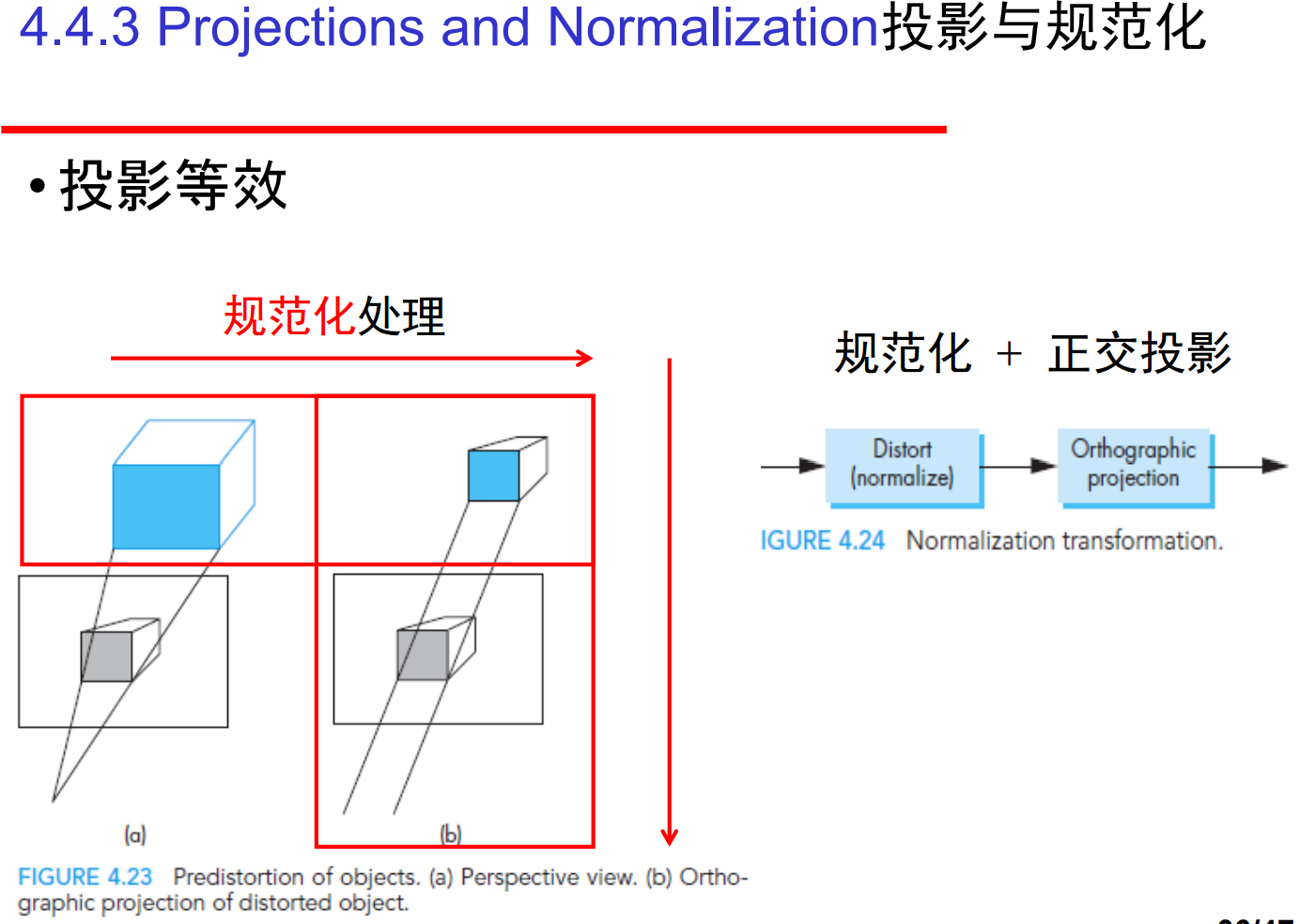
10、然后我们来看透视投影:
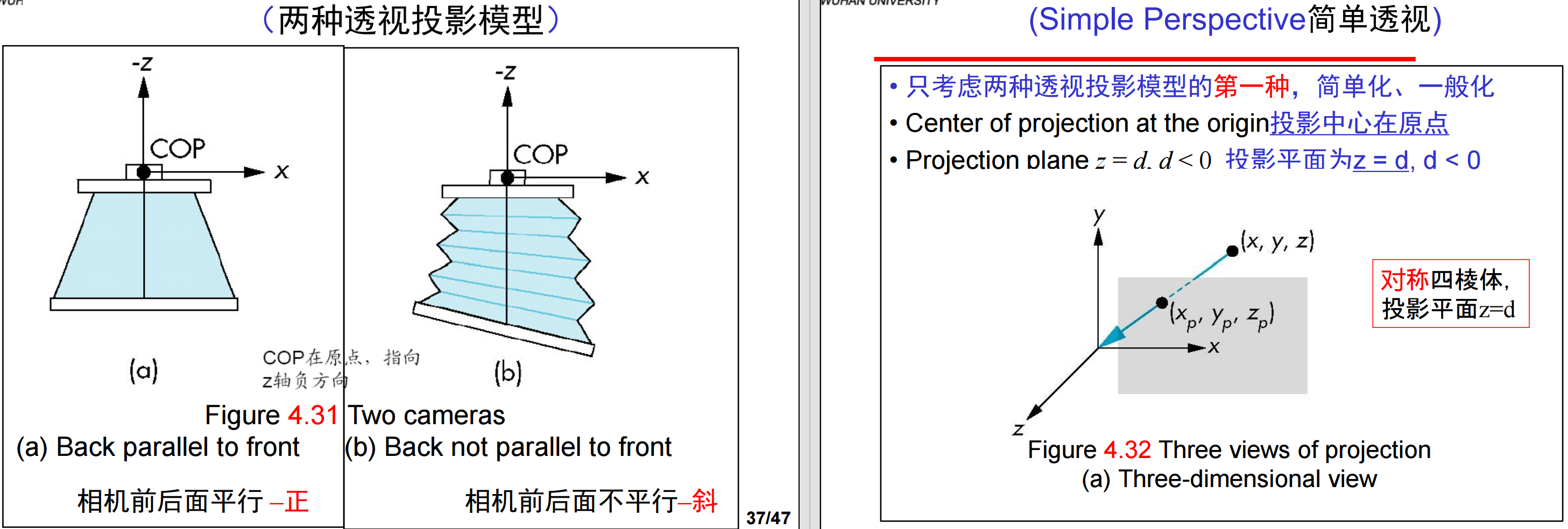
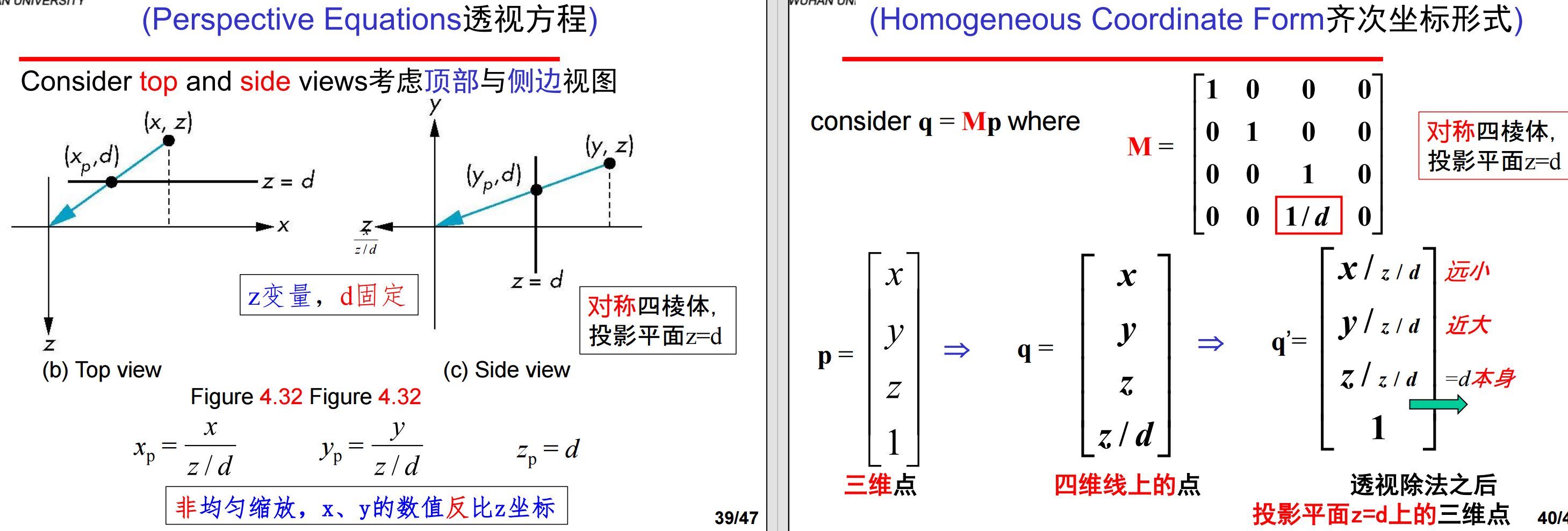
如果w = z/d ≠ 1, 那么必须从齐次坐标中除以w而得到所表示的点。这就是透视除法,结果为上述透视方程。不过,透视除法是非线性的,导致非均匀缩短 (non-uniform foreshortening)——线性方程,x方向仅与x变量有关(或者,y方向仅与y变量有关);非线性方程,多了一个1/z变量,还与z方向有关系;离COP更远的对象投影后尺寸比离COP近的对象更小。
这里,透视变换是保直线的,但不是仿射变换,不保持比例。即平行四边形 -> 平行四边形 = 仿射变换;平行四边形 -> 梯形 = 透视变换。而且,透视变换是不可逆(irreversible)的,因为沿一条投影直线上的所有点投影后的结果相同。
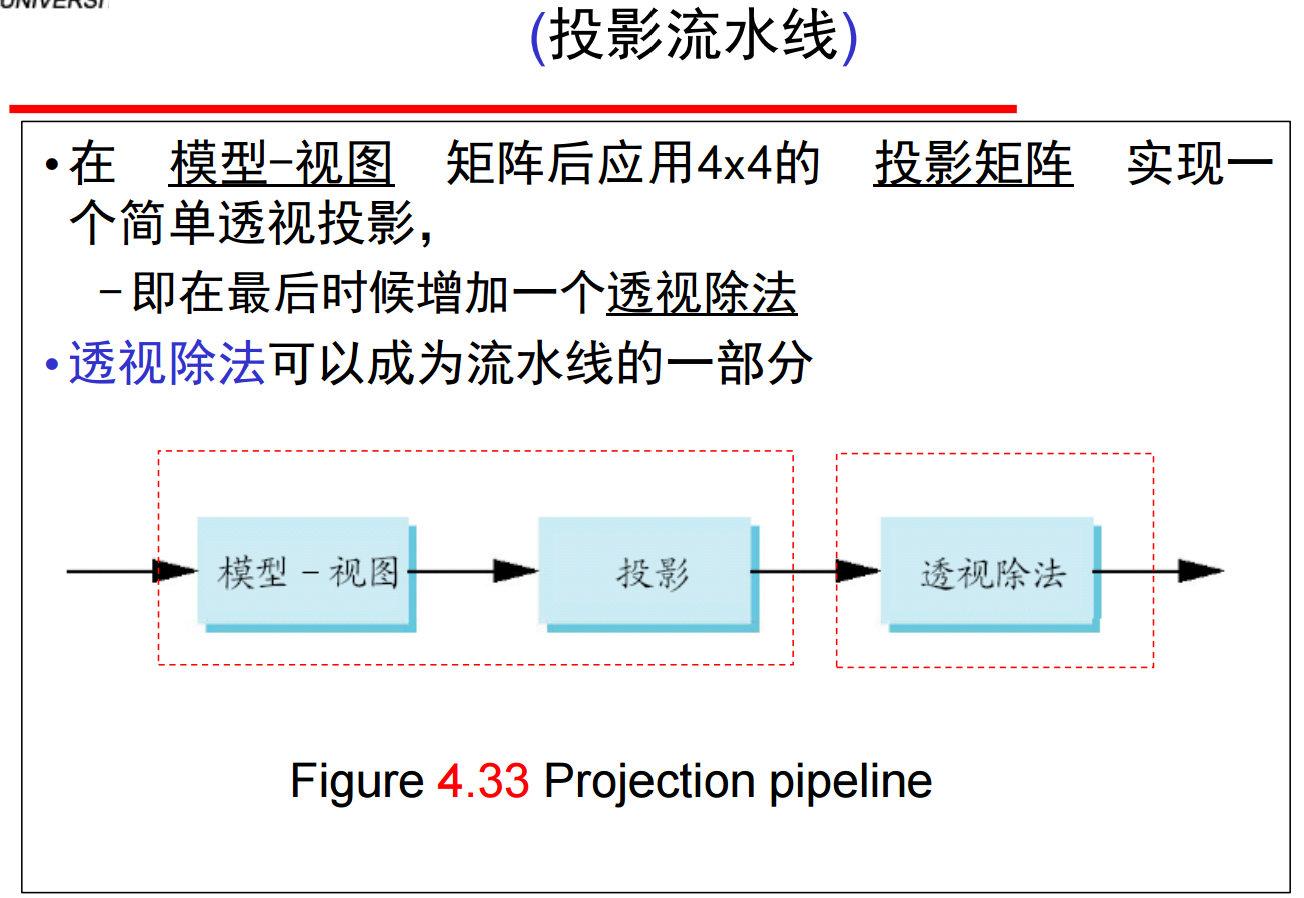
11、考虑OpenGL中的投影:
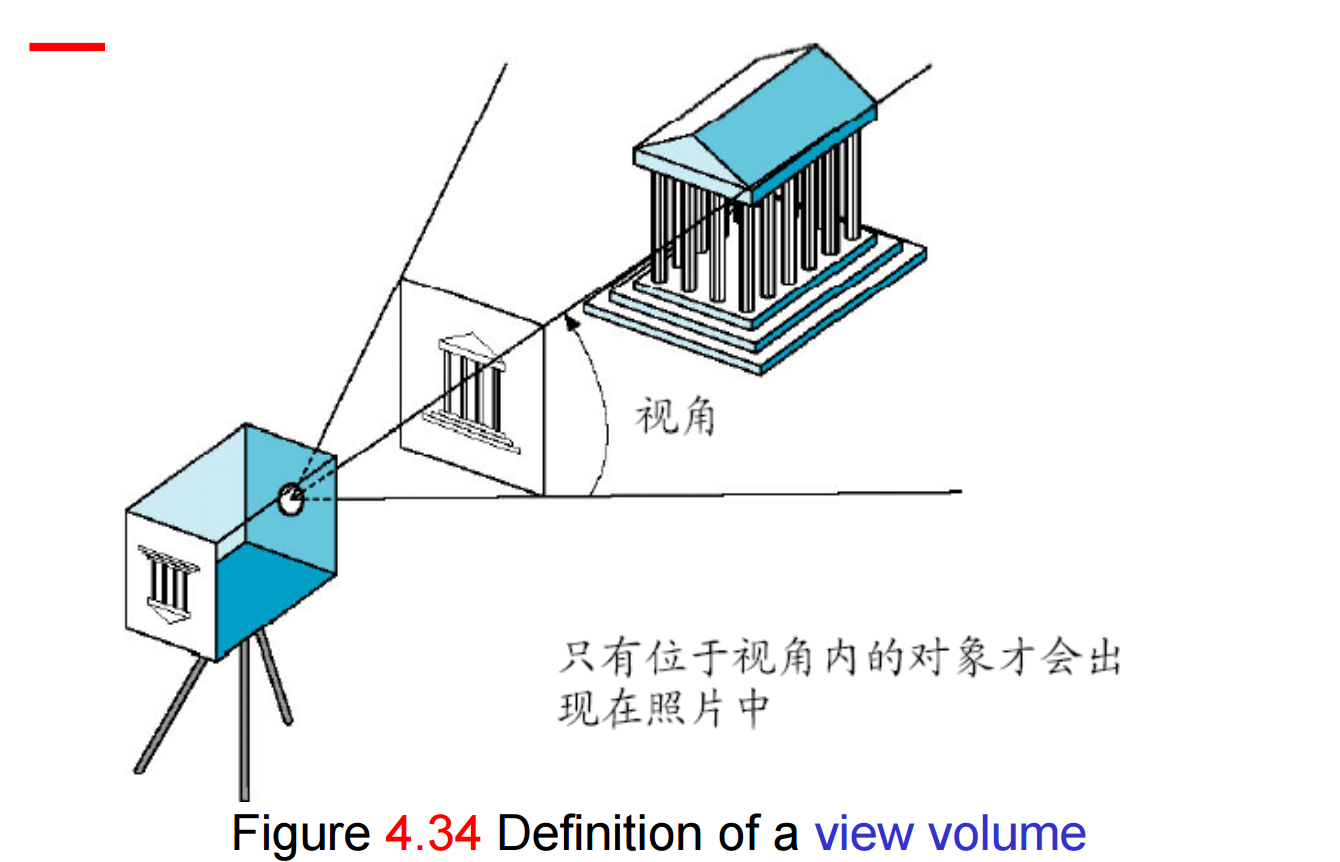
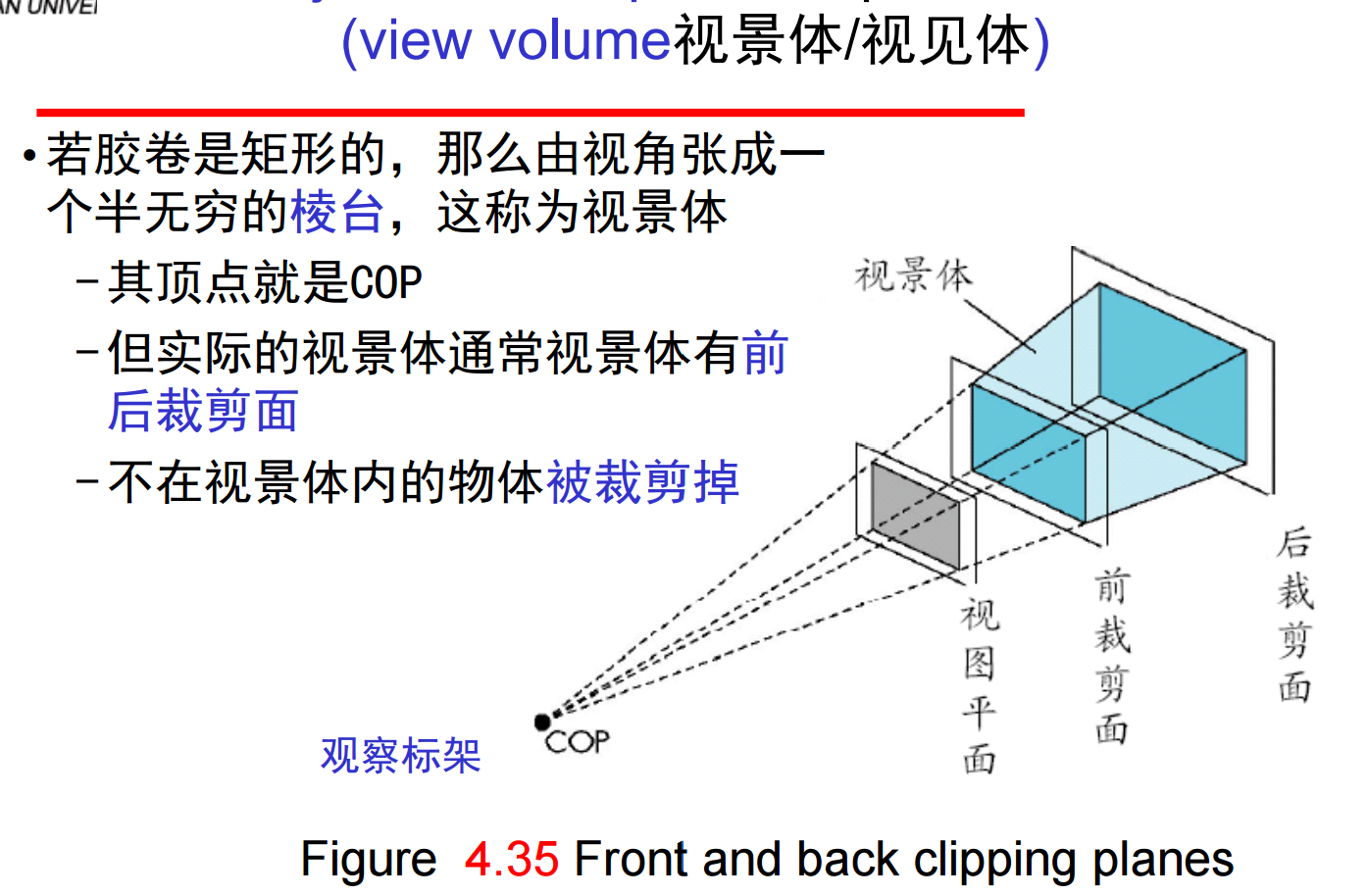
在绝大多数API中通过定义投影视景体确定裁剪参数。通过指定前、后裁剪面以及视角可以确定一个四棱体(frustum)作为视景体。在这个指定中有一个参数是固定的,即COP在原点(观察标架原点)。可以定义视景体的六个面差不多具有任意定向和位置,但这样很难确定视图,而且很少需要这种弹性。所以采用二个标准API来定义四棱体作为视景体:glFrustum 和gluPerpective。

