【高级机器学习】 13. 因果推断

因果推断

第一部分:因果思维(Causal Thinking)

1. 机器学习中的统计依赖性

机器学习系统通常由统计依赖性驱动。例如:

• 我们观察到"猫"和"狗"的图片在数据中经常一起出现
• 这种共现关系建立了统计上的依赖

关键问题:统计依赖不等于因果关系!

---

2. 经典案例:巧克力与诺贝尔奖

研究发现:国家的巧克力消费量与诺贝尔奖获得者数量呈正相关

问题:

• 这是否意味着吃巧克力能提高获得诺贝尔奖的概率?
• 显然不是!这里存在混淆因素(如国家的经济发展水平、教育投资等)

教训:相关性 ≠ 因果性

---

3. 咖啡与死亡率案例

初步发现:

• 喝咖啡的人死亡风险增加

深入分析:

• 喝咖啡的人更可能吸烟(混淆因素)

调整吸烟因素后:

• 咖啡摄入与死亡率呈现显著的负相关关系
• 也就是说,咖啡实际上可能降低死亡风险!

启示:必须控制混淆变量才能得到正确的因果结论

---

4. 辛普森悖论(Simpson’s Paradox)

定义:在分组数据中观察到的趋势,在合并数据后可能会逆转

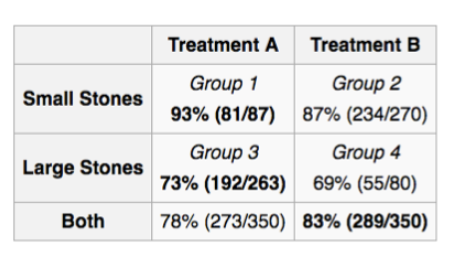
问题:

• 我们应该基于相关性做决策,还是基于其他东西?
• 答案:需要理解因果结构!

例子:

• 某药物在男性组和女性组中都显示负效果
• 但在总体数据中却显示正效果
• 这是因为性别是一个混淆变量

---

5. "奇怪"的依赖关系 - 大学录取案例

历史现象:

• 回到50年前,你可能会发现女大学生平均比男大学生更聪明

原因:

• 选择偏差(Selection Bias)!
• 当时女性上大学的门槛远高于男性
• 只有特别优秀的女性才能被录取
• 而男性录取标准相对宽松

教训:观察到的依赖关系可能是由选择机制造成的,而非真实的能力差异

---

第二部分:产生依赖关系的三种方式

1. 三种依赖机制

(1) 共同原因(Common Cause)

    Z↙ ↘X   Y

• Z同时影响X和Y
• X和Y之间产生依赖
• 例子:天气(Z)影响洒水器(X)和地面湿滑(Y)

(2) 因果关系(Causal Relation)

X → Y

• X直接导致Y
• 最直接的依赖关系

(3) 给定共同效应的条件依赖

  X   Y↘ ↙Z

• X和Y都影响Z
• 当我们观察到Z(conditioning on Z)时,X和Y之间会产生依赖
• 这称为对撞偏差(Collider Bias)

---

2. 因果关系 vs 依赖关系

核心区别:

• 依赖关系:统计上的相关性,双向的,对称的
• 因果关系:有方向性的,X导致Y ≠ Y导致X

重要性:

• 预测任务:依赖关系足够
• 干预决策:必须理解因果关系
• 反事实推理:必须理解因果关系

---

第三部分:因果表示

1. 有向无环图(DAG - Directed Acyclic Graph)

定义:

• 有向边的图
• 无环:不存在从某节点出发又回到该节点的路径

基本概念:

• 路径(Path):连接的顶点序列
• 例如:X₁ - X₂ - X₄ - X₅

DAG的作用:

• 用图形表示变量之间的因果关系
• 箭头方向表示因果方向:X → Y 表示 X 导致 Y

---

2. 马尔可夫条件(Markov Conditions)

目的:

• 马尔可夫条件说明:如果某个图属性成立,那么某个统计独立性就成立
• 连接图结构和概率分布

---

2.1 局部马尔可夫条件(Local Markov Condition)

定义:
在有向无环图中,每个变量Xᵢ在给定其父节点的条件下,独立于其非后代节点

数学表达:
$$(X_i\perp \perp Y|P{A}_i{)}_G⟹(X_i\perp \perp Y|P{A}_i{)}_p$$

X ⊥⊥ Y 表示：X 和 Y 统计独立

例子:

    X₁↙  ↘X₂  X₃↘  ↙X₄↓X₅

根据局部马尔可夫条件:

• $(X_4\perp \perp X_1|X_2,X_3{)}_G⟹(X_4\perp \perp X_1|X_2,X_3{)}_p$
• X₄在给定父节点X₂和X₃的条件下,独立于非后代X₁

马尔可夫条件保证：
既然图说它们独立，那么在概率分布中也独立

因果分解:
联合分布可以分解为:

P(X₁,...,X₅) = P(X₁)P(X₂|X₁)P(X₃|X₁)P(X₄|X₂,X₃)P(X₅|X₄)

每个变量只依赖于其父节点!

---

2.2 全局马尔可夫条件(D-分离)

定义:
对于三个不相交的变量集X、Y和S,如果所有从X到Y的路径都被S阻断,则称X被S d-分离于Y

路径被阻断的条件:

路径被集合S阻断,当且仅当:

1. 链结构(i → m → j)或叉结构(i ← m → j):

   • 中间节点m 在S中

2. 对撞结构(i → m ← j):

   • 中间节点m 不在S中
   • 且m的后代也不在S中

数学表达:

$(X\perp \perp Y|S{)}_G⟹(X\perp \perp Y|S{)}_p$

---

例子分析:

使用上面的图:

    X₁↙  ↘X₂  X₃↘  ↙X₄↓X₅

情况1:

• X = {X₁}, Y = {X₄, X₅}, S = {X₂, X₃}
• X₁到X₄的所有路径都经过X₂或X₃(叉结构)
• 条件化S后,这些路径被阻断
• 结论:X 被S d-分离于Y

情况2:

• X = {X₂}, Y = {X₃}, S = {X₁, X₄}
• X₂ → X₄ ← X₃ 是对撞结构
• X₄在S中,所以这条路径未被阻断
• 结论:X 不被S d-分离于Y

情况3:

• X = {X₂}, Y = {X₃}, S = {X₁}
• 对撞节点X₄不在S中,路径被阻断
• 结论:X 被S d-分离于Y

---

3. 因果忠实性假设(Causal Faithfulness Assumption)

问题:

• 概率分布可能有额外的条件独立关系,这些关系不是由图的d-分离蕴含的

忠实性定义:
如果分布中的条件独立关系仅由图的d-分离蕴含,则称分布对图是忠实的

数学表达:

$(X\perp \perp Y|S{)}_p⟹(X\perp \perp Y|S{)}_G$

不忠实的例子:

X = Uₓ
Y = αX + Uᵧ
Z = βX + γY + Uᵤ

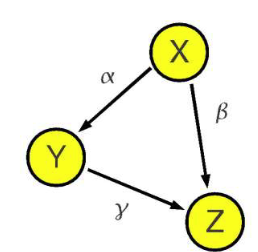
• 从图G看:$(X/\perp \perp Z{)}_G$ (X和Z不独立)
• 但如果 β + αγ = 0,则在分布p中:$(X\perp \perp Z{)}_p$
• 这是参数的巧合抵消,导致不忠实

实践中的假设:
我们通常假设分布是忠实的,这是一个合理的假设,因为参数巧合抵消的概率极低

---

第四部分:因果贝叶斯网络

1. 因果贝叶斯网络定义

特点:

• 有向边表示因果方向
• 构成因果DAG
• 更有意义,能表示外部变化(干预)的效果

与普通贝叶斯网络的区别:

• 普通贝叶斯网络:仅表示概率依赖
• 因果贝叶斯网络:边有因果解释

---

2. 三种推理层次

(1) 条件化/预测(Conditioning/Prediction)

P(slippery | Sprinkler = off)

• 问题:如果我们观察到洒水器关闭,地面会湿滑吗?
• 这是被动观察

(2) 干预(Intervention)

P(slippery | do(Sprinkler = off))

• 问题:如果我们主动关闭洒水器,地面会湿滑吗?
• 这是主动操作
• 使用 do算子表示干预

(3) 反事实推理(Counterfactual)

P(slippery_sprinkler=off | Sprinkler = on, Slippery = no)

• 问题:给定洒水器实际开着且地面不滑,如果当时洒水器关着,地面会滑吗?
• 这是对已发生事件的假设性推理

---

关键区别示例:

考虑下雨、洒水器和地面湿滑的关系:

     雨↙  ↘
洒水器  湿滑↘  ↙

• 条件化:观察到洒水器关闭 → 推断可能在下雨 → 地面可能仍然湿滑
• 干预:我们关闭洒水器 → 切断了雨→洒水器的路径 → 地面湿滑仅取决于雨

---

第五部分:因果效应的识别

1. 黄金标准:随机对照实验(RCT)

原理:

• 所有影响结果变量的其他因素都被固定或随机变化
• 因此结果变量的任何变化必定是由控制变量引起的

问题:

• 通常昂贵或不可行
• 例如:无法随机分配人们吸烟来研究吸烟对健康的影响

目标:
从观察性数据中估计因果效应,如:

P(Recovery | do(Treatment = A))

---

2. 干预 vs 条件化

例子:治疗(T)、性别(S)、康复®

图结构:

S → T → R↘     ↗

条件化:

P(R|T) = Σₛ P(R|T,S)P(S|T)

• 观察到治疗T时性别的分布

干预:

P(R|do(T)) = Σₛ P(R|T,S)P(S)

• 干预治疗T时,切断S→T的边
• 使用性别的边际分布P(S),而非条件分布P(S|T)

为什么不同?

• 条件化:S和T可能相关(例如某种治疗更常用于某性别)
• 干预:我们强制设置T,打破了自然的依赖关系

---

3. 后门准则(Back-Door Criterion)

定义:
给定因果图G,集合S满足相对于(X,Y)的后门准则,如果:

1. S中没有X的后代
2. S 阻断了X和Y之间所有包含指向X的箭头的路径

作用:
如果S满足后门准则,则:

P(Y|do(X)) = Σₛ P(Y|X,S)P(S)

直观理解:

• “后门路径”:从X到Y的路径中,有箭头指向X的路径
• 这些路径代表混淆(confounding)
• 后门准则要求找到一组变量S来阻断所有混淆路径

---

应用例子:

    S↙ ↘T   R↘ ↙

治疗-康复关系:

• S(性别)满足后门准则
• 通过调整S,可以估计治疗的因果效应:

P(R|do(T)) = Σₛ P(R|T,S)P(S)

---

4. 前门准则(Front-Door Criterion)

应用场景:
当存在未观测混淆时,后门准则失效,但前门准则可能适用

定义:
给定因果图G,集合M满足相对于(X,Y)的前门准则,如果:

1. M 完全中介了X对Y的所有因果效应(X到Y的所有路径都经过M)
2. X和M之间没有后门路径(无混淆)
3. 所有M到Y的后门路径都被X阻断

因果效应计算:

$P(Y|do(X))={\Sigma }_{m}P(M|X){\Sigma }_x^{\prime }P(Y|M,X^{\prime })P(X^{\prime })$

---

经典例子:吸烟与肺癌

  U(基因)↙     ↘
吸烟 → 焦油 → 肺癌

• U是未观测的混淆因素(如基因倾向)
• 焦油(M)是中介变量
• 焦油满足前门准则!

计算:

$P(肺癌|do(吸烟))={\Sigma }_{焦}油P(焦油|吸烟){\Sigma }_{吸}{烟}^{\prime }P(肺癌|焦油,吸{烟}^{\prime })P(吸{烟}^{\prime })$

即使不观测U,也能估计吸烟的因果效应!

---

第六部分:因果推断总结

1. 因果推断框架

完整流程:

观察数据 → 因果发现 → 因果图 → 因果效应识别 → 因果效应估计

1. 因果发现:从观察数据学习因果图结构
2. 因果识别:给定因果图,判断能否从观察数据计算因果效应
3. 因果估计:实际计算因果效应的数值

---

2. 因果发现(Causal Discovery)

核心问题:
能否仅从纯观察数据发现因果结构?

答案:

• 在某些假设下(忠实性、充分性等),可以!
• 但通常只能恢复到等价类(Markov等价类)
• 需要更多假设(如线性、非高斯等)才能唯一确定

方法类别:

1. 基于约束的方法:利用条件独立性测试(如PC算法)
2. 基于评分的方法:搜索最佳拟合数据的图结构
3. 基于函数因果模型的方法:利用特殊的数据生成机制

---

3. 核心要点总结

关键原则:

1. ⚠️ 依赖性 ≠ 因果性!!!
2. ✓ 因果性在干预研究中至关重要
3. ✓ 给定因果图,因果效应可以从观察数据估计
4. ✓ 因果图可以从观察数据学习

实践建议:

• 不要仅凭相关性做决策
• 理解数据生成过程
• 识别混淆因素
• 在可能的情况下使用随机实验
• 谨慎使用观察性研究的因果结论

---

4. 因果推断的应用场景

医疗健康:

• 评估治疗效果
• 药物副作用分析

经济政策:

• 政策效果评估
• 经济干预的影响

机器学习:

• 公平性(消除歧视)
• 迁移学习(分布变化)
• 可解释AI

社会科学:

• 教育干预效果
• 社会项目评估

---

附录:重要概念速查

概念对比表

概念	定义	符号
条件化	被动观察	P(Y|X)
干预	主动操作	P(Y|do(X))
因果效应	干预导致的变化	P(Y|do(X=1)) - P(Y|do(X=0))
混淆	影响X和Y的共同原因	X ← U → Y
中介	X通过M影响Y	X → M → Y
对撞	X和Y共同影响M	X → M ← Y

图结构速查

三种基本结构:

1. 链:X → M → Y
2. 叉:X ← M → Y
3. 对撞:X → M ← Y

阻断规则:

• 链/叉:条件化中间节点 → 阻断
• 对撞:条件化中间节点 → 未阻断