磁共振成像原理（理论）29：反转恢复序列 (Inversion-Recovery Sequence)

反转恢复序列

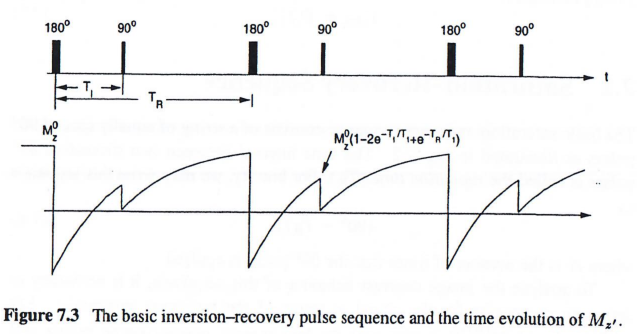
反转恢复是另一种常用的$T_1$加权成像序列，如图7.3所示。该序列以180°预备脉冲（反转脉冲）开始，简写为：
$$(180^{\circ }-T_I-90^{\circ }-T_D{)}_N\text{\hspace{1em}(7.20)}$$

其中$T_I$为反转时间，$T_D$为恢复时间。

第1次反转恢复：$0\le t<T_R$

在时间$t=0_{-}$时刻，系统处于热平衡状态，纵向磁化强度达到最大值：
$$M_z(0_{-})=M_z^0\text{\hspace{1em}()}$$

在$t=0$时刻施加180°射频脉冲，将纵向磁化强度完全反转：
$$M_z(0_{+})=-M_z^0\text{\hspace{1em}(A)}$$

在反转时间$T_I$内，纵向磁化强度按照$T_1$弛豫规律从$-M_z^0$向$M_z^0$恢复。根据弛豫方程（式3.122）
$$\{\begin{array}{l}{M}_{x^{\prime }{y}^{\prime }}(t)=M_{x^{\prime }{y}^{\prime }}(0_{+})e^{-t/T_2}\\ M_{z^{\prime }}(t)=M_z^0(1-e^{-t/T_1})+M_{z^{\prime }}(0_{+})e^{-t/T_1}\end{array}\text{\hspace{1em}(3.122)}$$

可得：
$$M_z(t)=M_z^0\left(1-2e^{-t/T_1}\right)(0<t<T_I)\text{\hspace{1em}()}$$

在$t=T_{I-}$时刻，即90°脉冲施加前，纵向磁化强度为：
$$M_z(T_I-)=M_z^0\left(1-2e^{-T_I/T_1}\right)\text{\hspace{1em}()}$$

在$t=T_I$时刻施加90°射频脉冲，将此时的纵向磁化强度翻转到横向平面。对于理想的90°脉冲，在$t=T_{I+}$横向磁化强度为：
$$M_{xy}(T_I+)=M_z(T_I-)=M_z^0\left(1-2e^{-T_I/T_1}\right)\text{\hspace{1em}(B)}$$

第2次反转恢复：$T_R\le t<2T_R$

在实际成像序列中，我们需要考虑完整的重复周期$T_R=T_I+T_D$。在延迟时间$T_D$内，纵向磁化强度继续恢复。

在$t={T_R}_{-}$时刻，即第二个180°脉冲施加前，纵向磁化强度为：
$$M_z(T_R-)=M_z^0\left(1-e^{-T_D/T_1}\right)\text{\hspace{1em}()}$$

第二个180°脉冲将其反转为：
$$M_z(T_R+)=-M_z^0\left(1-e^{-T_D/T_1}\right)\text{\hspace{1em}(C)}$$

*注意：式子A和式子C分别是第一次180°脉冲和第二次180°脉冲施加后的纵向磁化强度，两者是不一样的。

在$t=(T_R+T_I{)}_{-}$时刻，即第二个90°脉冲施加前，纵向磁化强度为：
$$\begin{array}{rl}{M}_z((T_R+T_I{)}_{-})& =M_z^0(1-e^{-T_I/T_1})+M_{z^{\prime }}(T_{R+})e^{-T_I/T_1}\\ & =M_z^0(1-e^{-T_I/T_1})-M_z^0\left(1-e^{-T_D/T_1}\right)e^{-T_I/T_1}\\ & =M_z^0(1-2e^{-T_I/T_1})-M_z^0+e^{-(T_D+T_I)/T_1}\\ & =M_z^0(1-2e^{-T_I/T_1})+M_z^0{e}^{-T_R/T_1}\end{array}\text{\hspace{1em}()}$$

在$t=(T_R+T_I{)}_{+}$时刻，即第二个90°脉冲施加后，横向磁化强度为：
$$M_{xy}((T_R+T_I{)}_{+})=M_z((T_R+T_I{)}_{-})=M_z^0(1-2e^{-T_I/T_1})+M_z^0{e}^{-T_R/T_1}\text{\hspace{1em}(D)}$$

*注意：式子B和式子D分别是第一次90°脉冲和第二次90°脉冲施加后的横向磁化强度，两者是不一样的。

第3次反转恢复：$2T_R\le t<3T_R$

在$t={2T_R}_{-}$时刻，即第三个180°脉冲施加前，纵向磁化强度为：
$$M_z(2T_R-)=M_z^0\left(1-e^{-T_D/T_1}\right)\text{\hspace{1em}()}$$

第三个180°脉冲将其反转为：
$$M_z(2T_R+)=-M_z^0\left(1-e^{-T_D/T_1}\right)\text{\hspace{1em}(E)}$$

*注意：式子C和式子E分别是第二次180°脉冲和第三次180°脉冲施加后的纵向磁化强度，两者是一样的，重复开始出现。

在$t=(2T_R+T_I{)}_{-}$时刻，即第三个90°脉冲施加前，纵向磁化强度为：
$$\begin{array}{rl}{M}_z((2T_R+T_I{)}_{-})& =M_z^0(1-e^{-T_I/T_1})+M_{z^{\prime }}(2T_{R+})e^{-T_I/T_1}\\ & =M_z^0(1-e^{-T_I/T_1})-M_z^0\left(1-e^{-T_D/T_1}\right)e^{-T_I/T_1}\\ & =M_z^0(1-2e^{-T_I/T_1})-M_z^0+e^{-(T_D+T_I)/T_1}\\ & =M_z^0(1-2e^{-T_I/T_1})+M_z^0{e}^{-T_R/T_1}\end{array}\text{\hspace{1em}()}$$

在$t=(2T_R+T_I{)}_{+}$时刻，即第三个90°脉冲施加后，横向磁化强度为：
$$M_{xy}((2T_R+T_I{)}_{+})=M_z((2T_R+T_I{)}_{-})=M_z^0(1-2e^{-T_I/T_1})+M_z^0{e}^{-T_R/T_1}\text{\hspace{1em}(F)}$$

*注意：式子D和式子F分别是第二次90°脉冲和第三次90°脉冲施加后的横向磁化强度，两者是一样的，重复开始出现。

因此，我们抛弃第一次循环的数据，从第二次开始采集。

图像强度作为$T_1$弛豫时间和脉冲定时参数的函数可表示为：
$$I(\mathbf{r})\propto \rho (\mathbf{r})\left[1-2e^{-T_I/T_1(\mathbf{r})}+e^{-T_R/T_1(\mathbf{r})}\right]\text{\hspace{1em}(7.21)}$$

应用举例

为了加强不同组织之间的对比度，必须使得其中一个组织信号为零，即 $I(\mathbf{r})=0$，由于自旋密度 $\rho (\mathbf{r})\ne 0$，必须有：
$$1-2e^{-T_I/T_1(\mathbf{r})}+e^{-T_R/T_1(\mathbf{r})}=0\text{\hspace{1em}(1)}$$

特别地，对于 $T_1(\mathbf{r})=T_1^0$ 的组织，条件变为：
$$1-2e^{-T_I/T_1^0}+e^{-T_R/T_1^0}=0\text{\hspace{1em}(2)}$$
与饱和恢复序列相比，反转恢复序列可通过调整$T_I$和$T_R$两个参数优化$T_1$对比度。特别地，通过合理选择$T_I$可使某些组织成分呈负强度甚至零强度。

例如，设$T_I$为：
$$T_I=\left[\ln 2-\ln (1+e^{-T_R/T_1^0})\right]T_1^0\text{\hspace{1em}(7.22)}$$

将式(7.22)中的 $T_I$ 表达式代入指数项 $e^{-T_I/T_1^0}$：
$$e^{-T_I/T_1^0}=e^{-\frac{1}{T_1^0}\cdot \left[\ln 2-\ln \left(1+e^{-T_R/T_1^0}\right)\right]T_1^0}\text{\hspace{1em}(3)}$$

由于 $T_1^0$ 在分子和分母中抵消，上式简化为：
$$e^{-T_I/T_1^0}=e^{-\left[\ln 2-\ln \left(1+e^{-T_R/T_1^0}\right)\right]}\text{\hspace{1em}(4)}$$

应用指数函数的性质 $e^{-(a-b)}=e^{-a}\cdot e^b$，得：
$$e^{-T_I/T_1^0}=e^{-\ln 2}\cdot e^{\ln \left(1+e^{-T_R/T_1^0}\right)}\text{\hspace{1em}(5)}$$

利用对数恒等式 $e^{\ln x}=x$ 和 $e^{-\ln 2}=\frac{1}{2}$，可得：
$$e^{-T_I/T_1^0}=\frac{1}{2}\cdot \left(1+e^{-T_R/T_1^0}\right)\text{\hspace{1em}(6)}$$

将结果(6)代入信号表达式(2)：
$$1-2\cdot \left[\frac{1}{2}\cdot \left(1+e^{-T_R/T_1^0}\right)\right]+e^{-T_R/T_1^0}=0\text{\hspace{1em}(7)}$$

展开计算：
$$1-\left(1+e^{-T_R/T_1^0}\right)+e^{-T_R/T_1^0}=1-1-e^{-T_R/T_1^0}+e^{-T_R/T_1^0}=0\text{\hspace{1em}(8)}$$

由此证明，当 $T_I$ 取公式(7.22)的值时，确实有：
$$1-2e^{-T_I/T_1^0}+e^{-T_R/T_1^0}=0\text{\hspace{1em}(7.23)}$$

此时，任何$T_1=T_1^0$的组织成分在最终图像中无信号贡献，称为信号抵消效应。该特性使反转恢复序列能产生比饱和恢复序列更强的$T_1$对比度，特别适用于区分自旋密度和$T_2$值相似但$T_1$值略有差异的组织。