磁共振成像原理（理论）33：图像噪声 (Image Noise)

本专题主要参考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 8.2

成像涉及对物体激活信号的测量和处理。任何实际测量均包含一个与期望信号不相关的非期望成分，该成分被称为噪声或随机信号。噪声在成像系统中的产生通常源于自发波动，例如实际电子元件内部自由电子的热运动（如电阻所表现出来的热噪声）。成像重点关注的核心问题是：噪声如何在成像系统中被拾取或产生，以及成像过程如何处理噪声——即噪声是被抑制还是被放大。

该问题的第一个方面主要涉及成像系统硬件，本文不作讨论（在完成整个理论部分后，我们再实际开始推导）。感兴趣的读者可参阅Chen和Hoult的专著获取精彩论述（后面写部件的指标对成像影响的时候再好好找找）

第二个方面涉及图像形成所采用的数学和处理原理，本节将对此展开讨论。我们首先回顾噪声信号的一些基本概念和术语体系。

随机信号基本概念

随机变量

在磁共振成像中，噪声信号的特征是在重复测量中不具有固定值(如下图右)。这类量在数学上用随机变量描述。随机变量的严格定义涉及样本空间上的函数关系，但为简化理解，可将其视为在特定测量中取值"任意"但遵循统计规律的量。

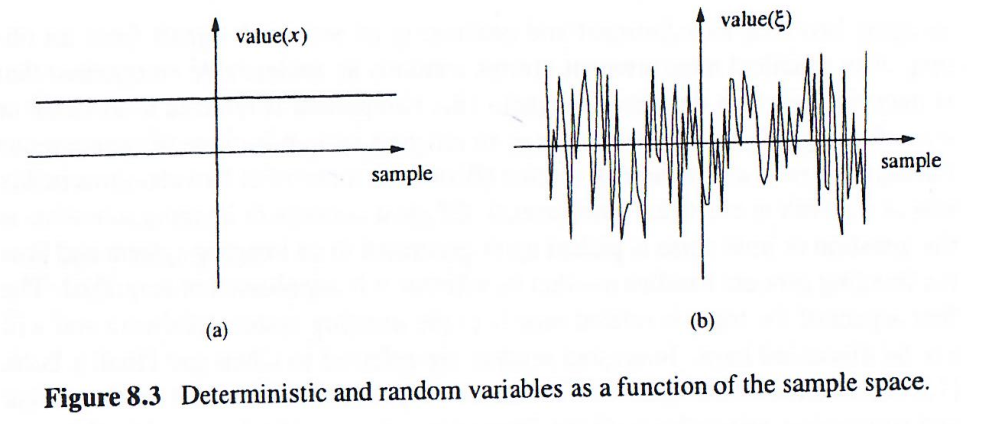
任何随机变量都完全由其概率密度函数（PDF） 描述。对于随机变量$\xi$，其PDF记为$p_{\xi }(x)$，表示在一次特定测量中获得值$x$的概率。由于实验总是会产生某个值，PDF曲线下的总面积必须为1：
$${\int }_{-\infty }^{\infty }{p}_{\xi }(x)dx=1\text{\hspace{1em}(8.20)}$$

在实践中，$p_{\xi }(x)$可呈现多种形式，如均匀分布或高斯分布，分别对应均匀噪声或高斯噪声。虽然随机变量完全由其PDF表征，但在实际应用中往往无法获知完整的PDF信息，因此通常使用均值和方差等参数进行描述。

均值是随机变量的PDF加权平均值，也称为集合平均值或数学期望值。对于连续随机变量：
ξˉ=E{ξ}=∫−∞∞xpξ(x)dx(8.21)\bar{\xi} = E\{\xi\} = \int_{-\infty}^{\infty} x p_{\xi}(x) dx \tag{8.21} ξˉ​=E{ξ}=∫−∞∞​xpξ​(x)dx(8.21)

对于离散随机变量：
ξˉ=E{ξ}=∑mxmpξ(xm)(8.22)\bar{\xi} = E\{\xi\} = \sum_{m} x_m p_{\xi}(x_m) \tag{8.22} ξˉ​=E{ξ}=m∑​xm​pξ​(xm​)(8.22)

其中$E$表示数学期望算子。它表示集平均，均值是一阶统计矩，仅涉及随机变量的一次幂。

什么是集平均？

感觉它就是一个理想实验，下面是不严谨的通俗解释

假设相同的试验、在同一时刻、在不同的地方、被多次（无数次）、且独立的执行，这个时候所有可能的“结果“都会被遍历。然后根据每一个结果（事件）的次数和所有事件的总数之比来计算事件的概率，以及他的数学期望值。因此，我们说期望值是一个集合平均值。拿扔硬币举例，想象下，在某个时刻，全世界所有人，都向上扔一个相同的硬币，而且力道等因素都一模一样，然后去检测每个硬币的朝向结果。

方差是二阶统计矩，衡量随机变量偏离其均值的程度：
σξ2=var{ξ}=E{(ξ−ξˉ)(ξ−ξˉ)∗}(8.23)\sigma_{\xi}^{2} = \text{var}\{\xi\} = E\{(\xi - \bar{\xi})(\xi - \bar{\xi})^{*}\} \tag{8.23} σξ2​=var{ξ}=E{(ξ−ξˉ​)(ξ−ξˉ​)∗}(8.23)

方差的正平方根${\sigma }_{\xi }$称为标准差，是偏离均值的平均偏差的度量。

示例1： 扔硬币

举例子：扔硬件猜正反面（排除硬币裂开，或者立起来），用$x=0,x=1$ 分别表示硬币出现正面朝上，和反面朝上这两个观测结果。在某一个时刻，无数个地方同时且相互独立的都做了这么个扔硬币试验，那么去统计这些地方的实验结果，可以计算出来正反面出现的概率都是50%，即
$${\int }_{-\infty }^{\infty }{p}_{\xi }(x)dx=p_{\xi }(0)+p_{\xi }(1)=50\%+50\%=1$$

其均值为0.5：
ξˉ=E{ξ}=∑mxmpξ(xm)=0⋅50%+1⋅50%=0.5\bar{\xi} = E\{\xi\} = \sum_{m} x_m p_{\xi}(x_m) = 0 \cdot 50\% + 1\cdot50\% = 0.5 ξˉ​=E{ξ}=m∑​xm​pξ​(xm​)=0⋅50%+1⋅50%=0.5

其方差为0.25：
σξ2=var{ξ}=E{(ξ−ξˉ)(ξ−ξˉ)∗}=E{ξ2−2ξξˉ+ξˉ2}=E{ξ2}−2E{ξξˉ}+E{ξˉ2}=E{ξ2}−2ξˉE{ξ}+ξˉ2={02⋅50%+12⋅50%}−2⋅0.5⋅0.5+0.5⋅0.5=0.5−0.5+0.25=0.25\begin{aligned} \sigma_{\xi}^{2} &= \text{var}\{\xi\} = E\{(\xi - \bar{\xi})(\xi - \bar{\xi})^{*}\} \\ &=E\{\xi^2 - 2\xi\bar{\xi} + {\bar{\xi}}^2\}\\ &=E\{\xi^2\} - 2E\{\xi\bar{\xi}\} + E\{{\bar{\xi}}^2\}\\ &=E\{\xi^2\} - 2\bar{\xi}E\{\xi\} + {\bar{\xi}}^2\\ &=\{0^2\cdot50\%+1^2\cdot50\%\} - 2\cdot0.5\cdot0.5+0.5\cdot0.5 \\ &=0.5 -0.5+0.25=0.25 \end{aligned} σξ2​​=var{ξ}=E{(ξ−ξˉ​)(ξ−ξˉ​)∗}=E{ξ2−2ξξˉ​+ξˉ​2}=E{ξ2}−2E{ξξˉ​}+E{ξˉ​2}=E{ξ2}−2ξˉ​E{ξ}+ξˉ​2={02⋅50%+12⋅50%}−2⋅0.5⋅0.5+0.5⋅0.5=0.5−0.5+0.25=0.25​

注意，不是一个试验先后做无数次，而是无数个地方同时进行着相同的试验，后者是集平均，前者是时间平均，后面会介绍。两者在满足特定条件下可以等同。

示例2：均匀分布

假设 $\xi$ 是在区间 $(x_1,x_2)$ 上定义的均匀随机变量，则其概率密度函数为 $p_{\xi }(x)=1/(x_2-x_1)$。$\xi$ 的均值为：
$$\bar{\xi }={\int }_{-\infty }^{\infty }x{p}_{\xi }(x)dx=\frac{1}{x_2-x_1}{\int }_{x_1}^{x_2}xdx=\frac{x_1+x_2}{2}$$

其标准差为：
$$\begin{array}{rl}{\sigma }_{\xi }& =\sqrt{{\int }_{-\infty }^{\infty }(x-\bar{\xi }{)}^2{p}_{\xi }(x)dx}\\ & =\sqrt{\frac{1}{x_2-x_1}{\int }_{x_1}^{x_2}{\left(x-\frac{x_1+x_2}{2}\right)}^{2}dx}\\ & =\frac{1}{\sqrt{3}}\frac{x_2-x_1}{2}\end{array}$$

示例3：高斯分布

高斯随机变量的概率密度函数（PDF）为：
$$p_{\xi }(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-(x-\mu {)}^2/2{\sigma }^2}\text{\hspace{1em}(8.24)}$$

根据定义可以证明，$\bar{\xi }=\mu$ 且 ${\sigma }_{\xi }=\sigma$。

随机变量的统计关系

在磁共振成像中，噪声数据点或图像像素通常由大量随机变量表征。一个重要问题是：在经过傅里叶变换等数学运算后，重建图像的均值和方差如何变化？或者更简单地说，对两个相邻噪声像素进行平均后的噪声方差是多少？回答这些问题需要了解所涉及随机变量间的统计关系。

描述两个随机变量${\xi }_1$和${\xi }_2$之间统计关系的两个重要概念是统计独立性和不相关性。

如果同时获得${\xi }_1$的值$x$和${\xi }_2$的值$y$的概率等于各自概率的乘积：

$$p_{{\xi }_1{\xi }_2}(x,y)=p_{{\xi }_1}(x)p_{{\xi }_2}(y)\text{\hspace{1em}(8.25)}$$

则称${\xi }_1$和${\xi }_2$是统计独立的。统计独立性是非常强的条件，实际感兴趣的随机变量很少满足。

如果我们只关心二阶统计特性，两个随机变量的相互依赖性可以通过相关系数来评估：
$$c_{{\xi }_1{\xi }_2}=\frac{E\{({\xi }_1-{\bar{\xi }}_1)({\xi }_2-{\bar{\xi }}_2{)}^{\ast }\}}{{\sigma }_{{\xi }_1}{\sigma }_{{\xi }_2}}\text{\hspace{1em}(8.26)}$$

从定义可知，$-1\le c_{{\xi }_1{\xi }_2}\le 1$。当$c_{{\xi }_1{\xi }_2}=0$时，${\xi }_1$和${\xi }_2$称为不相关的；当$c_{{\xi }_1{\xi }_2}=\pm 1$时，它们具有线性依赖性。

不相关性只是二阶统计的度量，不相关的随机变量不一定独立，但独立的随机变量总是不相关的。例如，如果${\xi }_1$和${\xi }_2$独立，则：
$$\begin{array}{rl}{c}_{{\xi }_1{\xi }_2}& =\frac{1}{{\sigma }_{{\xi }_1}{\sigma }_{{\xi }_2}}{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }(x-{\bar{\xi }}_1)(y-{\bar{\xi }}_2{)}^{\ast }{p}_{{\xi }_1}(x)p_{{\xi }_2}(y)dxdy\\ & =\frac{1}{{\sigma }_{{\xi }_1}{\sigma }_{{\xi }_2}}{\int }_{-\infty }^{\infty }(x-{\bar{\xi }}_1)p_{{\xi }_1}(x)dx{\int }_{-\infty }^{\infty }(y-{\bar{\xi }}_2{)}^{\ast }{p}_{{\xi }_2}(y)dy\\ & =0\end{array}\text{\hspace{1em}()}$$

示例4：随机变量的线性组合

考虑随机变量的线性组合：
$$\xi =\sum _{n=1}^N{c}_n{\xi }_n\text{\hspace{1em}(8.27)}$$

其中${\xi }_n$是随机变量，$c_n$是确定性常数。无论是否相关，$\xi$的均值为：
E{ξ}=∑n=1NcnE{ξn}(8.28)E\{\xi\} = \sum_{n=1}^{N} c_n E\{\xi_n\} \tag{8.28} E{ξ}=n=1∑N​cn​E{ξn​}(8.28)

对于方差，仅当${\xi }_n$相互不相关或独立时，下式才成立：
$${\sigma }_{\xi }^2=\sum _{n=1}^N{c}_n^2{\sigma }_{{\xi }_n}^2\text{\hspace{1em}(8.29)}$$

以两个实随机变量为例：
$$\begin{array}{rl}\text{var}\left\{\sum _{n=1}^2{c}_n{\xi }_n\right\}& =E\{[(c_1{\xi }_1+c_2{\xi }_2)-(c_1{\bar{\xi }}_1+c_2{\bar{\xi }}_2){]}^2\}\\ & =E\{[c_1({\xi }_1-{\bar{\xi }}_1)+c_2({\xi }_2-{\bar{\xi }}_2){]}^2\}\\ & =c_1^{2}E\{({\xi }_1-{\bar{\xi }}_1{)}^2\}+2c_1{c}_{2}E\{({\xi }_1-{\bar{\xi }}_1)({\xi }_2-{\bar{\xi }}_2)\}\\ & +c_2^{2}E\{({\xi }_2-{\bar{\xi }}_2{)}^2\}\end{array}\text{\hspace{1em}(8.30)}$$

方程(8.30)中的第一项和最后一项分别是$c_1^2{\sigma }_{{\xi }_1}^2$和$c_2^2{\sigma }_{{\xi }_2}^2$。如果${\xi }_1$和${\xi }_2$不相关，则中间项为零。

示例5：信噪比改善

利用关系(8.29)，可以推导信号平均的信噪比改善规律：$N$次信号平均使信噪比提高$\sqrt{N}$倍。

设$\hat{x}=x+\xi$为测量量，包含真实信号$x$和噪声分量$\xi$（零均值，标准差${\sigma }_{\xi }$）。单次测量的信噪比为：
$$(S/N{)}_{\hat{x}}=|x|/{\sigma }_{\xi }$$

进行$N$次测量，得：
$$\hat{y}=\frac{1}{N}\sum _{n=1}^N{\hat{x}}_n=x+\frac{1}{N}\sum _{n=1}^N{\xi }_n$$

假设不同时刻的测得的噪声之间是不相关。，则$\hat{y}$的信噪比为：
$$(S/N{)}_{\hat{y}}=\frac{|x|}{\sqrt{\text{var}\left\{\frac{1}{N}{\sum }_{n=1}^N{\hat{x}}_n\right\}}}=\sqrt{N}\frac{|x|}{{\sigma }_{\xi }}=\sqrt{N}(S/N{)}_{\hat{x}}\text{\hspace{1em}(8.31)}$$

可以看到，平均后的信噪比提高了$\sqrt{N}$倍，不是$N$倍。

随机信号

在成像实验中采集到的随机信号，需用具有随机取值的函数来描述，这类函数被称为随机过程。

• 记随机过程为 $\xi (t)$，则其在任一特定时刻 $t_0$ 的取值 $\xi (t_0)$ 是一个随机变量。
• 该过程的每一个具体的样本函数 ${\xi }_m(t)$ 却是时间的一个确定性函数。
• 随机过程 $\xi (t)$ 亦可被视为一族样本函数的集合，即 ξ(t)={ξm(t)}\xi(t) = \{\xi_m(t)\}ξ(t)={ξm​(t)}。

实际测量中单次获取的噪声信号，即对应于产生该信号的底层随机过程（或噪声源）的一个样本函数 ${\xi }_m(t)$。理想情况下，若能在“完全相同的条件”下进行多次独立的同步测量，所获得的所有样本函数构成的集合，便完整地定义了这个随机过程。

注：此处的“完全相同的条件”是一个理论假设，旨在确保所有样本函数源于同一统计规律。

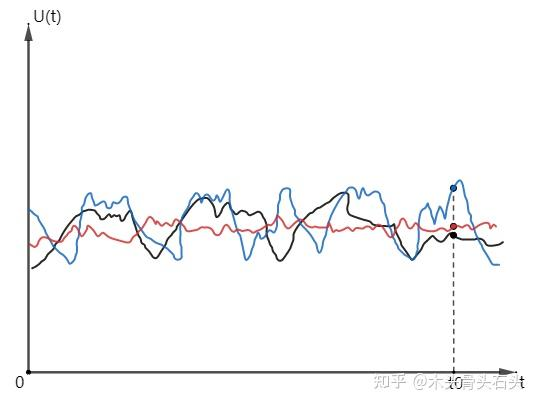
可以用下面的这个例子（引用随机过程：一、随机过程的分布及其特征 - 知乎）来更加通俗的理解随机过程的概念。比如，我们收集 $t$ 时间段内，电子元件的热噪声电压。每次随机试验都可以得到一个$U(t)$的函数，而且每次试验的函数曲线都不一样。我们把试验结果画到同一个坐标系中，可以看到在$t_0$时刻， $U(t_0)$ 的结果有无数个且服从某一分布，因此我们把这种不确定现象称为随机过程，其中：

• 每一个 $t_0$ 时刻的取值 $U(t_0)$ 是一个随机变量，如下图的红、黑、蓝三点
• $0\le t_0\le t$ 的所有取值$U(t)$就是随机过程的一个样本函数或样本曲线，如下面的红、黑、蓝三线。
  

与处理随机变量时类似，我们通常并不需要（或者实际上无法获得）一个随机过程的完整统计描述。在这种情况下，我们（无论是出于选择还是不得已）会转而使用其各种统计矩来进行分析。其中最重要的几个统计矩将在下文讨论。

均值：
ξˉ(t)=E{ξ(t)}(8.32)\bar{\xi}(t) = E\{\xi(t)\} \tag{8.32} ξˉ​(t)=E{ξ(t)}(8.32)

方差：
$${\sigma }_{\xi }^2(t)=E\{[\xi (t)-\bar{\xi }(t)][\xi (t)-\bar{\xi }(t){]}^{\ast }\}\text{\hspace{1em}(8.33)}$$

和相关函数：
R(t,t+τ)=E{ξ(t)ξ∗(t+τ)}(8.34)R(t, t+\tau) = E\{\xi(t) \xi^{*}(t+\tau)\} \tag{8.34} R(t,t+τ)=E{ξ(t)ξ∗(t+τ)}(8.34)

对于某些随机过程，均值和方差与时间无关，相关函数仅依赖于时间差$\tau$，即$R(t,t+\tau )=R(\tau )$。这些过程称为宽平稳过程。

随机过程的另一个重要属性是各态历经性，即时间平均和集合平均可互换，相当于用时间换空间：

• 空间：多个实验在某一个时刻同时做：1万个人同时扔硬币
• 时间：同个实验在一段时间内重复的做：一个人扔一个硬币1万次

对于各态历经过程$\xi (t)$，有：
ξˉ=E{ξ(t)}=⟨ξ(t)⟩(8.35)\bar{\xi} = E\{\xi(t)\} = \langle \xi(t) \rangle \tag{8.35} ξˉ​=E{ξ(t)}=⟨ξ(t)⟩(8.35)

$${\sigma }_{\xi }^2=E\{[\xi (t)-\bar{\xi }][\xi (t)-\bar{\xi }{]}^{\ast }\}=⟨[\xi (t)-\bar{\xi }][\xi (t)-\bar{\xi }{]}^{\ast }⟩\text{\hspace{1em}(8.36)}$$

R(τ)=E{ξ(t)ξ∗(t+τ)}=⟨ξ(t)ξ∗(t+τ)⟩(8.37)R(\tau) = E\{\xi(t) \xi^{*}(t+\tau)\} = \langle \xi(t) \xi^{*}(t+\tau) \rangle \tag{8.37} R(τ)=E{ξ(t)ξ∗(t+τ)}=⟨ξ(t)ξ∗(t+τ)⟩(8.37)

其中$⟨\cdot ⟩$是时间平均算子，定义为：
$$⟨x(t)⟩=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-T}^{T}x(t)dt\text{\hspace{1em}(8.38)}$$

下面这张图很好的展示了时间平均和集平均的区别和联系（图片来自于知乎：时间平均（time average）与集平均（ensemble average） - 知乎）

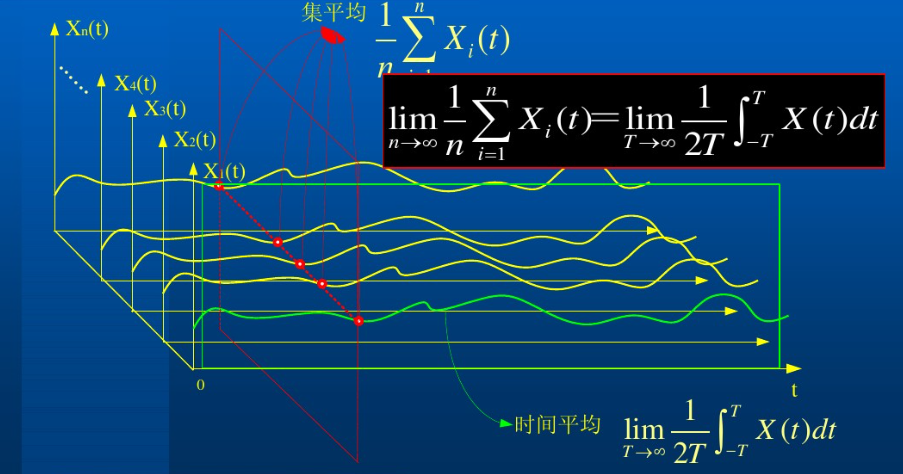
上图红线，它表示有 $N$（$i=1,2,3,......,N,N\to \infty$）个地方都在同时(在t时刻)进行着相同的试验，每个试验的结果为$X_i(t)$，那么$t$时刻的集平均（也就是数学期望）：
ξˉ=E{X(t)}=1N∑i=1NXi(t)N→∞()\bar{\xi}=E\{X(t)\} = \frac{1}{N} \sum_{i=1}^{N} {X}_i(t) \quad N \to \infty \tag{} ξˉ​=E{X(t)}=N1​i=1∑N​Xi​(t)N→∞()
上图绿线，他表示同一个试验(第$i$个)被执行了无数回，我们可以得到这么多试验的平均结果：
$$\bar{\xi }=⟨X_i(t)⟩=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-T}^T{X}_i(t)dt\text{\hspace{1em}()}$$

因此，对于各态历经过程，统计矩可以从任何样本函数中测量。后文中处理的噪声信号假定属于此类。此外，对于各态历经过程，$R(\tau )$是时间的确定性函数，其傅里叶变换给出功率谱密度函数——这一关系由著名的维纳定理建立。如果谱密度函数在测量频率范围内是常数，则该噪声在实践中称为白噪声。

数据域中的噪声特性

随机噪声是磁共振成像中的重要限制因素。它在信号生成和检测阶段就被引入，然后在图像重建阶段进行处理。为便于分析，我们使用${\xi }_d$表示数据域中的噪声分量，${\xi }_I$表示图像域中的噪声分量。实际应用中，${\xi }_d$取决于多个因素，特别是射频检测系统的实际配置。本节假设${\xi }_d$是来自各态历经、平稳、不相关、白噪声过程的加性噪声，具有零均值和标准差${\sigma }_d$。基于此假设，我们得到以下统计特性：
$$\{\begin{array}{l}⟨{\xi }_d(k)⟩=0\\ ⟨{\xi }_d(k){\xi }_d^{\ast }(k)⟩={\sigma }_d^2\\ ⟨{\xi }_d(k){\xi }_d^{\ast }(k+k_0)⟩=0,k_0\ne 0\end{array}\text{\hspace{1em}(8.39)}$$

噪声污染的$k$空间信号（接收线圈上接收到的信号在解调后的数据就是$k$空间数据，我们假设所有的随机噪声都折算到$k$空间数据上）表示为：
$$\hat{S}(k)=S(k)+{\xi }_d(k)\text{\hspace{1em}(8.40)}$$

图像重建后得到：
$$\hat{I}(x)=I(x)+{\xi }_I(x)\text{\hspace{1em}(8.41)}$$

显然，${\xi }_I(x)$的特性取决于所使用的图像重建方案。下面将分析不同重建方法中的噪声传播特性（或者我们可以称之为噪声传递函数）。

直接FFT重建中的噪声

假设采集$N$个噪声$k$空间数据点并使用标准FFT重建算法处理。图像噪声由下式给出：
$${\xi }_I[m]=\frac{1}{N}\sum _{n=-N/2}^{N/2-1}{\xi }_d[n]e^{i2\pi mn/N},-N/2\le m<N/2\text{\hspace{1em}(8.42)}$$

该图像噪声的特点可以从式(8.42)中推导出来：

(a) 零均值特性
图像噪声${\xi }_I[m]$的均值为零：

E{ξI[m]}=0(8.43)E\{\xi_I[m]\} = 0 \tag{8.43} E{ξI​[m]}=0(8.43)

利用式(8.42) 、(8.28)、(8.39)可推导得到(8.43)：
E{ξI[m]}=E{1N∑n=−N/2N/2−1ξd[n]ei2πmn/N}=1N∑n=−N/2N/2−1ei2πmn/NE{ξd[n]}=1N∑n=−N/2N/2−1ei2πmn/N⋅0=0()\begin{aligned} E\{\xi_I[m]\} &= E\{\frac{1}{N} \sum_{n=-N/2}^{N/2-1} \xi_d[n] e^{i2\pi mn/N}\}\\ &=\frac{1}{N} \sum_{n=-N/2}^{N/2-1} e^{i2\pi mn/N} E\{ \xi_d[n]\}\\ &=\frac{1}{N} \sum_{n=-N/2}^{N/2-1} e^{i2\pi mn/N} \cdot 0\\ &=0 \end{aligned} \tag{} E{ξI​[m]}​=E{N1​n=−N/2∑N/2−1​ξd​[n]ei2πmn/N}=N1​n=−N/2∑N/2−1​ei2πmn/NE{ξd​[n]}=N1​n=−N/2∑N/2−1​ei2πmn/N⋅0=0​()

(b) 方差计算
图像噪声的方差为：
$${\sigma }_I^2=\frac{1}{N}{\sigma }_d^2\text{\hspace{1em}(8.44)}$$

或者是
$${\sigma }_I=\sqrt{\frac{1}{N}}{\sigma }_d\text{\hspace{1em}()}$$

利用式(8.42) 、(8.29)、(8.39)可推导得到(8.44)：
$$
\begin{aligned}
\sigma_I^2 &= E{(\xi_I[m] - \bar{\xi_I[m]})(\xi_I[m] - \bar{\xi_I[m]})^{}}\
&= E{(\xi_I[m] - 0)(\xi_I[m] - 0)^{}}\
&= E{ \frac{1}{N} \sum_{p=-N/2}^{N/2-1} \xi_d[p] e^{i2\pi mp/N} \cdot \frac{1}{N} \sum_{q=-N/2}^{N/2-1} \xi_d[q]^* e^{-i2\pi mq/N} }\
&= E\left { \frac{1}{N^2} \sum_{p=-N/2}^{{N/2-1}\sum_{q=-N/2}}{N/2-1} \left [ \xi_d[p] \xi_d[q]^* \cdot e^{i2\pi mp/N} e^{-i2\pi mq/N} \right] \right}\
&= E\left { \frac{1}{N^2} \sum_{p=-N/2}^{{N/2-1}\sum_{q=-N/2}}{N/2-1} \left [ \xi_d[p] \xi_d[q]^* \cdot e^{i2\pi m(p-q)/N} \right] \right}\
&= E\left { \xi_d[p] \xi_d[q]^* \right} \frac{1}{N^2} \sum_{p=-N/2}^{{N/2-1}\sum_{q=-N/2}}{N/2-1} e^{i2\pi m(p-q)/N} \
\
&利用线性无关,当且仅当p=q时，才不为0，可得\
&= E\left { \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} \left [ \xi_d[p] \xi_d[p]^* \ \right] \right} \
&= E{ \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} \xi_d[p]^2 }\

&= \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} E{\xi_d[p]^2 }\
&= \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} \sigma_d^2 \
&= \frac{1}{N^2} \cdot N \cdot \sigma_d^2 \
& = \frac{1}{N} \sigma_d^2
\end{aligned} \tag{}
$$

© 像素间不相关性
图像噪声在不同像素间不相关：
E{ξI[m]ξI∗[n]}=0,对于 m≠n(8.45)E\{\xi_I[m] \xi_I^*[n]\} = 0, \quad \text{对于} \ m \neq n \tag{8.45} E{ξI​[m]ξI∗​[n]}=0,对于 m=n(8.45)

根据定义展开计算：
E{ξI[m]ξI∗[n]}=1N2∑p=−N/2N/2−1∑q=−N/2N/2−1E{ξd[p]ξd∗[q]}ei2π(mp−nq)/N=1N2∑p=−N/2N/2−1E{ξd[p]ξd∗[p]}ei2π(m−n)p/N=1N2σd2∑p=−N/2N/2−1ei2π(m−n)p/N={1Nσd2m=n0其他情况\begin{aligned} E\{\xi_I[m] \xi_I^*[n]\} &= \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} \sum_{q=-N/2}^{N/2-1} E\{\xi_d[p] \xi_d^*[q]\} e^{i2\pi (mp - nq)/N} \\ &= \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} E\{\xi_d[p] \xi_d^*[p]\} e^{i2\pi (m-n)p/N} \\ &= \frac{1}{N^2} \sigma_d^2 \sum_{p=-N/2}^{N/2-1} e^{i2\pi (m-n)p/N} \\ &= \begin{cases} \frac{1}{N} \sigma_d^2 & m = n \\ 0 & \text{其他情况} \end{cases} \end{aligned} E{ξI​[m]ξI∗​[n]}​=N21​p=−N/2∑N/2−1​q=−N/2∑N/2−1​E{ξd​[p]ξd∗​[q]}ei2π(mp−nq)/N=N21​p=−N/2∑N/2−1​E{ξd​[p]ξd∗​[p]}ei2π(m−n)p/N=N21​σd2​p=−N/2∑N/2−1​ei2π(m−n)p/N={N1​σd2​0​m=n其他情况​​

信噪比分析

备注1 方程(8.44)表明，就噪声方差而言，FFT处理等效于进行$N$点信号平均。

备注2 FFT（等效是N点平均）后，图像每像素的信噪比与$\sqrt{N}$成反比：
$$\text{SNR}{|}_{\text{pixel}}\propto \frac{1}{\sqrt{N}}\text{\hspace{1em}(8.46)}$$

通过计算平均信号强度可得更精确表达式：
$$\begin{array}{rl}{I}_{\text{avg}}^2& =\frac{1}{N}\sum _{m=-N/2}^{N/2-1}I[m]I^{\ast }[m]\\ & =\frac{1}{N^3}\sum _{m=-N/2}^{N/2-1}\sum _{p=-N/2}^{N/2-1}\sum _{q=-N/2}^{N/2-1}S[p]S^{\ast }[q]e^{i2\pi (p-q)m/N}\\ & =\frac{1}{N^2}\sum _{n=-N/2}^{N/2-1}|S[n]{|}^2\end{array}\text{\hspace{1em}(8.47)}$$

或者
$$\begin{array}{r}{I}_{\text{avg}}=\frac{1}{N}\sqrt{\sum _{n=-N/2}^{N/2-1}|S[n]{|}^2}\end{array}\text{\hspace{1em}()}$$
因此每像素平均信噪比为：
$$\begin{array}{rl}\text{SNR}{|}_{\text{pixel}}=\frac{I_{\text{avg}}}{{\sigma }_I}& =\frac{\frac{1}{N}\sqrt{{\sum }_{n=-N/2}^{N/2-1}|S[n]{|}^2}}{\sqrt{\frac{1}{N}}{\sigma }_d}\\ & =\frac{\sqrt{{\sum }_{n=-N/2}^{N/2-1}|S[n]{|}^2}}{\sqrt{N}{\sigma }_d}\end{array}\text{\hspace{1em}(8.48)}$$

备注3 设${\hat{I}}_1[m]$为噪声污染的FFT图像，定义：
$${\hat{I}}_2[m]=\frac{1}{P}\sum _{p=0}^{P-1}{\hat{I}}_1(m+p)\text{\hspace{1em}(8.49)}$$

则${\hat{I}}_2[m]$的信噪比比${\hat{I}}_1[m]$提高$\sqrt{P}$倍。上述操作其实就是平均。

零填充FFT重建中的噪声

使用零填充FFT重建算法时，$N$个噪声数据点产生$M$（$M>N$）个噪声图像点：
$${\xi }_I[m]=\frac{1}{N}\sum _{n=-N/2}^{N/2-1}{\xi }_d[n]e^{i2\pi mn/M},-M/2\le m<M/2\text{\hspace{1em}(8.50)}$$

噪声特性

(a) 零均值特性
E{ξI[m]}=0(8.51)E\{\xi_I[m]\} = 0 \tag{8.51} E{ξI​[m]}=0(8.51)

(b) 方差计算
$${\sigma }_I^2=\frac{1}{N}{\sigma }_d^2\text{\hspace{1em}(8.52)}$$

© 像素间相关性
E{ξI[m]ξI∗[n]}=1N2σd2sin⁡[π(m−n)N/M]sin⁡[π(m−n)/M]e−iπ(m−n)/N(8.53)E\{\xi_I[m] \xi_I^*[n]\} = \frac{1}{N^2} \sigma_d^2 \frac{\sin[\pi (m-n)N/M]}{\sin[\pi (m-n)/M]} e^{-i\pi (m-n)/N} \tag{8.53} E{ξI​[m]ξI∗​[n]}=N21​σd2​sin[π(m−n)/M]sin[π(m−n)N/M]​e−iπ(m−n)/N(8.53)

比较方程(8.51)-(8.52)与(8.43)-(8.44)可知，零填充不影响图像噪声的均值和方差，因此图像信噪比保持不变。然而，零填充改变了图像噪声的统计独立性，如方程(8.53)所示。由于这一特性，备注3中的结论在此不适用。换句话说，P个点的近邻像素平均将不能获得$\sqrt{P}$ 的信噪比提升。

式(8.53)的详细推导过程：
E{ξI[m]ξI∗[n]}=1N2∑p=−N/2N/2−1∑q=−N/2N/2−1E{ξd[p]ξd∗[q]}ei2π(mp−nq)/M=1N2∑p=−N/2N/2−1E{ξd[p]ξd∗[p]}ei2π(m−n)p/M=1N2σd2∑p=−N/2N/2−1ei2π(m−n)p/M=1N2σd2sin⁡[π(m−n)N/M]sin⁡[π(m−n)/M]e−iπ(m−n)/N\begin{aligned} E\{\xi_I[m] \xi_I^*[n]\} &= \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} \sum_{q=-N/2}^{N/2-1} E\{\xi_d[p] \xi_d^*[q]\} e^{i2\pi (mp - nq)/M} \\ &= \frac{1}{N^2} \sum_{p=-N/2}^{N/2-1} E\{\xi_d[p] \xi_d^*[p]\} e^{i2\pi (m-n)p/M} \\ &= \frac{1}{N^2} \sigma_d^2 \sum_{p=-N/2}^{N/2-1} e^{i2\pi (m-n)p/M} \\ &= \frac{1}{N^2} \sigma_d^2 \frac{\sin[\pi (m-n)N/M]}{\sin[\pi (m-n)/M]} e^{-i\pi (m-n)/N} \end{aligned} E{ξI​[m]ξI∗​[n]}​=N21​p=−N/2∑N/2−1​q=−N/2∑N/2−1​E{ξd​[p]ξd∗​[q]}ei2π(mp−nq)/M=N21​p=−N/2∑N/2−1​E{ξd​[p]ξd∗​[p]}ei2π(m−n)p/M=N21​σd2​p=−N/2∑N/2−1​ei2π(m−n)p/M=N21​σd2​sin[π(m−n)/M]sin[π(m−n)N/M]​e−iπ(m−n)/N​

小结

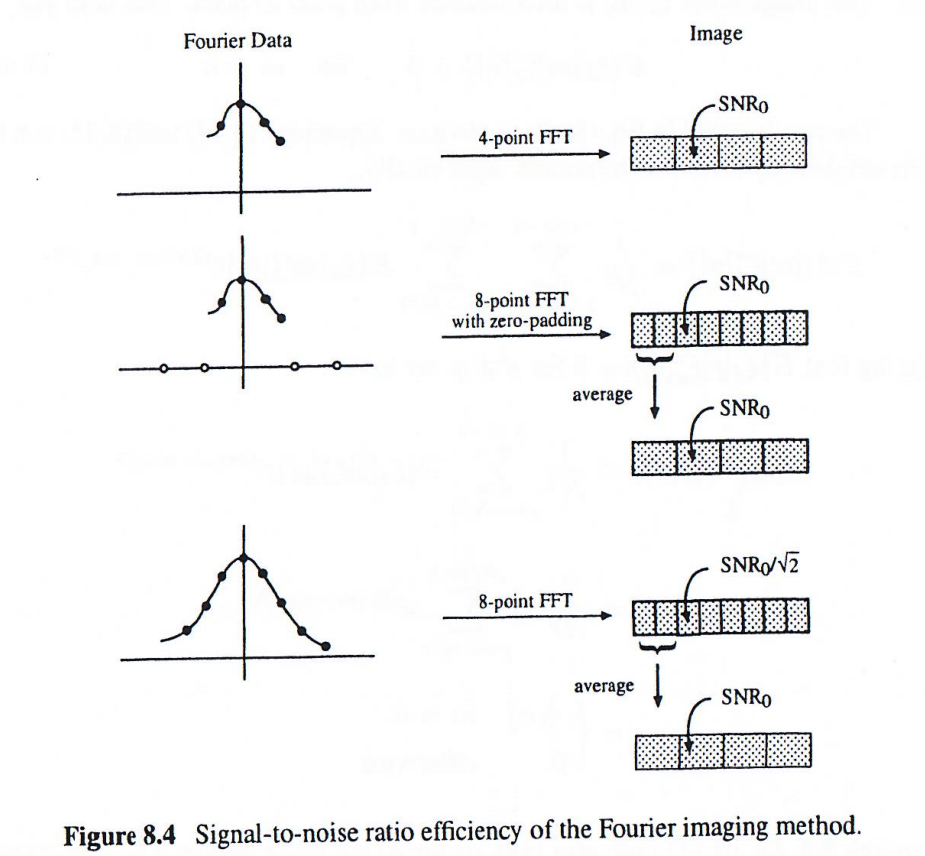
为了深入理解直接FFT重建和零填充FFT重建在磁共振成像中的噪声特性差异，我们设计了一个理论验证实验。如下图所示，考虑一个一维成像对象和四个傅里叶空间采样点的情况。

• 当采用标准FFT算法对四个k空间采样点进行直接重建时，将获得由四个像素组成的图像，其信噪比定义为SNR₀。这种重建方式保持了采样数据的原始分辨率。

• 若将原始四个采样点通过零填充扩展到八个点后进行FFT重建，将得到八个像素的图像。重要的是，这些像素的信噪比仍然保持为SNR₀。需要特别说明的是，在这两种重建方法中，傅里叶像素尺寸保持不变，每个像素承载的信号强度也保持一致。

• 当尝试将零填充产生的八个像素重新合并为四个像素时，由于噪声分量之间存在相关性，这种操作不会带来信噪比的提升。这一现象揭示了零填充处理虽然增加了表观分辨率，但并未引入新的独立信息。

• 如果通过实际采集获得八个相位编码测量值（旨在提高空间分辨率），则新重建图像的信噪比SNR₁将近似为SNR₀/√2。需要说明的是，由于新增采样点会贡献额外的信号能量，实际信噪比下降幅度会略小于理论值具体数值，可通过式(8.48)进行精确计算。

• 将八个像素合并为四个像素后，虽然可以恢复原始信噪比水平，但成像时间需要增加一倍。这种操作导致信噪比效率（SNR效率）降低为原来的√2分之一。这一结果凸显了采样扩展带来的效率损失。

通过傅里叶重建方法提升空间分辨率时，扩展$k$空间采样会导致信噪比效率出现不可逆的损失。这一发现对于磁共振成像序列优化和采样策略选择具有重要指导意义。

滤波反投影重建中的噪声

（后续再丰富一下内容）

考虑使用"M"滤波器的二维滤波反投影重建。设${\xi }_d[m,n]={\xi }_d(m\Delta k,n\Delta \varphi )$为极坐标$k$空间数据集中的加性噪声，包含$N_{\varphi }$条径向线，每条$N_p$个点。图像噪声为：
$${\xi }_I(x,y)=\frac{\pi }{N_{\varphi }}\frac{1}{N_p}\sum _{n=-N_{\varphi }/2}^{N_{\varphi }/2-1}\sum _{m=0}^{N_p-1}\frac{|m|}{N_p}{\xi }_d[m,n]e^{i2\pi mp}\text{\hspace{1em}(8.54)}$$

其中$p=x\cos (m\pi /N_{\varphi })+y\sin (m\pi /N_{\varphi })$，$\Delta k=1/N_p$。

(a) 零均值条件
如果数据噪声均值为零，则图像噪声也具有零均值：
E{ξI(x,y)}=0若E{ξd[m,n]}=0(8.55)E\{\xi_I(x,y)\} = 0 \quad \text{若} \quad E\{\xi_d[m,n]\} = 0 \tag{8.55} E{ξI​(x,y)}=0若E{ξd​[m,n]}=0(8.55)

(b) 方差推导
假设${\xi }_d[m,n]$在不同测量间不相关，图像噪声方差为：
var{ξI(x,y)}=(πNϕNp)2∑n=−Nϕ/2Nϕ/2−1∑m=0Np−1(mNp)2var{ξd[m,n]}(8.56)\text{var}\{\xi_I(x,y)\} = \left( \frac{\pi}{N_\phi N_p} \right)^2 \sum_{n=-N_\phi/2}^{N_\phi/2-1} \sum_{m=0}^{N_p-1} \left( \frac{m}{N_p} \right)^2 \text{var}\{\xi_d[m,n]\} \tag{8.56} var{ξI​(x,y)}=(Nϕ​Np​π​)2n=−Nϕ​/2∑Nϕ​/2−1​m=0∑Np​−1​(Np​m​)2var{ξd​[m,n]}(8.56)

使用var{ξI(x,y)}=σI2\text{var}\{\xi_I(x,y)\} = \sigma_I^2var{ξI​(x,y)}=σI2​和var{ξd[m,n]}=σd2\text{var}\{\xi_d[m,n]\} = \sigma_d^2var{ξd​[m,n]}=σd2​，可得：
$$\begin{array}{rl}{\sigma }_I^2& ={\left(\frac{\pi }{N_{\varphi }{N}_p}\right)}^2\sum _{m=0}^{N_p-1}\sum _{n=-N_{\varphi }/2}^{N_{\varphi }/2-1}{\left(\frac{m}{N_p}\right)}^2{\sigma }_d^2\\ & \approx \frac{{\pi }^2}{12}\frac{1}{N_p{N}_{\varphi }}{\sigma }_d^2\end{array}\text{\hspace{1em}(8.57)}$$
其中使用了${\sum }_{m=0}^N{m}^2=\frac{1}{6}N(N+1)(2N+1)\approx \frac{1}{3}{N}^3$。

与傅里叶成像对比

对于具有$N_x\times N_y$笛卡尔点的二维傅里叶成像：
σI2=1Nx2Ny2∑n=−Nx/2−1Nx/2∑m=−Ny/2Ny/2−1var{ξd[m,n]}=1NxNyσd2(8.58)\begin{aligned} \sigma_I^2 &= \frac{1}{N_x^2 N_y^2} \sum_{n=-N_x/2-1}^{N_x/2} \sum_{m=-N_y/2}^{N_y/2-1} \text{var}\{\xi_d[m,n]\} \\ &= \frac{1}{N_x N_y} \sigma_d^2 \end{aligned} \tag{8.58} σI2​​=Nx2​Ny2​1​n=−Nx​/2−1∑Nx​/2​m=−Ny​/2∑Ny​/2−1​var{ξd​[m,n]}=Nx​Ny​1​σd2​​(8.58)
其中${\xi }_d[m,n]$表示${\xi }_d(m\Delta k_x,n\Delta k_y)$。

因此，当$N_x{N}_y=N_p{N}_{\varphi }$时：
$$\frac{{\sigma }_I(\text{FBP})}{{\sigma }_I(\text{FT})}\approx \frac{\pi }{\sqrt{12}}<1\text{\hspace{1em}(8.59)}$$

FFT重建的图像噪声略低于滤波反投影重建