当前位置：首页 > news >正文

LeetCode 2536.子矩阵元素加 1：二维差分数组

news 2025/11/15 13:16:53

【LetMeFly】2536.子矩阵元素加 1：二维差分数组

力扣题目链接：https://leetcode.cn/problems/increment-submatrices-by-one/

给你一个正整数 n ，表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ，矩阵中填满了 0 。

另给你一个二维整数数组 query 。针对每个查询 query[i] = [row1_i, col1_i, row2_i, col2_i] ，请你执行下述操作：

找出 左上角 为 (row1_i, col1_i) 且 右下角 为 (row2_i, col2_i) 的子矩阵，将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1_i <= x <= row2_i 和 col1_i <= y <= col2_i 的 mat[x][y] 加 1 。

返回执行完所有操作后得到的矩阵 mat 。

示例 1：

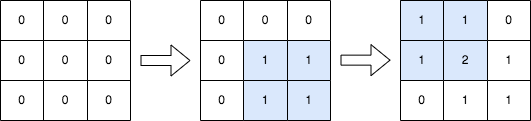
输入：n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出：[[1,1,0],[1,2,1],[0,1,1]]
解释：上图所展示的分别是：初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作：将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。 
- 第二个操作：将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。

示例 2：

输入：n = 2, queries = [[0,0,1,1]]
输出：[[1,1],[1,1]]
解释：上图所展示的分别是：初始矩阵、执行完第一个操作后的矩阵。 
- 第一个操作：将矩阵中的每个元素加 1 。

提示：

1 <= n <= 500
1 <= queries.length <= 10⁴
0 <= row1_i <= row2_i < n
0 <= col1_i <= col2_i < n

Long time no see.

解题方法：二维差分数组

使用二维差分数组diff，其中令diff[i][j]表示原数组mat[i][j]到mat[n-1][n-1]每个元素变化值。

例如将mat[x1][y1]到mat[x2][y2]每个元素值加一，反映到差分数组上就表现为：

$d i ff [x 1] [y 1] + = 1$ ，先从mat[x1][y1]到mat[n-1][n-1]每个元素都加一
$d i ff [x 2 + 1] [y 1] - = 1$ ，由于从mat[x2+1][y1]到mat[n-1][n-1]每个元素无需改变，第一步加的范围太大了，不该变的撤销变化
$d i ff [x 1] [y 2 + 1] - = 1$ ，与2同理，由于从mat[x1][y2+1]到mat[n-1][n-1]每个元素无需改变，第一步加的范围太大了，不该变的撤销变化
$d i ff [x 2 + 1] [y 2 + 1] + = 1$ ，由于第二步和第三步都包含范围mat[x2+1][y2+1]，所以这块“重复撤销”了，再加回来

对于每个query，以 $O (1)$ 的时间复杂度可以计算出diff数组的变化。最终处理完所有query，再由diff差分数组反推出原数组mat就好了。

二维数组思考困难的话可以以一位数组为例，一位差分数组的前缀和数组就是原始数组，二维数组也是如此。只需要对diff数组求前缀和，就能得到原始mat数组了。

前缀和prefix[i][j]代表从diff[0][0]到diff[i][j]的所有元素之和。求前缀和的过程可以由左上到右下的顺序求得。

和求差分数组过程类似， $p re f i x [i] [j] = d i ff [i] [j] + p re f i x [i - 1] [j] + p re f i x [i] [j - 1] - p re f i x [i - 1] [j - 1]$ 。

解释为：从diff[0][0]到diff[i][j]的所有元素之和 $=$ 从diff[0][0]到diff[i-1][j]的所有元素之和 $+$ 从diff[0][0]到diff[i][j-]的所有元素之和 $-$ 从diff[0][0]到diff[i-1][j-1]的所有元素之和（算重了）。

时间复杂度 $O(n^2+len(queries))$
空间复杂度 $O(n^2)$

AC代码

C++

/** @LastEditTime: 2025-11-14 18:07:20*/
class Solution {
public:vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {vector<vector<int>> diff(n + 1, vector<int>(n + 1));for (vector<int>& q : queries) {int x1 = q[0], y1 = q[1], x2 = q[2], y2 = q[3];diff[x1][y1]++;diff[x2 + 1][y1]--;diff[x1][y2 + 1]--;diff[x2 + 1][y2 + 1]++;}vector<vector<int>> ans(n, vector<int>(n));for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {ans[i][j] = diff[i][j] + (i == 0 ? 0 : ans[i - 1][j])+ (j == 0 ? 0 : ans[i][j - 1])- ((i == 0 || j == 0) ? 0 : ans[i - 1][j - 1]);}}return ans;}
};

Python

'''
LastEditTime: 2025-11-14 19:16:40
'''
from typing import Listclass Solution:def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:diff = [[0] * (n + 1) for _ in range(n + 1)]for x1, y1, x2, y2 in queries:diff[x1][y1] += 1diff[x2 + 1][y1] -= 1diff[x1][y2 + 1] -= 1diff[x2 + 1][y2 + 1] += 1ans = [[0] * n for _ in range(n)]for i in range(n):for j in range(n):ans[i][j] = diff[i][j] + \(0 if not i else ans[i - 1][j]) + \(0 if not j else ans[i][j - 1]) - \(0 if not i or not j else ans[i - 1][j - 1])return ans

Go

/** @Author: LetMeFly* @Date: 2025-11-14 19:38:51* @LastEditors: LetMeFly.xyz* @LastEditTime: 2025-11-14 19:46:39*/
package mainfunc rangeAddQueries(n int, queries [][]int) [][]int {diff := make([][]int, n + 1)for i := range diff {diff[i] = make([]int, n + 1)}for _, q := range queries {x1, y1, x2, y2 := q[0], q[1], q[2], q[3]diff[x1][y1]++diff[x2 + 1][y1]--diff[x1][y2 + 1]--diff[x2 + 1][y2 + 1]++}ans := make([][]int, n)for i := range ans {ans[i] = make([]int, n)}for i := range ans {for j := range ans[i] {up := 0if i > 0 {up = ans[i - 1][j]}left := 0if j > 0 {left = ans[i][j - 1]}lu := 0if i > 0 && j > 0 {lu = ans[i - 1][j - 1]}ans[i][j] = diff[i][j] + left + up - lu}}return ans
}