自己动手写深度学习框架(反向传播)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】
深度学习的原理,远没有它的名字看起来那么复杂。本质上,我们是希望所有的参数都按照梯度的方向去增加,或者是减小,这样可以保证残差方程的积分数值越来越小。那么怎么计算这些梯度数值呢,这就是一个问题。
1、数值法求导太慢了
前面我们说过,可以通过数值法进行求导的。求导的方法,就是保持其他变量不变,只计算当前变量发生改变之后,对应的参数方程数值是多少。通过得到的残差数值,除以变动的变量,就可以得到对应的梯度。这种方法,虽然道理简单,但是计算量太大。一旦遇到复杂一点的深度网络,几乎就是计算的灾难。只有在不太复杂的情况下,比如线性回归,才适合这种做法。
2、反向传播其实就是嵌套求导
假设有这样三个方程,即
y1 = x**2
y2 = y1 + 1
y3 = y2*4
那么这个时候如果希望y3对x进行求导,应该怎么做呢?其实就是一个嵌套求导的过程,y3首先对y2求导,接着y2对y1求导,最后是y1对x求导,所有的结果相乘就是y3对x的求导结果。所以,最终的求导结果就是4 * 1 * 2*x,结果就是8x。
3、反向传播本身是什么意思
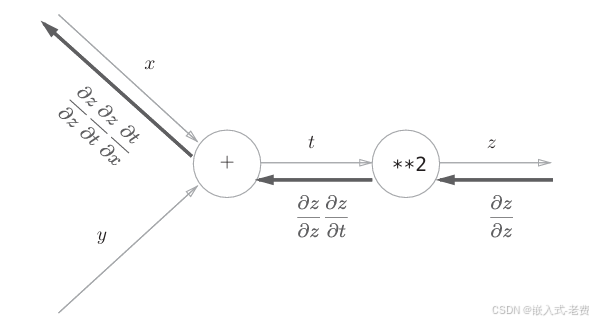
传播是一种夸张的说法,就是顺序计算完之后,接着从后往前一层一层计算导数。就和刚才计算y3对x的求导一样,一层一层往前递进,像声音的传播一样。在这过程当中,可能还涉及到参数的求导,比如假设方程是这样的,
y1 = x**2
y2 = w*y1 + b
y3 = y2*4
这个时候,如果需要实现y3对w的求导,结果是什么样的呢?处理流程是一样的,首先是y3对y2的求导,接着是y2对w的求导,所以结果就是4*y1。因此,y1在前期预测的时候,结果必须要保留下来,这样才能计算y3对w的求导。
4、什么时候更新参数
一般是所有参数的梯度求解之后,统一用梯度下降法去更新参数数值。
5、举例说明如果用反向传播法计算梯度
书中最经典的例子就是计算加法和乘法的梯度。问题的来源是一次购买水果的经历。中间涉及到了加法和乘法。既然如此,如果用梯度向量的概念来理解,最终价格对水果价格的求导,是怎么计算的呢?对水果数量的求导又是怎么计算的呢?
class add:def __init__(self):passdef forward(self, x, y):return x+ydef backward(self, dout):return dout * 1, dout * 1class mul:def __init__(self):self.x = Noneself.y = Nonedef forward(self, x, y):self.x = xself.y = yreturn x*ydef backward(self, dout):return dout* self.y, dout* self.x这里面最有意思的,其实是两个backward的函数。首先假设有一个外界传进来的导数值,比如上面的y3对y2的求导,这个时候其实只要乘上本地的导数,就可以得到想要的结果了。比如,如果本地是对w求导,那么乘上y1即可。 也就是说,如果需要对当前层的参数求导,只需要用输入进来的dout,乘上本层的求导结果即可,这就是反向传播的基本原理。其他层也是同样的处理方法。
