当前位置：首页 > news >正文

深度学习：正则化（Regularization）实践（无正则化 vs 有正则化（L2 正则化、Dropout））

news 2025/11/15 11:36:08

深度学习：什么是正则化（Regularization）？L1 与 L2 正则化的原理与区别

关键词解释：Dropout正则化技术

💡 本教程基于一个经典的二分类任务，演示如何通过 L2 正则化 和 Dropout 来防止神经网络过拟合。

✅ 一、背景知识：什么是正则化？

正则化（Regularization） 是一种防止模型过拟合的技术。其核心思想是：

🔍 在损失函数中加入“惩罚项”，限制模型复杂度，提升泛化能力。

如果想详细了解可以看本文开头的两篇文章

常用方法包括：

L2 正则化（权重衰减）
Dropout
L1 正则化（较少用）

✅ 二、实验设置

2.1 数据集

使用 load_2D_dataset() 加载一个非线性可分的数据集（红点 vs 蓝点），目标是训练一个三层神经网络进行分类。

train_X, train_Y, test_X, test_Y = load_2D_dataset()

2.2 网络结构

构建一个包含 3 层的前馈神经网络：

输入层：2 维特征；
隐藏层 1：20 个神经元；
隐藏层 2：3 个神经元；
输出层：1 个神经元（sigmoid 激活函数）；

layers_dims = [X.shape[0], 20, 3, 1]

2.3 优化器

使用标准梯度下降法（SGD），学习率固定为 0.3。

✅ 三、三种模型对比

模型	是否加正则化	方法
无正则化	❌	基础模型
L2 正则化	✅	添加权重惩罚项
Dropout	✅	训练时随机丢弃神经元

✅ 四、代码实现详解

4.1 主函数：`model()`

支持三种模式：

lambd=0, keep_prob=1 → 无正则化；
lambd>0 → L2 正则化；
keep_prob<1 → Dropout。

def model(X, Y, learning_rate=0.3, num_iterations=30000, print_cost=True, lambd=0, keep_prob=1):# 初始化参数parameters = initialize_parameters(layers_dims)for i in range(num_iterations):if keep_prob == 1:A3, cache = forward_propagation(X, parameters)elif keep_prob < 1:A3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)if lambd == 0:cost = compute_cost(A3, Y)else:cost = compute_cost_with_regularization(A3, Y, parameters, lambd)# 反向传播if lambd == 0 and keep_prob == 1:grads = backward_propagation(X, Y, cache)elif lambd != 0:grads = backward_propagation_with_regularization(X, Y, cache, lambd)elif keep_prob < 1:grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)parameters = update_parameters(parameters, grads, learning_rate)if print_cost and i % 1000 == 0:costs.append(cost)plt.plot(costs)plt.ylabel('cost')plt.xlabel('iterations (x1,000)')plt.title("Learning rate =" + str(learning_rate))plt.show()return parameters

4.2 L2 正则化实现

（1）带正则化的成本函数

def compute_cost_with_regularization(A3, Y, parameters, lambd):m = Y.shape[1]W1, W2, W3 = parameters["W1"], parameters["W2"], parameters["W3"]cross_entropy_cost = compute_cost(A3, Y)  # 原始损失L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)cost = cross_entropy_cost + L2_regularization_costreturn cost

（2）带正则化的反向传播

def backward_propagation_with_regularization(X, Y, cache, lambd):m = X.shape[1](Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = 1./m * np.dot(dZ3, A2.T) + (lambd * W3) / m  # 加上正则项db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)dA2 = np.dot(W3.T, dZ3)dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = 1./m * np.dot(dZ2, A1.T) + (lambd * W2) / mdb2 = 1./m * np.sum(dZ2, axis=1, keepdims=True)dA1 = np.dot(W2.T, dZ2)dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = 1./m * np.dot(dZ1, X.T) + (lambd * W1) / mdb1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,"dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients

✅ 关键点：在 dW 中加上 $( \frac{\lambda}{m} W )$ ，即权重衰减。

4.3 Dropout 实现

（1）前向传播

def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):np.random.seed(1)W1, b1, W2, b2, W3, b3 = parameters.values()Z1 = np.dot(W1, X) + b1A1 = relu(Z1)D1 = np.random.rand(A1.shape[0], A1.shape[1]) < keep_prob  # 生成掩码A1 = A1 * D1  # 关闭部分神经元A1 = A1 / keep_prob  # 缩放剩余值Z2 = np.dot(W2, A1) + b2A2 = relu(Z2)D2 = np.random.rand(A2.shape[0], A2.shape[1]) < keep_probA2 = A2 * D2A2 = A2 / keep_probZ3 = np.dot(W3, A2) + b3A3 = sigmoid(Z3)cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)return A3, cache

⚠️ 注意：仅在训练时使用 Dropout，测试时不使用。

（2）反向传播

def backward_propagation_with_dropout(X, Y, cache, keep_prob):m = X.shape[1](Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = 1./m * np.dot(dZ3, A2.T)db3 = 1./m * np.sum(dZ3, axis=1, keepdims=True)dA2 = np.dot(W3.T, dZ3)dA2 = dA2 * D2  # 乘以掩码dA2 = dA2 / keep_prob  # 缩放dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = 1./m * np.dot(dZ2, A1.T)db2 = 1./m * np.sum(dZ2, axis=1, keepdims=True)dA1 = np.dot(W2.T, dZ2)dA1 = dA1 * D1dA1 = dA1 / keep_probdZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = 1./m * np.dot(dZ1, X.T)db1 = 1./m * np.sum(dZ1, axis=1, keepdims=True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,"dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients

✅ 关键点：反向传播时也要乘以掩码并缩放。

✅ 五、实验结果分析（图像解读）

图1：无正则化模型 → 明显过拟合

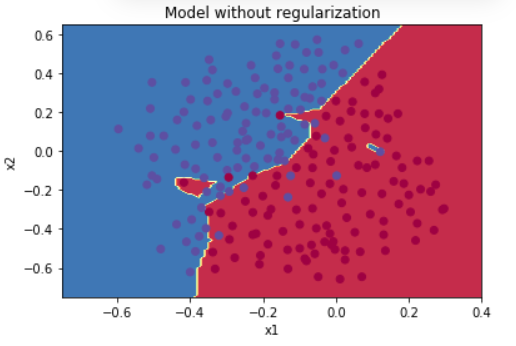
决策边界：非常曲折，试图完美拟合每个点；
问题：对训练数据过度适应，导致泛化能力差；
结论：模型“死记硬背”了训练数据。

图2：L2 正则化模型 → 平滑边界

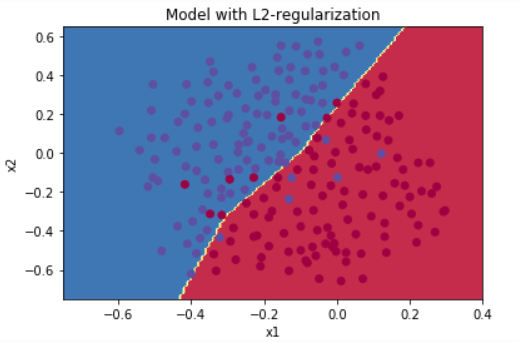
决策边界：更加平滑，不再追求细节；
优点：减少了过拟合，提高了泛化能力；
原理：通过惩罚大权重，使模型更简单。

图3：Dropout 模型 → 类似平滑效果

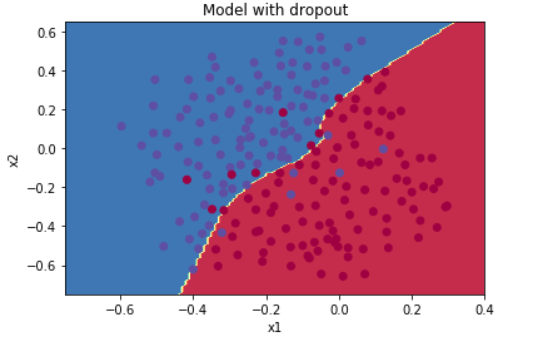
决策边界：同样平滑，但略有不同；
优点：强制神经元独立工作，增强鲁棒性；
原理：训练时随机关闭神经元，防止共依赖。

✅ 六、总结：哪种正则化更好？

方法	是否推荐	原因
无正则化	❌ 不推荐	容易过拟合
L2 正则化	✅ 推荐	简单有效，适合大多数任务
Dropout	✅ 推荐	特别适合深度网络，能防止神经元共依赖