磁共振成像原理（理论）32：分辨率限制 (Resolution Limitations)

本专题主要参考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 8.1

在任何实际的磁共振成像实验中，所得图像永远不会与期望的真实图像完全相同。本节讨论由于有限分辨率引起的图像误差。篇幅有限，我们在这里并不展开去描述限制分辨率的所有因素，而是重点来看看点扩散函数这个概念概念，并展示如何使用它来分析几种实际成像方案中的分辨率限制。

点扩散函数

考虑一个由单点（无限小）组成的理想化物体。我们对该理想物体进行成像，其图像很可能是一个模糊的点（具备一定的分布）。然而，我们仍然能够将其识别为一个点。

现在，我们向物体添加另一个点。如果两个点相距较远，我们将看到两个模糊的点，目前为止，我们还是能够分辨出来，这是两个独立的点。

但是，随着两个点逐渐靠近，图像看起来就不太像两个点了。实际上，当它们的间距低于某个阈值时，这两个点会合并成一个斑点。我们称这个阈值为成像系统的分辨率极限。

正式地说，成像系统的空间分辨率是两个点源在其图像中仍可分辨所需的最小间距$\delta x$。

为了得到更定量的分辨率定义，接下来引入点扩散函数的概念。

我们首先定义什么是线性成像过程。假设对于给定的成像系统，物体$I_1(x)$产生图像${\hat{I}}_1(x)$，物体$I_2(x)$产生图像${\hat{I}}_2(x)$。然后我们构造一个复合物体：
$$I_3(x)=a{I}_1(x)+b{I}_2(x)\text{\hspace{1em}(8.1)}$$

其中$a$和$b$为任意常数。如果$I_3(x)$产生的图像可以由下式描述：
$${\hat{I}}_3(x)=a{\hat{I}}_1(x)+b{\hat{I}}_2(x)\text{\hspace{1em}(8.2)}$$

则该成像系统是一个线性系统。对于这样的系统，在任意物体函数$I(x)$及其图像$\hat{I}(x)$之间存在一个优雅的关系（注意：下面的$\ast$是一个卷积）：
$$\hat{I}(x)=I(x)\ast h(x)\text{\hspace{1em}(8.3)}$$

其中卷积核函数$h(x)$被称为点扩散函数，因为当$I(x)=\delta (x)$时，$\hat{I}(x)=h(x)$，也就是说，对于成像系统而言，即使成像对象是单点的理想物体，也会得到具备一定分布（扩散）的成像图案。

从方程(8.3)可以清楚地看出，只有当点扩散函数$h(x)=\delta (x)$函数时，成像系统的图像才是潜在物体函数的精确表示。此时：
$$\hat{I}(x)=I(x)\ast h(x)=I(x)\ast \delta (x)=I(x)\text{\hspace{1em}(8.3A)}$$

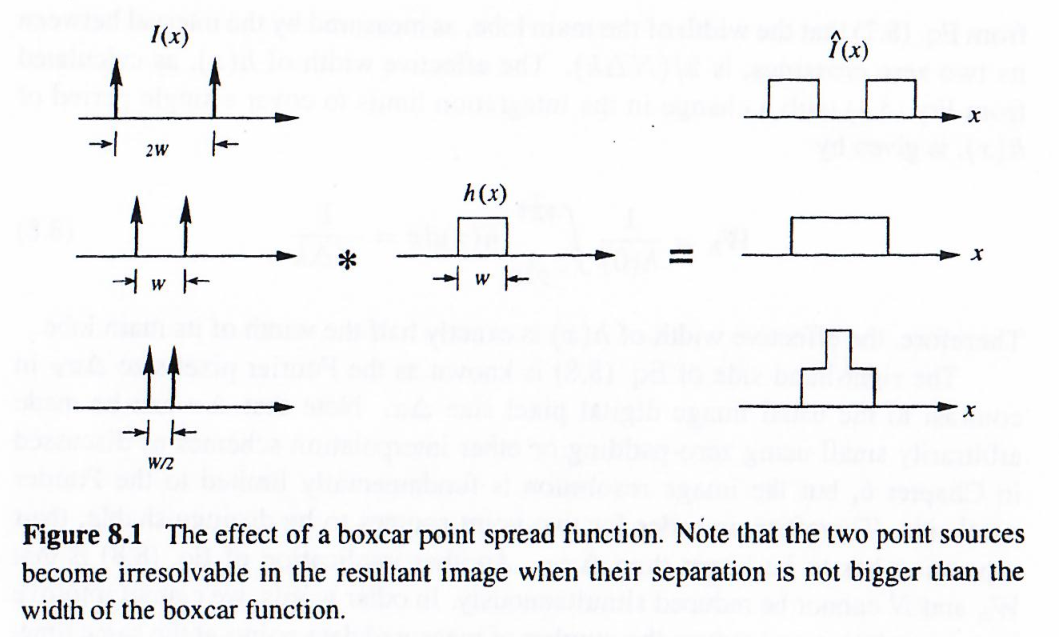
如果$h(x)$偏离$\delta$函数，将是$I(x)$的模糊版本。由不完美的$h(x)$引入到$\hat{I}(x)$的模糊量可以通过的宽度来量化。为了说明这一点，考虑一个简单的情况，假设$h(x)$是一个宽度为$w$的箱形函数。如上图所示，只有当结果图像中的两个源之间的间距大于箱形函数的宽度时，它们才是可分辨的。因此，基于观察，我们可以说：成像系统的分辨率限制是其点扩散函数的宽度。

当$h(x)$不是一个箱形函数时，其宽度的定义并不唯一。以下是两种实用的定义：

定义1：$h(x)$的有效宽度$W_h$是$h(x)$的半高全宽。

定义2：$h(x)$的有效宽度$W_h$是与$h(x)$具有相同高度和面积的近似箱形函数的宽度；或者更准确地说：
$$W_h=\frac{1}{h(0)}{\int }_{-\infty }^{\infty }h(x)dx\text{\hspace{1em}(8.4)}$$

这里假设$h(0)$是$h(x)$的最大值。

傅里叶重建的PSF

为方便起见，我们考虑一维情况。回顾之前的内容式子（6.20），给定$N$个傅里叶样本（有限采样），基于截断的傅里叶级数重建的图像由下式给出：
$$\hat{I}(x)=\Delta k\sum _{n=-N/2}^{N/2-1}S(n\Delta k)e^{i2\pi n\Delta kx}\text{\hspace{1em}(8.5)}$$

为了推导潜在的PSF，我们简单地将真实图像函数$I(x)$设为一个$\delta$函数，然后来查看其傅里叶变换。我们一起回顾一下下图：

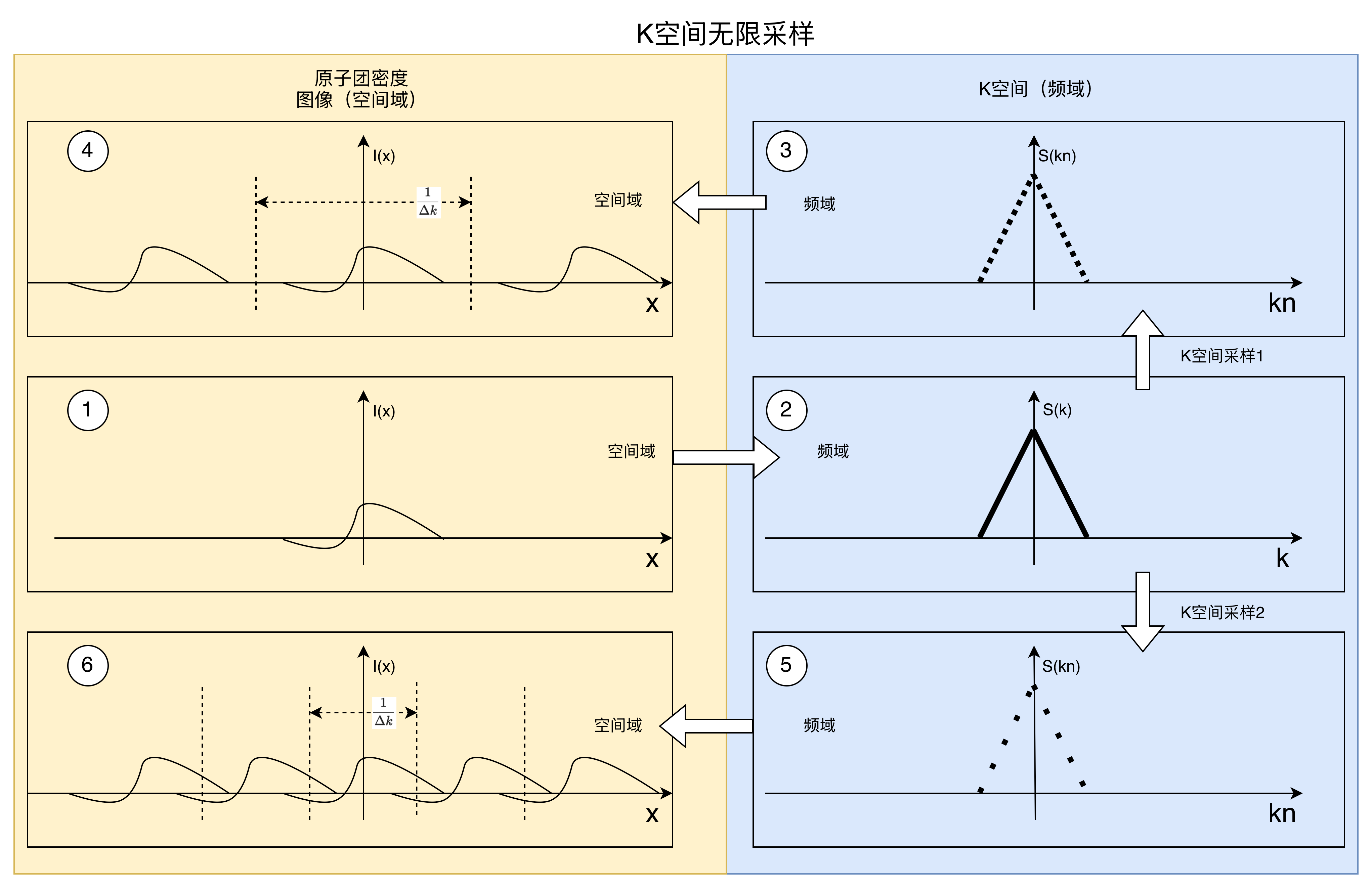
在傅里叶成像中，测量信号$S(k)$（上图2）与物体函数$I(x)$（上图1）通过傅里叶变换相关联：
$$S(k)={\int }_{-\infty }^{\infty }I(x)e^{-i2\pi kx}dx\text{\hspace{1em}(1)}$$

当物体为理想点源时，将$I(x)=\delta (x)$代入方程(1)：
$$S(k)={\int }_{-\infty }^{\infty }\delta (x)e^{-i2\pi kx}dx\text{\hspace{1em}(2)}$$

根据狄拉克$\delta$函数的筛选性质：
$${\int }_{-\infty }^{\infty }\delta (x)f(x)dx=f(0)\text{\hspace{1em}(3)}$$

因此，方程(2)简化为：
$$S(k)=e^{-i2\pi k\cdot 0}=1\text{\hspace{1em}(4)}$$

在离散采样的实际成像中，$k$空间在采样点$k=m\Delta k$处被采样。因此，对于所有采样点（上图2到3）：
$$S(m\Delta k)=1\text{对于所有}m\text{\hspace{1em}(5)}$$

因此，测量信号为$S(m\Delta k)=1$。当我们将看空间采样信号$S(m\Delta k)=1$代入方程(8.5)，并结合式(8.3)，即可得到以下PSF：
$$\hat{I}(x)=I(x)\ast h(x)=\delta (x)\ast h(x)=h(x)=\Delta k\sum _{n=-N/2}^{N/2-1}{e}^{i2\pi n\Delta kx}\text{\hspace{1em}(8.6)}$$

在得到K空间有限采样条件下的点扩散函数之前，让我们假设一下，如果采样点数无限会怎么样？将式（8.6）的求和上下限都改为无穷，即可得到：
$$h_{\infty }(x)=\Delta k\sum _{n=-\infty }^{\infty }{e}^{i2\pi n\Delta kx}\text{\hspace{1em}(1)}$$

由于
$$\sum _{n=-\infty }^{\infty }{e}^{i2\pi nx}=\sum _{m=-\infty }^{\infty }\delta (x-m)\text{\hspace{1em}(2)}$$

令$u=\Delta kx$，则：
$$\sum _{n=-\infty }^{\infty }{e}^{i2\pi n\Delta kx}=\sum _{n=-\infty }^{\infty }{e}^{i2\pi nu}=\sum _{m=-\infty }^{\infty }\delta (u-m)\text{\hspace{1em}(3)}$$

利用$\delta$函数的缩放性质$\delta (ax)=\frac{1}{|a|}\delta (x)$，可得：
$$\sum _{n=-\infty }^{\infty }{e}^{i2\pi n\Delta kx}=\frac{1}{\Delta k}\sum _{m=-\infty }^{\infty }\delta (x-\frac{m}{\Delta k})\text{\hspace{1em}(4)}$$

将式(4)代入式(1)，得到无限采样时的点扩散函数：
$$h_{\infty }(x)=\Delta k\cdot \frac{1}{\Delta k}\sum _{m=-\infty }^{\infty }\delta (x-\frac{m}{\Delta k})=\sum _{m=-\infty }^{\infty }\delta (x-\frac{m}{\Delta k})\text{\hspace{1em}(5)}$$

所以如果是无限采样下，只要确保$\Delta k$满足采样定律的要求，就可以完美复原图像，此时的点扩散函数正是周期重复的$\delta$函数。但是实践过程中，K空间的采样是不可能无限的，所以我们继续在有限采样的限制下继续推导：

式子(8.6)进一步简化可得：
$$h(x)=\Delta k\frac{\sin (\pi N\Delta kx)}{\sin (\pi \Delta kx)}{e}^{-i\pi \Delta kx}\text{\hspace{1em}(8.7)}$$

如果需要，采用从$-N/2$到$N/2$而不是从$-N/2$到$N/2-1$的对称$k$空间覆盖，就可以消除方程(8.7)中的相位项$e^{-i\pi \Delta kx}$。无论如何，与幅度项相比，其影响通常可以忽略不计。

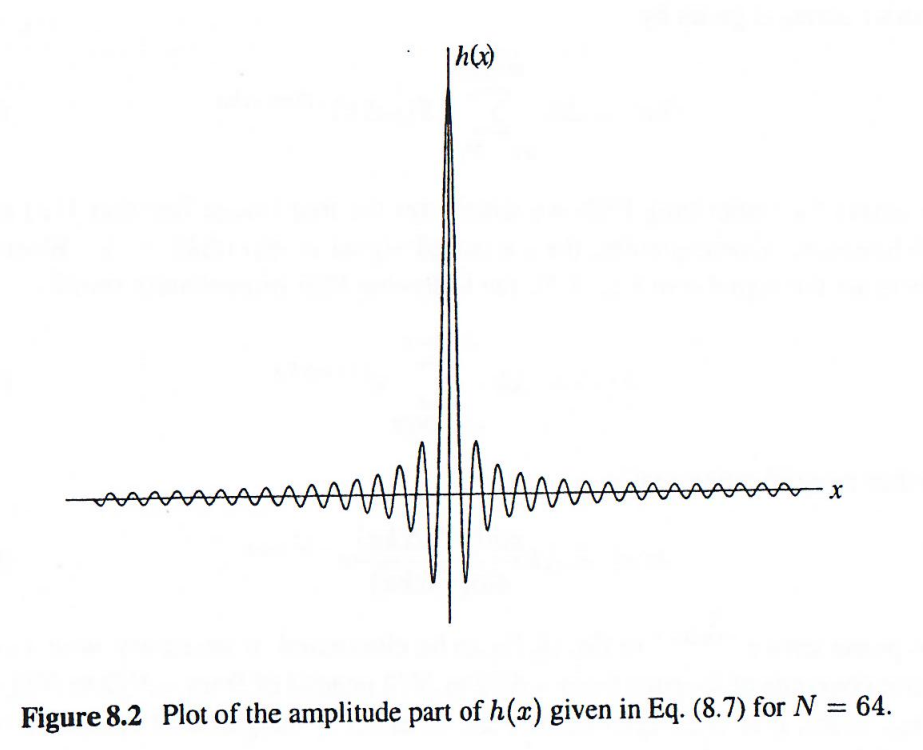
注意$h(x)$是一个周期函数，周期为$1/\Delta k$。$h(x)$在一个周期内的幅度部分见上图。从方程(8.7)可以确定，主瓣的宽度（由其两个零交叉点之间的间隔测量）为$2/(N\Delta k)$。$h(x)$的有效宽度，通过将积分限更改为覆盖$h(x)$的单个周期从方程(8.4)计算得出，由下式给出：
$$W_h=\frac{1}{h(0)}{\int }_{-1/(2\Delta k)}^{1/(2\Delta k)}h(x)dx=\frac{1}{N\Delta k}\text{\hspace{1em}(8.8)}$$

因此，$h(x)$的有效宽度正好是其主瓣宽度的一半。

• 方程(8.8)的右边被称为傅里叶像素大小：$\Delta x_F$，与通常的图像数字像素大小$\Delta x$形成对比。注意，$\Delta x$可以使用零填充或其他插值方案任意小，但图像分辨率基本限制在傅里叶像素大小。因此，为了使两个点源可区分，它们的间距必须大于$\Delta x_F$。

• 方程(8.8)的另一个含义是$W_h$和$N$不能同时减小。换句话说，我们不能同时提高图像分辨率和减少测量的数据点数。这一断言通常被称为傅里叶成像的不确定性关系，在实践中，人们选择$N$尽可能大，只要信噪比和成像时间允许。

这里有一个疑问，是否可以通过加大$\Delta k$，使得傅里叶像素变小呢？让我们回顾一下[[5.4 K空间采样 (Sampling of k-Space)]]里面提及的要求：

假设被成像的物体被一个宽度为 $W_x$ 和 $W_y$ 的矩形所限定，如下图所示。那么，根据采样定理，在$k$空间中的采样间隔需满足：
$$\Delta k_x\le \frac{1}{W_x}\text{和}\Delta k_y\le \frac{1}{W_y}\text{\hspace{1em}(5.122)}$$

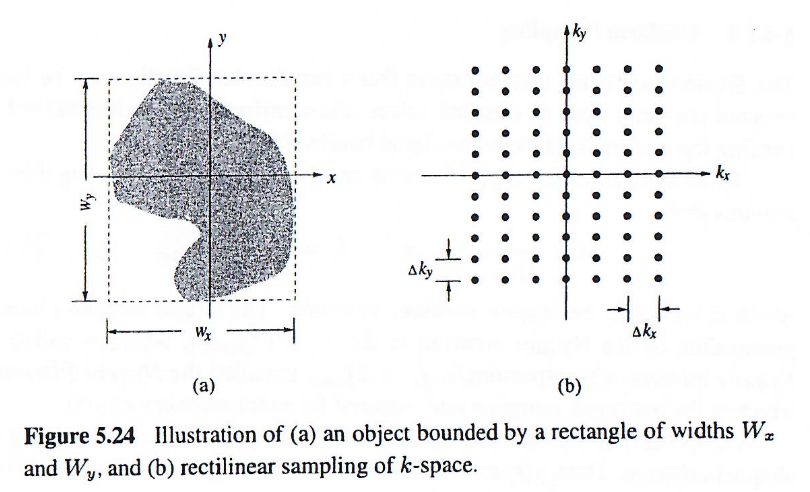
所以，$\Delta k$的大小是受限于成像物体大小的，不能任意的变大。换言之，一旦物体的尺寸确定了，其最大$\Delta k$也就确定了，此时成像的范围就确定了。这个时候，如果K空间采样的点数N越多，傅里叶像素也就越小。

小结：

• 有限K空间采样导致点扩散函数偏离$\delta$函数
• 确定好$\Delta k$后， K空间采样点数N越大，傅里叶像素大小越小，此时成像更不容易模糊（更接近真实物体）。

反投影重建的PSF

反投影重建的PSF由以下定理给出（后续再丰富一下内容）。

定理1 设$P(p,\varphi )$是二维函数$I(x,y)$的投影，$\hat{I}(x,y)$由下式给出：
$$\hat{I}(x,y)={\int }_0^{\pi }P(x\cos \varphi +y\sin \varphi ,\varphi )d\varphi \text{\hspace{1em}(8.9)}$$

则有：
$$\hat{I}(x,y)=I(x,y)\ast \ast \frac{1}{\sqrt{x^2+y^2}}\text{\hspace{1em}(8.10)}$$

其中$\ast \ast$表示二维卷积。

定理2 设$P(p,\theta ,\varphi )$是三维函数$I(x,y,z)$的投影，$\hat{I}(x,y,z)$由下式给出：
$$\hat{I}(x,y,z)=\frac{1}{2\pi }{\int }_0^{2\pi }{\int }_0^{\pi }P(x\sin \theta \cos \varphi +y\sin \theta \sin \varphi +z\cos \theta ,\theta ,\varphi )\sin \theta d\theta d\varphi \text{\hspace{1em}(8.11)}$$

则有：
$$\hat{I}(x,y,z)=I(x,y,z)\ast \ast \ast \frac{1}{\sqrt{x^2+y^2+z^2}}\text{\hspace{1em}(8.12)}$$

其中$\ast \ast \ast$表示三维卷积。

方程(8.10)表明二维反投影重建的PSF是：
$$h(x,y)=\frac{1}{\sqrt{x^2+y^2}}\text{\hspace{1em}(8.13)}$$

而根据方程(8.12)，三维反投影重建的PSF是：
$$h(x,y,z)=\frac{1}{\sqrt{x^2+y^2+z^2}}\text{\hspace{1em}(8.14)}$$

方程(8.13)可以通过考虑点源的投影如何被反投影以形成图像来推导。即，可以证明：
$${\int }_0^{\pi }\delta (x\cos \varphi +y\sin \varphi )d\varphi =\frac{1}{\sqrt{x^2+y^2}}\text{\hspace{1em}(8.15)}$$

方程(8.10)的更正式证明如下：
$$\begin{array}{rl}\hat{I}(x,y)& ={\int }_0^{\pi }P(x\cos \varphi +y\sin \varphi ,\varphi )d\varphi \\ & ={\int }_0^{\pi }{\int }_{-\infty }^{\infty }\mathcal{F}\rho (k,\varphi )e^{i2\pi k(x\cos \varphi +y\sin \varphi )}dkd\varphi \\ & ={\int }_0^{2\pi }{\int }_0^{\infty }\mathcal{F}\rho (k,\varphi )e^{i2\pi k(x\cos \varphi +y\sin \varphi )}dkd\varphi \\ & ={\int }_0^{2\pi }{\int }_0^{\infty }{k}^{-1}\mathcal{F}\rho (k,\varphi )e^{i2\pi k(x\cos \varphi +y\sin \varphi )}kdkd\varphi \\ & ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{k_x^2+k_y^2}}\mathcal{F}\rho (k_x,k_y)e^{i2\pi (x{k}_x+y{k}_y)}d{k}_{x}d{k}_y\\ & ={\mathcal{F}}^{-1}\left\{\frac{1}{\sqrt{k_x^2+k_y^2}}\right\}\ast \ast I(x,y)\\ & =I(x,y)\ast \ast \frac{1}{\sqrt{x^2+y^2}}\end{array}\text{\hspace{1em}(8.16)}$$

其中使用了以下恒等式：
$${\mathcal{F}}^{-1}\left\{\frac{1}{\sqrt{k_x^2+k_y^2}}\right\}=\frac{1}{\sqrt{x^2+y^2}}\text{\hspace{1em}(8.17)}$$

方程(8.12)可以证明如下。设$I(x,y,z)=\delta (x,y,z)$，则$P(p,\theta ,\varphi )=\delta (p)$。将其代入方程(8.11)得：
$$\begin{array}{rl}h(x,y,z)& =\frac{1}{2\pi }{\int }_0^{2\pi }{\int }_0^{\pi }\delta (x\sin \theta \cos \varphi +y\sin \theta \sin \varphi +z\cos \theta )\sin \theta d\theta d\varphi \\ & =\frac{1}{2\pi }{\int }_0^{2\pi }{\int }_0^{\pi }\delta (\mathbf{r}\cdot \mathbf{\mu })\sin \theta d\theta d\varphi \\ & =\frac{1}{2\pi |\mathbf{r}|}{\int }_0^{2\pi }{\int }_0^{\pi }\delta ({\mathbf{\mu }}_r\cdot \mathbf{\mu })\sin \theta d\theta d\varphi \end{array}\text{\hspace{1em}(8.18)}$$

其中$\mathbf{r}=(x,y,z)$，$\mathbf{\mu }=(\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta )$。由于问题的对称性，积分与${\mathbf{\mu }}_r$的方向无关。为简单起见，假设${\mathbf{\mu }}_r$沿$z$轴。则：
$$\begin{array}{rl}{\int }_0^{2\pi }{\int }_0^{\pi }\delta ({\mathbf{\mu }}_r\cdot \mathbf{\mu })\sin \theta d\theta d\varphi & ={\int }_0^{2\pi }{\int }_0^{\pi }\delta (\cos \theta )\sin \theta d\theta d\varphi \\ & =2\pi {\int }_{-1}^1\delta (x)dx\\ & =2\pi \end{array}$$

将此结果代入方程(8.18)立即得到：
$$h(x,y,z)=\frac{1}{|\mathbf{r}|}=\frac{1}{\sqrt{x^2+y^2+z^2}}\text{\hspace{1em}(8.19)}$$