当前位置：首页 > news >正文

小波自适应去噪在脑电信号处理MATLAB仿真实现

news 2025/11/16 11:20:04

1. 脑电信号特点与小波去噪原理

1.1 脑电信号特性

频率范围：0.5-100 Hz，主要能量集中在0.5-30 Hz
信号幅度：10-100 μV，非常微弱
噪声来源：
- 工频干扰：50/60 Hz电源干扰
- 肌电干扰：肌肉活动产生的高频噪声
- 眼电干扰：眨眼和眼球运动
- 基线漂移：低频成分
- 测量噪声：仪器本身噪声

1.2 小波去噪优势

时频局部化：能同时分析信号的时域和频域特征
多分辨率分析：适合分析非平稳的脑电信号
自适应特性：不同尺度采用不同阈值策略

2. 小波自适应去噪算法原理

2.1 基本流程

原始脑电信号 → 小波分解 → 系数阈值处理 → 小波重构 → 去噪后信号

2.2 关键算法步骤

步骤1：小波分解

选择合适的小波基函数和分解层数：
$[cAn,cDn,cDn−1,...,cD1]=DWT(EEG)[cA_n, cD_n, cD_{n-1}, ..., cD_1] = \text{DWT}(EEG)$
其中：

$cA_n$ ：第n层近似系数（低频）
$cD_k$ ：第k层细节系数（高频）

步骤2：阈值选择策略

1. 通用阈值（VisuShrink）

$λ=σ2ln⁡(N)\lambda = \sigma \sqrt{2\ln(N)}$

其中(\sigma)为噪声标准差，(N)为信号长度。

2. 自适应阈值（SURE Shrink）
基于Stein无偏风险估计，最小化均方误差。

3. 分层阈值
不同分解层采用不同阈值：

$λj=σj2ln⁡(N)j\lambda_j = \frac{\sigma_j \sqrt{2\ln(N)}}{\sqrt{j}}$

步骤3：阈值函数

硬阈值函数：
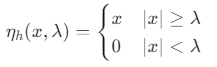
请添加图片描述

软阈值函数：
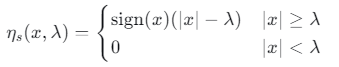
请添加图片描述

3. MATLAB仿真实现

3.1 完整的自适应去噪算法

%% 小波自适应去噪脑电信号仿真
clear; close all; clc;%% 参数设置
fs = 256;                    % 采样频率(Hz)
t = 0:1/fs:10-1/fs;          % 时间向量
N = length(t);               % 信号长度%% 生成模拟脑电信号（包含多种节律）
% 脑电节律成分
delta = 0.5 * sin(2*pi*2*t);          % Delta波 (1-4 Hz)
theta = 0.8 * sin(2*pi*6*t);          % Theta波 (4-8 Hz)  
alpha = 1.2 * sin(2*pi*10*t);         % Alpha波 (8-13 Hz)
beta = 0.6 * sin(2*pi*20*t);          % Beta波 (13-30 Hz)% 组合成纯净脑电信号
eeg_clean = delta + theta + alpha + beta;%% 添加各种噪声
% 1. 高斯白噪声（仪器噪声）
noise_white = 0.3 * randn(1, N);% 2. 工频干扰 (50Hz + 谐波)
noise_50hz = 0.5 * sin(2*pi*50*t) + 0.2 * sin(2*pi*100*t);% 3. 肌电干扰 (突发性高频噪声)
emg_noise = zeros(1, N);
emg_positions = [1000, 1500, 2000, 3500, 4000]; % 突发噪声位置
for pos = emg_positionsduration = 50; % 持续50个采样点idx = pos:min(pos+duration-1, N);emg_noise(idx) = 1.5 * randn(1, length(idx));
end% 4. 眼电干扰 (低频大幅值)
blink_noise = zeros(1, N);
blink_positions = [500, 1800, 3000];
for pos = blink_positionsduration = 100;idx = pos:min(pos+duration-1, N);blink_noise(idx) = 3 * (1 - cos(2*pi*(0:length(idx)-1)/duration));
end% 含噪脑电信号
eeg_noisy = eeg_clean + noise_white + noise_50hz + emg_noise + blink_noise;%% 小波自适应去噪函数
function eeg_denoised = wavelet_denoise_adaptive(eeg_signal, fs, wavelet_name, level)% 小波自适应去噪% 输入：eeg_signal - 含噪脑电信号%       fs - 采样频率%       wavelet_name - 小波名称%       level - 分解层数% 输出：eeg_denoised - 去噪后信号N = length(eeg_signal);% 小波分解[C, L] = wavedec(eeg_signal, level, wavelet_name);% 提取各层系数approx_coef = appcoef(C, L, wavelet_name, level);detail_coefs = cell(level, 1);for i = 1:leveldetail_coefs{i} = detcoef(C, L, i);end% 自适应阈值处理C_denoised = C; % 初始化去噪后系数% 对细节系数进行分层阈值处理start_idx = L(1) + 1;for i = 1:levelcoef_length = L(i+1);current_coef = C(start_idx:start_idx+coef_length-1);% 自适应阈值选择if i <= 2 % 高频层使用更严格的阈值threshold = thselect(current_coef, 'rigrsure'); % SURE阈值else % 低频层使用较宽松的阈值threshold = thselect(current_coef, 'heursure'); % 启发式阈值end% 软阈值处理（更好保留信号特征）denoised_coef = wthresh(current_coef, 's', threshold);% 更新系数C_denoised(start_idx:start_idx+coef_length-1) = denoised_coef;start_idx = start_idx + coef_length;end% 小波重构eeg_denoised = waverec(C_denoised, L, wavelet_name);% 确保长度一致if length(eeg_denoised) > Neeg_denoised = eeg_denoised(1:N);elseif length(eeg_denoised) < Neeg_denoised(end+1:N) = 0;end
end%% 执行小波去噪
wavelet_name = 'db4';    % Daubechies 4小波
level = 5;               % 分解层数eeg_denoised = wavelet_denoise_adaptive(eeg_noisy, fs, wavelet_name, level);%% 性能评估
% 信噪比计算
function snr_val = calculate_snr(clean_signal, noisy_signal)signal_power = mean(clean_signal.^2);noise_power = mean((noisy_signal - clean_signal).^2);snr_val = 10 * log10(signal_power / noise_power);
end% 均方根误差
function rmse_val = calculate_rmse(signal1, signal2)rmse_val = sqrt(mean((signal1 - signal2).^2));
end% 计算评估指标
snr_input = calculate_snr(eeg_clean, eeg_noisy);
snr_output = calculate_snr(eeg_clean, eeg_denoised);
rmse_before = calculate_rmse(eeg_clean, eeg_noisy);
rmse_after = calculate_rmse(eeg_clean, eeg_denoised);%% 时频分析函数
function [tfr, freq, time] = compute_stft(signal, fs, window_len, overlap)% 短时傅里叶变换window = hamming(window_len);noverlap = round(overlap * window_len);nfft = max(256, 2^nextpow2(window_len));[S, F, T] = spectrogram(signal, window, noverlap, nfft, fs);tfr = 20*log10(abs(S) + eps);freq = F;time = T;
end%% 结果可视化
figure('Position', [100, 100, 1400, 1000]);% 1. 时域信号对比
subplot(3,2,1);
plot(t, eeg_clean, 'b', 'LineWidth', 1.5); hold on;
plot(t, eeg_noisy, 'r', 'LineWidth', 0.5, 'Alpha', 0.7);
xlabel('时间 (s)'); ylabel('幅度 (\muV)');
title('原始脑电信号 vs 含噪信号');
legend('纯净信号', '含噪信号', 'Location', 'best');
grid on;subplot(3,2,2);
plot(t, eeg_clean, 'b', 'LineWidth', 1.5); hold on;
plot(t, eeg_denoised, 'g', 'LineWidth', 1.2);
xlabel('时间 (s)'); ylabel('幅度 (\muV)');
title('原始脑电信号 vs 去噪后信号');
legend('纯净信号', '去噪信号', 'Location', 'best');
grid on;% 2. 时频分析
window_len = 128; overlap = 0.75;% 纯净信号时频图
subplot(3,2,3);
[tfr_clean, freq_clean, time_clean] = compute_stft(eeg_clean, fs, window_len, overlap);
imagesc(time_clean, freq_clean, tfr_clean);
axis xy; colorbar; clim([-20 40]);
xlabel('时间 (s)'); ylabel('频率 (Hz)');
title('纯净信号时频图');% 含噪信号时频图
subplot(3,2,4);
[tfr_noisy, freq_noisy, time_noisy] = compute_stft(eeg_noisy, fs, window_len, overlap);
imagesc(time_noisy, freq_noisy, tfr_noisy);
axis xy; colorbar; clim([-20 40]);
xlabel('时间 (s)'); ylabel('频率 (Hz)');
title('含噪信号时频图');% 去噪信号时频图
subplot(3,2,5);
[tfr_denoised, freq_denoised, time_denoised] = compute_stft(eeg_denoised, fs, window_len, overlap);
imagesc(time_denoised, freq_denoised, tfr_denoised);
axis xy; colorbar; clim([-20 40]);
xlabel('时间 (s)'); ylabel('频率 (Hz)');
title('去噪后信号时频图');% 3. 性能指标显示
subplot(3,2,6);
text(0.1, 0.9, sprintf('输入信噪比: %.2f dB', snr_input), 'FontSize', 12);
text(0.1, 0.7, sprintf('输出信噪比: %.2f dB', snr_output), 'FontSize', 12);
text(0.1, 0.5, sprintf('SNR改善: %.2f dB', snr_output - snr_input), 'FontSize', 12);
text(0.1, 0.3, sprintf('RMSE (去噪前): %.4f', rmse_before), 'FontSize', 12);
text(0.1, 0.1, sprintf('RMSE (去噪后): %.4f', rmse_after), 'FontSize', 12);
axis off;
title('去噪性能指标');%% 不同小波基函数比较
wavelets = {'db4', 'sym4', 'coif3', 'bior3.3'};
snr_improvements = zeros(1, length(wavelets));
rmse_results = zeros(1, length(wavelets));fprintf('=== 不同小波基函数性能比较 ===\n');
for i = 1:length(wavelets)eeg_temp = wavelet_denoise_adaptive(eeg_noisy, fs, wavelets{i}, level);snr_temp = calculate_snr(eeg_clean, eeg_temp);rmse_temp = calculate_rmse(eeg_clean, eeg_temp);snr_improvements(i) = snr_temp - snr_input;rmse_results(i) = rmse_temp;fprintf('小波基: %s, SNR改善: %.2f dB, RMSE: %.4f\n', ...wavelets{i}, snr_improvements(i), rmse_temp);
end%% 绘制不同小波性能比较图
figure('Position', [200, 200, 1000, 400]);
subplot(1,2,1);
bar(snr_improvements, 'FaceColor', [0.2 0.6 0.8]);
set(gca, 'XTickLabel', wavelets);
ylabel('SNR改善 (dB)');
title('不同小波基函数的SNR改善');
grid on;subplot(1,2,2);
bar(rmse_results, 'FaceColor', [0.8 0.4 0.2]);
set(gca, 'XTickLabel', wavelets);
ylabel('RMSE');
title('不同小波基函数的RMSE');
grid on;

3.2 高级自适应算法扩展

%% 基于小波包的自适应去噪（更精细的频率划分）
function eeg_denoised_wp = wavelet_packet_denoise(eeg_signal, wavelet_name, level)% 小波包去噪 - 提供更精细的频带划分% 小波包分解wp = wpdec(eeg_signal, level, wavelet_name);% 计算最佳基（使用熵准则）entropy_type = 'shannon';wp_best = bestbas(wp, entropy_type);% 节点阈值处理for i = 0:(2^level - 1)node_coef = wpcoef(wp_best, [level, i]);if ~isempty(node_coef)% 自适应阈值threshold = thselect(node_coef, 'rigrsure');denoised_coef = wthresh(node_coef, 's', threshold);% 更新系数wp_best = write(wp_best, 'cfs', [level, i], denoised_coef);endend% 小波包重构eeg_denoised_wp = wprec(wp_best);
end%% 执行小波包去噪
eeg_wp_denoised = wavelet_packet_denoise(eeg_noisy, 'db4', 4);% 比较性能
snr_wp = calculate_snr(eeg_clean, eeg_wp_denoised);
fprintf('\n小波包去噪性能: SNR = %.2f dB\n', snr_wp);

4. 实际脑电信号处理应用

4.1 真实脑电数据处理建议

%% 实际脑电数据处理流程
function processed_eeg = process_real_eeg(eeg_data, fs, channels)% 实际脑电信号处理流程% 输入：eeg_data - 多通道脑电数据%       fs - 采样率%       channels - 要处理的通道索引[num_channels, num_samples] = size(eeg_data);processed_eeg = zeros(length(channels), num_samples);for i = 1:length(channels)ch_idx = channels(i);raw_signal = eeg_data(ch_idx, :);% 1. 预处理：去除基线漂移baseline = medfilt1(raw_signal, fs); % 中值滤波估计基线signal_detrend = raw_signal - baseline;% 2. 工频陷波 (50Hz)wo = 50/(fs/2);  bw = wo/35;[b,a] = iirnotch(wo, bw);signal_notched = filtfilt(b, a, signal_detrend);% 3. 小波自适应去噪signal_denoised = wavelet_denoise_adaptive(signal_notched, fs, 'db4', 5);processed_eeg(i, :) = signal_denoised;end
end