预测汽车燃油效率——线性回归
问题:预测汽车重量=2.32时,每加仑燃油行驶的英里数是多少
汽车重量与燃油效率数据表
| 汽车重量(千磅) | 每加仑燃油行驶的英里数(标签) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
| 2.32 | ? |
汽车重量与燃油效率图
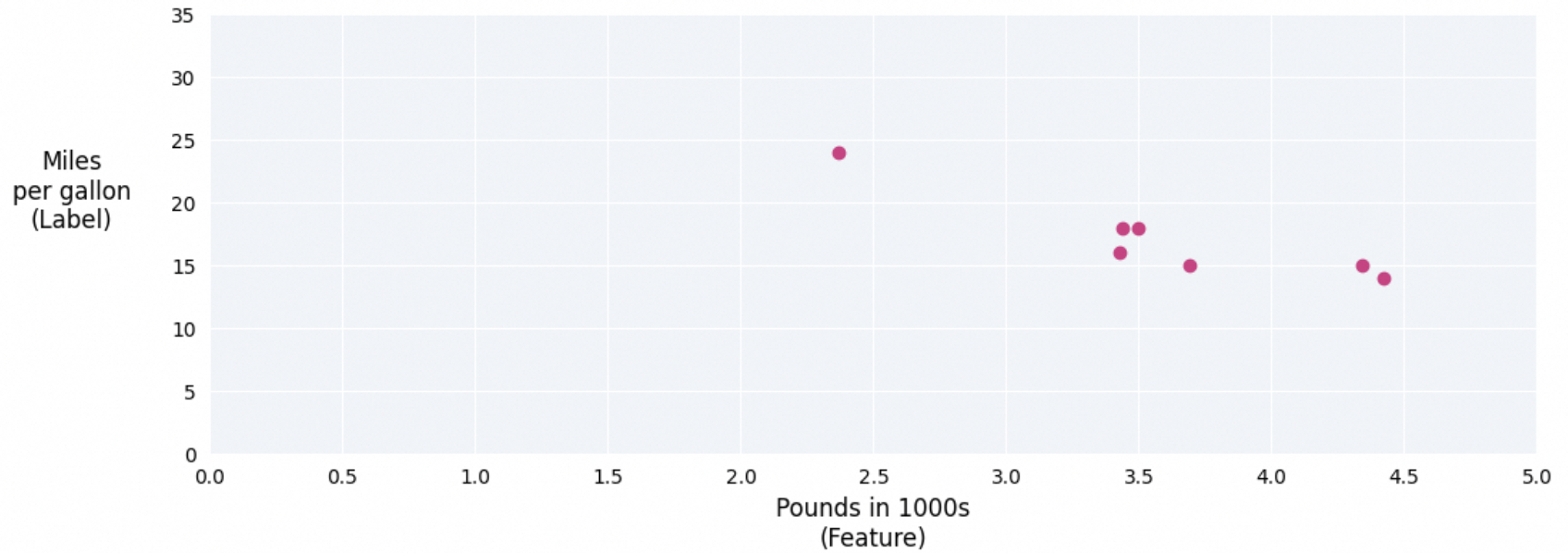
绘制一条最佳拟合线
这条直线使得,样本数据离直线距离之和最短。这样我们便知道x=2.32时,y的值。
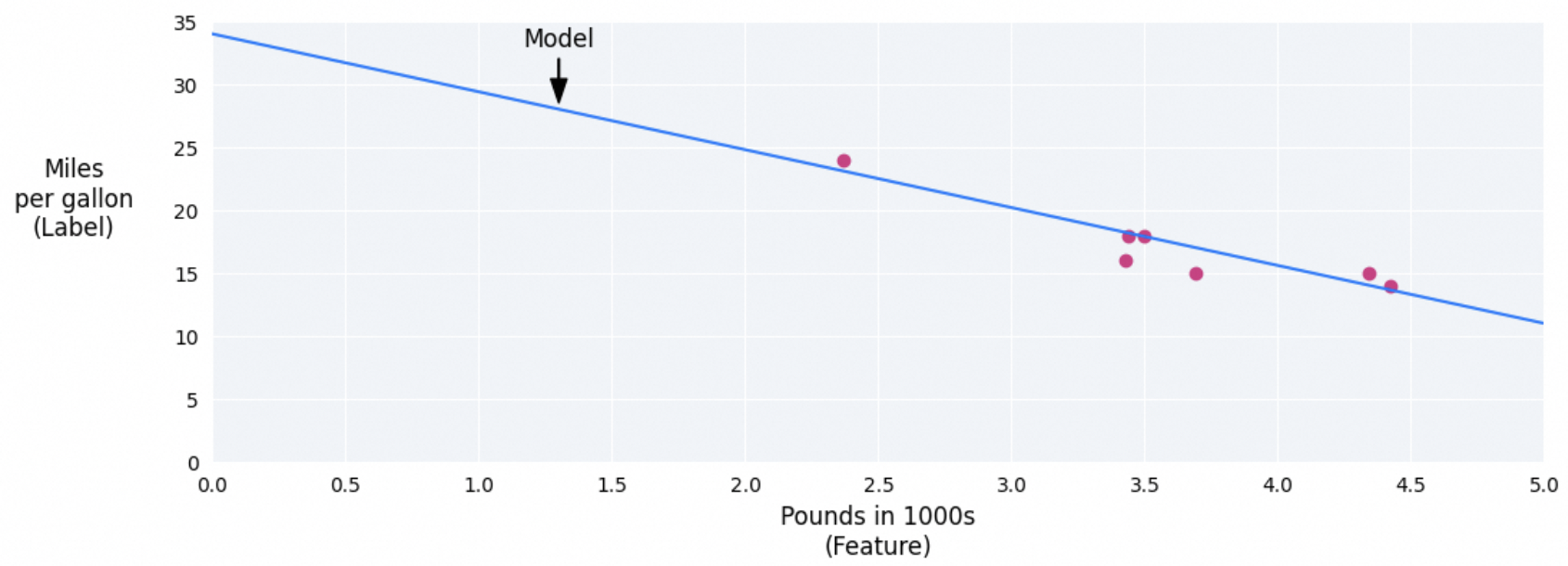
线性方程【直线方程】
也就是找到这样一个线性方程
y=kx+b y=kx+b y=kx+b
如何找到这个线性方程
实际值与预测值的差值图
使用实际值与预测值的差值来评判是不是最适合的直线:
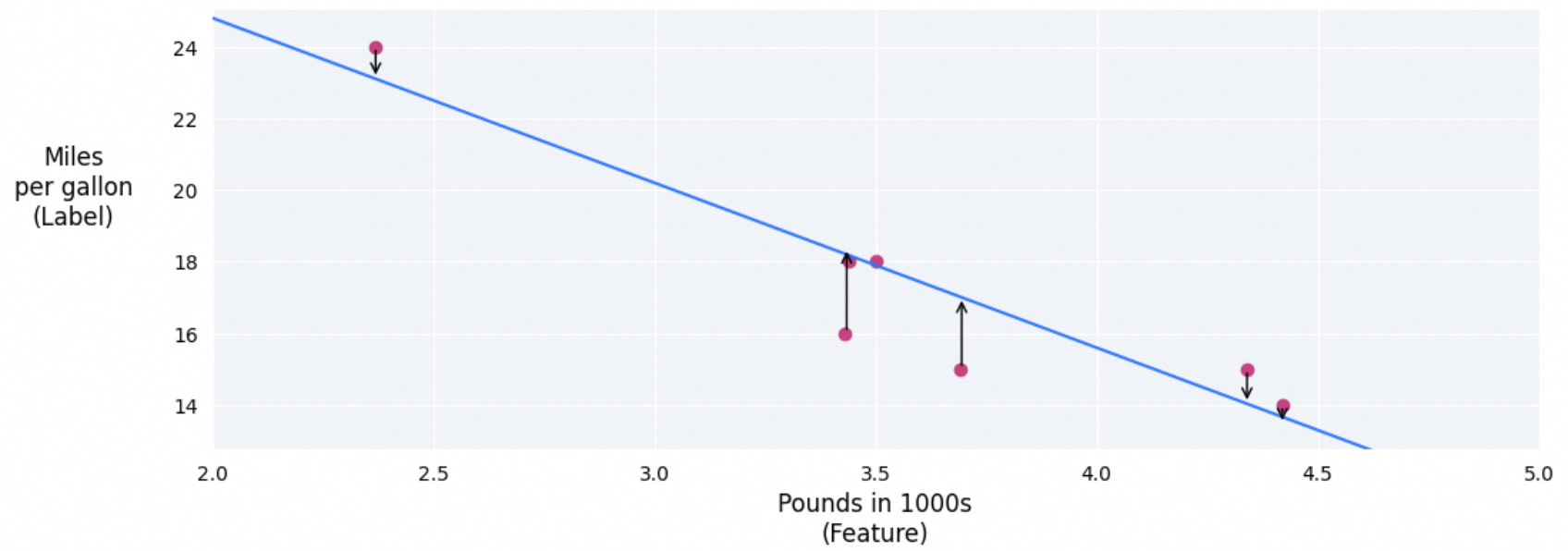
5种评判方法
| 指标名称 | 白话公式 | 数学公式 | 特点 |
|---|---|---|---|
| 绝对值误差之和(SAE) | 求和∣实际值−预测值∣ 求和 |实际值- 预测值| 求和∣实际值−预测值∣ | ∑∣yi−y^i∣ \sum |y_i - \hat{y}_i| ∑∣yi−y^i∣ | 抗异常值,但未标准化 |
| 平均绝对误差(MAE) | 1n(求和|实际值−预测值|) {\frac{1}{n} (求和|实际值 - 预测值|)} n1(求和|实际值−预测值|) | 1n∑∣yi−y^i∣ \frac{1}{n} \sum |y_i - \hat{y}_i| n1∑∣yi−y^i∣ | 直观易懂,单位一致 |
| 误差平方和(SSE) | 求和(实际值−预测值)2 求和 (实际值 - 预测值)^2 求和(实际值−预测值)2 | ∑(yi−y^i)2 \sum (y_i - \hat{y}_i)^2 ∑(yi−y^i)2 | 放大大误差,用于优化算法 |
| 均方误差(MSE) | 1n(求和(实际值−预测值)2) \frac{1}{n} (求和 (实际值 - 预测值)^2 )n1(求和(实际值−预测值)2) | 1n∑(yi−y^i)2 \frac{1}{n} \sum (y_i - \hat{y}_i)^2 n1∑(yi−y^i)2 | 对大误差敏感,值非负 |
| 均方根误差(RMSE) | 1n∑(实际值−预测值)2 \sqrt{\frac{1}{n} \sum (实际值 - 预测值)^2} n1∑(实际值−预测值)2 | 1n∑(yi−y^i)2 \sqrt{\frac{1}{n} \sum (y_i - \hat{y}_i)^2} n1∑(yi−y^i)2 | 单位一致,平衡误差惩罚 |
转化问题
🌱 第一步:问题是什么?
你有一组数据:汽车重量(x)和油耗(y)。你想找一条直线:
y^=w⋅x+b \hat{y} = w \cdot x + b y^=w⋅x+b
使得这条直线能尽可能准确地预测 y。
比如:
- 当 x = 3.5(千磅),真实 y = 18
- 如果模型预测 y^=10\hat{y}=10y^=10,那就差了 8,不好
- 如果预测 y^=17.9\hat{y}=17.9y^=17.9,那就很好
所以,我们需要一个衡量“好不好”的标准 → 这就是损失函数。
📉 第二步:如何确定是这条直线预测准
1.选择均方误差
当然也可以选择其他误差方式,根据实际问题的场景不同,可以选择不同,这里先选定是均方差。这就是经验了。
推荐一本书解释了这个思想,刘雪峰的《心中有数 生活中的数学思维》【第13章 “执两用中”的智慧】
2.均方误差公式:
a.白话公式:
1n(求和(实际值−预测值)2) \frac{1}{n} (求和 (实际值 - 预测值)^2 )n1(求和(实际值−预测值)2)
b.数学公式:
1n∑(yi−y^i)2 \frac{1}{n} \sum (y_i - \hat{y}_i)^2 n1∑(yi−y^i)2
注意:
- ∑\sum∑ 表示求和
- yiy_iyi 表示实际值
- y^i\hat{y}_iy^i 表示预测值
- 1n∑(yi−y^i)2\frac{1}{n} \sum (y_i - \hat{y}_i)^2n1∑(yi−y^i)2 表示每个样本实际值减去预测值的平方相加,再除以样本数,即平均平方误差
3.损失函数
所以上面的公式就是损失函数,即损失函数为:
损失L=1n∑(yi−y^i)2 损失L=\frac{1}{n} \sum (y_i - \hat{y}_i)^2 损失L=n1∑(yi−y^i)2
说明:
- yiy_iyi是真实值(比如 18)
- yi=wxi+by_i = wx_i + byi=wxi+b是模型预测值
- 平方是为了让正负误差都变成正数,且大误差惩罚更重
👉 关键理解:
L 是 w 和 b 的函数。xix_ixi 和 yiy_iyi 是已知常数(数据),只有 w 和 b 是变量。
所以我们可以写成:
L(w,b)=1n∑i=1n(yi−(wxi+b))2L(w,b) = \frac{1}{n}\sum_{i=1}^{n}(y_i - (wx_i + b))^2L(w,b)=n1i=1∑n(yi−(wxi+b))2
我们的目标:找到一组 w 和 b,让 L(w, b) 最小。
❓ 问题:怎么找让 L 最小的 w 和 b?
如果我现在用某个 w 和 b(比如 w=0, b=0),我能不能知道“稍微改一点 w 或 b,L 会变大还是变小”?
如果能知道,我们就可以系统地调整 w 和 b,让 L 越来越小。
这就是关键!
🔍 核心思想:看“变化率”
待补充:斜率、导数
第一步:明确目标
我们希望:新的损失比原来小 → 即 ΔL < 0
(因为 ΔL = 新L − 旧L,所以 ΔL < 0 意味着损失变小了)
