LeetCode hot100:142 环形链表 II:寻找环的入口节点
问题描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。进阶:你是否可以使用 O(1) 空间解决此题?
不允许修改 链表。
示例1:
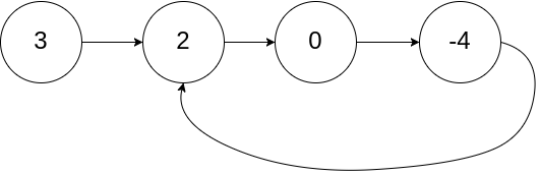
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例2:
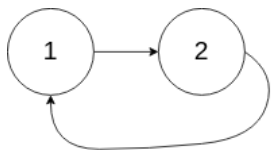
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例3:
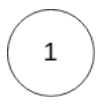
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
解决方法:
方法一:哈希表法
算法思路:
遍历链表中的每个节点,并将节点引用存储在哈希集合中。如果当前节点已经存在于集合中,则说明该节点就是环的入口;如果遍历到 null,则说明链表无环。
算法步骤:
-
初始化一个空的哈希集合
-
遍历链表中的每个节点:
-
如果当前节点已在集合中,返回该节点(环的入口)
-
否则将当前节点加入集合
-
移动到下一个节点
-
-
如果遍历到
null,返回null(无环)
代码实现:
class Solution:def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:visited = set()current = headwhile current:if current in visited:return currentvisited.add(current)current = current.nextreturn None复杂度分析:
- 时间复杂度:O(n),其中 n 是链表中的节点数
- 空间复杂度:O(n),最坏情况下需要存储所有节点
方法二:快慢指针
算法思路:
使用两个指针,快指针每次移动两步,慢指针每次移动一步。如果存在环,快慢指针必定会相遇。相遇后,将一个指针重置到链表头部,两个指针都以每次一步的速度移动,再次相遇的节点就是环的入口。
算法步骤:
-
初始化快慢指针都指向头节点
-
使用循环让快指针每次走两步,慢指针每次走一步:
-
如果快指针遇到
null,说明无环,返回null -
如果快慢指针相遇,说明有环
-
-
将快指针重置到头节点
-
快慢指针都以每次一步的速度移动,直到再次相遇
-
返回相遇节点(环的入口)
代码实现:
class Solution:def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:if not head or not head.next:return None# 判断是否有环fast = slow = headwhile fast and fast.next:fast = fast.next.nextslow = slow.next# 从链表头部到环入口的距离a,等于从相遇点走c步,再加上k-1圈环的长度。if slow == fast:fast = headwhile fast != slow:fast = fast.nextslow = slow.nextreturn fastreturn None复杂度分析:
- 时间复杂度:O(n),其中 n 是链表中的节点数
- 空间复杂度:O(1),只使用了常数级别的额外空间
问题详解:
为什么快慢指针可以找到环的入口?
原理推导:假设
-
a:链表头部到环入口的距离 -
b:环入口到相遇点的距离 -
c:相遇点到环入口的距离 -
环的长度:L = b + c
当快慢指针第一次相遇时:慢指针走了 a + b 的距离,快指针走了 a + b + k ( b + c ),其中 k 是快指针在环中走的圈数。
由于快指针速度是慢指针二倍,则存在:a + b + k ( b + c ) = 2(a + b),整理得
a = (k - 1)(b + c)+ c
说明:从链表头部到环入口的距离 a,等于从相遇点走 c 步,再加上 k-1 圈环的长度。故将一个指针重置到头部,两个指针都以相同速度前进时,它们会在环入口处相遇。
总结:
在方法二中,函数返回的是 节点x 这个对象
| 方法 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|
| 哈希表法 | 思路简单直观 | 需要O(n)额外空间 | 对空间要求不高的场景 |
| 快慢指针 | 空间复杂度O(1) | 理解难度稍大 | 对空间有严格限制的场景 |
推荐使用快慢指针法,因为它满足题目"不允许修改链表"的要求,并且空间复杂度最优。这种方法体现了双指针技巧的巧妙运用,是解决链表环相关问题的经典算法。
