字符串匹配和回文串类题目
暴力算法
如果刚开始学习字符串匹配，那么最容易想到的算法就是暴力，
一旦找到相同的开头我就看看这个字符串能不能与主串后面的字符匹配上
比如：
如果匹配不上，直接返回到刚开始头部字母的下一位继续匹配就好了
但是不难发现，假如你要匹配的字符串是aac，但是主串是aaaaaaaaaaaaaaac
显然，这样每次c匹配不上就回溯，明明已经知道前面的a不可能匹配上后面的c，但是依然要回溯
这使得在一些情况下程序执行的时间特别长
有没有一种办法，一次就可以遍历完成不回溯？
有的兄弟，有的，这个方法就是kmp算法
KMP算法
kmp算法的本质就是告诉你下一次退回到哪个位置可以和主串的下一个字符进行比较最省事
比如：主串是ababcababa 子串是ababa
正常情况下，根据暴力算法，一旦匹配不上你就得回溯，这相当浪费时间
但是kmp告诉我们，你不用回退，继续往前比较就行
那kmp算法怎么知道当ababa的最后一个a匹配不上时，该回退到哪一步继续比较
这就涉及到了kmp算法的核心也就是next数组
有人又称作fail数组或者pi数组，不过不管叫什么，这个数组的作用就是告诉你假如不回退，下一步谁和谁进行比较
在手动实现next数组的过程中，其对应的值经常被称作当前位置前后缀字符串相等的最长长度
比如abcdeabcd：其 最长 相等长 前后缀 长度就是4 a b c d e a b c d
通常头尾是不被计入的，
比如：a，只有一个字母，既是开头也是结尾，所以其 最长 相等长 前后缀 长度就是0
又比如：aaaaaa,头尾不被计入,所以其 最长 相等长 前后缀 长度就是5,分别是前5个a和后五个a
因此假如有一个字符串：a b c d e a b c d
根据上述规则得到其next数组，
当指针指向a时，只有一个字母，既是开头也是结尾，所以其 最长 相等长 前后缀 长度就是0
当指针指向b时，ab没有相同前后缀，所以其 最长 相等长 前后缀 长度也是0
.........
当指针指向第二个a时，这个a和第一个a恰好是一头一尾，这里的头尾和一开始说的头尾并不相同
一开始不计入的头尾是这样的，这里的红色字母通常不算
但是这里的绿色字母要算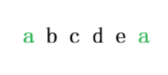
因此此时其 最长 相等长 前后缀 长度就是1
以此类推得到
当然这个next数组的写法不尽相同，有的习惯全部-1，有的人习惯右移1位，这些都是按照后面的匹配规则来的，都是正确的，甚至还有升级版的nextval数组，这里就不提了
（下面的所有代码都是按照最初始的next数组来实现）
那么计算机如何实现next数组，从
我们可以找到一点规律，当a第二次出现时，a对应的next数组值恰好是a第一次出现的下一个位置
也就是告诉我们下一步6号b得和1号b进行比较
于是我们得到结论：当两个字符相匹配时，指向两个正在比较字符的指针都可以向左移动一步
那遇到不相等的字符呢，那只能选择回退知道遇上匹配的字符或者退回到了最开始的位置
这里很难描述清楚，跟着代码走一遍会更清楚
详细描述参考https://blog.csdn.net/shenghaide_jiahu/article/details/146333525?fromshare=blogdetail&sharetype=blogdetail&sharerId=146333525&sharerefer=PC&sharesource=shenghaide_jiahu&sharefrom=from_link
于是有如下代码：
第一个循环用于计算next数组，第二个循环用于查找
class Solution {
public:int strStr(string haystack, string needle) {vector<int>next(needle.size(),0);for(int i=1,j=0;i<needle.size();i++){while(j>0&&needle[i]!=needle[j]){j=next[j-1];}if(needle[i]==needle[j])j++;next[i]=j;}for(int i=0,j=0;i<haystack.size();i++){while(j>0&&haystack[i]!=needle[j]){j=next[j-1];}if(haystack[i]==needle[j])j++;if(j==needle.size())return i+1-j;}return -1;}
};
kmp算法的高级应用
class Solution {
public:int repeatedStringMatch(string a, string b) {int la=a.size(),lb=b.size(),rep=1;if(lb==0)return 0;vector<int>next(lb);for (int i=1, j=0; i < lb; ++i) {while (j && b[i] != b[j]) j = next[j - 1];if (b[i] == b[j]) ++j;next[i] = j;}for(int i=0,j=0;i<lb+2*la;i++){while(j &&a[i%la]!=b[j])j=next[j-1];if(a[i%la]==b[j])j++;if(j==lb)return ceil((i+1)/double(la));}return -1;}
};这道题的完整代码如上：
首先由于题目类型依旧是字符串匹配，所以我们还是计算出next数组，代码和第一题一模一样
比较不同的是第二点，题目是叠加字符串，在叠加的字符串里面找到目标子串，但是显然，不能盲目生成主串，我们得考虑一下主串大概有多长，
就以这个为例
，cdabcdab，出去中间的倍数完整部分之外，左右还各有一节可能完整可能不完整的字符串，cd abcd ab
因此最长最长主串不会超过b的长度加上2a的长度，也就是在b两头各补充一个a
同时为节省空间，我们利用叠加性质以及取余技巧，abcd下一个字符必定是a
于是巧妙地在不生成主串的情况下完成了比较
最后别忘了i+1才是主串的长度，而且要对上取整保证叠加串是包含了b串的
回文数
回文数类的题目看起来和前后缀相同没啥关系但是依然可以巧妙用上kmp算法
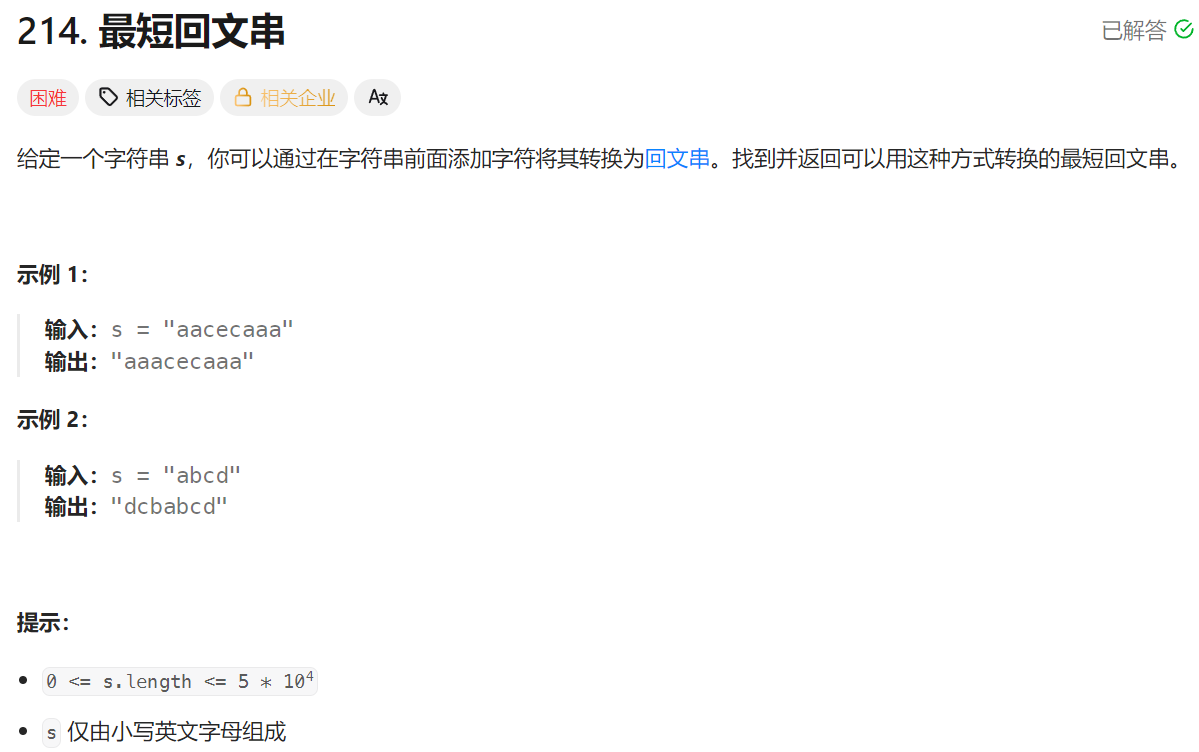
这里题目说白了就是找到从开头开始算最长的回文串，因为叠加的越长，整体就会越短
那如何找到这样的最长回文串呢，其实也是匹配！
由于回文串具有颠倒后顺序不变的性质，于是我们可以尝试将原来的字符串颠倒
我们发现颠倒后绿框内的字符串仍然能够保持相等，所以这个字符串就是最长的回文串
我查找了好多资料都没有说清楚这个到底是怎么匹配的
后面我发现匹配过程其实和next数组的计算过程类似，
next数组的计算中，以abcdabcdeabc为例，
我们可以找到开头的abc与d之后的abc是abcdabc的相同前后缀，
虽然不是回文关系但是有一定的关联，
当这个字符串走到末尾我们就发现首尾相同的字符串是abc，
也就是说当next数组执行完毕，我们就知道了首尾字符串的最长相同长度，
而一开始我们要找的恰好也就是原来字符串，以及反转后字符串，首尾字符串的最长相同长度，
所以这个题目其实就是调用了两次计算next数组的for循环
代码如下：
class Solution{
public:string shortestPalindrome(string s) {vector<int>next(s.size(),0);for(int i=1,j=0;i<s.size();i++){while(j&&s[i]!=s[j]){j=next[j-1];}if(s[i]==s[j]){j++;}next[i]=j;}int j=0;for(int i=s.size()-1;i>=0;i--){while(j&&s[i]!=s[j]){j=next[j-1];}if(s[i]==s[j]){j++;}}string add = s.substr(j);reverse(add.begin(),add.end());return add+s;}
};当然这里和描述的不一样，因为为节省空间，我们可以倒序遍历来代替字符串反转，更快更省空间
此时最后一个字符对应的数字即为最长长度，然后用substr提取后半段非回文字符串，反转后拼到s之前即可，这个题目还是比较绕的，需要对kmp以及next数组的理解比较深入
动态规划
在思考kmp算法时，我发现后面的数据并不会干扰之前计算的结果，且总是需要保存之前计算的结果，这不就是动态规划的模板吗，于是我思考用动态规划做这一类回文数的题目；
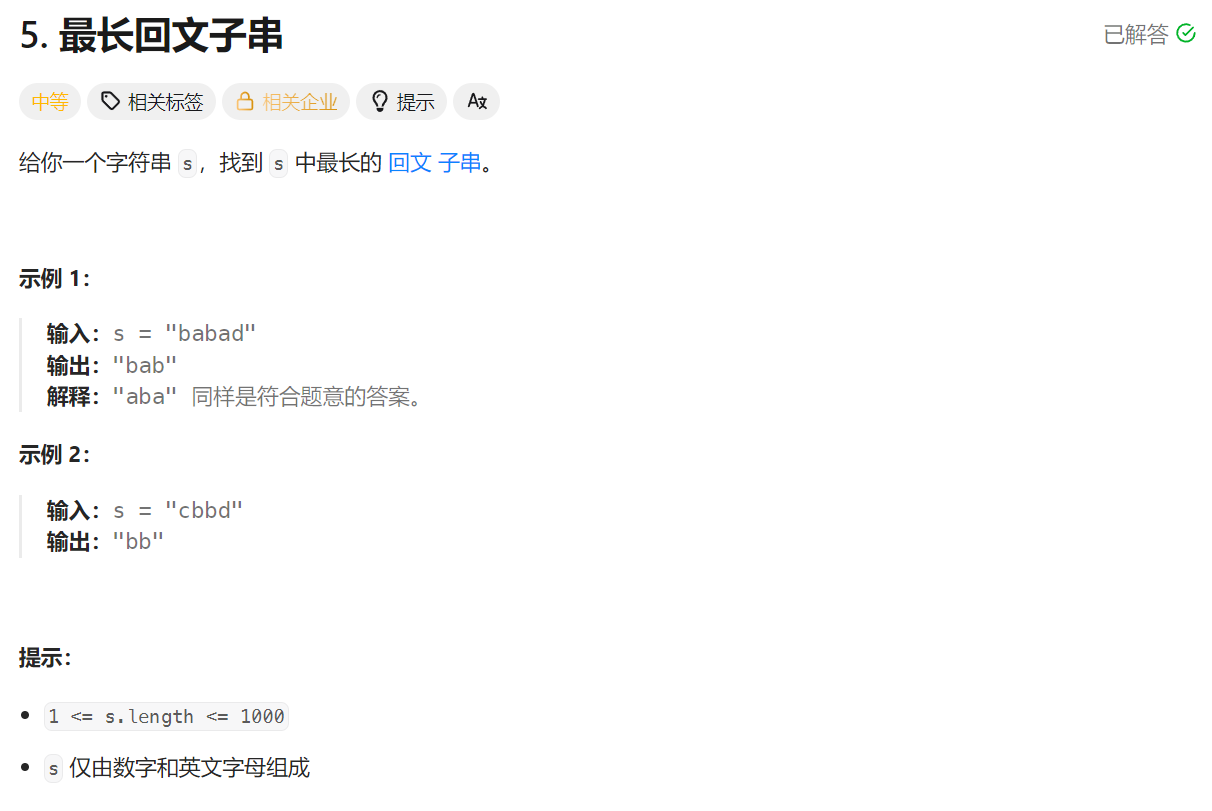
class Solution {
public:string longestPalindrome(string s) {vector<vector<int>>dp(s.size()+1,vector<int>(s.size()+1,0));for(int i=0;i<s.size();i++)dp[i][i]=1;int maxi=0,maxj=0;for(int i=s.size()-2;i>=0;i--){for(int j=i+1;j<s.size();j++){if(s[i]==s[j]&&((j-i)==1||dp[i+1][j-1]>0)){dp[i][j]=j==i+1?2:dp[i+1][j-1]+2;}if(dp[i][j]>dp[maxi][maxj]){maxi=i;maxj=j;}}}return s.substr(maxi,maxj-maxi+1);}
};动态规划的核心是寻找状态状态转移方程
我们发现这其中有以下状态
当i==j时，也就是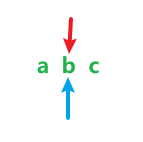
，此时dp[i][j]=1;
当i==j-1时，也就是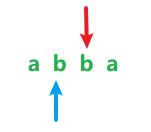
，此时假如s[i]==s[j],dp[i][j]=2;否则dp[i][j]=0（保持不变）
当j-i>=2时，也就是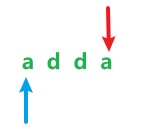
，此时假如s[i]==s[j],dp[i][j]=dp[i+1][j-1]+2;否则dp[i][j]=0（保持不变）
tips:
(1)这里我们一开始就把所有i==j的情况全部记作1，可以减少讨论
(2)i的获得依赖于i+1,且j的获得依赖于j-1，且j总是大于i
因此一定要注意循环开始和结束的条件，i是从s.size()-2开始逆序，j从i+1开始正序
关于空间的优化：一维滚动数组
class Solution {
public:int countSubstrings(string s) {int ans=s.size();vector<int>dp(s.size(),0);for(int i=s.size()-2;i>=0;i--){dp[i+1]=1;for(int j=s.size()-1;j>i;j--){if(s[i]==s[j]&&(j==i+1||dp[j-1]>0)){dp[j]=j==i+1?2:dp[j-1]+2;ans++;}else{dp[j]=0;}}}return ans;}
};这里一定要都是倒序遍历，防止污染数据
其实还是根据dp这里的定义来的，j的上一级数据总是来自j-1，因此只能从右侧往左侧更新，防止污染左侧上次循环留下的数据
注意一定要刷新数据，且每次开始时记得更新i==j的情况，总的来说就是比较麻烦
关于时间的优化：Manacher算法
class Solution {
public:int countSubstrings(string s) {int n = s.size();string t = "$#";for (const char &c: s) {t += c;t += '#';}n = t.size();t += '!';auto f = vector <int> (n);int iMax = 0, rMax = 0, ans = 0;for (int i = 1; i < n; ++i) {// 初始化 f[i]f[i] = (i <= rMax) ? min(rMax - i + 1, f[2 * iMax - i]) : 1;// 中心拓展while (t[i + f[i]] == t[i - f[i]]) ++f[i];// 动态维护 iMax 和 rMaxif (i + f[i] - 1 > rMax) {iMax = i;rMax = i + f[i] - 1;}// 统计答案, 当前贡献为 (f[i] - 1) / 2 上取整ans += (f[i] / 2);}return ans;}
};作者：力扣官方题解
链接：https://leetcode.cn/problems/palindromic-substrings/solutions/379987/hui-wen-zi-chuan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。这个算法较复杂，可以参考leetcode的官方题解
最后还有个中心扩散算法，这个是最省空间的，同时算法本身比较简单，也在leetcode的官方题解中