Diffusion VS Flow Matching

目录

Diffusion

前向过程

逆向过程

优化目标

DDIM

前向过程

逆向过程

Flow Matching

训练

推理

---

        在生成模型领域，‌Diffusion ‌和‌Flow Matching‌是两种重要的生成方法，它们在建模数据分布和样本生成上有不同的技术路径。

        Flow Matching 和Diffusion是很像的，很多时候是等价的。比如，Flow Matching使用Euler的采样等价于使用DDIM采样器的Diffusion。

Diffusion

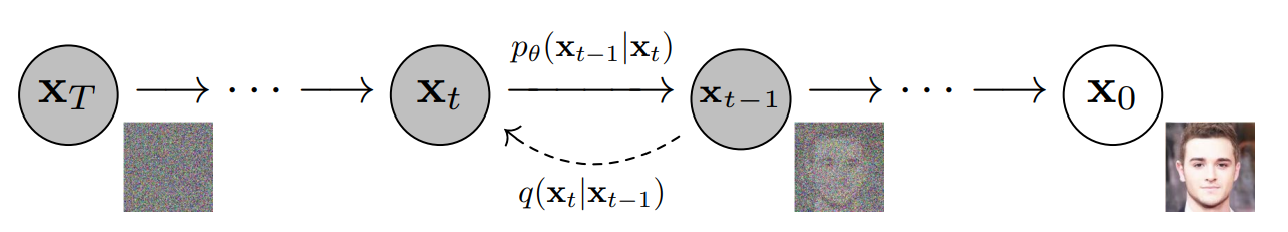
前向过程

         前向过程是加噪的过程，从𝑥0 到 𝑥𝑇 ，逐步加噪至一组纯噪声图片。添加的噪声是已知的{𝛽1，𝛽2，...，𝛽𝑇}，不同的t，不同的噪声，且随着t的增加逐渐增大，满足𝛽1<𝛽2<...<𝛽𝑇。

        前向过程中图像𝑥𝑡只和上一时刻的𝑥𝑡−1有关, 该过程可以视为马尔科夫过程, 满足:

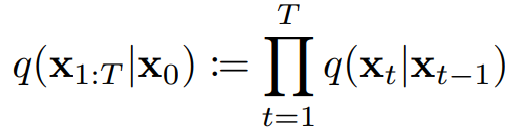
q(𝑥1:𝑇|𝑥0)表示从原始图像 𝑥10 开始，经过 𝑇步加噪过程后得到噪声图像 𝑥𝑇 的概率分布。q(𝑥𝑡|𝑥𝑡−1)是条件概率分布，已知𝑥𝑡−1，得到𝑥𝑡的概率分布，这是一个高斯分布，其均值为 ，方差为。

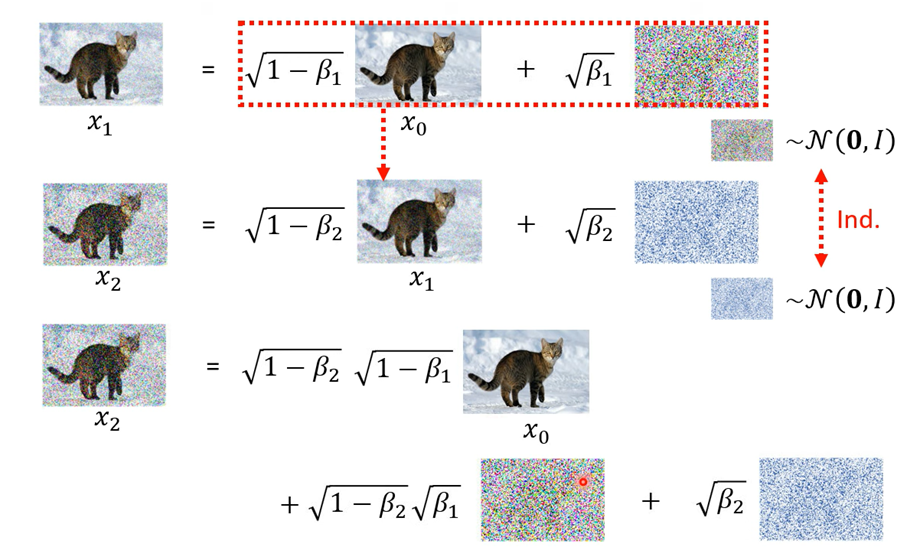
因为不同时间步的高斯分布是独立同分布的，所以可以进行合并。即加噪过程，只需要一步就可以道第 t 步加噪后的𝑥𝑡的概率分布。

则可到q(𝑥𝑡|𝑥0)的条件概率分布：

前向过程的伪代码如下：

逆向过程

        逆向过程是去噪的过程，𝑥𝑇是随机噪声：

逆向过程是一个从𝑝(𝑥𝑇）开始的马尔科夫链，DDPM使用模型𝑝𝜃(𝑥𝑡|𝑥𝑡−1)来拟合逆向过程：

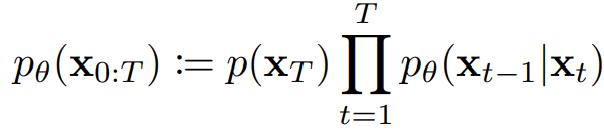
是一个不参与训练的，与时间相关的常数，实验 证明和的结果是类似的。

如果知道𝑝𝜃(𝑥𝑡-1|𝑥𝑡)，就可以从𝑥𝑇开始，逐步还原出图像𝑥0。但是𝑝𝜃(𝑥𝑡-1|𝑥𝑡)无法直接得到，但是可以借助贝叶斯公式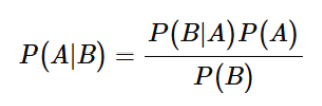得到。

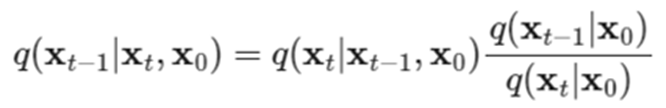
由前向过程的推到可得

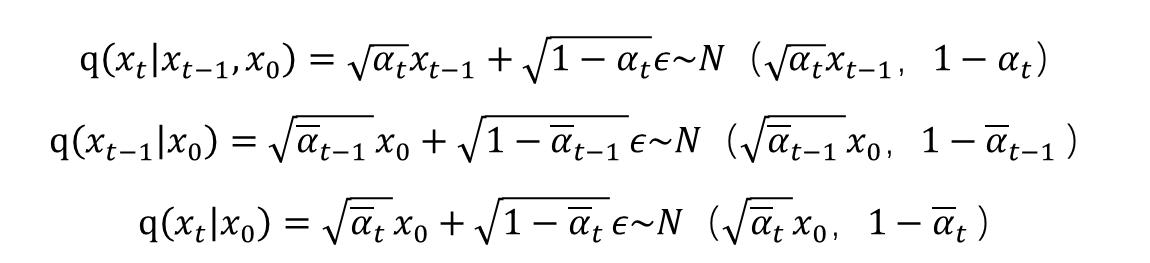
正态分布中的相乘就是指数的相加，相除就是指数的相减，所以可以化简为：

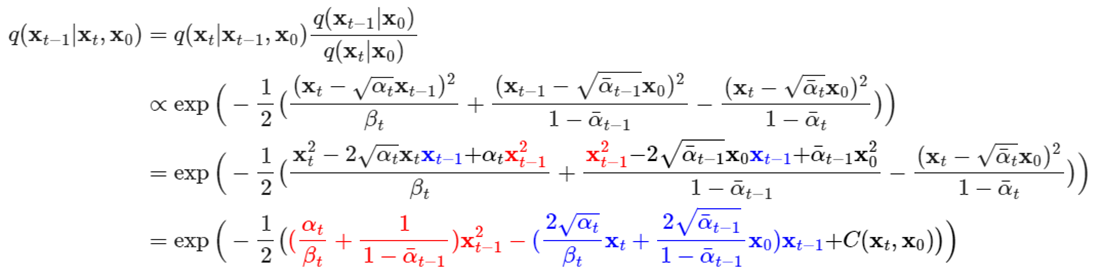
从而，可以得到均值和方差：

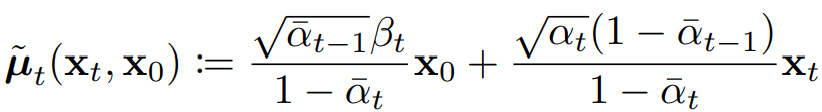
方差是固定值，均值是与𝑥t和𝑥0相关，在反向传播中，𝑥0是未知的，但是利用前向过程的推导公式

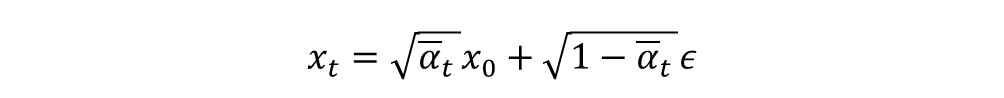
所以均值可以化简为：

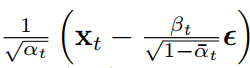
        DDPM是训练一个只和 𝑥t 有关的神经网络 𝜖𝜃(𝑥𝑡，𝑡)来代替 𝜖，那么 q(𝑥𝑡−1|𝑥𝑡,𝑥0) 就会退化为𝑝𝜃(𝑥𝑡-1|𝑥𝑡) 。

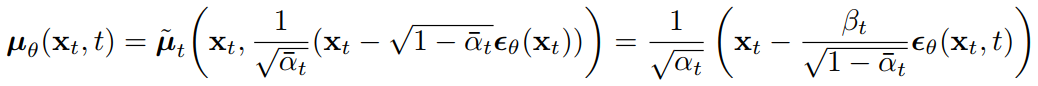
因为αt := 1 - βt，所以：

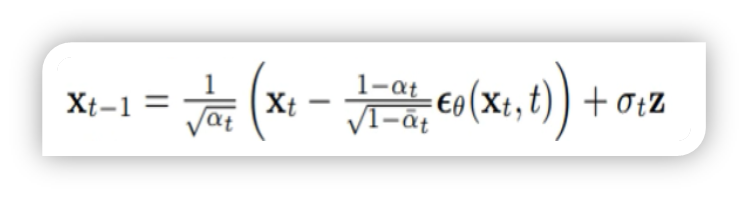
优化目标

        训练是优化负对数似然：

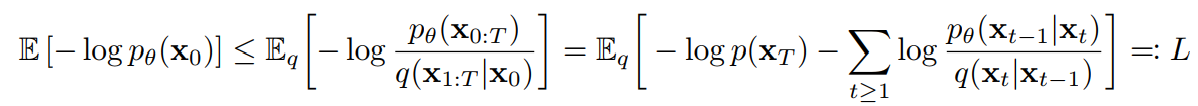
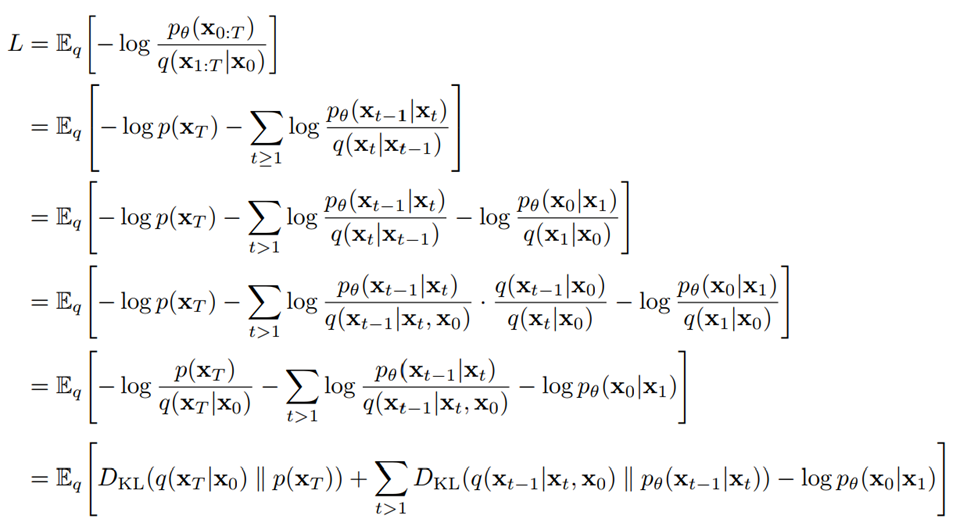
        以下是 L 的另一种形式。虽然难以估计，但对讨论很有用。

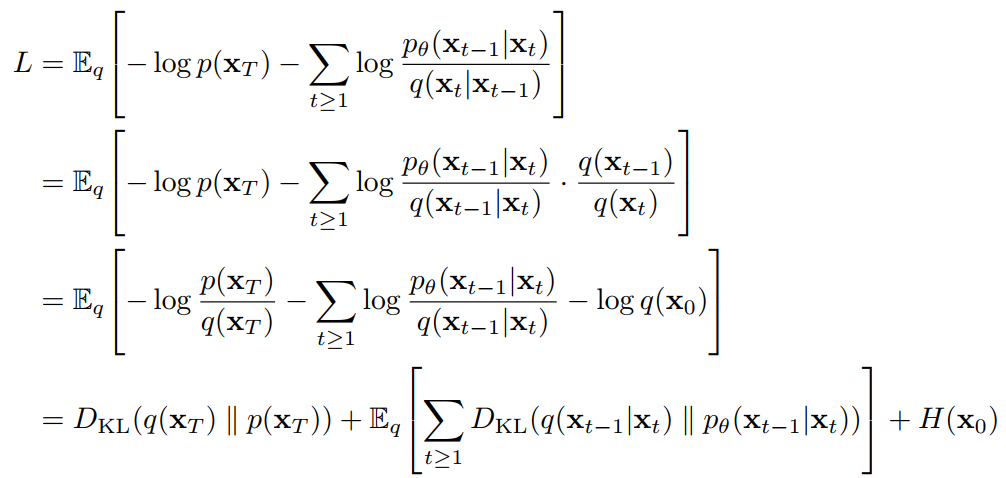
将L重写为：

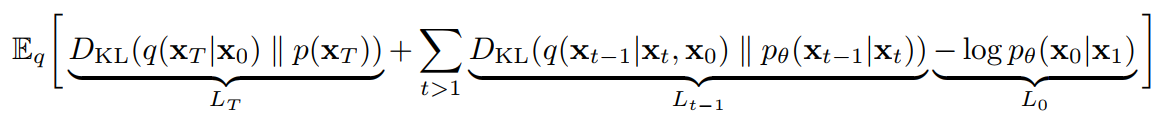
DDIM

       虽然 DDPM 的马尔科夫生成过程可以得到高质量的图像，但因为 DDPM 把采样过程也是一个马尔科夫链，所以需要重新几百上千个步骤才能生成一张图像，耗时很大。DDPM学习目标 只与边缘分布 q(xt|x0) 有关，而不是直接和联合分布 q(x1:T|x0)有关。

       有很多形式的联合分布能够满足 q(xt|x0) ，这样的话，采样过程就不一定需要是马尔科夫链。

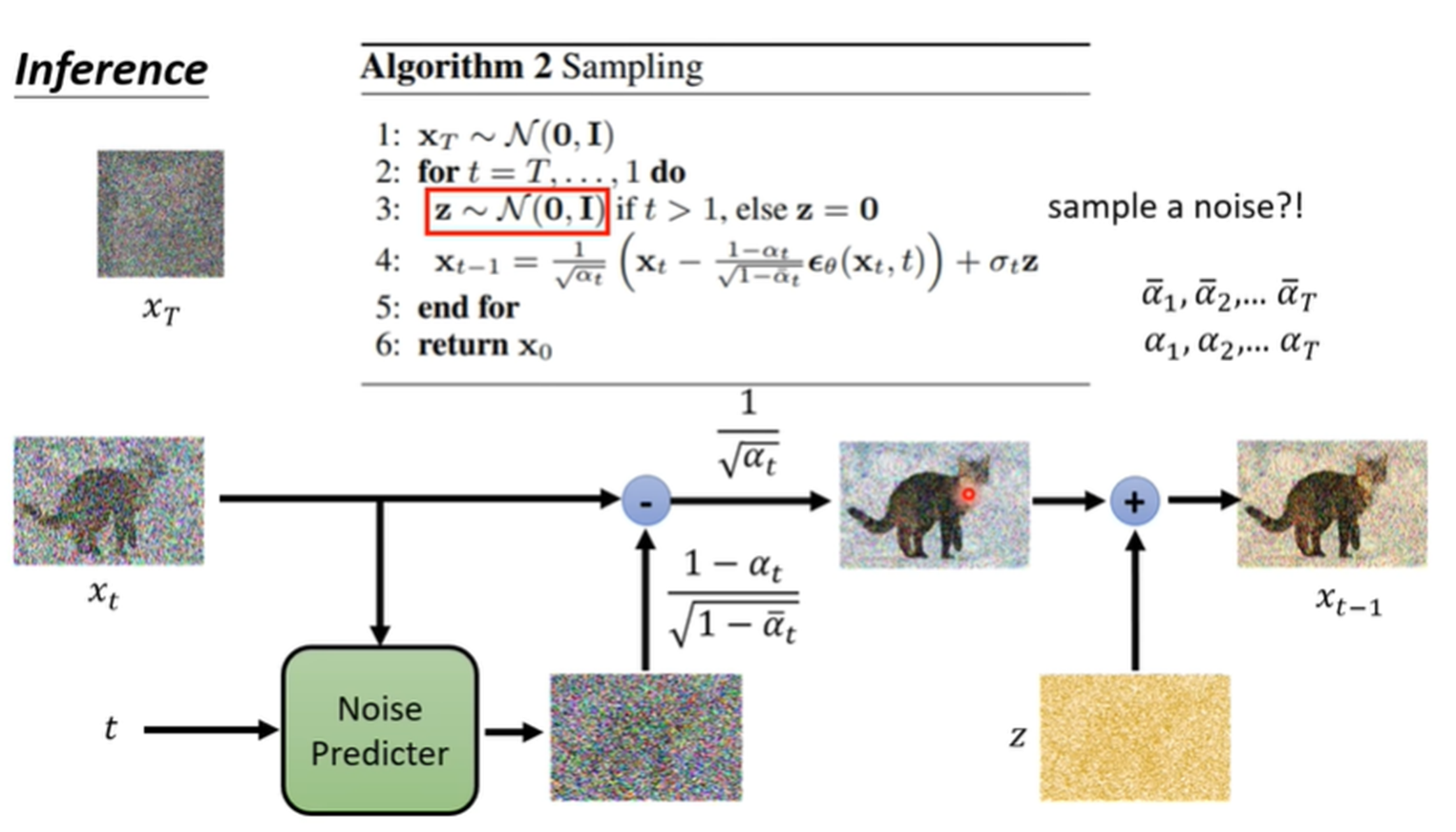
        DDPM中采样过程是一个随机过程，所以需要要加z，如下所以：

        DDIM 优化时与 DDPM 一样，对噪声进行拟合，但 DDIM 提出了通过一个更短的 Forward Processes 过程，通过减少采样的步数，来加快采样速度。 是独立的值，不是由𝛼𝑡连乘得到的。因为此时的 𝛼𝑡没有定义，只是为了和DDPM的符号对应上。同样𝑝𝜃(𝑥𝑡-1|𝑥𝑡)无法直接得到，用𝑝𝜃(𝑥𝑡-1|𝑥𝑡，𝑥0)。

前向过程

        前向过程如下：

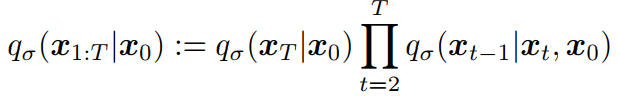
qσ(𝑥𝑇|𝑥0）的概率分布为：

当t>1时，qσ(𝑥𝑡-1|𝑥𝑡,𝑥0)概率分布为：

正向过程可由贝叶斯法则推导得出：

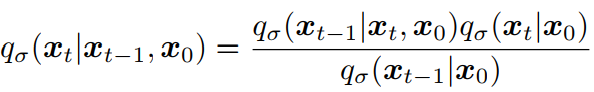
这里的正向过程不再是马尔可夫过程，因为每个 𝑥𝑡 可能同时依赖于 𝑥𝑡-1 和 𝑥0。σ 的大小控制着正向过程的随机程度；当 σ 趋近于 0 时，我们达到一种极端情况，即只要观察到 𝑥0 和某个 t 时刻的𝑥𝑡，那么𝑥𝑡-1 就变得已知且固定。

逆向过程

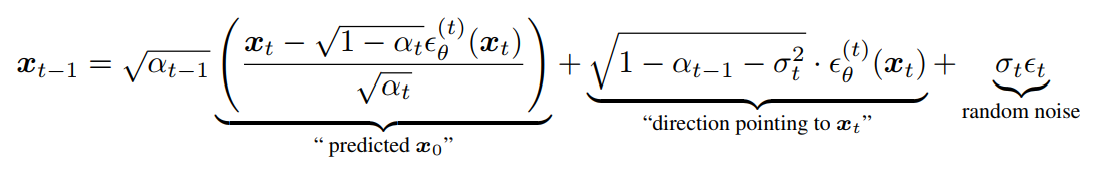
 当时，DDIM就 变成了DDPM。对于所有的t，σt = 0时，在给定𝑥𝑡-1和𝑥0时，前向过程是确定性的，除了t = 1。在生成过程中，随机噪声𝜖t之前的系数变为零。

Flow Matching

定义1：

        凡含有参数，未知函数和未知函数导数 (或微分) 的方程，称为微分方程，有时简称为方程，未知函数是一元函数的微分方程称作常微分方程，未知函数是多元函数的微分方程称作偏微分方程。微分方程中出现的未知函数最高阶导数的阶数，称为微分方程的阶。

训练

        训练的时候，从视频隐空间中得到一个样本X1，从[0, 1]中采样一个time-step t ，采样一个服从 N(0, 1)的噪声，用它们构建一个训练样本Xt。训练模型来预测速度，从Xt变成X1的速度。Flow Matching的重点工作是构建Xt。常采用的是简单的线性插值或the optimal transport path，以OT为例。

其中，σmin = 10-5，可以得到速度的GT

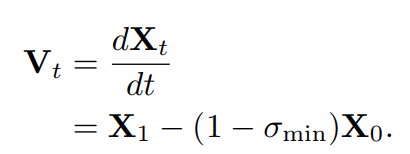
模型参数用θ表示， text prompt embedding用 P表示，预测的速度用u(Xt, P, t)表示。模型的训练目标是最小化GT和预测速度的均方误差。

推理

        推理阶段，首先从N(0, 1)采样得到X0，然后使用一个常微分方程求解器和模型的估计值去计算X1。常用的是一阶欧拉ODE求解器，它为模型提供了特定的的N个时间步的离散集。

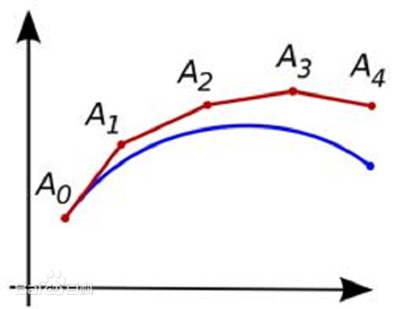
        Xt是一条曲线，Vt是曲线的切线斜率。一阶Euler 方法沿着切线走一小步 (α)，然后在新的位置重新计算斜率，继续前进。虽然简单，但这种“直线逼近”在步长足够小时能很好地追踪曲线。