域名如何做网站大连住建部官网
C++ 红黑树实现详解:理论+代码+图解
文章目录
- C++ 红黑树实现详解:理论+代码+图解
- 一、红黑树的概念
- 1.1 红黑树的规则
- 1.2 红黑树的效率
- 1.3 红黑树和AVL树的比较
- 二、红黑树的实现
- 2.1 红黑树的结构
- 2.2 红黑树的插入
- 2.2.1 插入结点是根结点
- 2.2.2 插入结点的叔叔是红色
- 2.2.3 插入结点的叔叔是黑色
- 2.2.3.1 LL型
- 2.2.3.2 RR型
- 2.2.3.3 RL型
- 2.2.3.4 LR型
- 2.2.4 红黑树的插入代码实现
- 2.3 红黑树的查找
- 2.4 红黑树的验证
- 2.5 红黑树的删除
- 2.5.1 只有左孩子/右孩子:代替后变黑
- 2.5.2 没有孩子
- 2.5.2.1 没有孩子: 删除红节点
- 2.5.2.2 没有孩子: 删除黑节点
- 2.5.2.2.1 没有孩子: 删除黑节点(兄弟是黑色)
- 2.5.2.2.1.1 没有孩子: 删除黑节点(兄弟是黑色)兄弟至少有一个红孩子
- 第一种情况:LL 变色+旋转
- 第二种情况:RR 变色+旋转
- 第三种情况:LR 变色+旋转
- 第四种情况:RL 变色+旋转
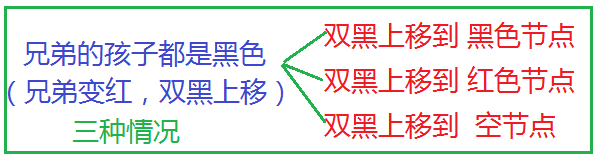
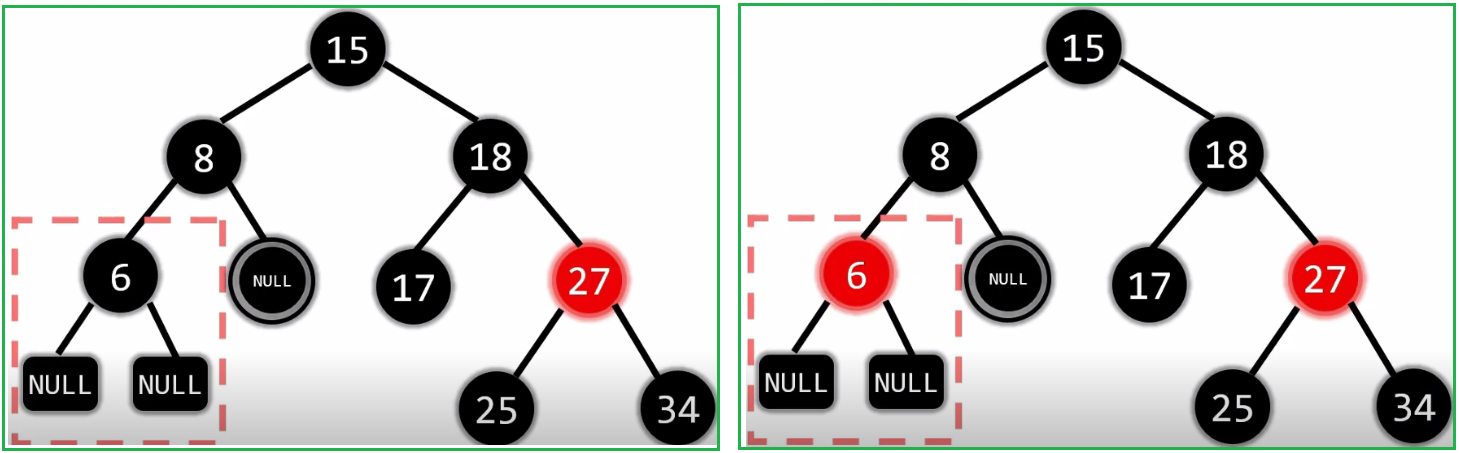
- 2.5.2.2.1.2 没有孩子: 删除黑节点(兄弟是黑色)兄弟的孩子都是黑色
- (1)第一种情况
- (2)第二种情况
- (3)第三种情况
- 2.5.2.2.2 没有孩子: 删除黑节点(兄弟是红色)
- 2.5.3 删除的代码实现
- 三、源代码总结
一、红黑树的概念

1.1 红黑树的规则



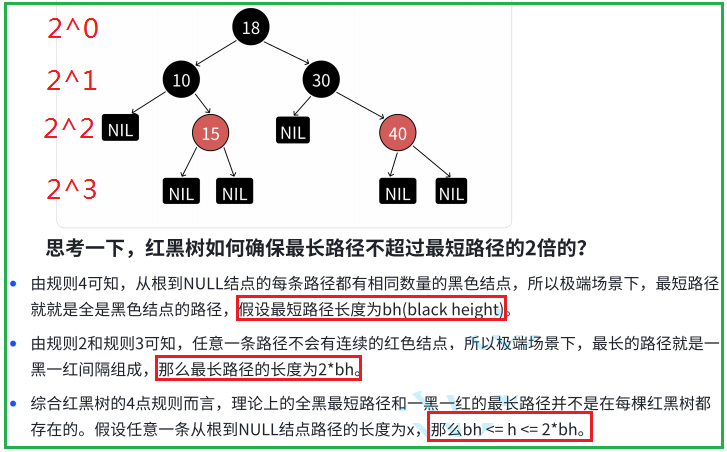 —
—
1.2 红黑树的效率

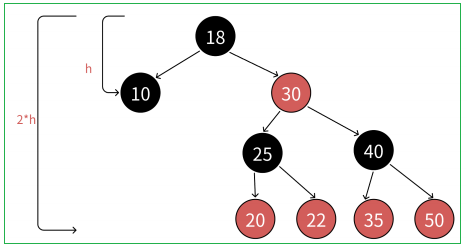
1.3 红黑树和AVL树的比较

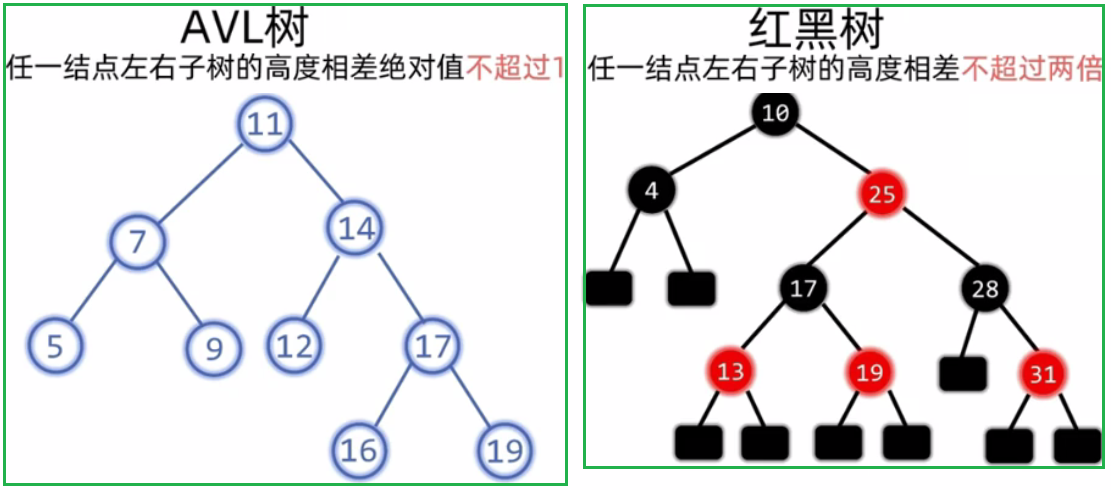
二、红黑树的实现
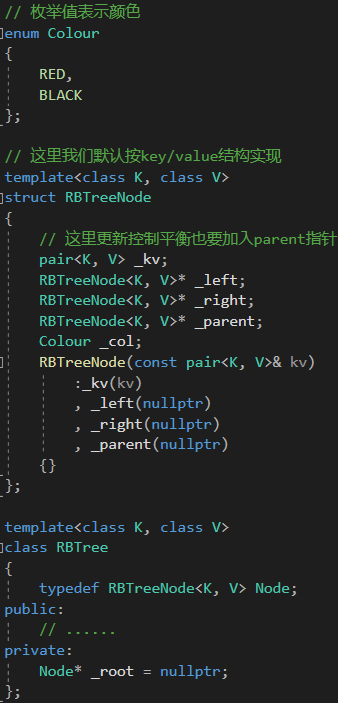
2.1 红黑树的结构
这里用枚举值表示颜色,默认按key/value结构实现,更新控制平衡也要加入parent指针!
2.2 红黑树的插入
红黑树插入节点和二叉搜索树是一样的,但是红黑树有红黑两种颜色标识
红黑树的插入:关键看叔叔uncle

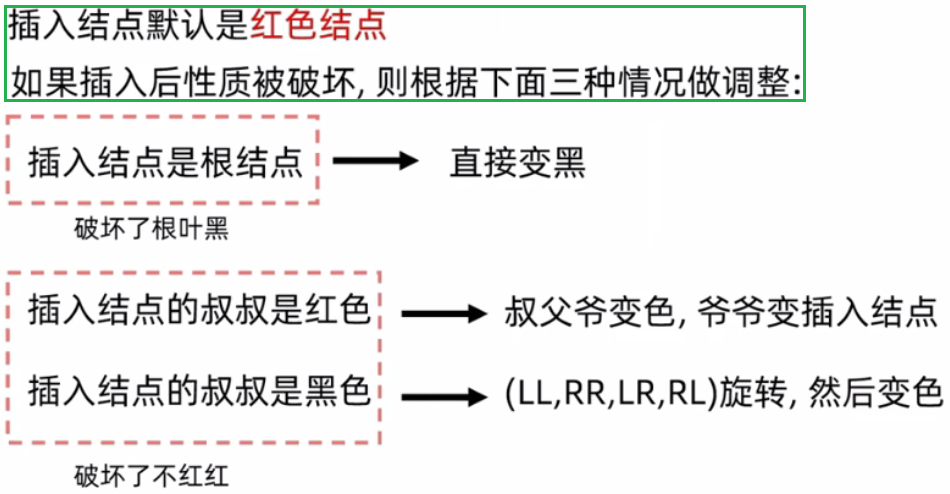
下面介绍如果红黑树的结构被破坏了,需要做的以下三种调整!
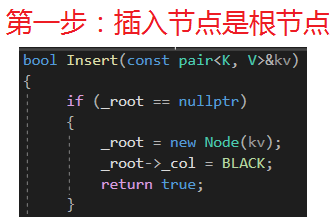
2.2.1 插入结点是根结点
这里会违反根叶黑的性质,直接把根节点变黑即可

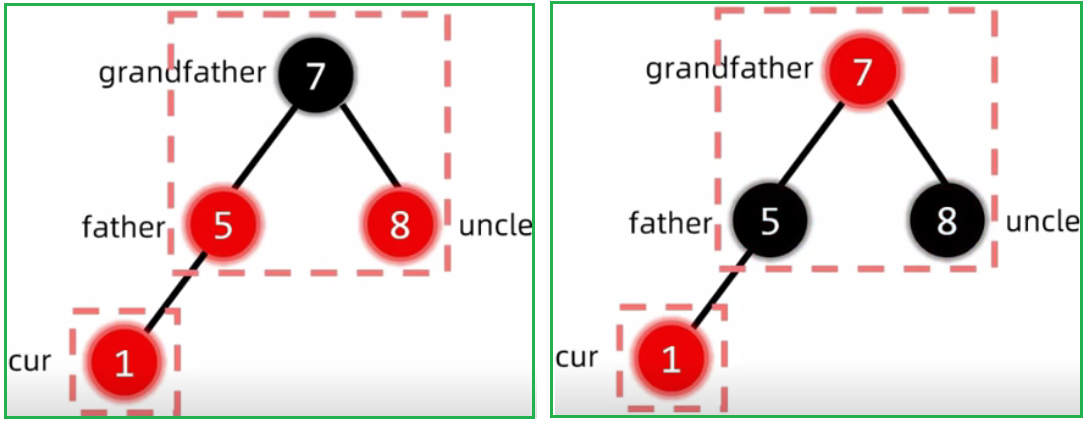
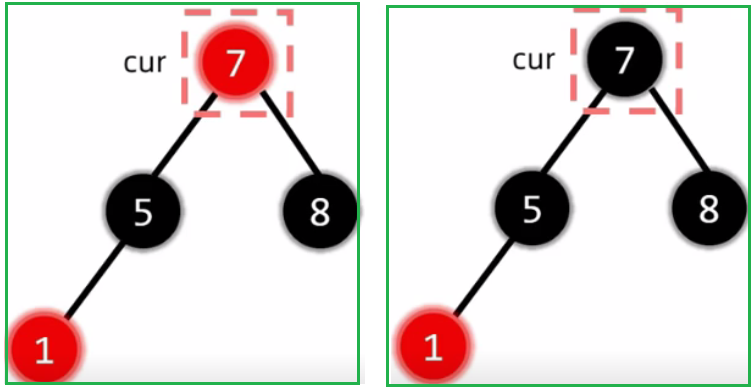
2.2.2 插入结点的叔叔是红色
对cur的父亲、叔叔、爷爷三个节点进行变色(红变黑,黑变红)
随后让爷爷变成cur插入节点:cur指向爷爷,进一步向上判定是否违反红黑树性质
对于插入节点的叔叔是红色,可能不止调整一次,每次调整完,都需要跳转到爷爷那继续判定调整
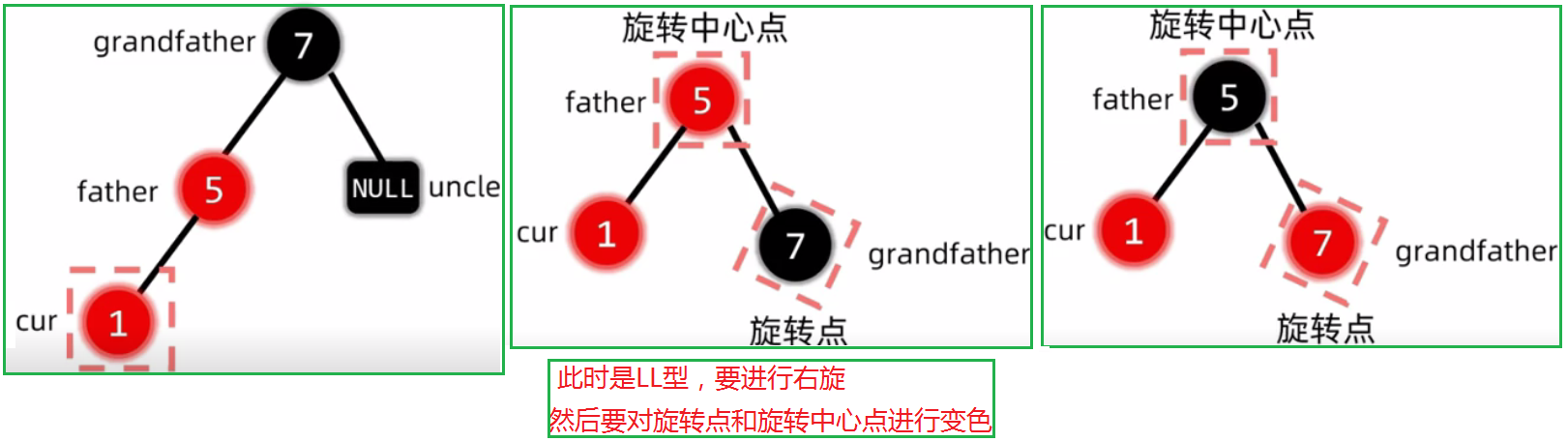
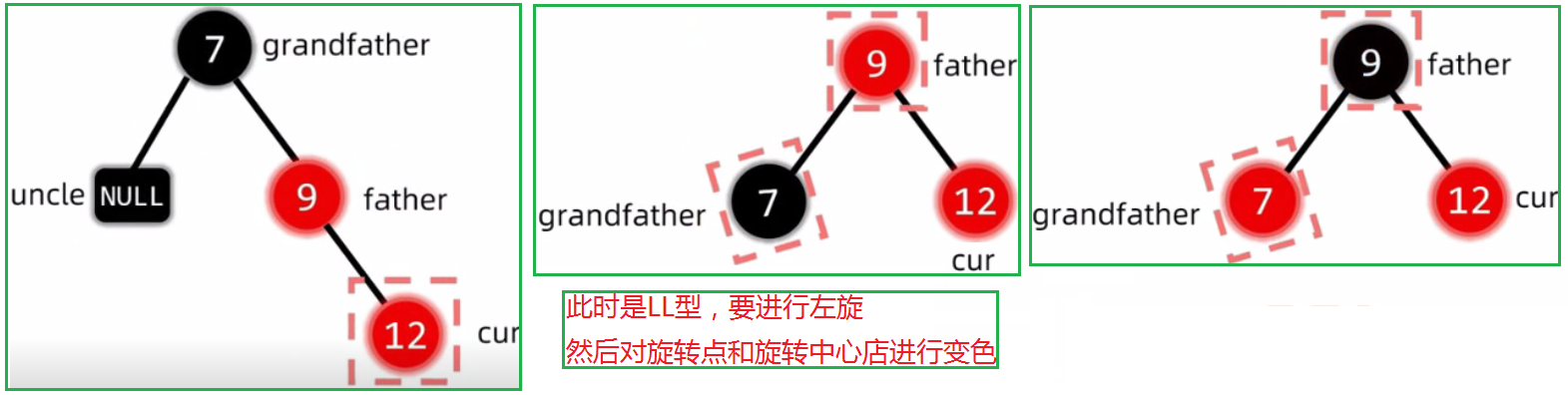
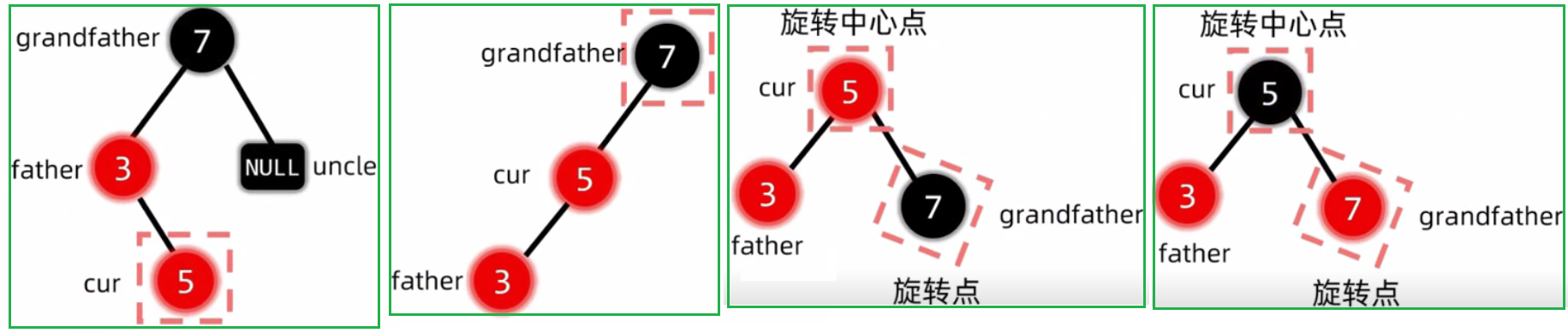
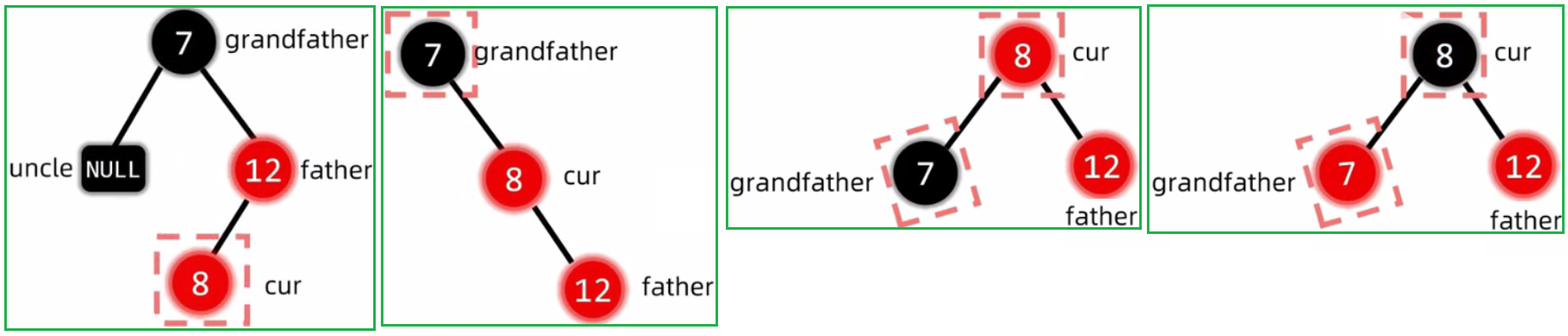
2.2.3 插入结点的叔叔是黑色
插入节点的叔叔是黑色:(LL,RR,LR,RL)旋转,然后变色
2.2.3.1 LL型
2.2.3.2 RR型
2.2.3.3 RL型

2.2.3.4 LR型

2.2.4 红黑树的插入代码实现
旋转代码的实现跟AVL树是一样的,只是不需要更新平衡因子
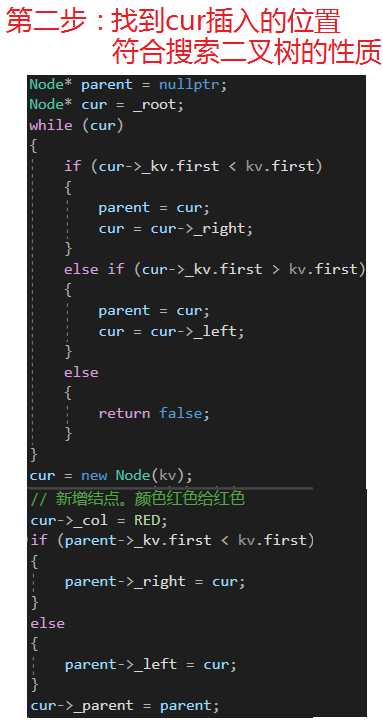



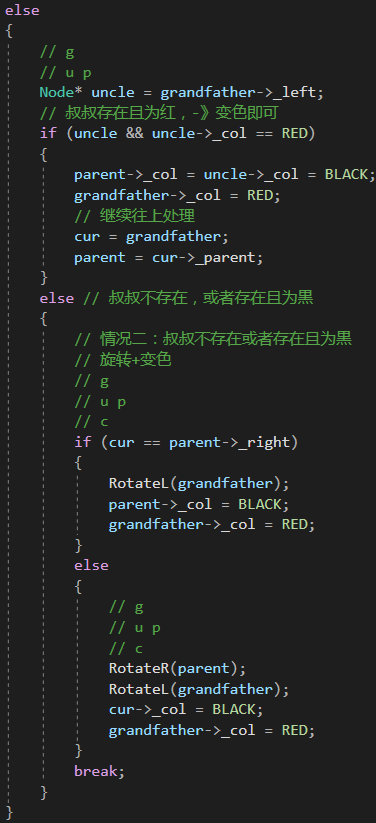
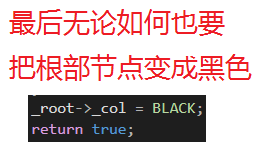
代码如下(示例):
bool Insert(const pair<K, V>&kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);// 新增结点。颜⾊红⾊给红⾊cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;// g// p uif (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// u存在且为红 -》变⾊再继续往上处理parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// u存在且为⿊或不存在 -》旋转+变⾊if (cur == parent->_left){// g// p u//c//单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// c//双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{// g// u pNode* uncle = grandfather->_left;// 叔叔存在且为红,-》变⾊即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为⿊{// 情况⼆:叔叔不存在或者存在且为⿊// 旋转+变⾊// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}
2.3 红黑树的查找
按二叉搜索树逻辑实现即可,搜索效率为O(logN)
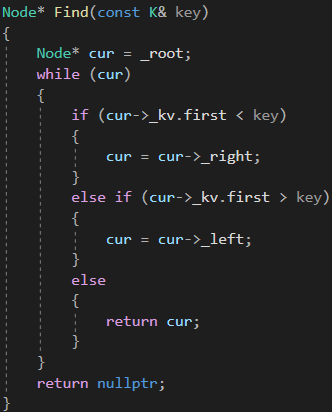
2.4 红黑树的验证

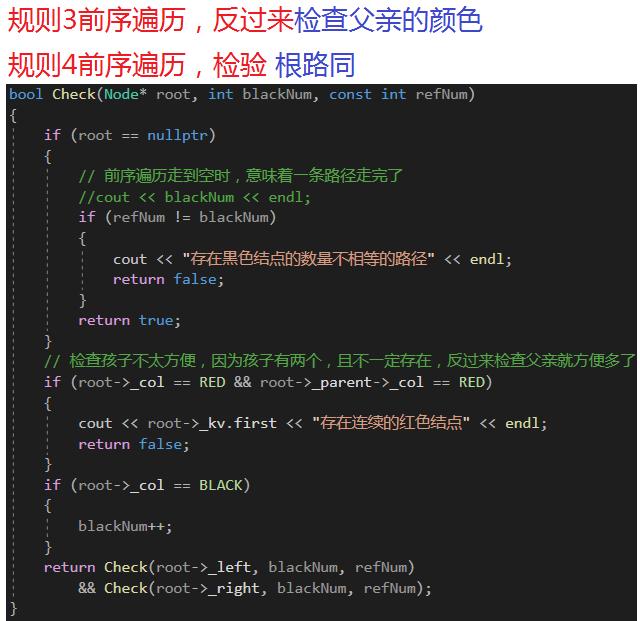
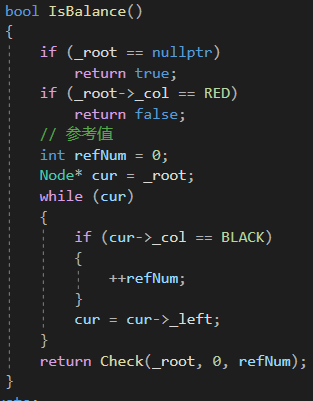
代码如下(示例):
bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍历⾛到空时,意味着⼀条路径⾛完了//cout << blackNum << endl;if (refNum != blackNum){cout << "存在⿊⾊结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲就⽅便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红⾊结点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}
2.5 红黑树的删除
红黑树的删除主要采用了二叉搜索树的方法
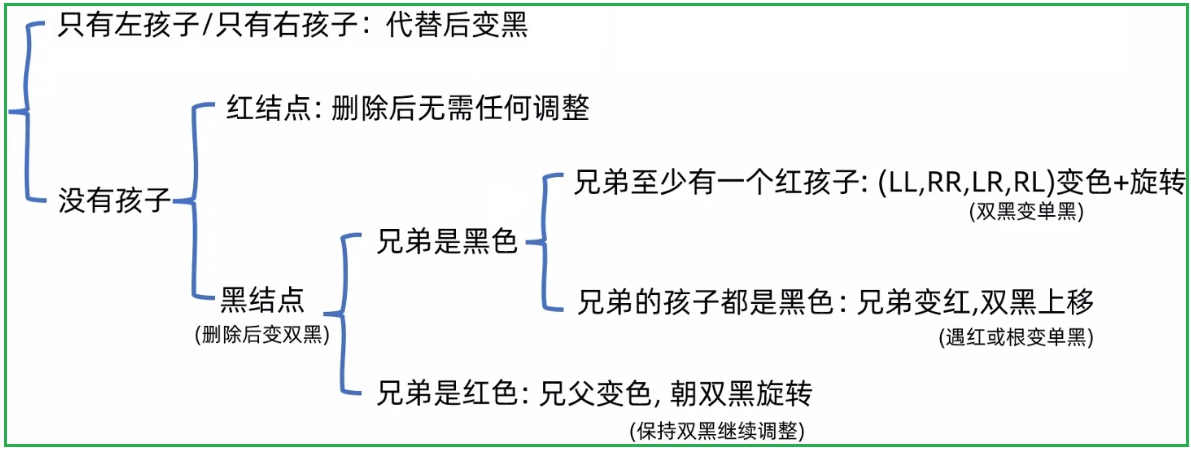
2.5.1 只有左孩子/右孩子:代替后变黑
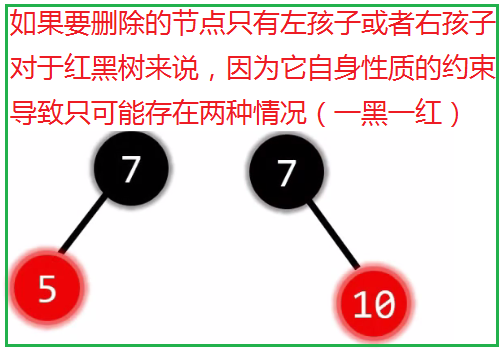
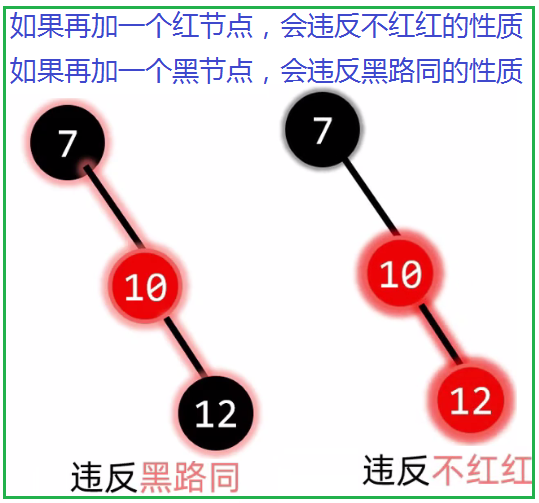


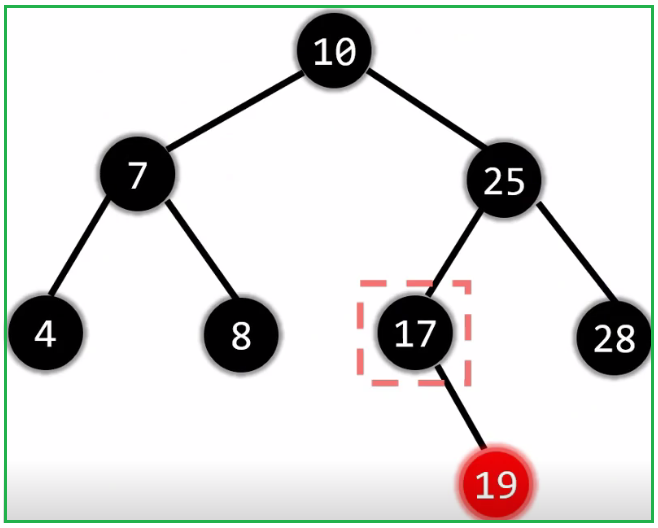
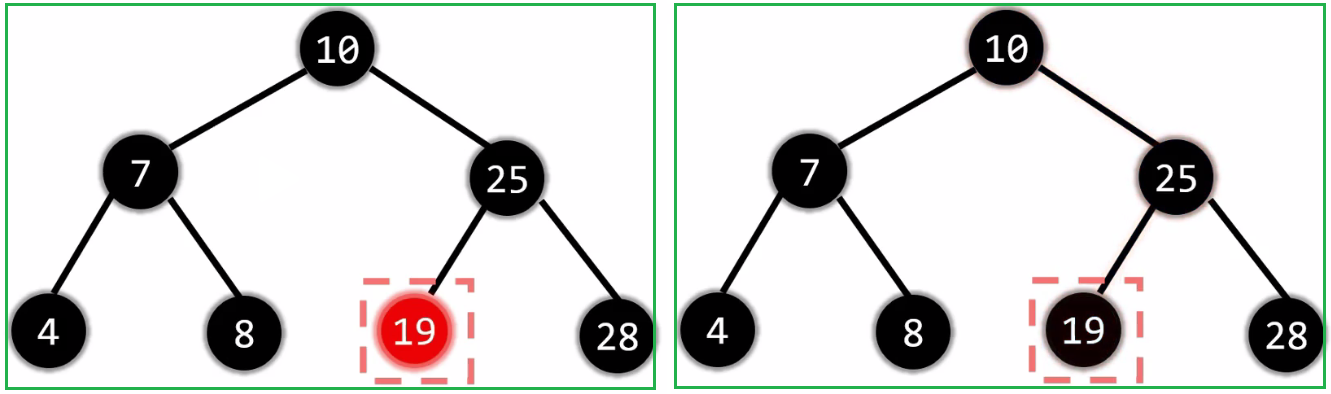
2.5.2 没有孩子
2.5.2.1 没有孩子: 删除红节点
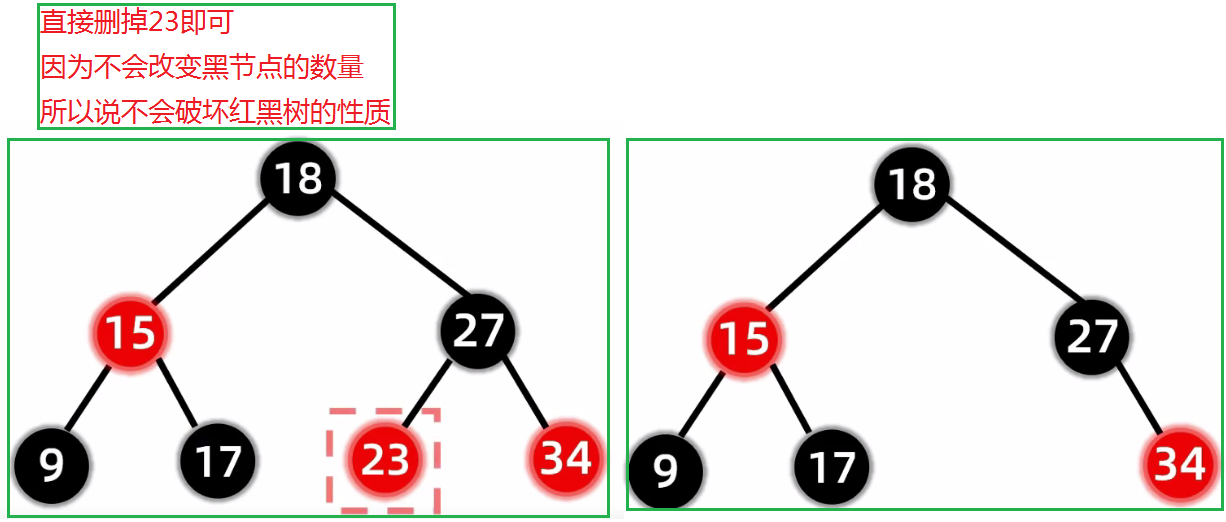
在没有孩子的情况下,如果删除红节点:删除后无需任何调整
2.5.2.2 没有孩子: 删除黑节点
为了更好理解这个过程,我们这里引入了双黑节点的概念
因为删除黑色节点之后,所有经过他的路径都会少一个黑色节点,假设这个节点具有两层黑色
这样我们后面调整的任务就是将这个双黑节点消除或者让他变成单黑节点
2.5.2.2.1 没有孩子: 删除黑节点(兄弟是黑色)
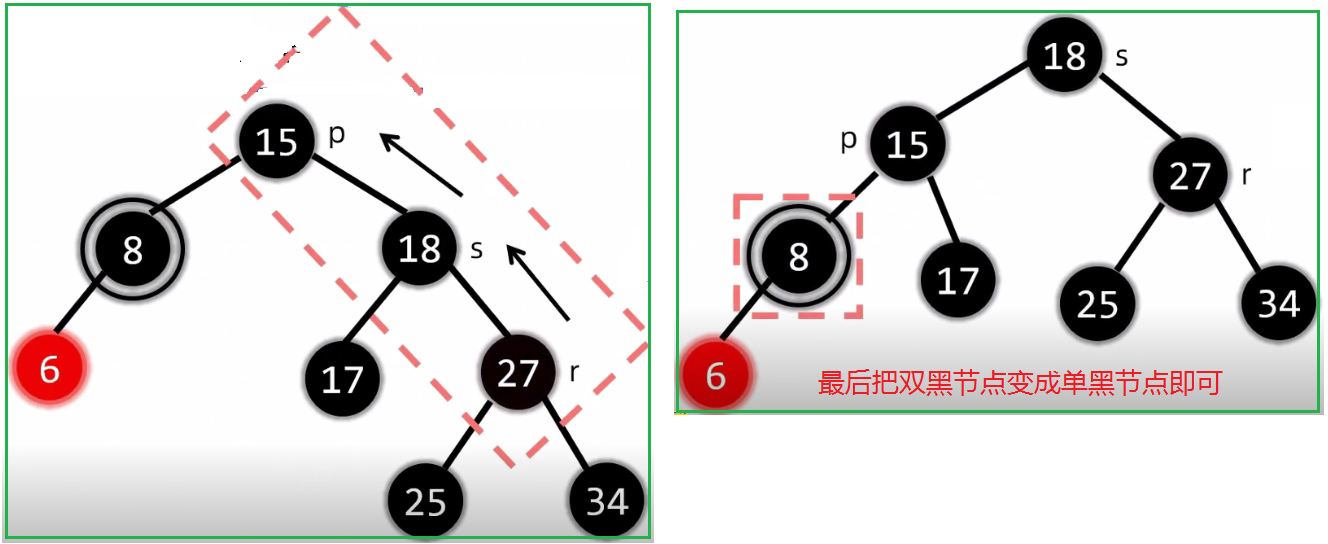
2.5.2.2.1.1 没有孩子: 删除黑节点(兄弟是黑色)兄弟至少有一个红孩子
这里注意:LL和RR是同种类型,LR和RL也是同一种类型
第一种情况:LL 变色+旋转

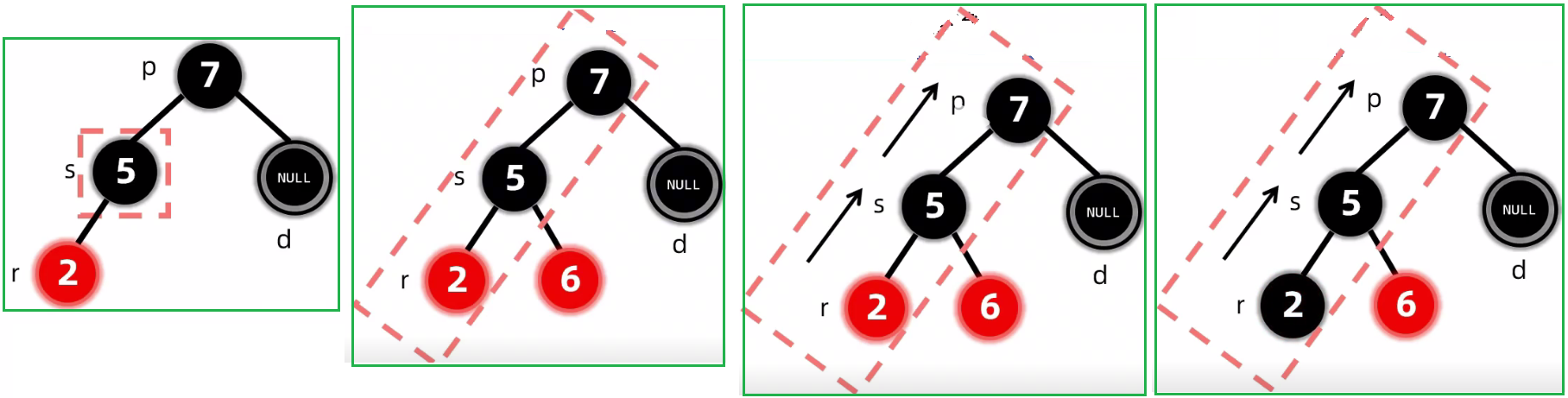
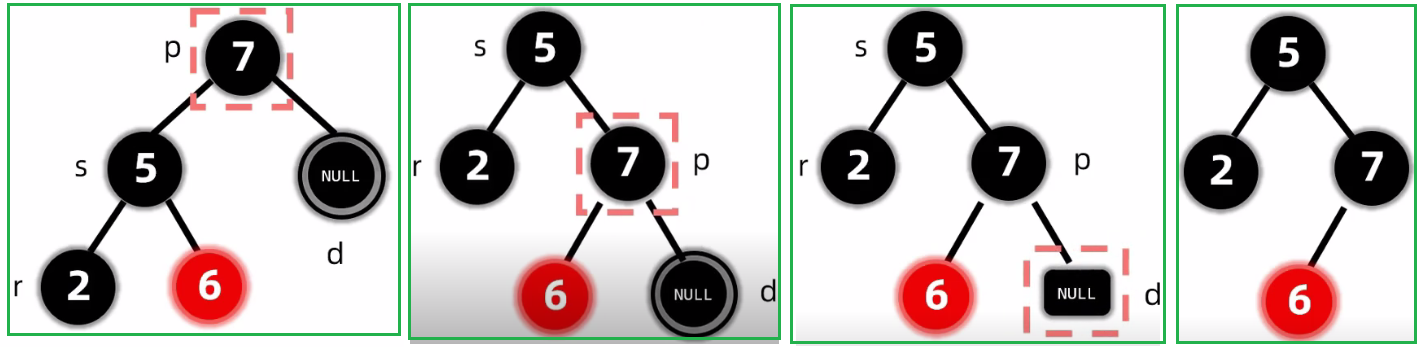
第二种情况:RR 变色+旋转

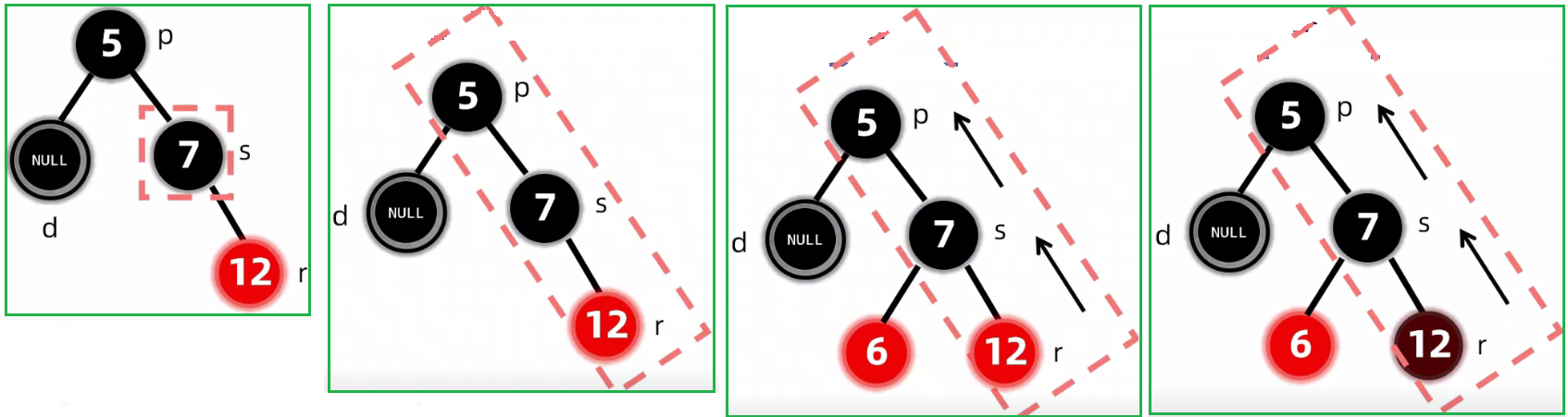
第三种情况:LR 变色+旋转

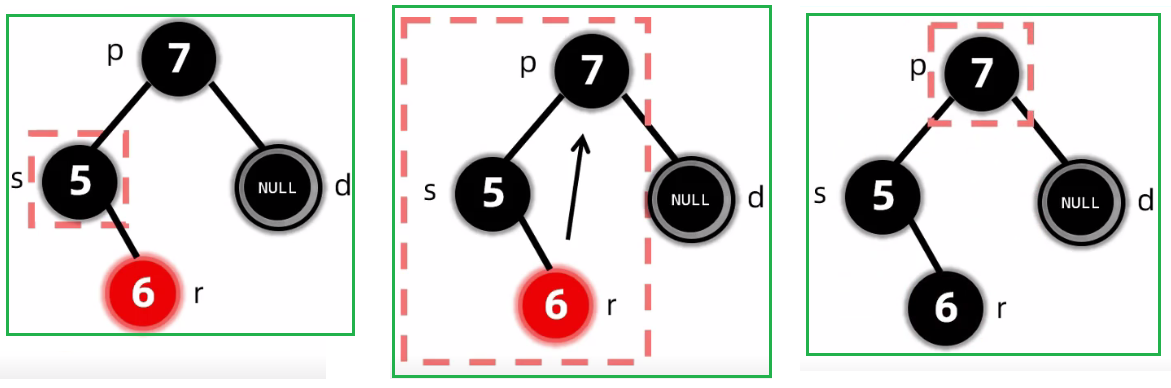
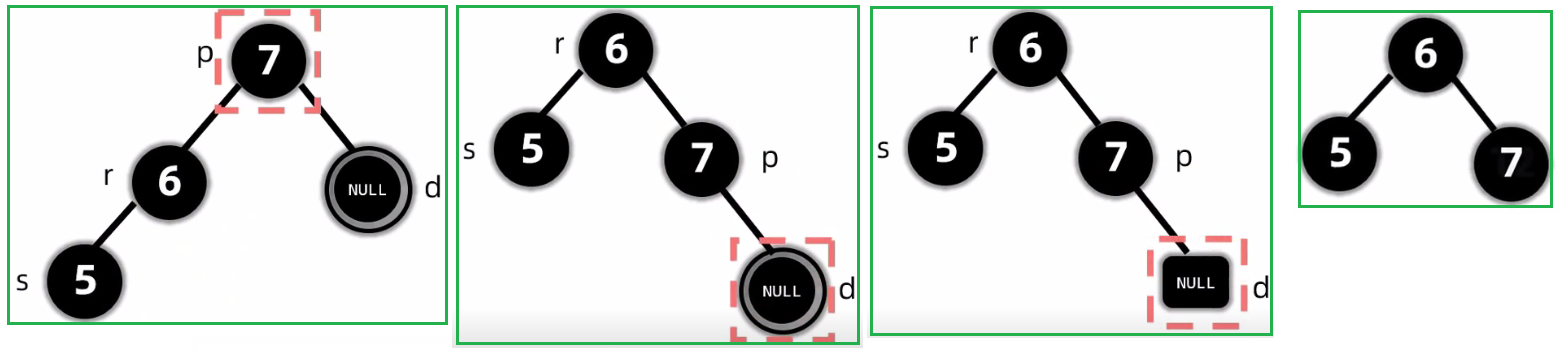
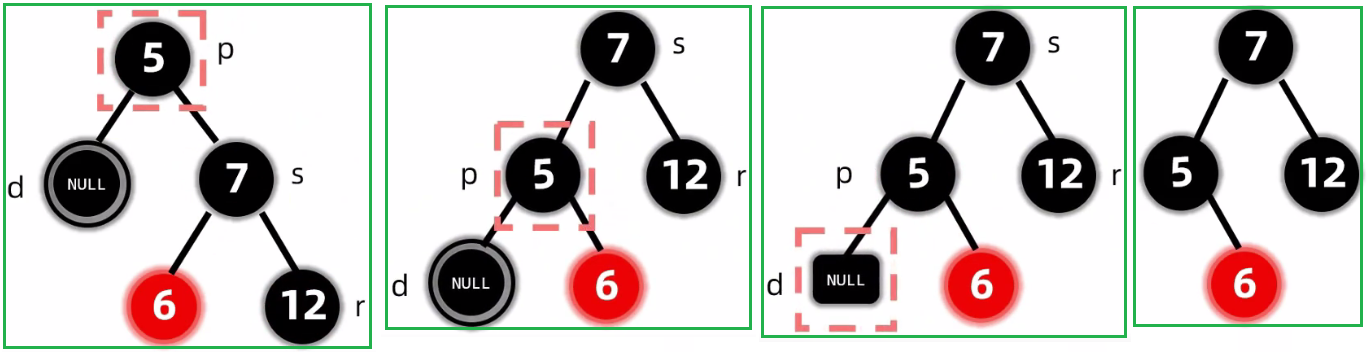
第四种情况:RL 变色+旋转

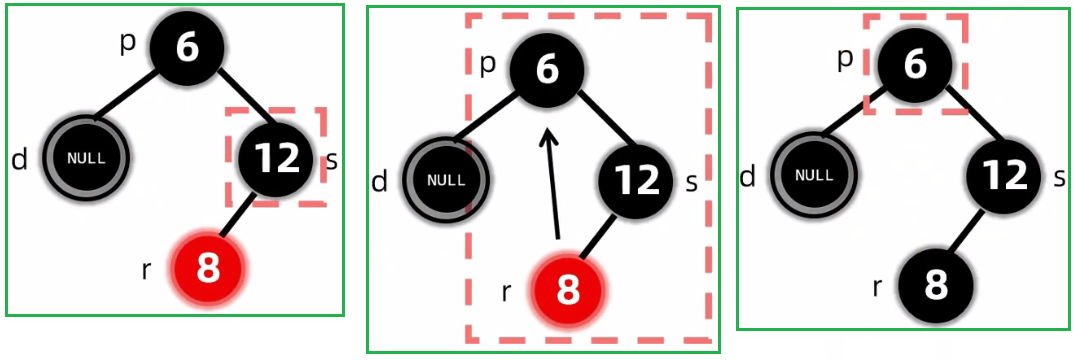
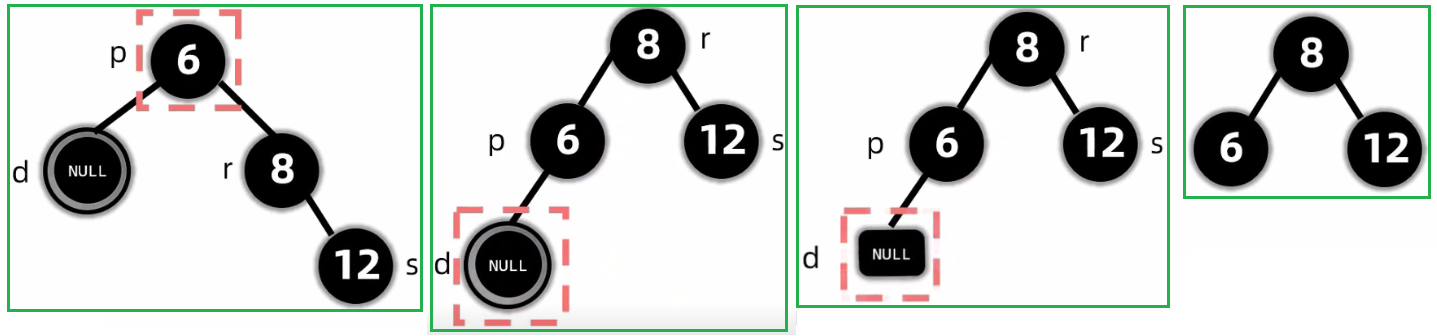
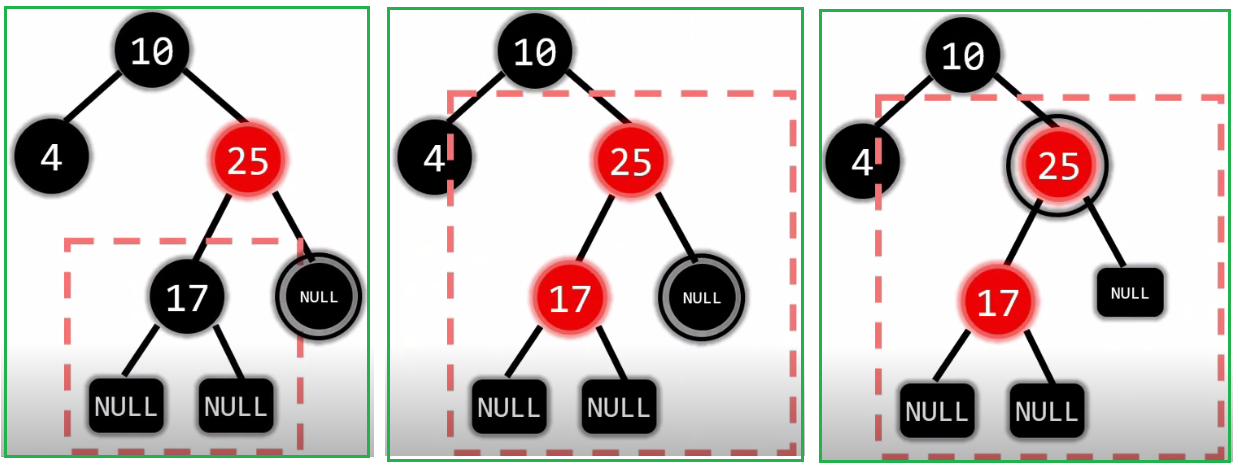
2.5.2.2.1.2 没有孩子: 删除黑节点(兄弟是黑色)兄弟的孩子都是黑色

(1)第一种情况


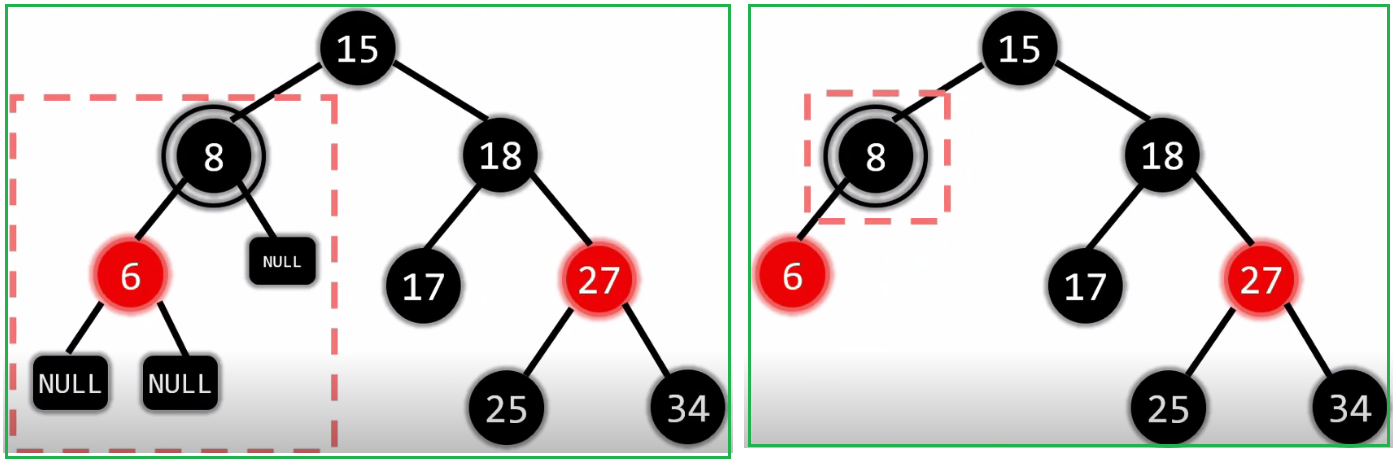


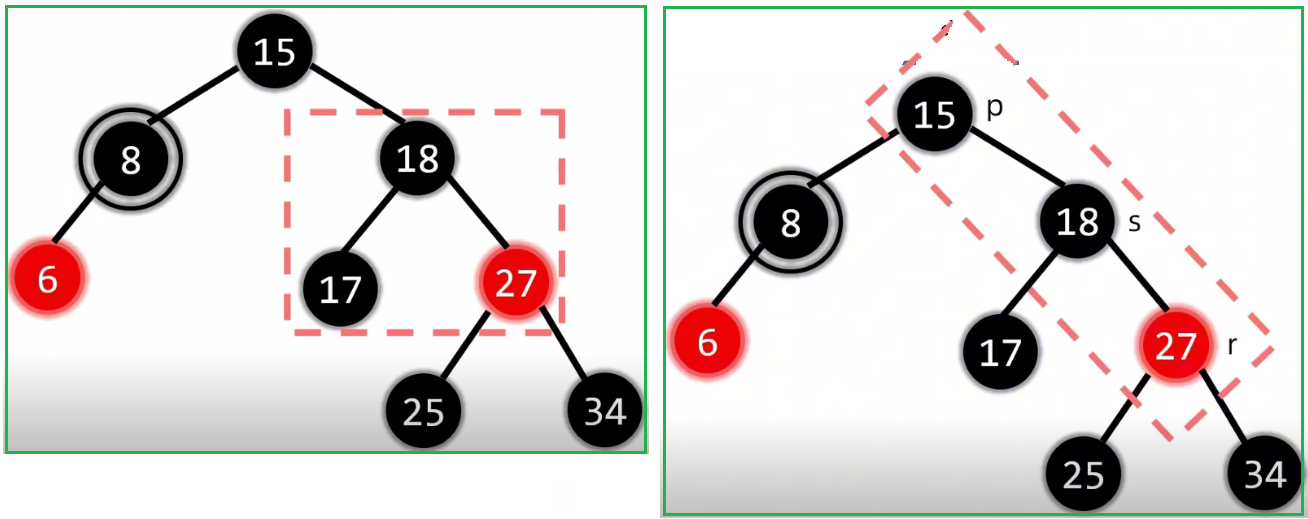
(2)第二种情况

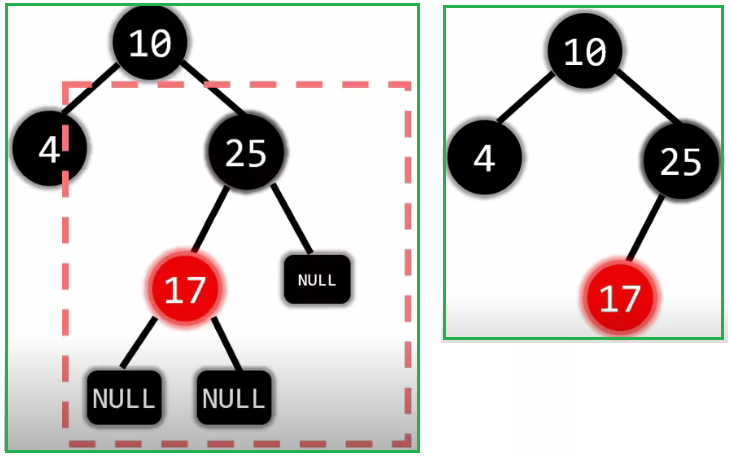
(3)第三种情况

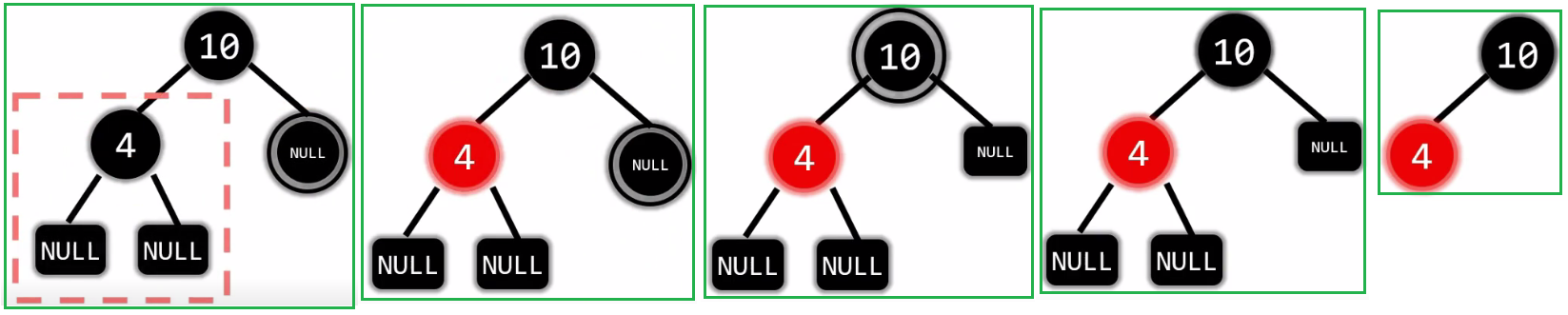
2.5.2.2.2 没有孩子: 删除黑节点(兄弟是红色)


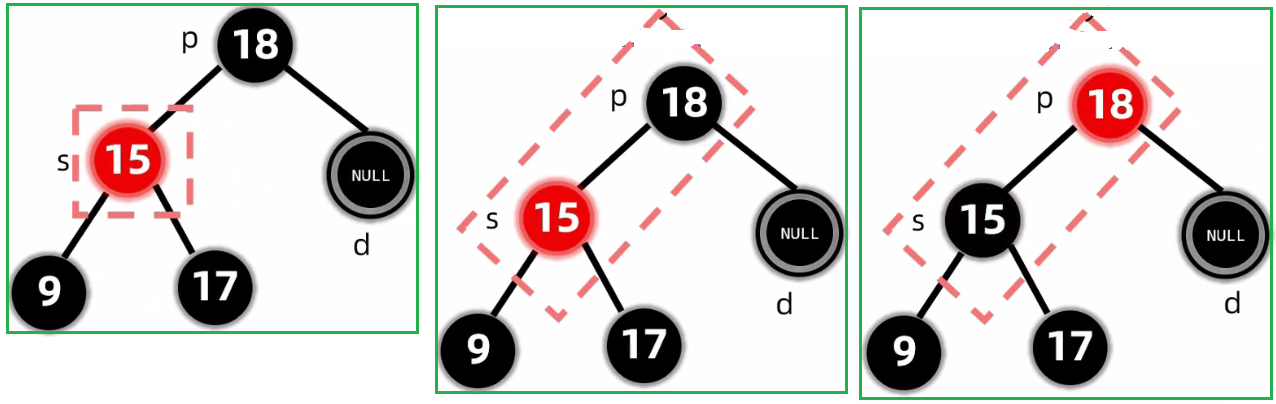

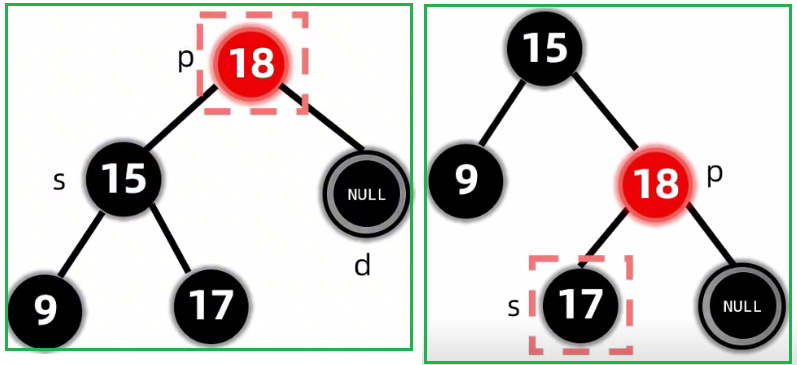

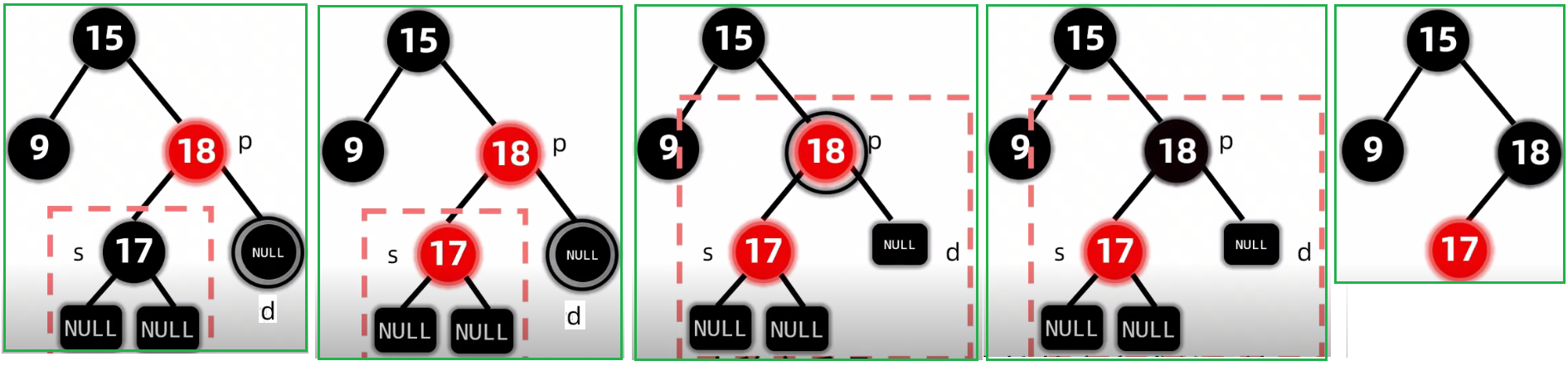
2.5.3 删除的代码实现
代码如下(示例):
//删除函数
bool Erase(const K& key)
{//(一)找到删除节点Node* cur = Find(key);//未找到返回falseif (cur == nullptr){return false;}//记录父节点Node* parent = cur->_parent;//用于标记实际的待删除结点及其父结点Node* delParent = nullptr;Node* delCur = nullptr;if (cur->_left == nullptr) //待删除结点的左子树为空{if (cur == _root) //待删除结点是根结点{_root = _root->_right; //让根结点的右子树作为新的根结点if (_root){_root->_parent = nullptr;_root->_col = BLACK; //根结点为黑色}delete cur; //删除原根结点return true;}else{delParent = parent; //标记实际删除结点的父结点delCur = cur; //标记实际删除的结点}}else if (cur->_right == nullptr) //待删除结点的右子树为空{if (cur == _root) //待删除结点是根结点{_root = _root->_left; //让根结点的左子树作为新的根结点if (_root){_root->_parent = nullptr;_root->_col = BLACK; //根结点为黑色}delete cur; //删除原根结点return true;}else{delParent = parent; //标记实际删除结点的父结点delCur = cur; //标记实际删除的结点}}else //待删除结点的左右子树均不为空{//替换法删除//寻找待删除结点右子树当中key值最小的结点作为实际删除结点Node* minParent = cur;Node* minRight = cur->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_kv = minRight->_kv; //将待删除结点的键值改为minRight的键值delParent = minParent; //标记实际删除的父节点delCur = minRight; //标记实际删除的结点}//记录待删除结点及其父结点,便于后面删除Node* del = delCur;Node* delP = delParent;//(二)调整红黑树AdjustRBTree(delCur, delParent);//(三)进行实际删除DeleteNode(del, delP);return true;
}
void DeleteNode(Node* del, Node* delP)
{if (del->_left == nullptr) //实际删除结点的左子树为空{if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_right;//指向父节点if (del->_right)del->_right->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_right;if (del->_right)del->_right->_parent = delP;}}else //实际删除结点的右子树为空{if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_left;if (del->_left)del->_left->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_left;if (del->_left)del->_left->_parent = delP;}}delete del; //实际删除结点
}
void AdjustRBTree(Node* delCur, Node* delParent)
{if (delCur->_col == BLACK) //删除的是黑色结点{if (delCur->_left) //待删除结点有一个红色的左孩子(不可能是黑色){delCur->_left->_col = BLACK; //将这个红色的左孩子变黑即可}else if (delCur->_right) //待删除结点有一个红色的右孩子(不可能是黑色){delCur->_right->_col = BLACK; //将这个红色的右孩子变黑即可}else //待删除结点的左右均为空{while (delCur != _root) //可能一直调整到根结点{if (delCur == delParent->_left) //待删除结点是其父结点的左孩子{Node* brother = delParent->_right; //兄弟结点是其父结点的右孩子//情况一:brother为红色if (brother->_col == RED){delParent->_col = RED;brother->_col = BLACK;RotateL(delParent);//需要继续处理brother = delParent->_right; //更新brother}//情况二:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delParent->_col == RED){delParent->_col = BLACK;break;}//需要继续处理delCur = delParent;delParent = delCur->_parent;}else{//情况三:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空if ((brother->_right == nullptr) || (brother->_right->_col == BLACK)){brother->_left->_col = BLACK;brother->_col = RED;RotateR(brother);//需要继续处理brother = delParent->_right; //更新brother}//情况四:brother为黑色,且其右孩子是红色结点brother->_col = delParent->_col;delParent->_col = BLACK;brother->_right->_col = BLACK;RotateL(delParent);break; //情况四执行完毕后调整一定结束}}else //delCur == delParent->_right //待删除结点是其父结点的右孩子{Node* brother = delParent->_left; //兄弟结点是其父结点的左孩子//情况一:brother为红色if (brother->_col == RED) //brother为红色{delParent->_col = RED;brother->_col = BLACK;RotateR(delParent);//需要继续处理brother = delParent->_left; //更新brother}//情况二:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delParent->_col == RED){delParent->_col = BLACK;break;}//需要继续处理delCur = delParent;delParent = delCur->_parent;}else{//情况三:brother为黑色,且其右孩子是红色结点,左孩子是黑色结点或为空if ((brother->_left == nullptr) || (brother->_left->_col == BLACK)){brother->_right->_col = BLACK;brother->_col = RED;RotateL(brother);//需要继续处理brother = delParent->_left; //更新brother}//情况四:brother为黑色,且其左孩子是红色结点brother->_col = delParent->_col;delParent->_col = BLACK;brother->_left->_col = BLACK;RotateR(delParent);break; //情况四执行完毕后调整一定结束}}}}}
}三、源代码总结
代码如下(示例):
#include<iostream>
using namespace std;
#include<string>// 枚举值表⽰颜⾊
enum Colour
{RED,BLACK
};// 这⾥我们默认按key/value结构实现
template<class K, class V>
struct RBTreeNode
{// 这⾥更新控制平衡也要加⼊parent指针pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:// ......// 旋转代码的实现跟AVL树是⼀样的,只是不需要更新平衡因⼦bool Insert(const pair<K, V>&kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);// 新增结点。颜⾊红⾊给红⾊cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;// g// p uif (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// u存在且为红 -》变⾊再继续往上处理parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// u存在且为⿊或不存在 -》旋转+变⾊if (cur == parent->_left){// g// p u//c//单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// c//双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{// g// u pNode* uncle = grandfather->_left;// 叔叔存在且为红,-》变⾊即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为⿊{// 情况⼆:叔叔不存在或者存在且为⿊// 旋转+变⾊// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍历⾛到空时,意味着⼀条路径⾛完了//cout << blackNum << endl;if (refNum != blackNum){cout << "存在⿊⾊结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲就⽅便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红⾊结点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}//删除函数bool Erase(const K& key){//(一)找到删除节点Node* cur = Find(key);//未找到返回falseif (cur == nullptr){return false;}//记录父节点Node* parent = cur->_parent;//用于标记实际的待删除结点及其父结点Node* delParent = nullptr;Node* delCur = nullptr;if (cur->_left == nullptr) //待删除结点的左子树为空{if (cur == _root) //待删除结点是根结点{_root = _root->_right; //让根结点的右子树作为新的根结点if (_root){_root->_parent = nullptr;_root->_col = BLACK; //根结点为黑色}delete cur; //删除原根结点return true;}else{delParent = parent; //标记实际删除结点的父结点delCur = cur; //标记实际删除的结点}}else if (cur->_right == nullptr) //待删除结点的右子树为空{if (cur == _root) //待删除结点是根结点{_root = _root->_left; //让根结点的左子树作为新的根结点if (_root){_root->_parent = nullptr;_root->_col = BLACK; //根结点为黑色}delete cur; //删除原根结点return true;}else{delParent = parent; //标记实际删除结点的父结点delCur = cur; //标记实际删除的结点}}else //待删除结点的左右子树均不为空{//替换法删除//寻找待删除结点右子树当中key值最小的结点作为实际删除结点Node* minParent = cur;Node* minRight = cur->_right;while (minRight->_left){minParent = minRight;minRight = minRight->_left;}cur->_kv = minRight->_kv; //将待删除结点的键值改为minRight的键值delParent = minParent; //标记实际删除的父节点delCur = minRight; //标记实际删除的结点}//记录待删除结点及其父结点,便于后面删除Node* del = delCur;Node* delP = delParent;//(二)调整红黑树AdjustRBTree(delCur, delParent);//(三)进行实际删除DeleteNode(del, delP);return true;}void DeleteNode(Node* del, Node* delP){if (del->_left == nullptr) //实际删除结点的左子树为空{if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_right;//指向父节点if (del->_right)del->_right->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_right;if (del->_right)del->_right->_parent = delP;}}else //实际删除结点的右子树为空{if (del == delP->_left) //实际删除结点是其父结点的左孩子{delP->_left = del->_left;if (del->_left)del->_left->_parent = delP;}else //实际删除结点是其父结点的右孩子{delP->_right = del->_left;if (del->_left)del->_left->_parent = delP;}}delete del; //实际删除结点}void AdjustRBTree(Node* delCur, Node* delParent){if (delCur->_col == BLACK) //删除的是黑色结点{if (delCur->_left) //待删除结点有一个红色的左孩子(不可能是黑色){delCur->_left->_col = BLACK; //将这个红色的左孩子变黑即可}else if (delCur->_right) //待删除结点有一个红色的右孩子(不可能是黑色){delCur->_right->_col = BLACK; //将这个红色的右孩子变黑即可}else //待删除结点的左右均为空{while (delCur != _root) //可能一直调整到根结点{if (delCur == delParent->_left) //待删除结点是其父结点的左孩子{Node* brother = delParent->_right; //兄弟结点是其父结点的右孩子//情况一:brother为红色if (brother->_col == RED){delParent->_col = RED;brother->_col = BLACK;RotateL(delParent);//需要继续处理brother = delParent->_right; //更新brother}//情况二:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delParent->_col == RED){delParent->_col = BLACK;break;}//需要继续处理delCur = delParent;delParent = delCur->_parent;}else{//情况三:brother为黑色,且其左孩子是红色结点,右孩子是黑色结点或为空if ((brother->_right == nullptr) || (brother->_right->_col == BLACK)){brother->_left->_col = BLACK;brother->_col = RED;RotateR(brother);//需要继续处理brother = delParent->_right; //更新brother}//情况四:brother为黑色,且其右孩子是红色结点brother->_col = delParent->_col;delParent->_col = BLACK;brother->_right->_col = BLACK;RotateL(delParent);break; //情况四执行完毕后调整一定结束}}else //delCur == delParent->_right //待删除结点是其父结点的右孩子{Node* brother = delParent->_left; //兄弟结点是其父结点的左孩子//情况一:brother为红色if (brother->_col == RED) //brother为红色{delParent->_col = RED;brother->_col = BLACK;RotateR(delParent);//需要继续处理brother = delParent->_left; //更新brother}//情况二:brother为黑色,且其左右孩子都是黑色结点或为空if (((brother->_left == nullptr) || (brother->_left->_col == BLACK))&& ((brother->_right == nullptr) || (brother->_right->_col == BLACK))){brother->_col = RED;if (delParent->_col == RED){delParent->_col = BLACK;break;}//需要继续处理delCur = delParent;delParent = delCur->_parent;}else{//情况三:brother为黑色,且其右孩子是红色结点,左孩子是黑色结点或为空if ((brother->_left == nullptr) || (brother->_left->_col == BLACK)){brother->_right->_col = BLACK;brother->_col = RED;RotateL(brother);//需要继续处理brother = delParent->_left; //更新brother}//情况四:brother为黑色,且其左孩子是红色结点brother->_col = delParent->_col;delParent->_col = BLACK;brother->_left->_col = BLACK;RotateR(delParent);break; //情况四执行完毕后调整一定结束}}}}}}private:Node* _root = nullptr;
};
