C语言应用实例:做不完的畅通工程(并查集)
*并查集(Disjoint Set)
在讲解典例之前,我们先了解一下并查集(Disjoint Set)的概念
什么是并查集?
顾名思义,即检查(查找)+合并
实现方法为:用编号最小的元素标记集合;
定义一个数组set,其中set[i]表示元素i所在集合
举个例子,如下图
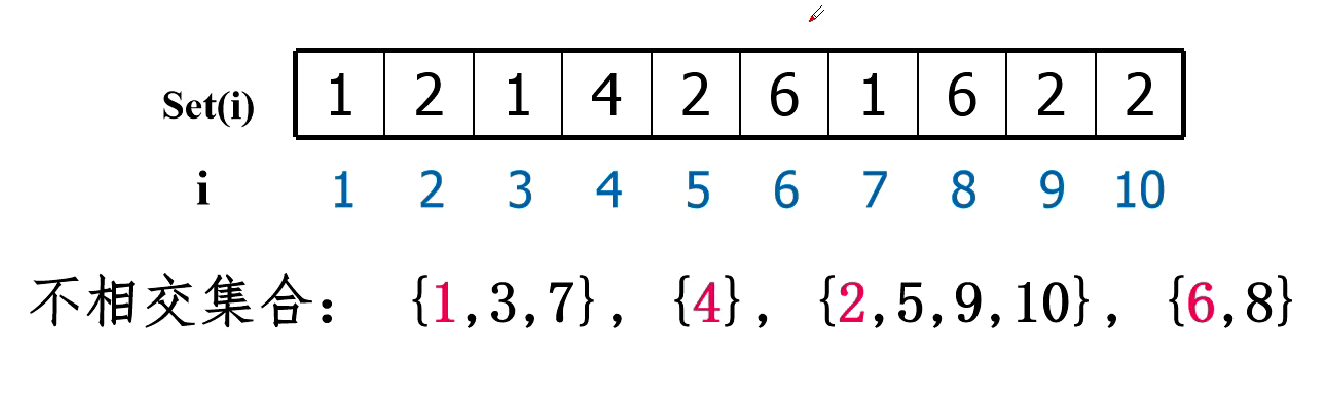
假设一共有十个人(数字表示人名),我们把他们分为四个班级(上图所示的不相交集合),如何让去标记这个班呢?
我们可以选最小的数为班长,用于区分不同班级(集合),每个班的人(即数组下标i)在数组中对应的数就是班长所对应的数,当我们想要合并两个班级时只需把另一个班的人所对应的数更改为两个班长中数较小者所对应的数即可
但是这样做似乎有一个弊端:需要更改的人太多,效率并不高
那么如何去解决这个问题呢?
我们可以采用树状结构
即更改上下级关系(如2班同学班长是2,而2老大是1),这样合并时我们就只需更改另一班班长所对应的数即可

一、畅通工程
1.题目
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
要求:
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是城镇数目N ( < 1000 )和道路数目M;随后的M行对应M条道路,每行给出一对正整数,分别是该条道路直接连通的两个城镇的编号。为简单起见,城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的。
当N为0时,输入结束,该用例不被处理。
对每个测试用例,在1行里输出最少还需要建设的道路数目。
2.题解
这里,我们可以使用并查集(Disjoint Set)
先定义一个find函数用于查找当前元素的根元素(领导)
int find(int x, int arr[]){int r = x;while(arr[r] != r){r = arr[r];}return r;
}然后定义unionSets函数用于合并子集
void unionSets(int a, int b, int arr[]){int rootA = find(a, arr);int rootB = find(b, arr);if(rootA != rootB){if(rootA < rootB){arr[rootB] = rootA;} else {arr[rootA] = rootB;}}
}处理代码如下
int num = 0;int root1 = find(1, arr);for(int j = 2; j <= N; j++){ if(find(j, arr) != root1){num++;arr[find(j, arr)]=root1;}}3.完整代码
#include<stdio.h>
#include<math.h>int find(int x, int arr[]){int r = x;while(arr[r] != r){r = arr[r];}return r;
}void unionSets(int a, int b, int arr[]){int rootA = find(a, arr);int rootB = find(b, arr);if(rootA != rootB){if(rootA < rootB){arr[rootB] = rootA;} else {arr[rootA] = rootB;}}
}int main(){while(1){int N, M;scanf("%d %d", &N, &M);if(N == 0){break;}int arr[N+1]; for(int i = 1; i <= N; i++){arr[i] = i;}for(int i = 0; i < M; i++){int a, b;scanf("%d %d", &a, &b);unionSets(a, b, arr);}int num = 0;int root1 = find(1, arr);for(int j = 2; j <= N; j++){ if(find(j, arr) != root1){num++;arr[find(j, arr)]=root1;}}printf("%d\n", num);}return 0;
}二、畅通工程进阶版
1.题目
某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度
要求:测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目 N(<100) ;随后的 N(N−1)/2 行对应村庄间的距离,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间的距离。为简单起见,村庄从 1 到 N 编号。
当 N 为 0 时,输入结束,该用例不被处理
对每个测试用例,在 1 行里输出最小的公路总长度
2.题解
这题要求的是修路的最优问题
先定义路Road结构体
struct Road{int a, b;//村庄一和村庄二int s;//距离
};然后定义查找和合并函数
int find(int x){if(parent[x] != x){parent[x] = find(parent[x]); }return parent[x];
}void unionSets(int a, int b){int rootA = find(a);int rootB = find(b);if(rootA != rootB){parent[rootB] = rootA;}
}输入步骤略
接下来是核心算法(Kruskal算法)
// Kruskal算法for(int i = 0; i < M && edges < N - 1; i++){int a = rolist[i].a;int b = rolist[i].b;if(find(a) != find(b)){unionSets(a, b);sum += rolist[i].s;edges++;}}3.完整代码
#include<stdio.h>
#include<stdlib.h>struct Road{int a, b;int s;
};int parent[101]; // 并查集数组,大小按最大村庄数设置// 查找根节点
int find(int x){if(parent[x] != x){parent[x] = find(parent[x]); // 路径压缩}return parent[x];
}// 合并集合
void unionSets(int a, int b){int rootA = find(a);int rootB = find(b);if(rootA != rootB){parent[rootB] = rootA;}
}// 比较函数:按距离升序排序
int compare(const void *a, const void *b){struct Road *ro1 = (struct Road*)a;struct Road *ro2 = (struct Road*)b;return ro1->s - ro2->s;
}int main(){int N;while(scanf("%d", &N) && N != 0){int M = N * (N - 1) / 2;struct Road *rolist = (struct Road*)malloc(sizeof(struct Road) * M);// 读取所有道路for(int i = 0; i < M; i++){scanf("%d %d %d", &rolist[i].a, &rolist[i].b, &rolist[i].s);}// 初始化并查集for(int i = 1; i <= N; i++){parent[i] = i;}// 按距离排序qsort(rolist, M, sizeof(struct Road), compare);int sum = 0;int edges = 0; // 已选择的边数// Kruskal算法for(int i = 0; i < M && edges < N - 1; i++){int a = rolist[i].a;int b = rolist[i].b;// 如果两个村庄不在同一集合中,则选择这条边if(find(a) != find(b)){unionSets(a, b);sum += rolist[i].s;edges++;}}printf("%d\n", sum);free(rolist);}return 0;
}三、畅通工程进阶版的进阶版
1.题目
省政府 “畅通工程” 的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可)。
经过调查评估,得到的统计表中列出了有可能建设公路的若干条道路的成本。
现请你编写程序,计算出全省畅通需要的最低成本。
要求:测试输入包含若干测试用例。
每个测试用例的第 1 行给出评估的道路条数 N、村庄数目M(<100) ;随后的 N 行对应村庄间道路的成本,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间道路的成本(也是正整数)。
为简单起见,村庄从 1 到 M 编号。
当 N 为 0 时,全部输入结束,相应的结果不要输出
对每个测试用例,在 1 行里输出全省畅通需要的最低成本。
若统计数据不足以保证畅通,则输出“?”
2.题解
这道题糅合了前两道题所考察的知识点
大概思路没什么变化
主要区别为:多了个检查步骤(如下)
if(connected && edge == M-1){printf("%d\n",sum);} else {printf("?\n");}3.完整代码
#include<stdio.h>
#include<stdlib.h>
#include<math.h>struct Vil{int a,b;int mon;
};int compare(const void *a,const void *b){struct Vil *m1=(struct Vil*)a;struct Vil *m2=(struct Vil*)b;return m1->mon-m2->mon;}int arr[101];find(int x){int r=x;while(arr[r]!=r){r=arr[r];}return r;
}void merge(int a,int b){int roota=find(a);int rootb=find(b);arr[rootb]=roota;
}int main(){while(1){int N,M;scanf("%d %d",&N,&M);if(N==0){break;}struct Vil *vilist=(struct Vil*)malloc(sizeof(struct Vil)*N);for(int i=0;i<N;i++){struct Vil vi;scanf("%d %d %d",&vi.a,&vi.b,&vi.mon);vilist[i]=vi;}for(int i=1;i<=M;i++){arr[i]=i;}if(N<M-1){printf("?\n");continue;}else{qsort(vilist,N,sizeof(struct Vil),compare);int edge=0;int sum=0;for(int i=0;i<N&&edge<M-1;i++){int a=vilist[i].a;int b=vilist[i].b;if(find(a)!=find(b)){merge(a,b);edge++;sum+=vilist[i].mon;}}int root = find(1);int connected = 1;for(int i=2;i<=M;i++){if(find(i) != root){connected = 0;break;}}if(connected && edge == M-1){printf("%d\n",sum);} else {printf("?\n");}}free(vilist);}return 0;
}四、畅通工程进阶版的进阶版的进阶版
1.题目
省政府 “畅通工程” 的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可)。
现得到城镇道路统计表,表中列出了任意两城镇间修建道路的费用,以及该道路是否已经修通的状态。
现请你编写程序,计算出全省畅通需要的最低成本
要求:
测试输入包含若干测试用例。每个测试用例的第 1 行给出村庄数目 N(1<N<100);随后的 N(N−1)/2 行对应村庄间道路的成本及修建状态,每行给 4 个正整数,分别是两个村庄的编号(从 1 编号到 N ),此两村庄间道路的成本,以及修建状态:1 表示已建,0 表示未建。
当 N 为 0 时输入结束
每个测试用例的输出占一行,输出全省畅通需要的最低成本
2.题解
这道题综合了上述三道题所考察的知识点
唯一不同点在于:不需要存储已建的公路相关的村庄数据
for(int i=0;i<M;i++){struct Vil vi;scanf("%d %d %d %d",&vi.a,&vi.b,&vi.mon,&vi.num);if(vi.num==1){merge(vi.a,vi.b);}//只存没修的if(vi.num==0){vilist[k]=vi;k++;}}其他不变
3.完整代码
#include<stdio.h>
#include<stdlib.h>
#include<math.h>struct Vil{int a,b;int mon;int num;
};int compare(const void *a,const void *b){struct Vil *m1=(struct Vil*)a;struct Vil *m2=(struct Vil*)b;return m1->mon-m2->mon;}int arr[101];find(int x){int r=x;while(arr[r]!=r){r=arr[r];}return r;
}void merge(int a,int b){int roota=find(a);int rootb=find(b);arr[rootb]=roota;
}int main(){while(1){int N;scanf("%d",&N);//printf("**%d**",N);if(N==0){break;}int M=N*(N-1)/2;struct Vil *vilist=(struct Vil*)malloc(sizeof(struct Vil)*M);for(int i=1;i<=N;i++){arr[i]=i;}int k=0;for(int i=0;i<M;i++){struct Vil vi;scanf("%d %d %d %d",&vi.a,&vi.b,&vi.mon,&vi.num);if(vi.num==1){merge(vi.a,vi.b);}//只存没修的if(vi.num==0){vilist[k]=vi;k++;}}qsort(vilist,M,sizeof(struct Vil),compare);int edge=M-k;int sum=0;for(int i=0;i<k&&edge<N-1;i++){int a=vilist[i].a;int b=vilist[i].b;if(find(a)!=find(b)){merge(a,b);edge++;sum+=vilist[i].mon;}} printf("%d\n",sum);free(vilist);//printf("------------------------------\n");}return 0;
}