堆相关算法题基础-java实现

堆

堆排序

思路

如何手写一个堆

1.插入一个数:heap[++size] = x; up(size);

2.求集合当中的最小值heap[1];

3.删除最小值:heap[1]=heap[size];size–;down(1);

4.删除任意一个元素:heap[k]=heap[size];size–;down(k);up(k);//实际上这里只会根据k和父节点大小执行down和up中的一个操作

5.修改任意一个元素:heap[k]=x;down(k);up(k);

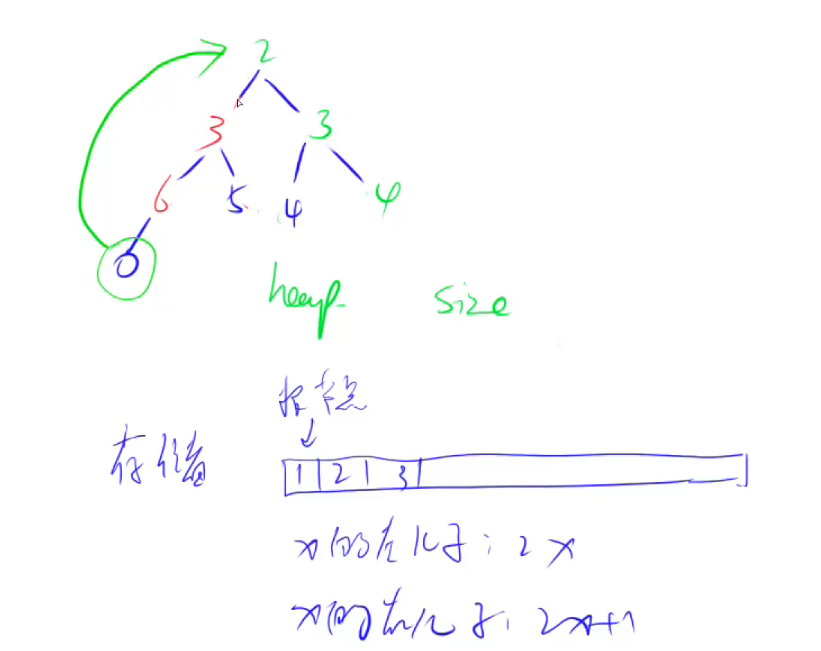
堆是一颗完全二叉树，主要实现两个操作down(x)和up(x)，down的核心思路：判断当前父节点的元素和左右子节点相比是不是最小的和最小的进行交换

创建的时候从n/2开始：n/2开始，还有一个角度可以理解，因为n是最大值，n/2是n的父节点，因为n是最大，所以n/2是最大的有子节点的父节点，所以从n/2往前遍历，就可以把整个数组遍历一遍

代码

import java.util.Scanner;
public class Main{static int N = 100010;static int[] h = new int[N];static int size;//交换函数public static void swap(int x,int y){int temp = h[x];h[x] = h[y];h[y] = temp;}//堆函数核心函数，堆排序函数,传入的参数u是下标public static void down(int u){int t = u; // t用来分身变量//u的左分支下标小于size说明该数存在,然后如果这个数小于t，则让左下标赋值给t,即u的分身 if(u * 2 <= size && h[u * 2] < h[t]) t = u * 2; //u的右分支下标小于size说明该数存在，然后如果这个数小于t，因为可能上面的if语句会重置t，则判断是不是小于新或旧t,//如果小于t的话，就让右下标赋值给t ,即u的分身。if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//如果u不等于t,说明左或者右下标有比较小的值赋值给t了，分身变了if(u != t){//就让u跟t这两个数交换一下位置，让小的数替代u的位置swap(u,t);//然后继续递归t下标小的位置down(t);}}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();for(int i = 1 ; i <= n ; i ++ ) h[i] = scan.nextInt(); //首先将所有数先存入数组中size = n;//长度为n//从n/2的位置开始将数组中的值插入堆中//堆结构是一个完全二叉树，所有有分支的数等于没有分支的数，即最后一排的数量等于上面所有的数//最下面一排没有分支的数不用参与插入，所以从n/2开始进行插入for(int i = n/2 ; i >= 0; --i ) down(i);//就是让他进行向下排序处理 while(m -- > 0){//输出前m小的m个元素System.out.print(h[1] + " "); //每一次输出头节点//因为是数组，删除第一个数复杂，删除最后一个元素比较简单//所以就将最后一个元素将第一个元素覆盖掉，然后删除掉最后一个元素h[1] = h[size--];//然后进行堆排序，对第一个元素进行处理down(1);}}
}

模拟堆

思路

类似链表第k个数

一、ph[] 和 hp[] 的含义
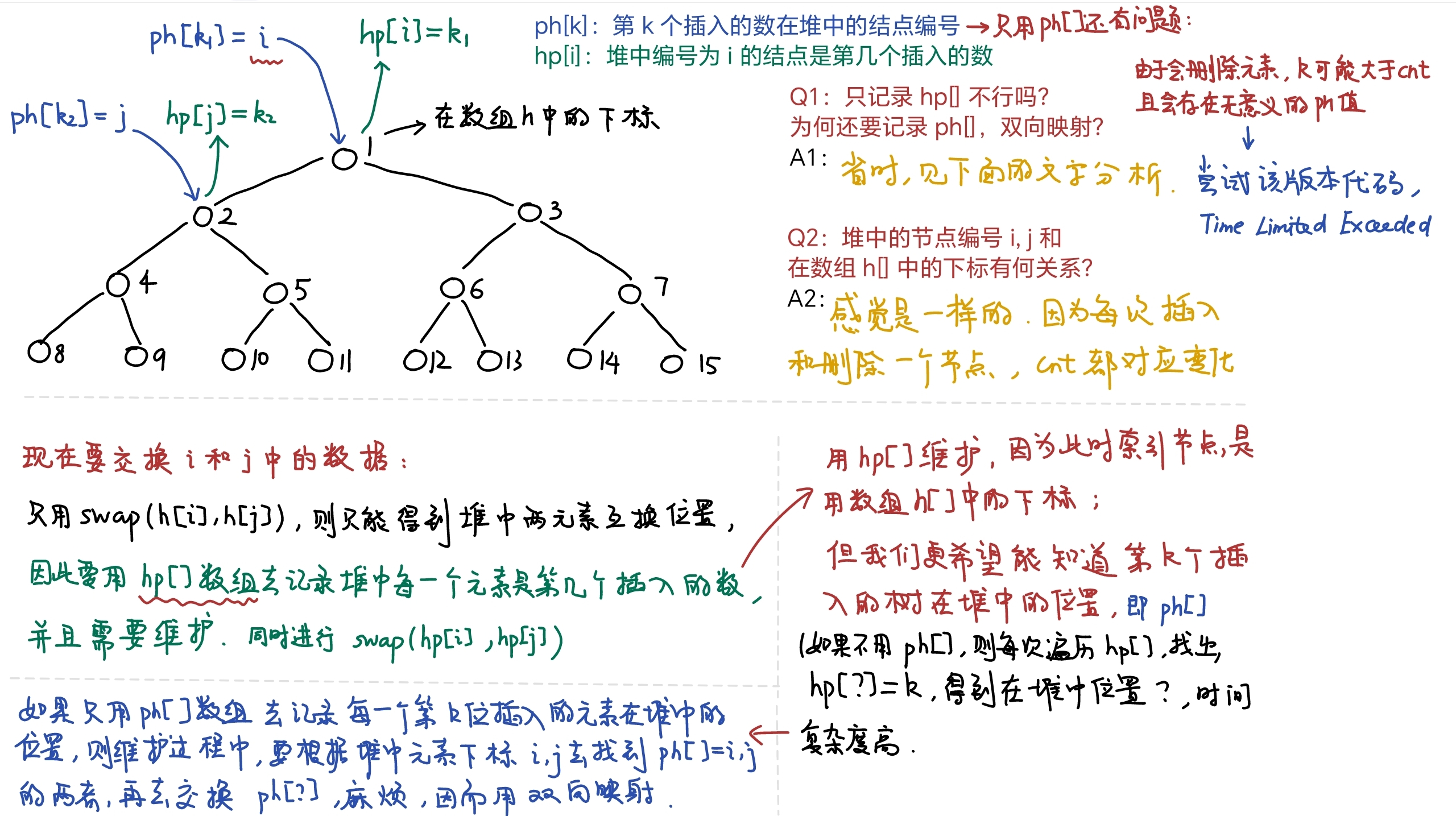
ph[k] = a: 第 k 个插入的数在堆中的下标是 a
hp[a] = k: 堆中下标是 a 的节点是第 k 个插入的数

二、为什么要引入 ph[] 和 hp[]?
AcWing 839. 模拟堆 和 AcWing 838. 堆排序最大的不同在于，需要记录第 k 个插入的数在堆中的位置，因而自然引出 ph[] 数组。

三、只引入 ph[] 为什么不行?
问题是交换节点 a 和 b，同时也需要交换节点 a 和 b 对应的 ph 值，即要找到 ph[i] = a 和 ph[j] = b，进行交换 swap(ph[i], ph[j])，这样就需要遍历 ph[]，时间复杂度高。
注意：ph[] 的有效下标一直到当前插入的数的个数，而非堆中的节点数目cnt，因此需要遍历的点更多，并且删除节点时，也必须删除该节点对应的 ph 值，否则会存在多个 ph[?] = a 的情况。

代码

/*
I x，插入一个数 x；h[++size] = x;up(size);
PM，输出当前集合中的最小值； h[1]
DM，删除当前集合中的最小值（数据保证此时的最小值唯一）； h[1] = h[size--];down(1);
D k，删除第 k 个插入的数； h[k] = h[size--];down(k),up(k)
C k x，修改第 k 个插入的数，将其变为 x；h[k] = x,down(k) ,up(k);
*/
import java.util.Scanner;
public class Main{static int N = 100010,size,m;static int[] h = new int[N];static int[] hp = new int[N];//自身被映射数组static int[] ph = new int[N];//映射数组public static void swap(int[] a,int x,int y){int temp = a[x];a[x] = a[y];a[y] = temp;}public static void head_swap(int x,int y){//这里因为映射数组跟被映射数组是互相指向对方,如果有两个数更换位置，映射下标也要进行更换//ph的下标指向是按顺序插入的下标，hp所对应的值是ph的按顺序的下标，用这两个属性进行交换swap(ph,hp[x],hp[y]);//因为按照顺序插入ph到指向交换了，对应指向ph的hp也要进行交换swap(hp,x,y);//最后两个值进行交换swap(h,x,y);}public static void down(int x){int t = x;//x的分身//判断一下左下标是不是存在//判断一下左下标的值是不是比我t的值小 。那么就将左下标的值赋予t；否则不变if(x * 2 <= size && h[x * 2] < h[t]) t = x * 2;//判断一下右下标的值是不是比我t的值小。那么就将右下标的值赋予t，否则不变if(x *2 + 1 <= size && h[x * 2 + 1] < h[t]) t = x * 2 + 1;if(t != x){//如果x不等于他的分身head_swap(x,t);//那就进行交换顺序down(t);//然后一直向下进行操作}}public static void up(int x){//向上操作，判断一下根节点还不是存在//看一下根节点是不是比我左分支或者右分支的值大，大的话就进行交换while(x / 2 > 0 && h[x / 2] > h[x]){head_swap(x,x/2);x = x / 2;//相当于一直up}}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();size = 0;//size是原数组的下标m = 0;//m是映射数组的下标while(n -- > 0){String s = scan.next();if(s.equals("I")){//插入操作int x= scan.nextInt();size ++;m ++;//插入一个数两个数组的下标都加上1；ph[m] = size;hp[size] = m;//ph与hp数组是映射关系h[size] = x;//将数插入到堆中最后位置up(size);//然后up，往上面排序一遍}else if(s.equals("PM")){ //输出当前集合中的最小值System.out.println(h[1]);}else if(s.equals("DM")){//删除当前集合中的最小值//因为需要用到映射数组与被映射数组,因为需要找到k的位置在哪里，需要让映射的顺序，//因为如果用size，size是会随时改变的，不是按顺序的，因为会被up或者down顺序会被修改head_swap(1,size);//将最后一个数替换掉第一个最小值元素，然后数量减1，size--size--;down(1);//插入之后进行向下操作，因为可能不符合小根堆}else if(s.equals("D")){//删除当前集合中第k个插入得数int k = scan.nextInt();k = ph[k];//ph[k] 是一步一步插入映射的下标，不会乱序，head_swap(k,size);//然后将k与最后一个元素进行交换，然后长度减1，size--size--;up(k);//进行排序一遍，为了省代码量，up一遍down一遍。因为只会执行其中一个down(k);}else{int k = scan.nextInt();int x = scan.nextInt();k = ph[k];//ph[k] 是一步一步插入映射的下标，顺序是按照插入时候的顺序h[k] = x;//然后将第k为数修改为数xup(k);//up一遍，down一遍down(k);}}}
}