当前位置： 首页 > news >正文

位置编码演进史：SIN → ALiBi → RoPE → PI → NTK → YARN

news 2025/11/10 14:59:24

​

前言：假期翻看了一年前总结的有关位置编码的笔记，发现在某些角度上有了新的理解，本次也分享出来。本文讲解的顺序是：SIN->ALiBi->RoPE->PI->NTK->YARN，公式较多，建议pc端食用。

一、SIN（正弦位置编码）

图1-1：正弦位置编码形式的由来

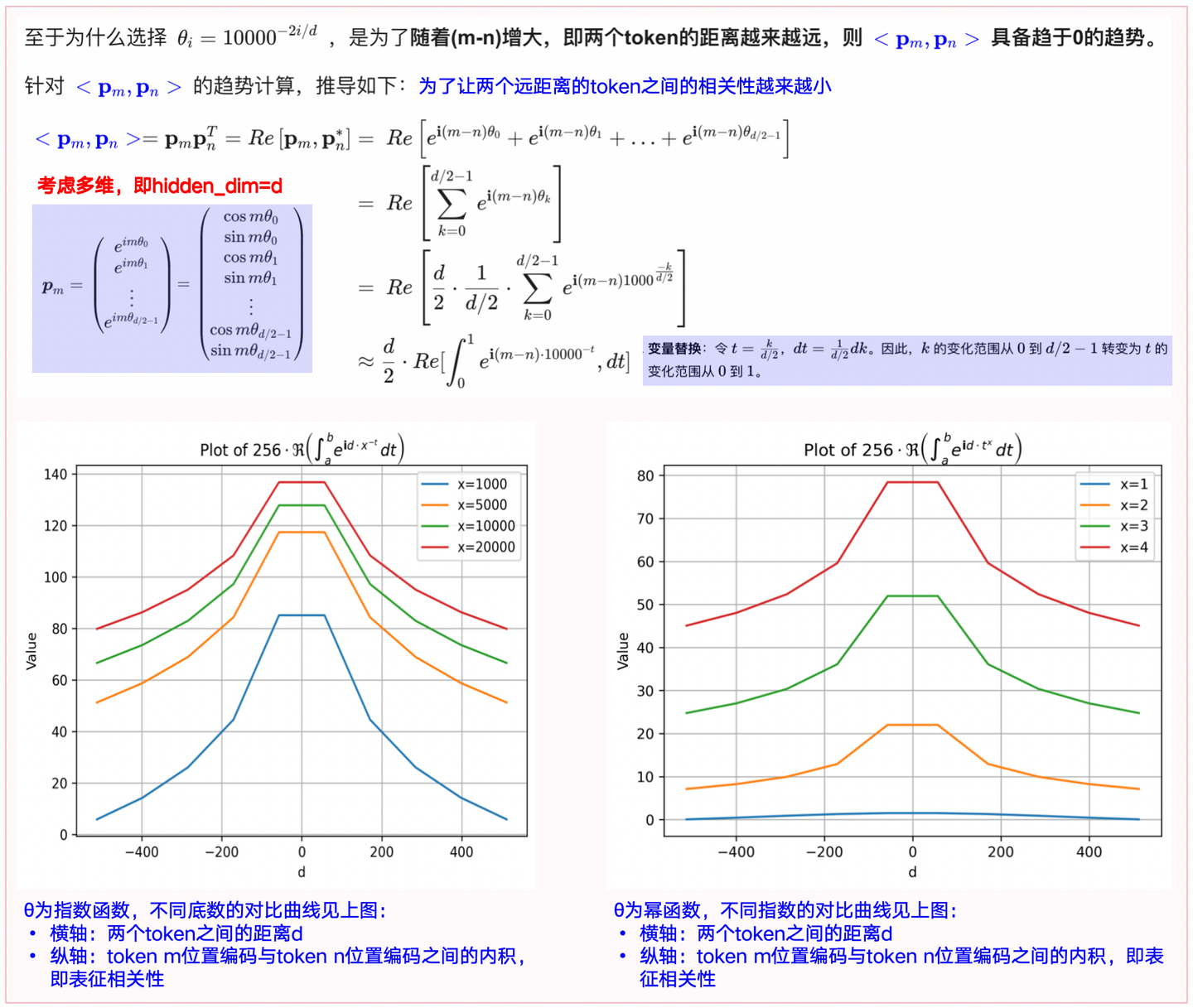
图1-2：正弦位置编码中θ的由来

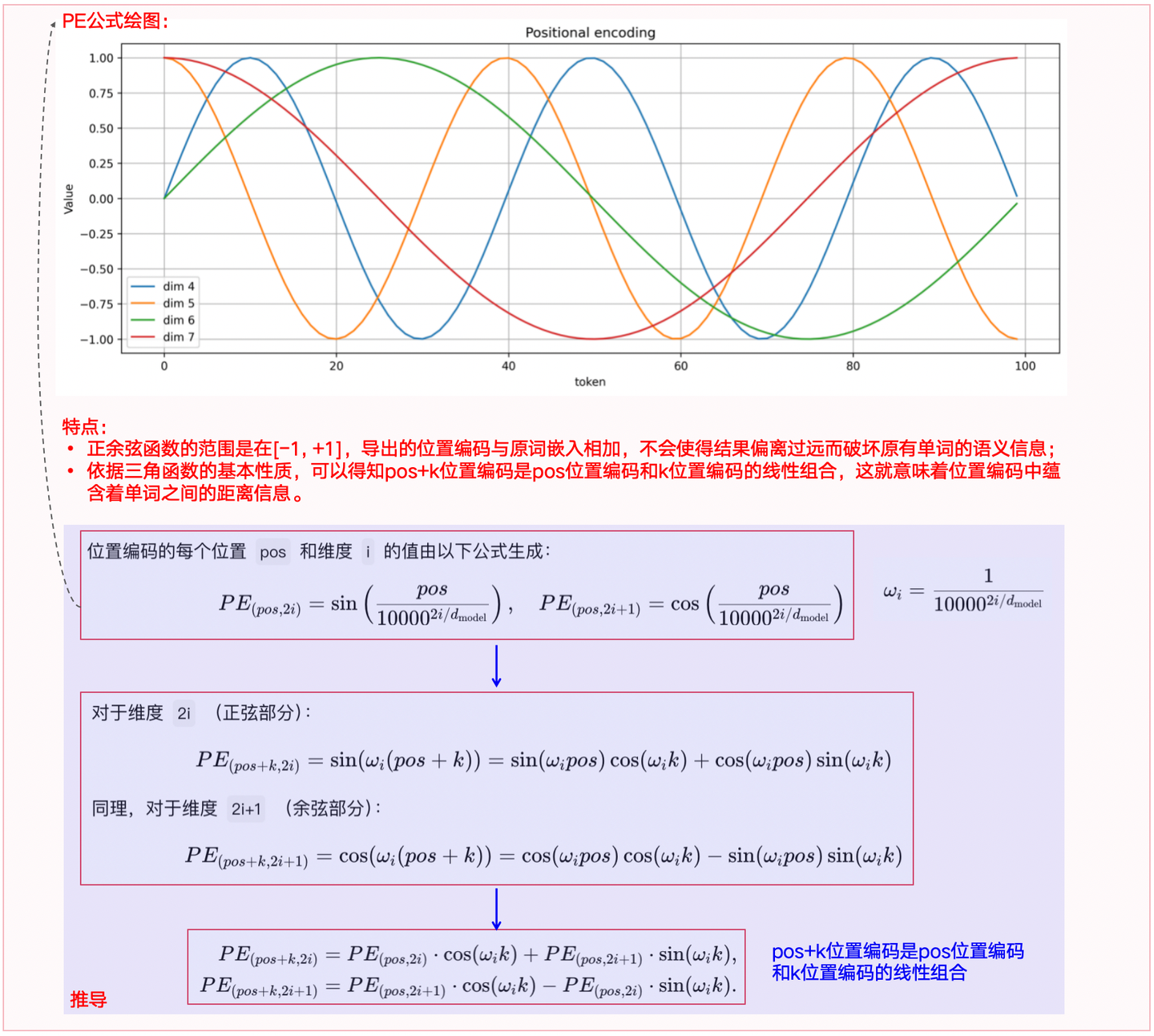
图1-3：正弦位置编码的特点+推导

**缺点：**sin位置编码表示相对位置关系时仍然比较间接。

二、ALiBi（Attention with Linear Biases）

**思路：**ALiBi（基于线性偏差的注意力机制） 不向word embedding中添加positional embedding，而是"根据token之间的距离给 attention score 加上一个预设好的偏置矩阵"，即直接引入相对位置。

**举例：**两个token之间存在一个相对位置差1，就加上一个 -1 的偏置，如果token之间的距离越远则这个负数就越大，代表它们之间的相关性更低。

图2-1：ALiBi如何引入MHA中

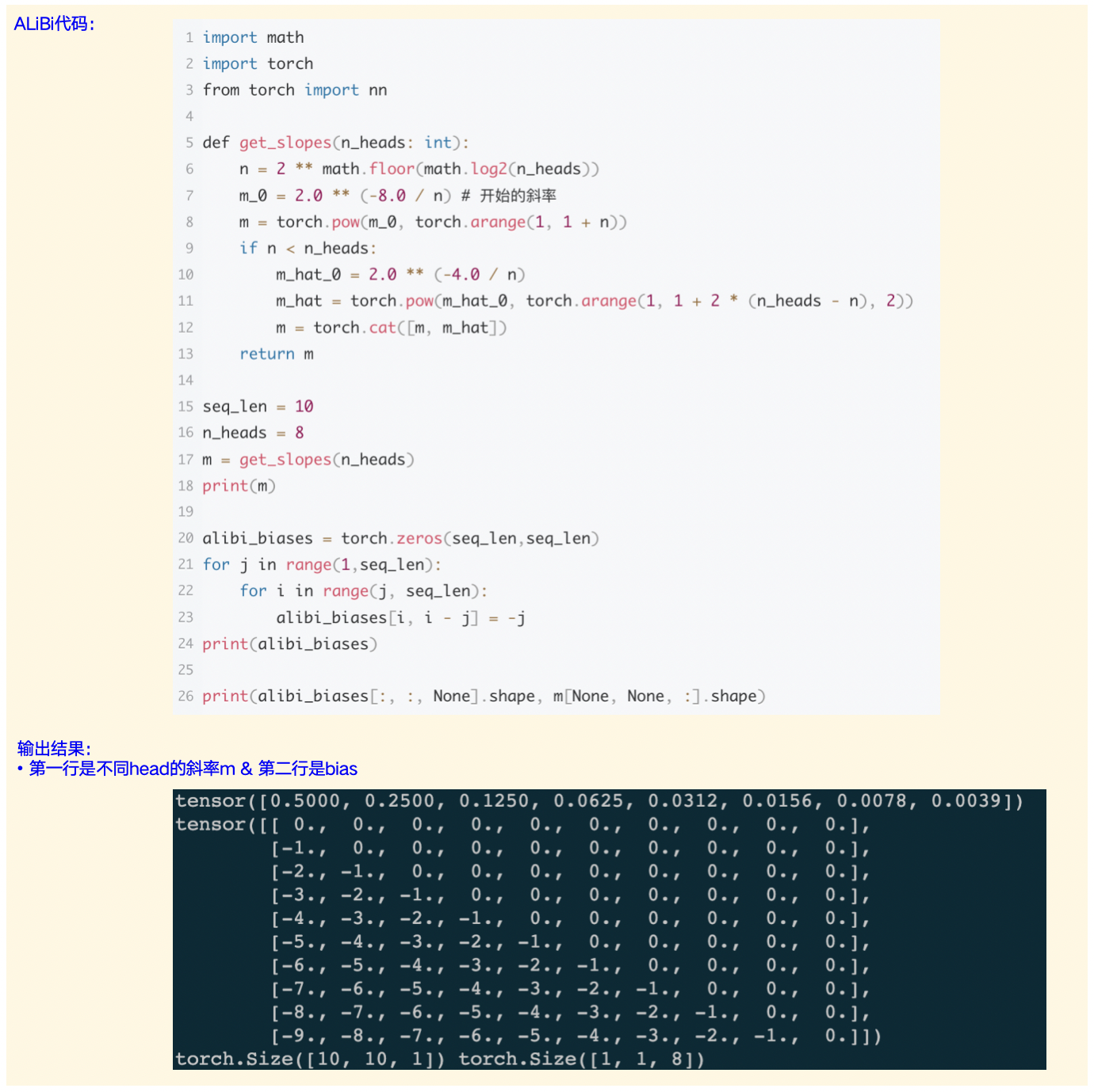
图2-2：ALiBi的示例代码和结果

三、RoPE（Rotary Position Embedding）

2021年，RoPE（旋转位置编码）诞生，它借助了复数的思想，出发点是通过绝对位置编码的方式实现相对位置编码。

**设计思路：**在NLP中，通常会通过向量q和k的内积来计算注意力系数（ATTN），如果能够对q、k向量注入位置信息，然后用更新的q、k向量做内积就能丝滑地引入位置信息了。

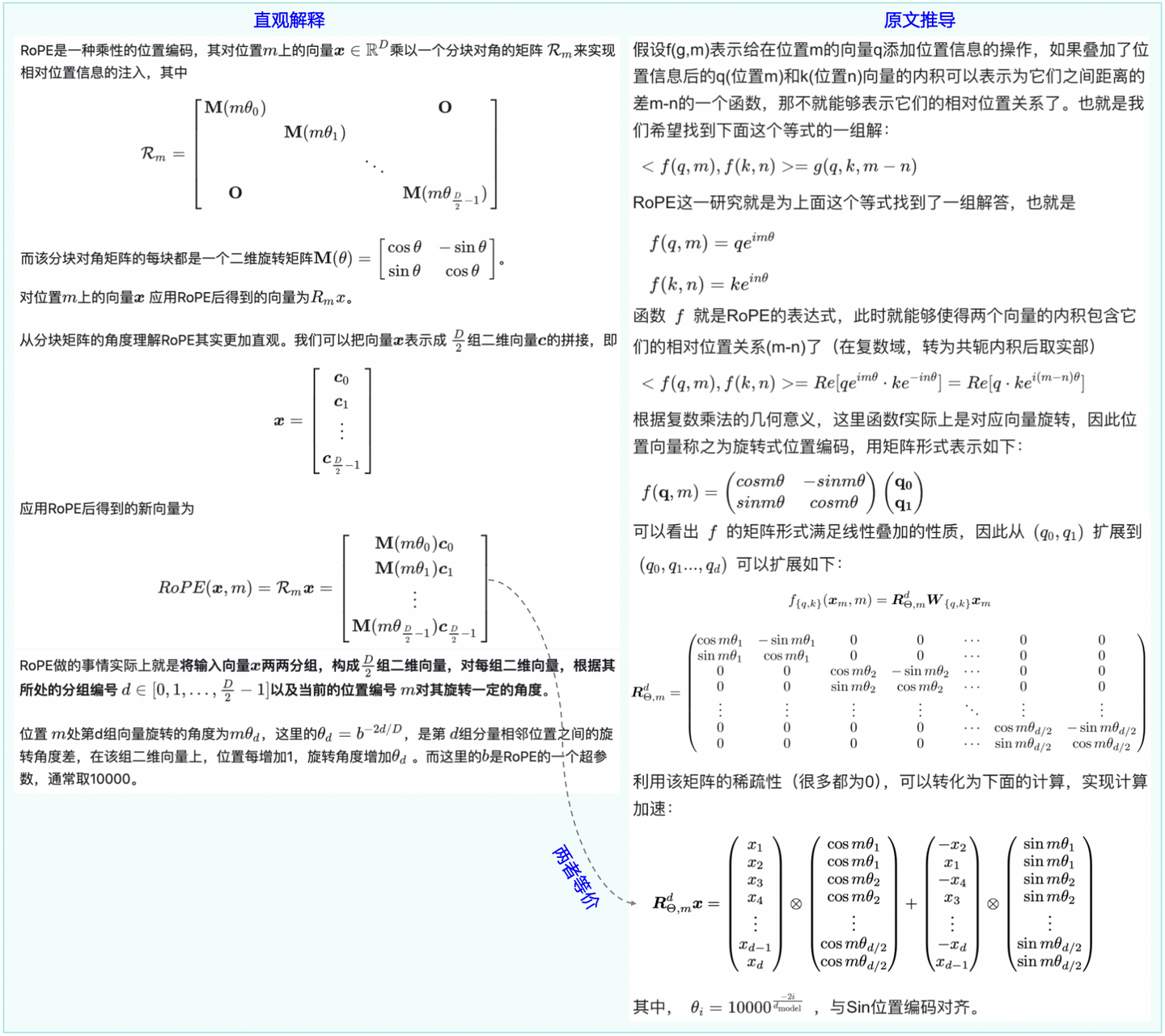
图3-1：RoPE的两种解释（左：直观解释，右：原始推导）

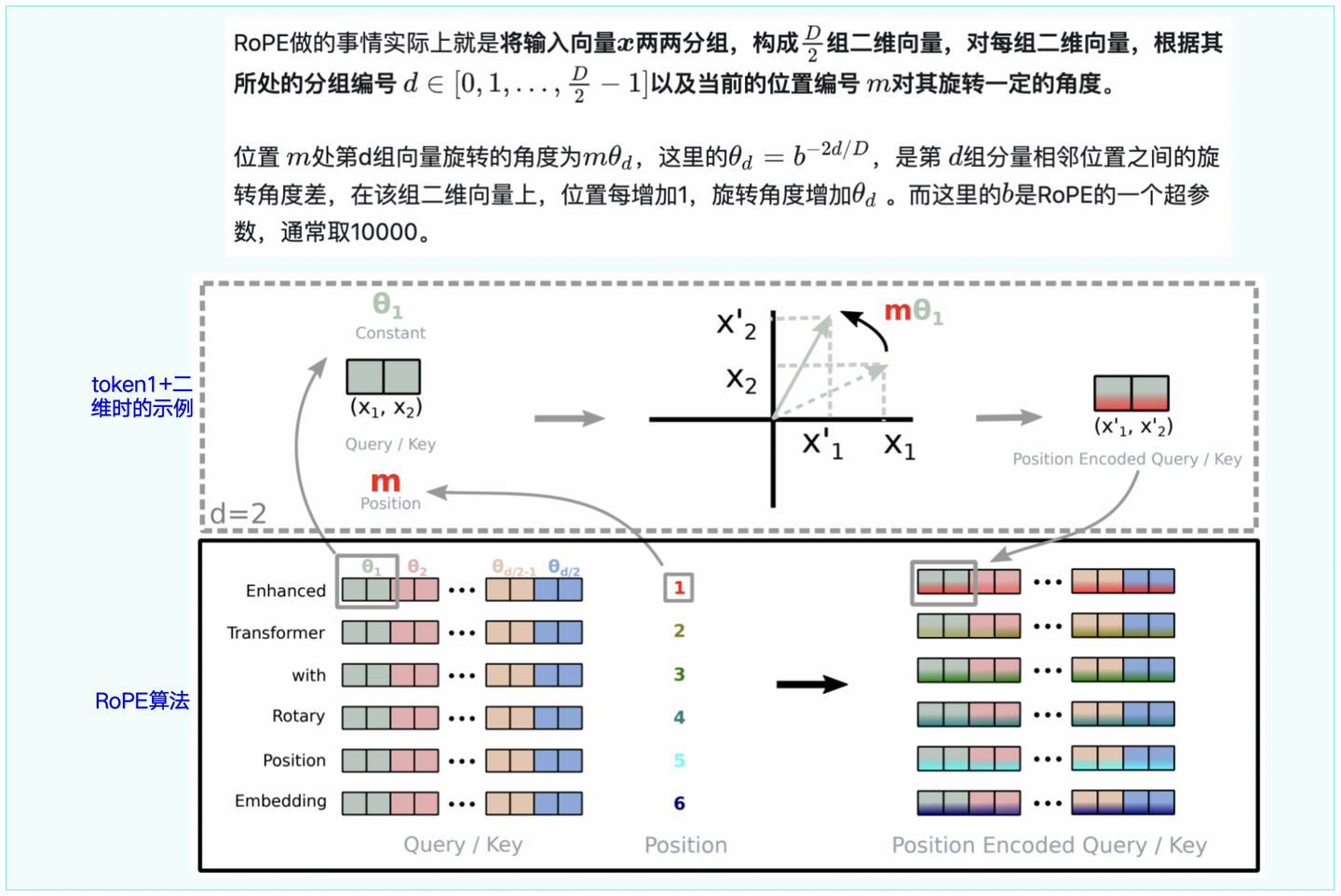
图3-2：RoPE的操作示意图

在transformer模型中RoPE如何使用：

# 1. 首先进行普通的Query和Key的线性变换
q = x @ Wq  # [batch_size, seq_len, d_model] -> [batch_size, seq_len, d_head]
k = x @ Wk# 2. 然后对q和k应用RoPE
q_rotated = apply_rotary_pos_emb(q, position_ids)
k_rotated = apply_rotary_pos_emb(k, position_ids)def apply_rotary_pos_emb(q, position_ids):# q shape: [batch_size, seq_len, dim]seq_len = q.shape[1]dim = q.shape[2]# 生成位置编码的角度theta = 1.0 / (10000 ** (torch.arange(0, dim, 2).float() / dim))# 计算每个位置的旋转角度pos_emb = position_ids.unsqueeze(-1) * theta# 生成cos和sin值cos = torch.cos(pos_emb)sin = torch.sin(pos_emb)# 将q分成两半，便于旋转操作q_even = q[:, :, 0::2]  # 偶数维度q_odd = q[:, :, 1::2]   # 奇数维度# 应用旋转变换q_out_even = q_even * cos - q_odd * sinq_out_odd = q_odd * cos + q_even * sin# 重新组合q_out = torch.stack([q_out_even, q_out_odd], dim=-1)q_out = q_out.flatten(-2)return q_out

四、PI（Position Interpolation）

PI（位置插值）是基于旋转位置编码RoPE进行改进，优化了外推性的问题：使用RoPE，以长度为L训练完成模型后，当输入超过L会发生性能剧烈下降，一些论文提出可以通过给模型喂一些长度大于L的输入来微调模型，进而逐步将原始窗口长度扩大，但其代价和成效不佳（实验结果如下图4-1）。

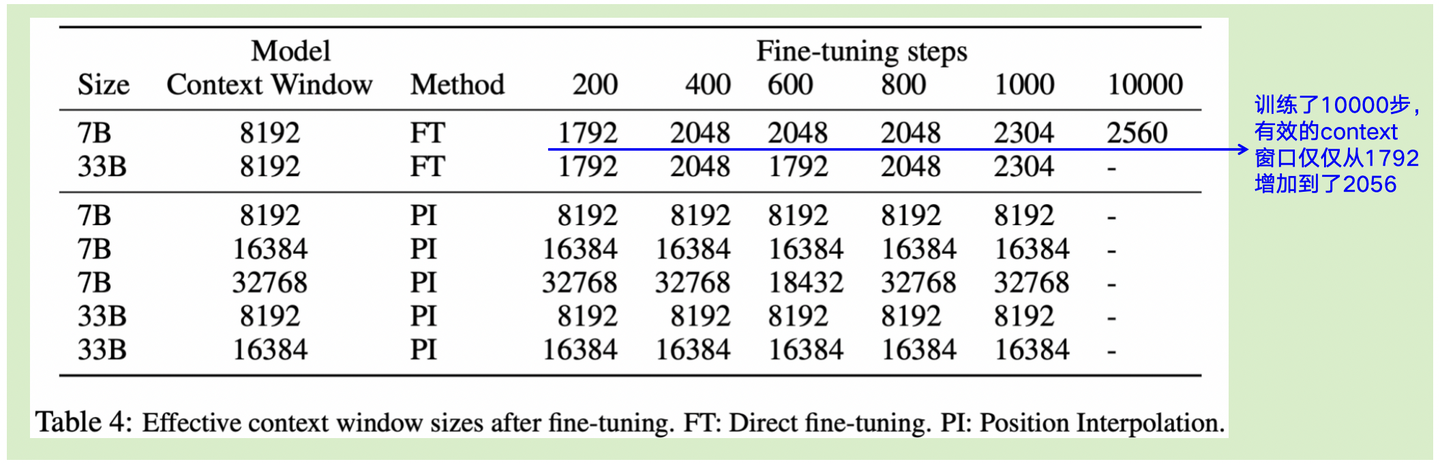
图4-1：以微调来提升上下文窗口的实验

**思路：**将超出L部分编码值压缩到L内。

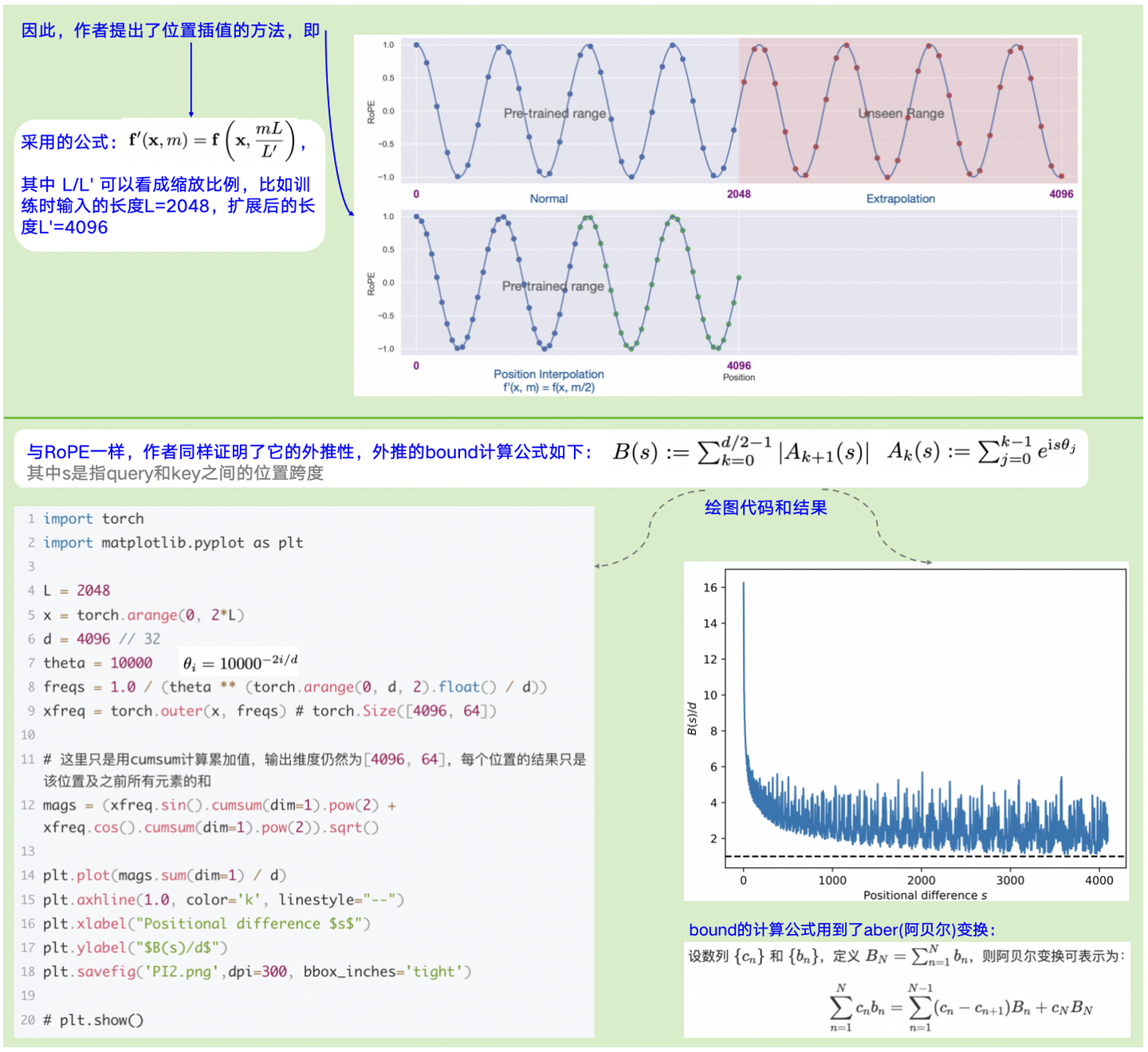
图4-2：PI思路+公式+外推性证明

注意：上图4-2中，外推bound的计算是用了aber变换，完整证明见原论文。

论文针对外推（Extrapolation）和内插（ interpolation），也给出了一些实验，见图4-3：

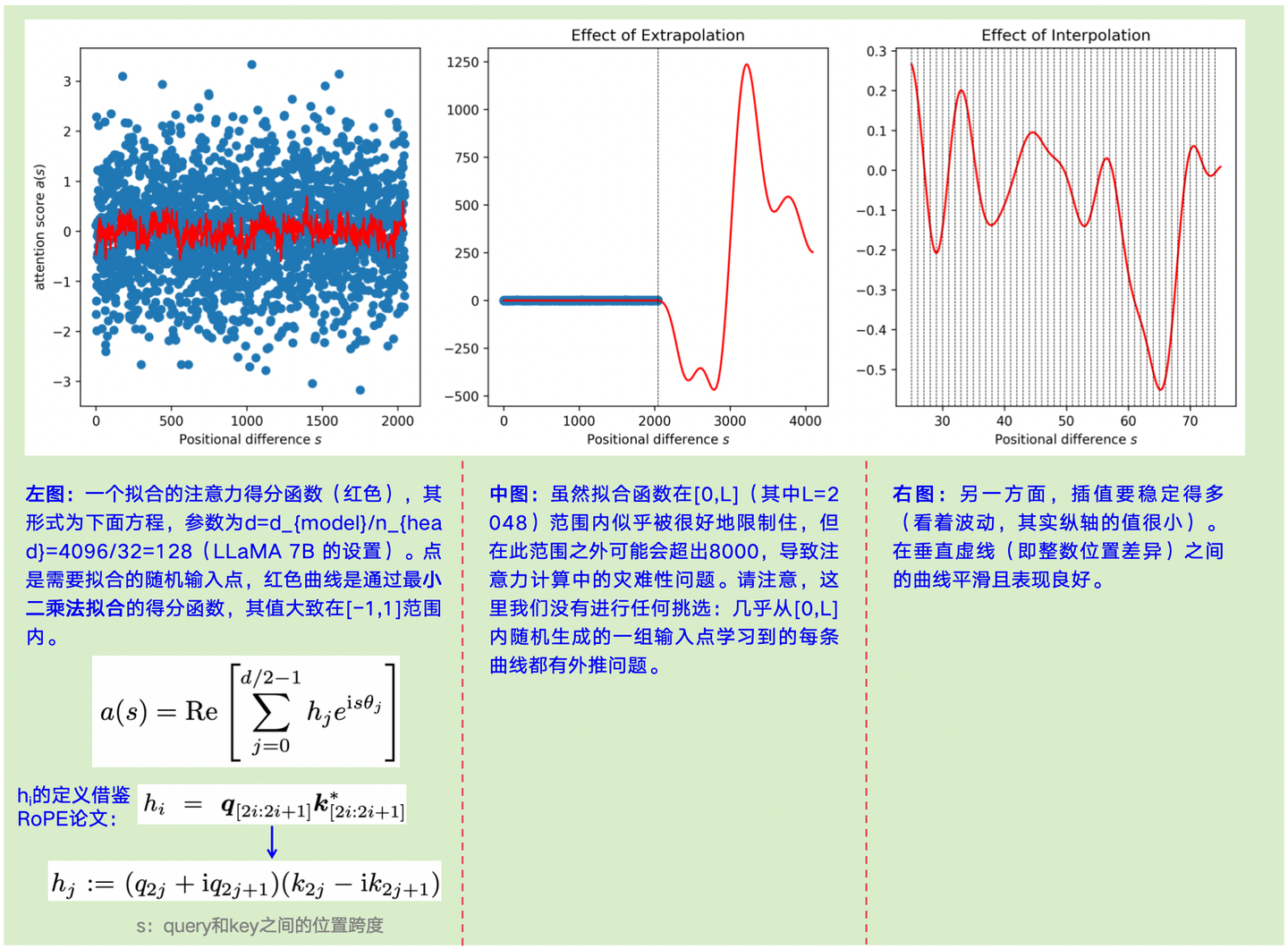
图4-3：外推和内插的可视化实验

图4-3的实验代码如下：

import torch
import matplotlib.pyplot as plt# build basis function
d = 4096 // 32
theta = 10000
# Frequency computation
freqs = 1.0 / (theta ** (torch.arange(0, d, 2).float() / d))
# construct basis function
L = 2048
x = torch.arange(0, L)
# basis functions
xfreq = torch.outer(x, freqs)
print(xfreq.shape)
y = torch.randn(x.shape[0])
# do linear regression
X = torch.cat([xfreq.sin(), xfreq.cos()], dim=1)eps = 1e-5  # small regularization term
# 实现线性回归使得X*coeffs很好的逼近y，最终求解coeffs
coeffs = torch.linalg.solve(X.t() @ X + torch.eye(X.shape[1]) * eps, X.t() @ y)x2 = torch.arange(0, 2*L)
xfreq2 = torch.outer(x2, freqs)
X2 = torch.cat([xfreq2.sin(), xfreq2.cos()], dim=1)
y2 = X2 @ coeffsx3 = torch.arange(25, 75, 0.125)
xfreq3 = torch.outer(x3, freqs)
X3 = torch.cat([xfreq3.sin(), xfreq3.cos()], dim=1)
y3 = X3 @ coeffsplt.figure(figsize=(16, 5))plt.subplot(1, 3, 1)
plt.plot(x2[:L], y2[:L], "r")
plt.scatter(x, y)
plt.ylabel("attention score $a(s)$")
plt.xlabel("Positional difference $s$")plt.subplot(1, 3, 2)
plt.plot(x2, y2, "r")
plt.scatter(x, y)
plt.axvline(L, color="k", linestyle="--", linewidth=0.5)
plt.title("Effect of Extrapolation")
plt.xlabel("Positional difference $s$")plt.subplot(1, 3, 3)
plt.plot(x3, y3, "r")
for i in range(25, 75):plt.axvline(i, color="k", linestyle="--", linewidth=0.5)
plt.title("Effect of Interpolation")
plt.xlabel("Positional difference $s$")
plt.savefig('PI.png',dpi=300, bbox_inches='tight')
# plt.show()

五、NTK（Neural Tangent Kernel）

**现状：**PI会在扩展倍数特别大时显著降低位置编码区分不同位置的能力，这种现象称之为高频信息的损失。

图5-1：PI的缺点和问题所在

**NTK（Neural Tangent Kernel）的思想：**高频外推+低频内插，即将 \color{blue}{\theta_{i}=b^{-2i/d}改为\theta_{i}=(b\cdot S{d/(d-2)}){-2i/d}}，也就是改变了基底（这里b=10000， \color{blue}{S=L’/L} ）。推导见图5-2和图5-3：

图5-2：NTK推导1——位置编码的本质是求位置n的β进制数

图5-3：NTK推导2——统一高频外推和低频内插

在代码上修改很小，如下11行：

from transformers import AutoModelForCausalLM, AutoTokenizer, GenerationConfig
import torch
import transformersold_init = transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__
def ntk_scaled_init(self, dim, max_position_embeddings=2048, base=10000, device=None):#The method is just these three linesmax_position_embeddings = 16384a = 8 #Alpha valuebase = base * a ** (dim / (dim-2)) #Base change formula # NTK-Awareold_init(self, dim, max_position_embeddings, base, device)
transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.__init__ = ntk_scaled_init

六、YARN（Yet another RoPE extensioN method）

6.1 波长的引入

在某个维度i下，波长被定义为： \lambda_{i}=\frac{2π}{\theta_{i}}=\frac{2\pi}{b^{-2i/d}}=2\pi b^{2i/d} ，因此，有如下结论：

  • 波长可描述为：在维度i处嵌入的旋转位置执行全旋转2π所需的token长度。
  • 维度越高波长越长。

证明见下图6-1：

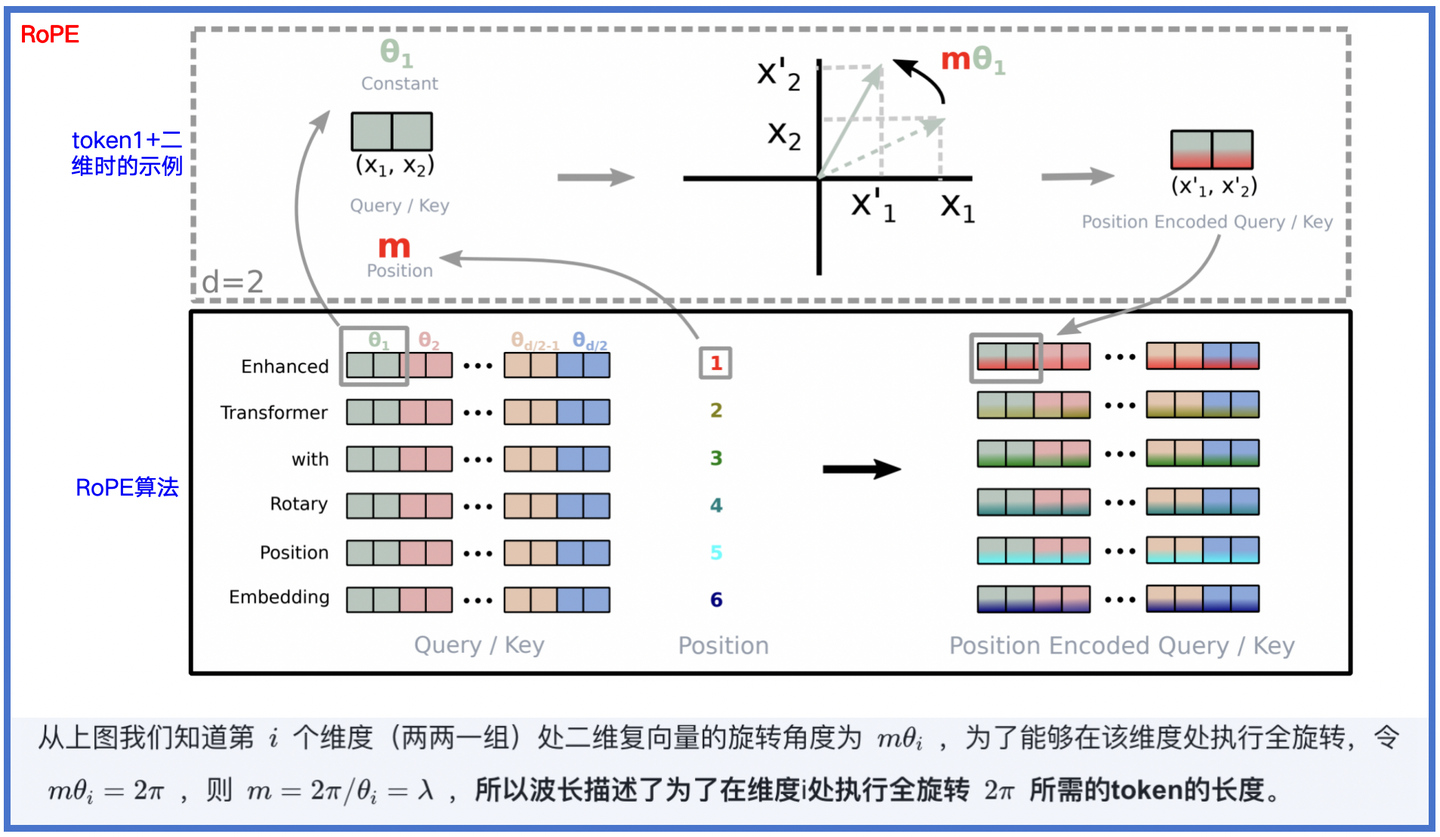
图6-1：波长描述了维度i处执行全旋转2π所需的token长度

像PI和NTK这种类型的插值方案不关心波长的维数，可以将其称为“盲”插值方法（blind interpolation），因为它们面对所有RoPE隐藏维度没有做任何针对性的处理。而本次要讲解的YaRN，可将其归类为“有针对性的”插值方法，即对RoPE的不同维度做出不同处理。

6.2 NTK-by-parts（局部NTK）

关于RoPE中不同维度的波长，有如下结论：存在某些维度i，其波长 \lambda_{i} 大于在预训练期间看到的最大上下文长度L。也就是说：在训练期间，存在某一个维度，旋转一圈后超过了token最大上下文长度L。具体每个维度的波形可以参考图1-3，即Sin方法的绘图，其中 d=20,pos\in{[0,100]} 。

  • 如果某些维度的波长大于上下文长度L（ \lambda_{i}>L ），这说明该维度无法执行全旋转。在这种情况下，由于维度在预训练期间至少不会完全旋转一次，如果我们选择第一个token作为基准，那么在预训练期间每隔一个token到它的距离是唯一的，NTK可以用来确定它的绝对位置信息。
  • 相反，如果某个维度波长小于L（ \lambda_{i}<L ），那该维度就执行了至少一次全旋转，我们就无法在这个维度描述绝对距离，只能描述相对位置信息。

因此，作者认为，不要对『只编码相对位置信息的维度』（ \lambda_{i}<L ）进行内插破坏，因为它们对于模型区分附近token的相对顺序至关重要。同时，应该始终对仅编码绝对位置信息的维度（ \lambda_{i}>L ）进行内插，因为较大的距离将超出之前模型能够编码的距离。综上，可以制定一种考虑以上所有因素的显式且有针对性的插值方法，即：

  • 如果波长远小于L，此时编码了相对位置的维度，因此不进行内插；
  • 如果波长大于L，此时编码了绝对位置的维度，应该进行内插以防止超出绝对位置的最大可编码范围；
  • 波长介于上述之间的维度，采用NTK-aware方法。

公式如下：

图6-2：NTK-by-parts公式

6.3 YARN

图6-3：YARN的提出

在实际使用过程中，为了实现该公式，只需要将m位置和n位置的旋转位置嵌入各自缩放为原来的 1/\sqrt{t} 即可。

6.4 Dynamic NTK

在NTK中 S=\frac{L’}{L} ，在推理时，这里的 S 是固定的（ L’ 是固定的扩展上下文大小， L 是预训练时候的最大上下文长度）。但是，这可能导致推理的序列长度 <L 时会损失模型性能。

因此，作者提出了动态的NTK，公式为 \color{blue} {S=\max({1,{l’/L}})} ，其中 l’ 为当前输入的长度，这就允许模型在达到训练的上下文限制时较为缓慢地退化性能，避免了骤降。

如果不好理解，进一步解释分析如下：

图6-4：Dynamic NTK的分析和公式解释

七、总结

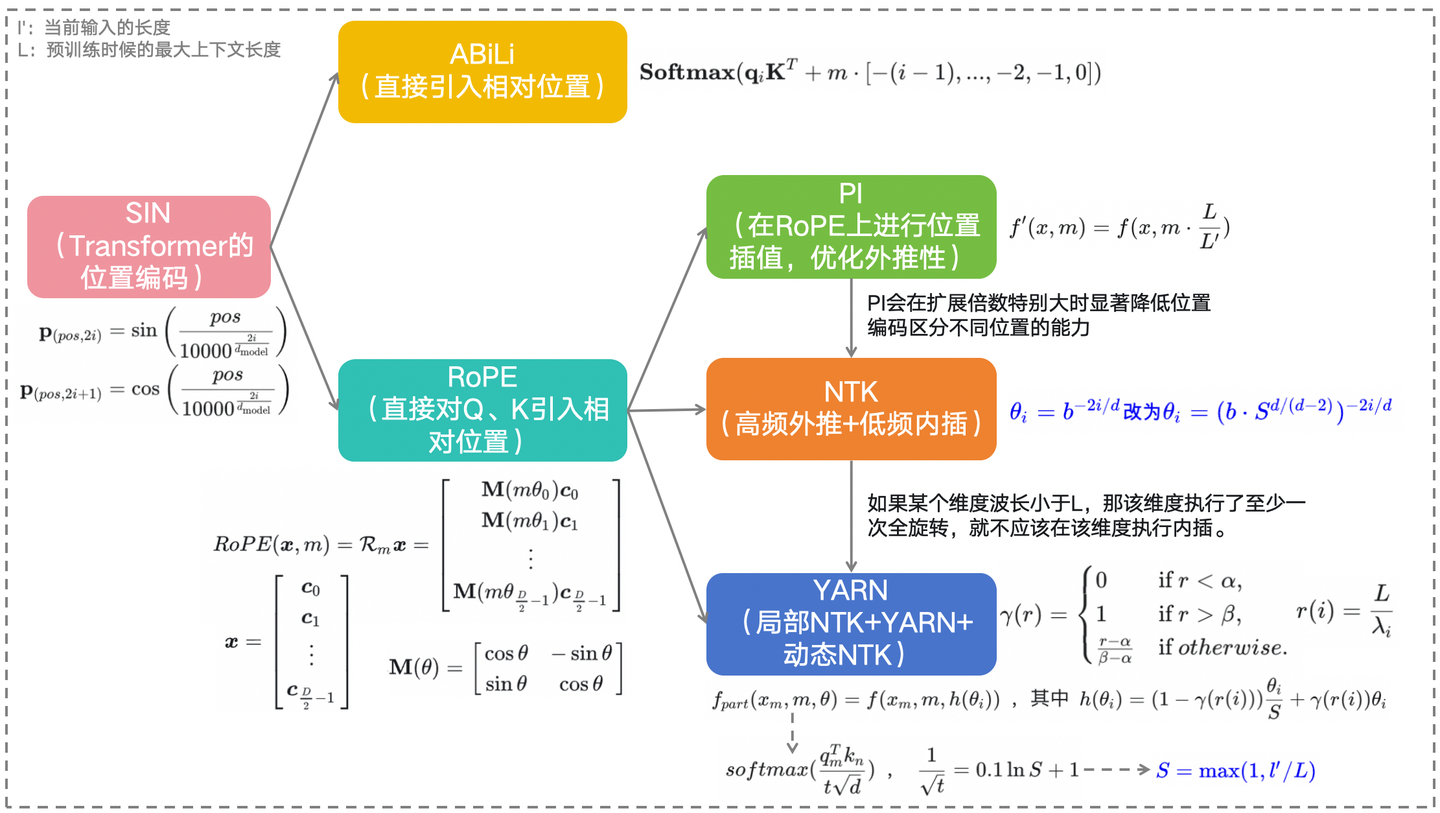
图7-1：六种位置编码方法总结

八、参考文献

来源：https://zhuanlan.zhihu.com/p/1894384438206505105

  • SIN：https://arxiv.org/pdf/1706.03762
  • RoPE：https://arxiv.org/pdf/2104.09864
  • ALiBi：https://arxiv.org/pdf/2108.12409
  • PI：https://arxiv.org/pdf/2306.15595
  • Linsight：理解LLM位置编码:RoPE
  • barely：上下文长度扩展：从RoPE到YARN
  • https://www.reddit.com/r/LocalLLaMA/comments/14lz7j5/ntkaware_scaled_rope_allows_llama_models_to_have/, https://zhuanlan.zhihu.com/p/704569344
  • Cyril-KI：LLM上下文长度扩展方案：NTK-aware interpolation
  • https://zhuanlan.zhihu.com/p/897061302,
  • YARN：https://arxiv.org/pdf/2309.00071
http://www.dtcms.com/a/590608.html

相关文章：

  • 网站建设是必须的吗苏州工业园区两学一做教育网站
  • 鹤峰网站制作win7下使用wordpress
  • ThreadLocal中key为什么是弱引用，value为什么是强引用
  • 天津刘金鹏做网站网站手机版管理链接
  • 天津建设协会网站首页什么叫一级域名二级域名
  • YesPlayMusic v0.4.10 | 一款网易云第三方开源音乐播放器，同时支持切换其他酷我、QQ等音源
  • 手机网站建设浩森宇特网络营销的优势和劣势
  • 哪里学网站建设推广用wordpress建网站
  • 企业网站开发成都网页开发者选项在哪里
  • AI空间低配版？没有新品也能体验，极空间部署Foxel网盘
  • 如何建立内部网站怎么做hello官方网站
  • 常见的营销手段深圳网络营销优化
  • 重庆市公共资源交易中心专业做seo的网站
  • 企业门户网站源码下载做网站协调
  • 网站图片轮播怎么弄网站前端切图做多个页面
  • 目字形布局结构的网站做网站id
  • Modbus通信协议详解：工业自动化的经典协议
  • C++初始继承，继承中构造、析构顺序
  • PyTorch深度学习实战01：全流程体验深度学习
  • 网站建设的人员组织专业网站建设策划
  • 网站首页代码怎么做相亲网站怎么建设
  • 经典网站设计风格seo 0xu
  • 江苏 江苏省住房和城乡建设厅网站公示区信息查询方法
  • 做网站算 自由职业者谷歌云wordpress
  • 【Linux网络】多路转接select
  • C++的基础语法篇一
  • 苏州网站推广如何使用aspx做电影网站
  • 视差设计网站深圳移动网站建设
  • 上贵州省建设厅的网站哪里网站建设专业
  • 网站建设电话营销培训ppt课件百度门店推广