代码随想录 Q85.摆动序列

方法一：贪心解法。

1.题目要求：从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

2.以示例2为例：如下图所示，局部最优能推出全局最优，并且举不出反例，可以试试贪心。

（1）局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

（2）全局最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

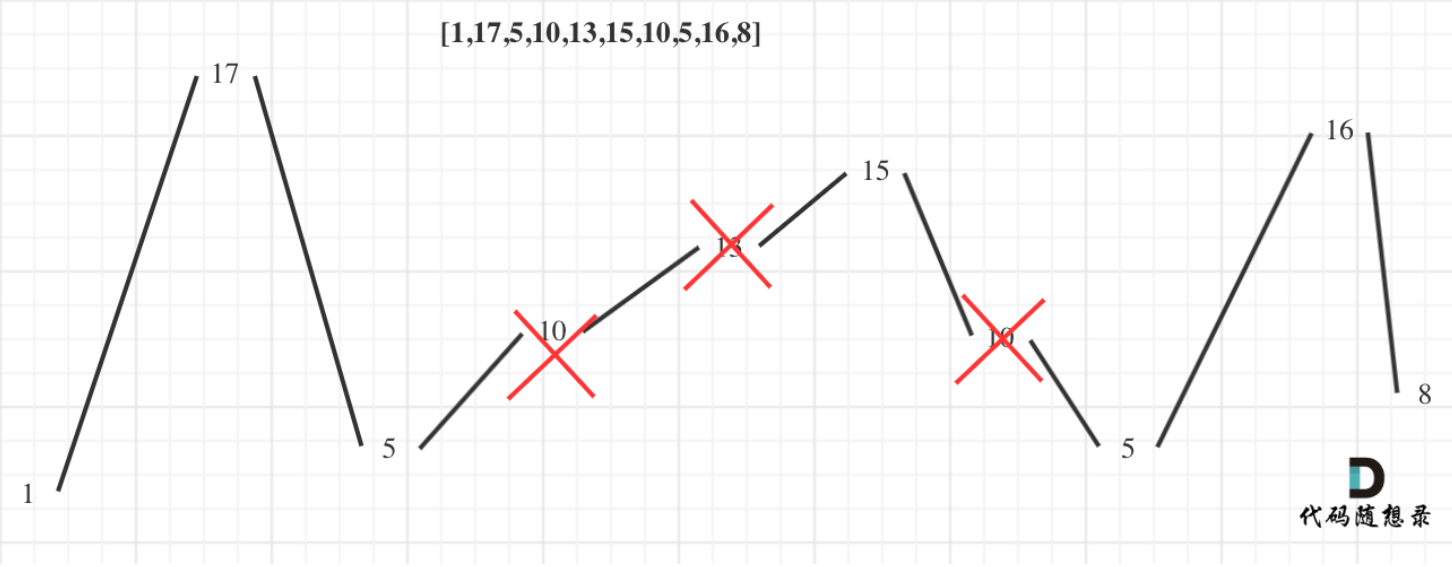
3.实际操作中，不需要删除节点。因为题目求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）。

4.贪心思路：让峰值尽可能保持峰值，然后删除单一坡度上的节点。在计算是否有峰值的时候，已知遍历的下标i，计算prediff（nums[i] - nums[i - 1]）和curdiff（nums[i + 1] - nums[i]），如果prediff < 0 && curdiff > 0或者prediff > 0 && curdiff < 0此时就有波动需要统计。

5.本题需要考虑三种情况：上下坡中有平坡、数组首尾两端和单调坡中有平坡。

（1）情况一：上下坡中有平坡。例如[1,2,2,2,2,1]这样的数组，如下图所示，它的摇摆序列长度为3，也就是说在删除的时候，要么删除左边的三个2，要么删除右边的三个2。

<