《C++ STL容器适配器:stack和queue的实现机制与应用场景》
目录
引言
一、容器适配器的本质
1.1 设计哲学
1.2 底层容器选择策略
二、Stack的工程实践
2.1 核心操作与内存模型
2.2 典型应用场景
场景1:括号匹配验证
场景2:函数调用栈模拟
练手算法题:
155. 最小栈 - 力扣(LeetCode)
栈的压入、弹出序列_牛客题霸_牛客网
150. 逆波兰表达式求值 - 力扣(LeetCode) 后缀表达式
1. 快速判断运算符
2. 性能分析
224. 基本计算器 - 力扣(LeetCode)(给一个中缀计算结果)拓展题目
三、队列
3.1 创建队列对象
3.2 六大核心方法
队列的三大典型应用场景
3.3 消息队列实现
3.4 广度优先搜索(BFS)
3.5 实时数据缓冲
栈的模拟实现:
队列的模拟实现:
编辑
deque实现思想:
deque优缺点
让我们先来看看库中的stack和queue
引言
在C++标准模板库(STL)中,stack和queue作为典型的容器适配器,是每位开发者必须掌握的核心数据结构。它们看似简单,却蕴含着程序设计中的重要哲学——通过限制操作来实现特定的数据管理策略。本文将从底层实现原理出发,结合工程实践中的典型应用场景,揭示这两种线性容器的本质特性。
一、容器适配器的本质
1.1 设计哲学
stack和queue并非独立容器,而是构建在其他序列容器(如deque、list)之上的适配器。这种设计体现了软件工程中的"组合优于继承"原则,通过限制基础容器的接口来实现特定的访问策略。
template <class T, class Container = deque<T>>
class stack;
template <class T, class Container = deque<T>>
class queue;1.2 底层容器选择策略
stack默认使用deque:支持快速的首尾插入/删除操作(O(1)时间复杂度)
queue默认使用deque:同时需要高效的头部删除和尾部插入
可替换容器类型验证:
vector(仅适用于stack)
list(适用于两者)
二、Stack的工程实践
2.1 核心操作与内存模型
stack<int> s;
s.push(1); // 压栈 O(1)
s.emplace(2); // 原地构造 C++11
s.top(); // 查看栈顶 O(1)
s.pop(); // 出栈 O(1)内存增长示意图:
[栈底] -> 元素1 -> 元素2 -> ... -> 元素N [栈顶]2.2 典型应用场景
场景1:括号匹配验证
解题思路是:
栈的使用:栈的“后进先出”特性完美匹配括号的嵌套关系。例如,遇到左括号时压栈,遇到右括号时检查栈顶是否匹配。
#include <stack>
using namespace std;
bool isValidParentheses(const string& s) {
stack<char> stk;
for (char c : s) {
if (c == ')' || c == ']' || c == '}') { // 当前字符是右括号
if (stk.empty()) return false; // 栈为空,无法匹配
// 根据右括号类型检查栈顶是否匹配
if ((c == ')' && stk.top() != '(') ||
(c == ']' && stk.top() != '[') ||
(c == '}' && stk.top() != '{')) {
return false;
}
stk.pop(); // 匹配成功,弹出栈顶左括号
} else {
stk.push(c); // 左括号直接入栈
}
}
return stk.empty();
}场景2:函数调用栈模拟
struct FunctionCall {
int returnAddress;
vector<int> parameters;
};
stack<FunctionCall> callStack;
// 函数调用
callStack.push({0x0040A2B0, {1, 2, 3}});
// 函数返回
FunctionCall ret = callStack.top();
callStack.pop();练手算法题:
155. 最小栈 - 力扣(LeetCode)
解题思路:
提供两个栈,一个栈用来存原数_st,一个栈用来存小值_minst
_minst:在空栈的时候先和_st一样存入一个值,后续入栈时都需要与_minst栈顶比较,
入栈的值比当前_minst.top()值小或等于则继续入这个_minst栈。
代码实现:
class MinStack { public: MinStack() { } void push(int val) { _st.push(val); if(_minst.empty() || _minst.top() >= val) { _minst.push(val); } } void pop() { if(_minst.top() == _st.top()) { _minst.pop(); } _st.pop(); } int top() { return _st.top(); } int getMin() { return _minst.top(); } stack<int> _st; stack<int> _minst; };
栈的压入、弹出序列_牛客题霸_牛客网

解题思路:
1.先按入栈序列入栈
2.栈顶元素和出栈序列是否匹配
a.如果匹配,则出数据,直到不匹配或栈为空
b.如果不匹配,则继续入数据,直到匹配
3.结束标志:入栈序列走完了
代码实现:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
// write code here
int pushi = 0, popi = 0;
stack<int> st;
while(pushi < pushV.size())
{
st.push(pushV[pushi]);//st.push(pushV[pushi++]);下面的++pushi就不写了
//栈不为空且栈顶元素和出栈序列匹配
while(!st.empty()&&st.top() == popV[popi])
{
st.pop();
++popi;
}
++pushi;
}
return st.empty();
}150. 逆波兰表达式求值 - 力扣(LeetCode) 后缀表达式

理解题意:
eg1:
中缀表达式:a + b * (c - d)
改成后缀表达式: abcd - * +
eg2:
中缀表达式:a + b * c - d
后缀表达式:abc * + d -
巧妙解法:操作数按顺序排列,再看中缀,每当遇见操作符就往前看操作数根据符号优先级能否直接运算,能,则填入运算符,不能则获取下一个操作数,再看前面已经有的操作数和已有的运算符能否计算。比如现将abcd写出,再看中缀,发现a + b不能直接运算,继续往下看,录入*,不能运算,再录入c ,b*c符合逻辑,写上a(bc*),前面的+,也可以运算,写上(a(bc*)+)继续往下看 ,只有-d,于是:(a(bc*)+)d-写出,去掉括号,abc*+d-
解题思路:
题目是给出后缀表达式,实际上我们可以按照就近(一个符号和两个值就可以组成一次运算,先取出来的值是右操作数,后取到的值是)倒推,比如说:
ab*c/d+ <--->((a*b)/c)+d <-->ab*c/d+
两个值加一个符号就能组成一次运算,得到一个运算结果,相当于一个新值,再获取一个值一个符号这样的顺序。
1.依次将对象中的字符入栈,遇到操作符就出栈,依次为右操作数和左操作数,再将运算结果入栈将成为下一个运算的左操作数。
2.最后一个在栈中得数就是总运算结果。
方法一:暴力解法
class Solution { public: int evalRPN(vector<string>& tokens) { stack<int> s; for (size_t i = 0; i < tokens.size(); ++i) { string& str = tokens[i]; // str为数字 if (!("+" == str || "-" == str || "*" == str || "/" == str)) { s.push(atoi(str.c_str())); } else { // str为操作符 int right = s.top(); s.pop(); int left = s.top(); s.pop(); switch (str[0]) { case '+': s.push(left + right); break; case '-': s.push(left - right); break; case '*': s.push(left * right); break; case '/': // 题目说明了不存在除数为0的情况 s.push(left / right); break; } } } return s.top(); } };
方法二:用set(底层是搜索树)来解

1. 快速判断运算符
核心目的:将运算符集合 (
+,-,*,/) 存储在一个set中,用于快速检查当前字符串是否为运算符。这里考虑到的是如果在符号很多的情况下,优先使用set能便于快速查找。实现方式:
if (s.find(str) != s.end()) { // 判断 str 是否在集合 s 中 // 执行运算符操作 } else { // 处理操作数 }2. 性能分析
时间复杂度:
set的查找操作find()的时间复杂度为 O(log n),其中n是集合大小(此处n=4,实际几乎可以视为常数时间)。对比线性查找:对于少量元素(如4个运算符),
set的查找效率与逐个条件判断 (str == "+" || ...) 差异不大,但代码更简洁。
set在这段代码中充当了一个运算符过滤器,通过预定义的运算符集合,高效区分当前 token 是操作符还是操作数。这种设计在代码简洁性和可维护性之间取得了平衡,尤其适合需要灵活扩展运算符的场景。代码实现:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
//initializer_list构造函数
set<string> s = {"+","-","*","/"};
for(auto str : tokens)
{
//1.操作数入栈,操作符运算
if(s.find(str) != s.end())
{
//操作符
int right = st.top();
st.pop();
int left = st.top();
st.pop();
switch(str[0])//case必须是整型(char也是整型)
{
case '+':
st.push(left + right);
break;
case '-':
st.push(left - right);
break;
case '*':
st.push(left * right);
break;
case '/':
st.push(left / right);
break;
}
}
else
{
//没有找到操作符,就入栈
st.push(stoi(str));//string转化为int类型
}
}
return st.top();
}
};224. 基本计算器 - 力扣(LeetCode)(给一个中缀计算结果)拓展题目
解题思路:中缀转后缀
1.操作数输出
2.操作符入栈:
a、栈为空,入栈
b、比栈顶的运算符优先级高,就先入栈
c、比栈顶的运算符优先级低,出栈顶运算符
d、优先级相等,前一个可以先运算,出栈顶运算符
结束后将栈中操作符全部出栈。
转成后缀。
只要遇到左括号就递归,遇到右括号结束。(递归时会建立新栈,新的一轮优先级的比较)。
代码:省略;
三、队列
3.1 创建队列对象
#include <queue>
// 创建整型队列
queue<int> myQueue;
// 使用其他容器作为底层实现
queue<string, list<string>> listBasedQueue;3.2 六大核心方法
-
入队操作
myQueue.push(42);
myQueue.emplace("Hello"); // C++11高效构造-
访问元素
cout << "队首元素: " << myQueue.front();
cout << "队尾元素: " << myQueue.back(); // 注意:非标准队列可能不支持-
出队操作
myQueue.pop(); // 删除队首元素-
容量查询
if (!myQueue.empty()) {
cout << "当前元素数量: " << myQueue.size();
}队列的三大典型应用场景
3.3 消息队列实现
class MessageQueue {
private:
queue<string> messages;
mutex mtx;
public:
void addMessage(const string& msg) {
lock_guard<mutex> lock(mtx);
messages.push(msg);
}
string getMessage() {
lock_guard<mutex> lock(mtx);
if (messages.empty()) return "";
string msg = messages.front();
messages.pop();
return msg;
}
};应用场景:多线程通信、事件处理系统
3.4 广度优先搜索(BFS)
void BFS(vector<vector<int>>& graph, int start) {
vector<bool> visited(graph.size(), false);
queue<int> q;
q.push(start);
visited[start] = true;
while (!q.empty()) {
int current = q.front();
q.pop();
// 处理当前节点
cout << "访问节点: " << current << endl;
for (int neighbor : graph[current]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor);
}
}
}
}应用场景:社交网络关系分析、路径规划
3.5 实时数据缓冲
class DataBuffer {
queue<SensorData> buffer;
const int MAX_SIZE = 100;
public:
void addData(const SensorData& data) {
if (buffer.size() >= MAX_SIZE) {
buffer.pop(); // 移除最旧数据
}
buffer.push(data);
}
void processBatch() {
while (!buffer.empty()) {
process(buffer.front());
buffer.pop();
}
}
};应用场景:物联网传感器数据处理、音视频流缓冲
栈的模拟实现:
#pragma once
#include<vector>
#include<list>
namespace bit
{
//写法一
//template<class T>
//class stack
//{
//public:
//private:
// //1.数组
// T* _a;
// //2.top
// int _top;
// //3.容量
// int _capacity;
//};
// 写法二:
//设计模式:适配器模式 -- 转换
//我们可以用vector、list来实现栈,因此也可以做一个容器模版,我们不会知道我们的栈是数组栈还是链表栈
//泛型编程
//stack<int, vector<int>> st1
//stack<int, list<int>> st2
template<class T, class Container>
class stack
{
public:
//1 2 3 4 5
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
const T& top()
{
return _con.back();
}
private:
Container _con;
};测试代码:
void test_stack1()
{
bit::stack<int, vector<int>> st;
st.push(1);
st.push(2);
st.push(3);
st.push(4);
while (!st.empty())
{
cout << st.top() << " ";
st.pop();
}
cout << endl;
}
int main()
{
test_stack1();
}在我们实际应用时,stack的第二个参数是可以不传的,因此我们的模拟代码还需要修改。
我们的模版参数和函数参数相似,模版参数传的是类型,函数参数传的是对象,函数参数可以有缺省参数,模版参数也可以有缺省参数,从右往左缺省。
如图:写一个默认参数

队列的模拟实现:
和栈的模拟实现类似,有一些区别,因为队列是先进先出,因此在pop()时,应该pop_front();
以及在库中对于队列模版参数默认值是传的deque(双端队列),不是真队列(不要求先进先出)


deque是一个很牛的容器
vector
优点:支持下标随机访问
缺点:头部或者中间插入的效率低,扩容有消耗
list
优点:任意位置插入删除效率都不错
缺点:不支持下表随机访问
但如上图:我们可以发现,deque就是vector和list的合体
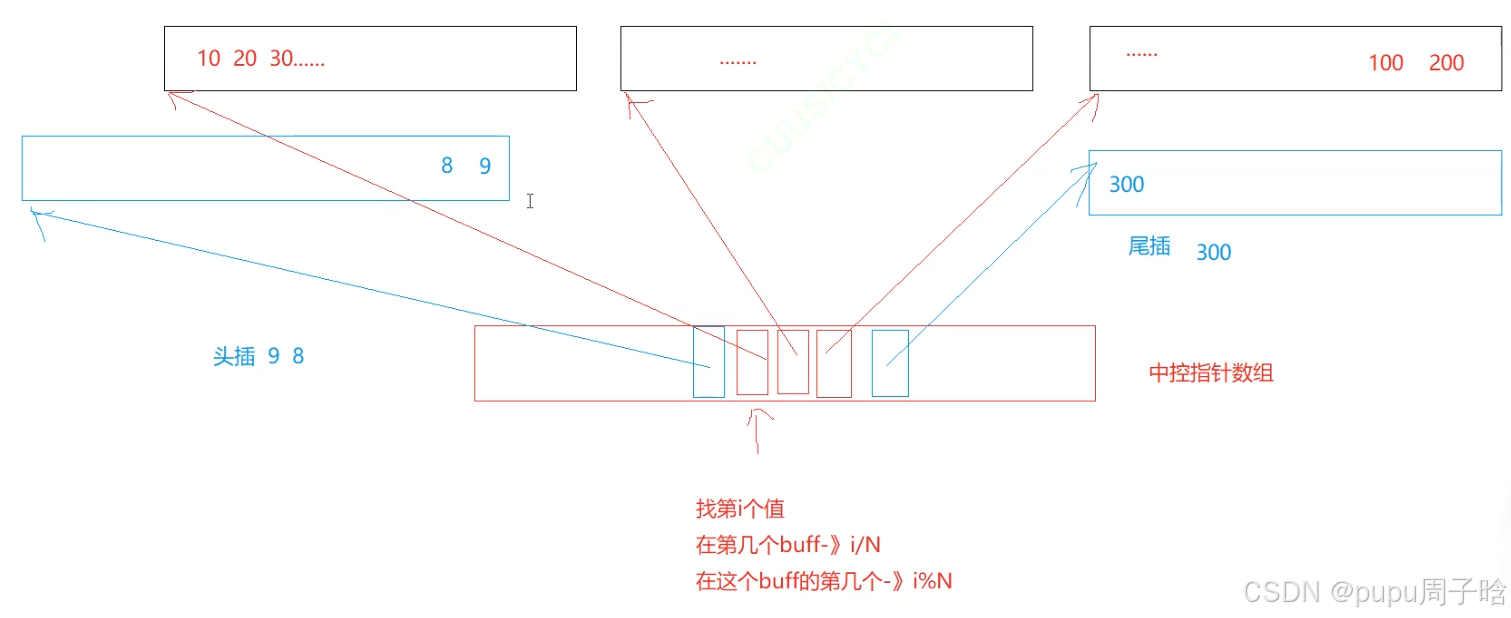
deque实现思想:
1.开多个小数组
2.中控指针数组 指针从中间往两边放,存小数组地址
尾差:最后一个buffer没满,就插入这个buffer里面,如果满了就新开一个buffer,在中控指针数组内再往后添加一个指针,指向新的数组地址
头插: 在中控指针数组内再往前添加一个指针指向新数组空间,在新的数组空间内头插(请注意:指针存的是数组地址,存入数据是从数组尾部开始存入)
中控数组满:扩容(类似于vector扩容的方式)
扩容后,要找第i个值需要做两个判断:
1.如果第一个buffer不满: i -= 第一个buffer的数据个数。
( 如果是满的,就不用i -= 第一个buffer的数据个数。)
2.再算在第几个buffer里面:buff -> i/N;在这个buffer内的第几个? i%N
总图:

deque优缺点
优点:头插尾插的效率都很好。比顺序表和链表都要好一些
缺点:
1.中间插入删除会比较麻烦,效率一般。a.整体移动,b.局部移动
2.[]效率不够极致
为什么栈和队列的默认容器都是deque?因为deque的头尾插的效率很好。
队列的模拟实现代码:
#pragma once
#include<deque>
#include<list>
namespace bit
{
template<class T, class Container = deque<T>>
class Queue
{
public:
//1 2 3 4 5
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front(); //注意在队头出
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
const T& front()
{
return _con.front();
}
const T& back()
{
return _con.back();
}
private:
Container _con;
};
}结语:
随着这篇关于题目解析的博客接近尾声,我衷心希望我所分享的内容能为你带来一些启发和帮助。学习和理解的过程往往充满挑战,但正是这些挑战让我们不断成长和进步。我在准备这篇文章时,也深刻体会到了学习与分享的乐趣。
在此,我要特别感谢每一位阅读到这里的你。是你的关注和支持,给予了我持续写作和分享的动力。我深知,无论我在某个领域有多少见解,都离不开大家的鼓励与指正。因此,如果你在阅读过程中有任何疑问、建议或是发现了文章中的不足之处,都欢迎你慷慨赐教。
你的每一条反馈都是我前进路上的宝贵财富。同时,我也非常期待能够得到你的点赞、收藏,关注,这将是对我莫大的支持和鼓励。当然,我更期待的是能够持续为你带来有价值的内容,让我们在知识的道路上共同前行。