【算法训练营Day31】单调栈

单调栈理论基础

单调栈是一种 特殊的栈数据结构，核心特点是 栈内元素始终保持严格的单调性（单调递增或单调递减）。它的核心价值是：用 O(n) 时间复杂度 解决“找数组中每个元素的前后第一个比它大/小的元素”这类问题——这类问题暴力解法是 O(n²)，单调栈通过“维护栈的单调性”实现一次遍历完成求解。

一、单调栈的核心定义与作用

1. 定义

• 栈内元素遵循 “单调递增”或“单调递减” 规则（可分为“严格单调”和“非严格单调”，根据题目需求选择）。
• 是“辅助栈”：不直接存储最终结果，而是通过维护单调性，快速定位目标元素的位置关系。

2. 核心作用

解决以下两类高频问题（本质是“元素的位置关系查找”）：

• 找数组中 每个元素的下一个更大元素（右边第一个比它大的）；
• 找数组中 每个元素的下一个更小元素（右边第一个比它小的）；
• 衍生问题：找前一个更大/更小元素、计算元素间距离、接雨水、最大矩形等。

二、单调栈的核心性质

1. 单调性：栈内元素要么“从小到大”（单调递增栈），要么“从大到小”（单调递减栈）。单调栈的 “递增 / 递减” 是 栈底到栈顶 的顺序。

   • 单调递增栈：栈顶是最大元素，栈底是最小元素（新元素入栈时，弹出所有比它大的元素，再入栈）；
   • 单调递减栈：栈顶是最小元素，栈底是最大元素（新元素入栈时，弹出所有比它小的元素，再入栈）。

2. 栈内元素的意义：栈中存储的是 数组元素的索引（而非元素值本身），通过索引可快速获取元素值和位置，方便计算距离。

3. 操作原则（核心！）：
   遍历数组时，对于当前元素 nums[i]，破坏栈单调性的元素会被弹出，直到栈满足单调性为止，再将当前索引 i 入栈。

   • 弹出栈顶元素时，当前元素 nums[i] 就是“栈顶元素的目标元素”（如下一个更大/更小元素）。

三、单调栈的基本操作步骤
以“找每个元素的下一个更大元素”为例（用单调递减栈），步骤如下：

1. 初始化：创建空栈（存索引），创建结果数组 res（长度与原数组一致，默认值如 -1）；
2. 遍历数组：从左到右遍历每个元素 nums[i]；
3. 维护栈单调性：
   • 若栈不为空，且 nums[i] > nums[栈顶索引]（破坏单调递减），则弹出栈顶索引 top；
   • 弹出后，nums[i] 就是 nums[top] 的“下一个更大元素”，将 res[top] = nums[i]（或存索引/距离）；
   • 重复上两步，直到栈为空或 nums[i] ≤ nums[栈顶索引]（满足单调性）；
4. 入栈当前索引：将 i 入栈，维持栈的单调性；
5. 遍历结束：栈中剩余索引的目标元素不存在（如 res 中仍为 -1）。

总结
单调栈的核心逻辑是 “用单调性换效率”——通过维护栈内元素的有序性，让每个元素“入栈一次、出栈一次”，实现 O(n) 时间复杂度。

做题时的快速判断：

• 看到“找前后第一个比当前大/小的元素”→ 单调栈；
• 看到“柱状图、接雨水、最大矩形”→ 单调栈（递增/递减根据场景选）。

每日温度

题目链接：739. 每日温度

解题思路：

利用单调递减栈，即可解决问题

解题代码：

class Solution {public int[] dailyTemperatures(int[] temperatures) {//单调递减栈int[] result = new int[temperatures.length];Deque<Integer> stack = new ArrayDeque<>();for(int i = 0;i < temperatures.length;i++) {while(!stack.isEmpty() && temperatures[stack.peek()] < temperatures[i]) {int index = stack.pop();result[index] = i - index;}stack.push(i);}return result;}
}

下一个更大元素 I

题目链接：下一个更大元素 I

解题逻辑：

同样使用单调递减栈

解题代码：

class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {//使用单调递减栈int[] result = new int[nums1.length];Map<Integer,Integer> map = new HashMap<>();Deque<Integer> stack = new ArrayDeque<>();for(int i = 0;i < nums1.length;i++) map.put(nums1[i],i);for(int i = 0;i < nums2.length;i++) {while(!stack.isEmpty() && nums2[stack.peek()] < nums2[i]) {int index = stack.pop();if(map.containsKey(nums2[index])) result[map.get(nums2[index])] = nums2[i];}stack.push(i);}for(int i = 0;i < result.length;i++) if(result[i] == 0) result[i] = -1;return result;}
}

下一个更大元素II

题目链接：503. 下一个更大元素 II

方法一：取模 + 暴力

看到循环数组很自然的可以想到用取模的方式获取数，代码如下：

class Solution {public int[] nextGreaterElements(int[] nums) {int[] result = new int[nums.length];for(int i = 0;i < nums.length;i++) {boolean flag = true;for(int j = 1;j < nums.length;j++) {int next = (i + j) % nums.length;if(nums[next] > nums[i]) {result[i] = nums[next];flag = false;break;}}if(flag) result[i] = -1;}return result;}
}

方法二：取模 + 单调栈

既然是循环数组，那么找到所有的下一个更大元素最多只需要两个循环。其他的逻辑和方法一差不多。

class Solution {public int[] nextGreaterElements(int[] nums) {//仍然使用递减单调栈int[] result = new int[nums.length];boolean[] record = new boolean[nums.length];Deque<Integer> stack = new ArrayDeque<>();for(int i = 0;i < nums.length * 2;i++) {while(!stack.isEmpty() && nums[stack.peek()] < nums[i % nums.length]) {int index = stack.pop();result[index] = nums[i % nums.length];record[index] = true;}stack.push(i % nums.length);}for(int i = 0;i < result.length;i++) if(!record[i]) result[i] = -1;return result;}
}

接雨水

题目链接：42. 接雨水

先前我们使用双指针做过一次，其整体是一种纵向求解。

而如果使用单调栈来求解的话，其本质是一种横向求解。

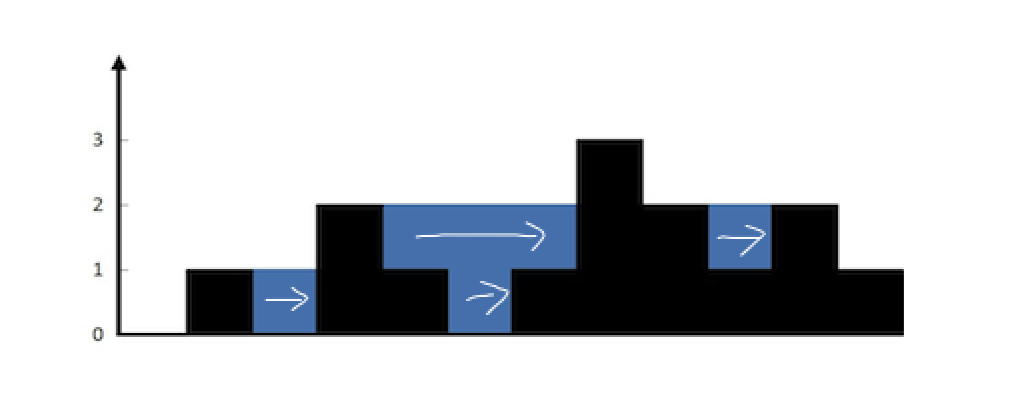
而如果想要横向求解，那么有三个要素是必须要知道的：

• 左边界（栈顶元素）
• 右边界（当前遍历的元素）
• 下边界（要弹出栈的元素）

知道这三个元素之后，每次计算相应的横向面积然后叠加即可：

class Solution {public int trap(int[] height) {//使用递减单调栈int result = 0;Deque<Integer> stack = new ArrayDeque<>();for(int i = 0;i < height.length;i++) {while(!stack.isEmpty() && height[stack.peek()] < height[i]) {int middle = height[stack.pop()];int left = height[i];if(stack.isEmpty()) break;int right = height[stack.peek()];result += (Math.min(left,right) - middle) * (i - stack.peek() - 1);}stack.push(i);}return result;}
}

最小栈

题目链接：155. 最小栈

方法一：单独维护一个min变量，用来表示栈中的最小值

class MinStack {Deque<Integer> stack = new ArrayDeque<>();int min = Integer.MAX_VALUE;public MinStack() {}public void push(int val) {stack.push(val);if(val <= min) min = val;}public void pop() {stack.pop();if(!stack.isEmpty()) min = stack.stream().mapToInt(Integer::intValue).min().getAsInt();else min = Integer.MAX_VALUE;}public int top() {return stack.peek();}public int getMin() {return min;}
}

方法二：双栈法

一个栈用来存储元素，一个栈用来维护最小元素。

这个方法为什么可行？两个栈的一致性是怎么实现的？

• 我们在进行压栈操作的时候，最小数栈也只会根据情况压栈，不会出现弹出的情况，所以最小栈中的元素相对顺序和主栈中是一样的。
• 而主栈弹栈的时候，最小栈栈顶有就弹，没有就不谈，相对顺序并没有被破环。

class MinStack {Deque<Integer> stack = new ArrayDeque<>();Deque<Integer> min = new ArrayDeque<>();public MinStack() {}public void push(int val) {stack.push(val);if(min.isEmpty() || (!min.isEmpty() && min.peek() >= val)) min.push(val);}public void pop() {int val = stack.pop();if(!min.isEmpty() && min.peek() == val) min.pop(); }public int top() {return stack.peek();}public int getMin() {return min.peek();}
}

字符串解码

题目链接：394. 字符串解码

解题逻辑：

本题就是典型的栈的括号匹配，在此基础上加上了“一点点”代码操控能力的考察

注意点：一段内容入栈之后再弹出来顺序是反着的，需要注意处理

解题代码：

class Solution {public String decodeString(String s) {StringBuilder str = new StringBuilder();Deque<Character> stack = new ArrayDeque<>();for(char c : s.toCharArray()) {if(c != ']') stack.push(c);else {StringBuilder word = new StringBuilder();StringBuilder count = new StringBuilder();while(!stack.isEmpty() && stack.peek() != '[') word.append(stack.pop());stack.pop();while(!stack.isEmpty() && stack.peek() != '[' && stack.peek() != ']' && Character.isDigit(stack.peek())) count.append(stack.pop());int countInt = Integer.parseInt(count.reverse().toString());word = word.reverse();StringBuilder temp = new StringBuilder();for(int i = 0;i < countInt;i++) temp.append(word);if(stack.isEmpty()) str.append(temp);else for (char c1 : temp.toString().toCharArray()) stack.push(c1);}}StringBuilder temp = new StringBuilder();while(!stack.isEmpty()) temp.append(stack.pop());str.append(temp.reverse());return str.toString();}
}

柱状图中最大的矩形

题目链接：84. 柱状图中最大的矩形

方法1：暴力枚举

这个方法会超过时间限制，但是这种解决方法我们要能想到，暴力法在面试环境中也不失为一种解决办法：

class Solution {public int largestRectangleArea(int[] heights) {int max = 0;for(int i = 0;i < heights.length;i++) {int h = heights[i];if(h > max) max = h;for(int j = i - 1;j >= 0;j--) {if(heights[j] < h) h = heights[j];int area = h * (i - j + 1);if(area > max) max = area;}}return max;}
}

方法2：单调栈

寻找以第i根柱子为最矮柱子所能延伸的最大面积，那么我们的目标就变为了寻找左边第一个小于该柱子的位置，以及右边第一个小于该柱子的位置。

本题要使用递增单调栈：

class Solution {public int largestRectangleArea(int[] heights) {int max = 0;Deque<Integer> stack = new ArrayDeque<>();for(int i = 0;i < heights.length;i++) {while(!stack.isEmpty() && heights[stack.peek()] > heights[i]) {int middle = stack.pop();int area;if(!stack.isEmpty()) {area = heights[middle] * (i - stack.peek() - 1);}else {area = heights[middle] * i;}if(area > max) max = area;}stack.push(i);}while(!stack.isEmpty()) {int middle = stack.pop();int area;if(!stack.isEmpty()) {area = heights[middle] * (heights.length - stack.peek() - 1);}else {area = heights[middle] * heights.length;}if(area > max) max = area;}return max;}
}

总结：对单调栈的进一步理解

单调栈解决的问题：找数组中每个元素的前后第一个比它大/小的元素！！！

例如：

• 单调递减栈：用于查找数组中每个元素的前后第一个比它大的元素
• 单调递增栈：用于查找数组中每个元素的前后第一个比它小的元素

搞清楚这个场景中三个最基本的要素（以单调递减栈为例）：

• 当前元素是此时栈顶的元素
• 该元素的前面第一个比它大的元素就是栈顶的下一个元素，如果没有说明该元素前面没有比它大的
• 该元素的后面第一个比它大的元素就是当前遍历的元素。如果最后单调栈中仍有元素，说明这些元素的后面没有比他大的元素。

基本模板：

		Deque<Integer> stack = new ArrayDeque<>();for(int i = 0;i < heights.length;i++) {//此处是单调递增栈，如果是单调递减栈则heights[stack.peek()] < heights[i]while(!stack.isEmpty() && heights[stack.peek()] > heights[i]) {//根据单调栈的三个基本要素书写逻辑}stack.push(i);}