2022年IEEE TITS SCI2区TOP,基于切线交点和目标引导策略的无人机自主路径规划,深度解析+性能实测
目录
- 1.摘要
- 2.问题描述
- 3.APPATT算法
- 4.结果展示
- 5.参考文献
- 6.代码获取
- 7.算法辅导·应用定制·读者交流
1.摘要
无人机路径规划使无人机能够避开障碍物并高效到达目标,为了生成无障碍碰撞的高质量路径,本文提出了一种基于切线交点和目标引导策略的自主路径规划算法(APPATT)。在目标引导下,采用椭圆切线图方法生成两条子路径,当遇到障碍物时,基于启发式规则选择其中一条子路径。无人机沿选定的子路径飞行,并通过这种方式反复调整飞行路径,以避开障碍物,直到无碰撞路径延伸到目标。考虑到无人机的运动约束,采用三次B样条曲线平滑航点,以获得可行路径。
2.问题描述
在此场景中,假设无人机需从起点SSS飞往终点EEE,但高楼阻挡了直接路径,因此需要规划一条无碰撞的路径。为提高计算效率并简化路径搜索,三维环境被简化为二维场景。障碍物被统一建模为椭圆形,以避免不规则多边形带来的计算复杂性和路径不平滑问题。环境中有NNN个障碍物,每个障碍物的中心坐标为(xk,yk)(x_k, y_k)(xk,yk),半长轴和半短轴分别为aaa和bbb,倾斜角度为θ\thetaθ,rsafer_{safe}rsafe为无人机与障碍物之间的最小安全距离。
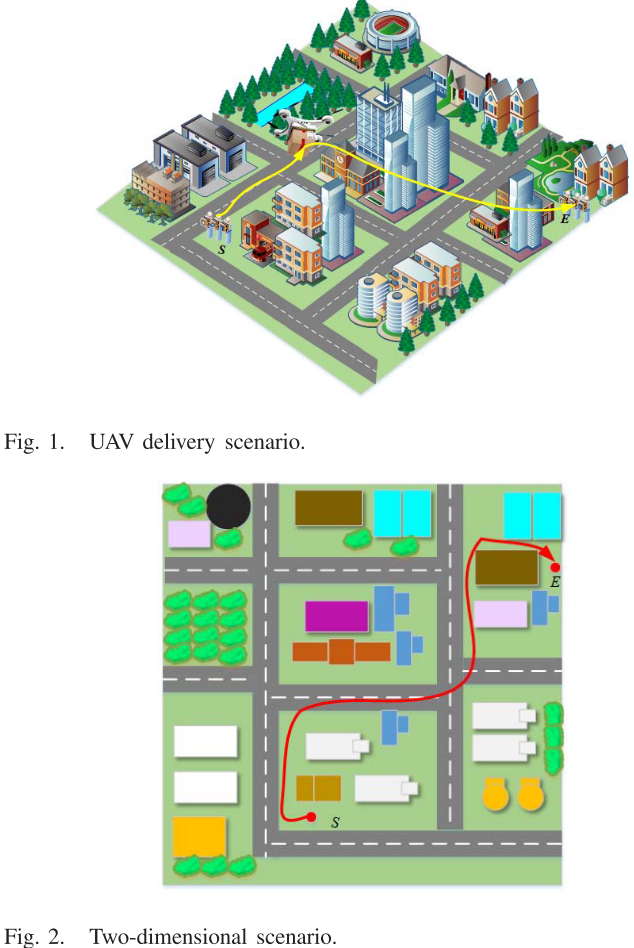
障碍物可以表示为:
[(x−xk)cosθ+(y−yk)sinθ]2(a+rsafe)2+[(y−yk)cosθ−(x−xk)sinθ]2(b+rsafe)2=1\begin{aligned} \frac{[(x-x_k)cos\theta+(y-y_k)sin\theta]^2}{(a+r_{safe})^2} +\frac{[(y-y_k)cos\theta-(x-x_k)sin\theta]^2}{(b+r_{safe})^2}=1 \end{aligned} (a+rsafe)2[(x−xk)cosθ+(y−yk)sinθ]2+(b+rsafe)2[(y−yk)cosθ−(x−xk)sinθ]2=1
无碰撞路径上的每个路点满足:
[(xi−xk)cosθ+(yi−yk)sinθ]2(a+rsafe)2+[(yi−yk)cosθ−(xi−xk)sinθ]2(b+rsafe)2≥1\begin{aligned} \frac{[(x_{i}-x_{k})cos\theta+(y_{i}-y_{k})sin\theta]^{2}}{(a+r_{safe})^{2}} +\frac{[(y_i-y_k)cos\theta-(x_i-x_k)sin\theta]^2}{(b+r_{safe})^2}\geq1 \end{aligned} (a+rsafe)2[(xi−xk)cosθ+(yi−yk)sinθ]2+(b+rsafe)2[(yi−yk)cosθ−(xi−xk)sinθ]2≥1
3.APPATT算法
APPATT通过在遇到障碍物时基于椭圆切线图生成两条子路径,并根据规则选择其中一条路径,避免构建整个道路图。算法分为两种版本:SETG-TG(已知环境)和DETG-TG(实时收集环境信息)。APPATT通过连接无碰撞的交点生成高质量路径,避免不必要的计算,并能根据障碍物位置动态调整路径。
SETG-TG算法
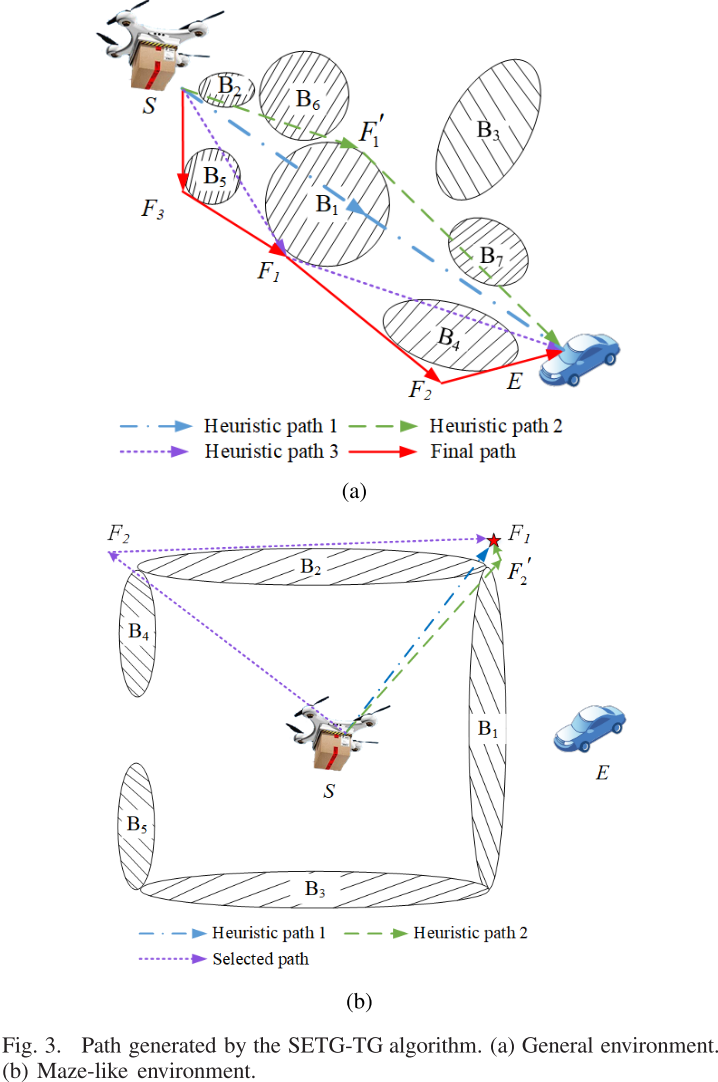
SETG-TG算法通过生成航点并更新起点和终点,迭代地寻找无碰撞路径。算法步骤包括: 使用椭圆建模障碍物; 初始化起点和终点并设置航点集合;判断从起点到终点的路径是否无碰撞,若有碰撞则生成切线并根据启发式规则选择路径。算法不断调整路径,直到找到一条无碰撞的路径到达终点,适用于已知环境下的路径规划。

DETG-TG算法
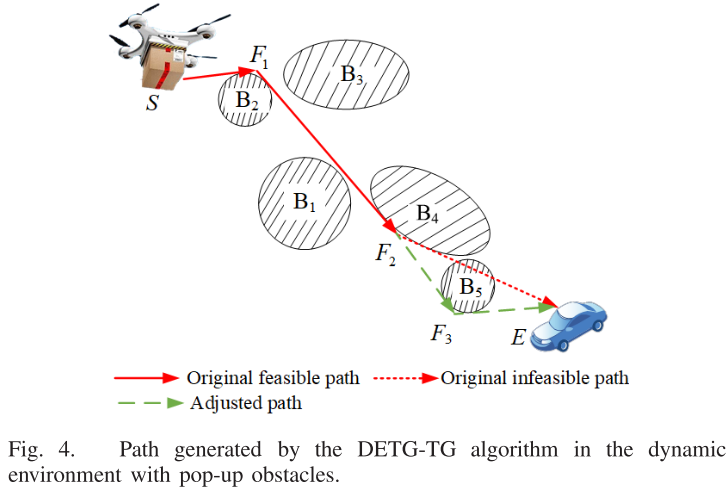
DETG-TG算法适用于动态环境和完全未知环境。在动态环境中,算法通过实时感知和重新规划碰撞路径应对突发障碍物;在未知环境中,算法通过传感器逐步感知并更新环境信息,限制飞行距离以频繁调整路径。算法通过迭代步骤,生成无碰撞路径并避开障碍,直至无人机到达终点。

4.结果展示
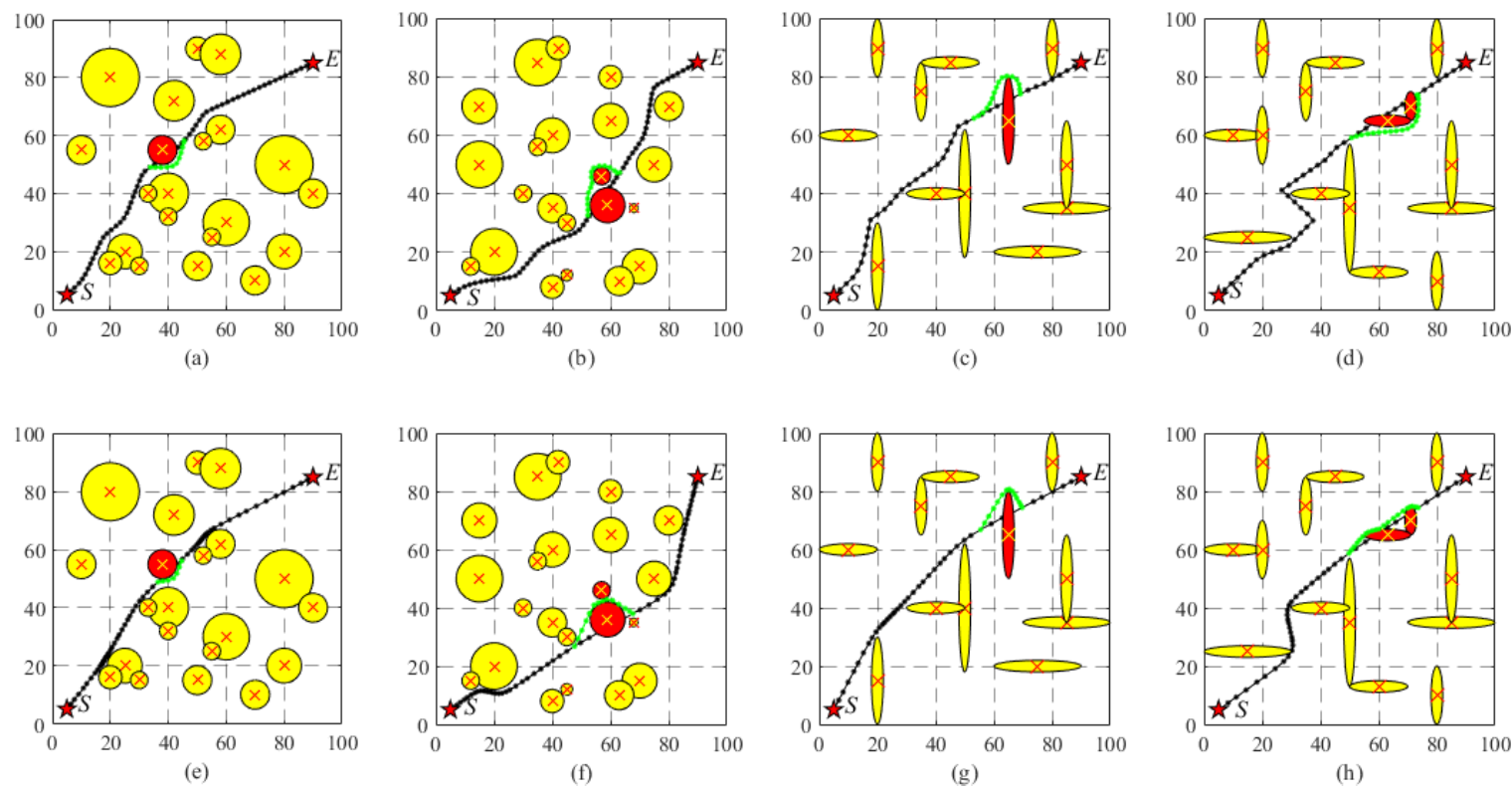
5.参考文献
[1] Liu H, Li X, Fan M, et al. An autonomous path planning method for unmanned aerial vehicle based on a tangent intersection and target guidance strategy[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 23(4): 3061-3073.
6.代码获取
xx
7.算法辅导·应用定制·读者交流
xx
