深度学习入门：基于Python的理论与实现（理论研究）

前言

学习建议：

一.机器学习的重要概念/基础知识

有监督学习，无监督学习，强化学习

https://www.cnblogs.com/zgx1227/p/19065594（监督学习VS无监督学习）

数学课程

微积分，线性代数，概率论，最优化方法

微积分

导数

导数的基本概念

求导公式

高阶导数

函数

相关概念

一元函数的极值判别法则

一元函数的泰勒展开

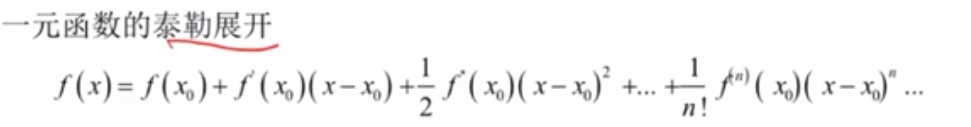
线性代数

向量

概念

内积：对应元素相乘再累加，向量变标量。

向量的范数

https://blog.csdn.net/m0_66201040/article/details/128710007（向量范数）

https://blog.csdn.net/Yangtze20/article/details/144120810（向量，矩阵范数）

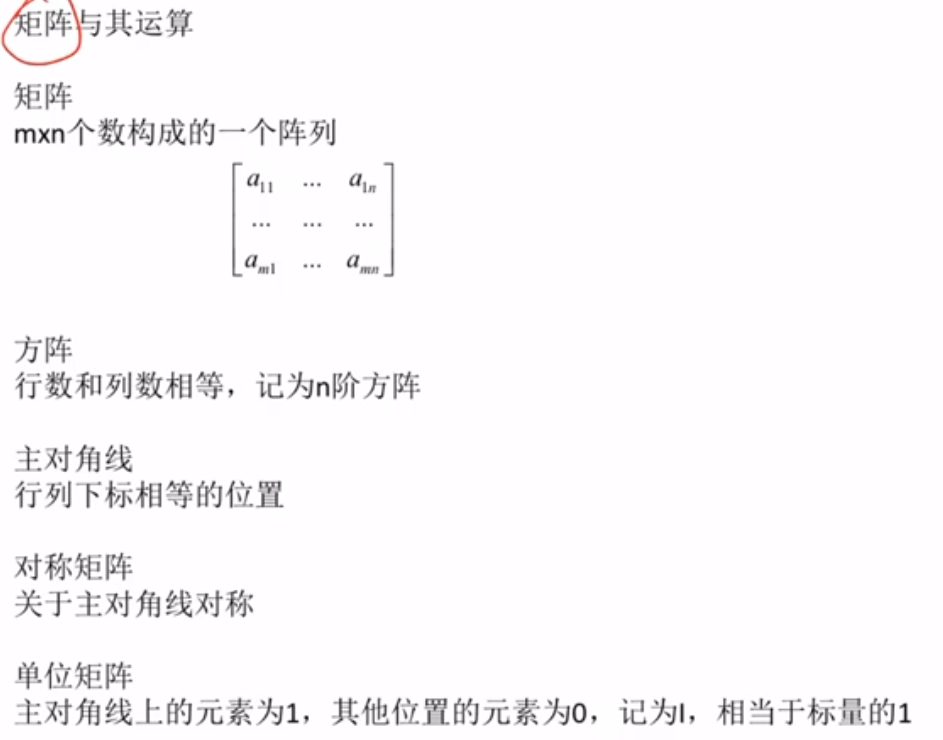
矩阵

概念

·

特征值与特征向量

I为齐次单位矩阵E

二次型

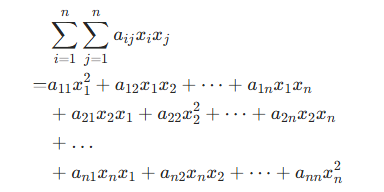
张量

偏导数

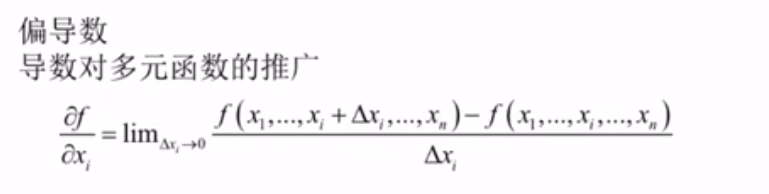
梯度（重要概念）

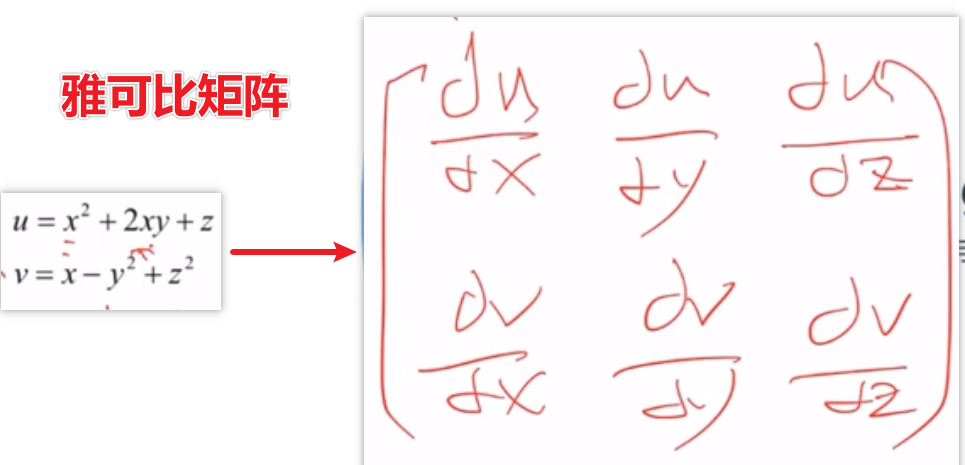
雅可比矩阵

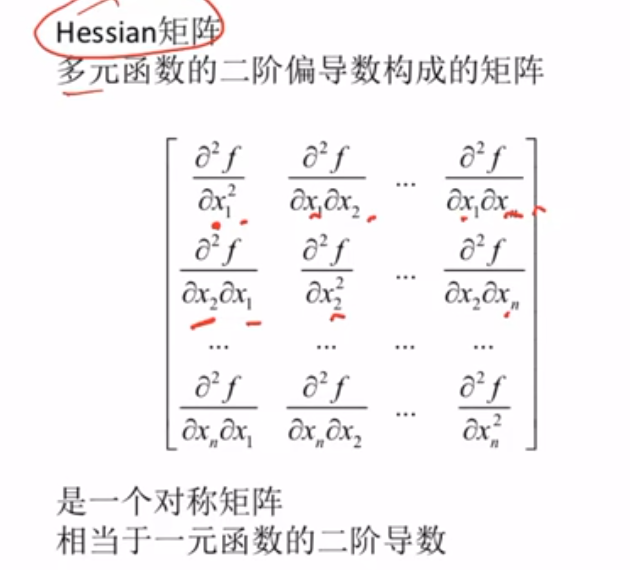
Hessian矩阵

多元函数的极值判别法则

多元函数的泰勒展开（这个地方不清楚）

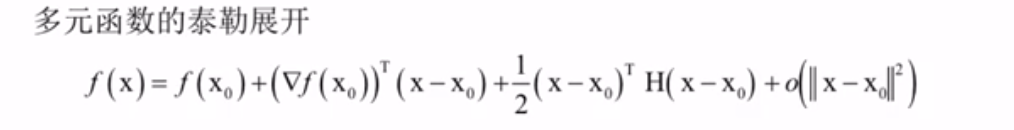
这是多元函数的泰勒展开式，用于将多元函数 f(x)在x0附近展开，是一元函数泰勒展开在高维空间的推广。

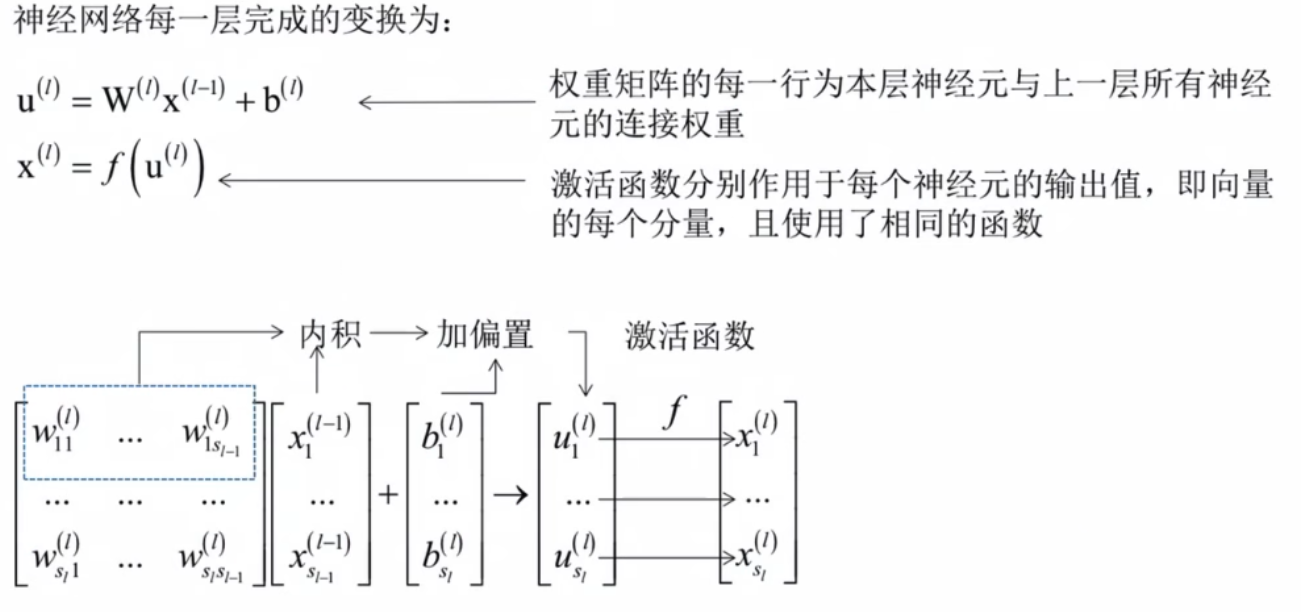
矩阵和向量求导（机器学习重要公式)

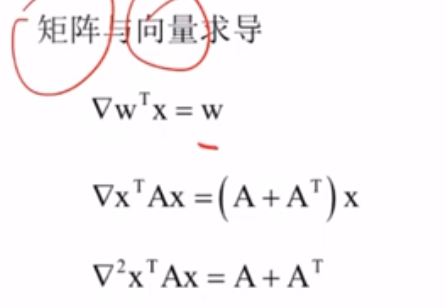
概率论

随机事件与概率(需补充）

条件概率与贝叶斯公式

随机事件的独立性

随机变量

二.人工神经网络ANN

神经元

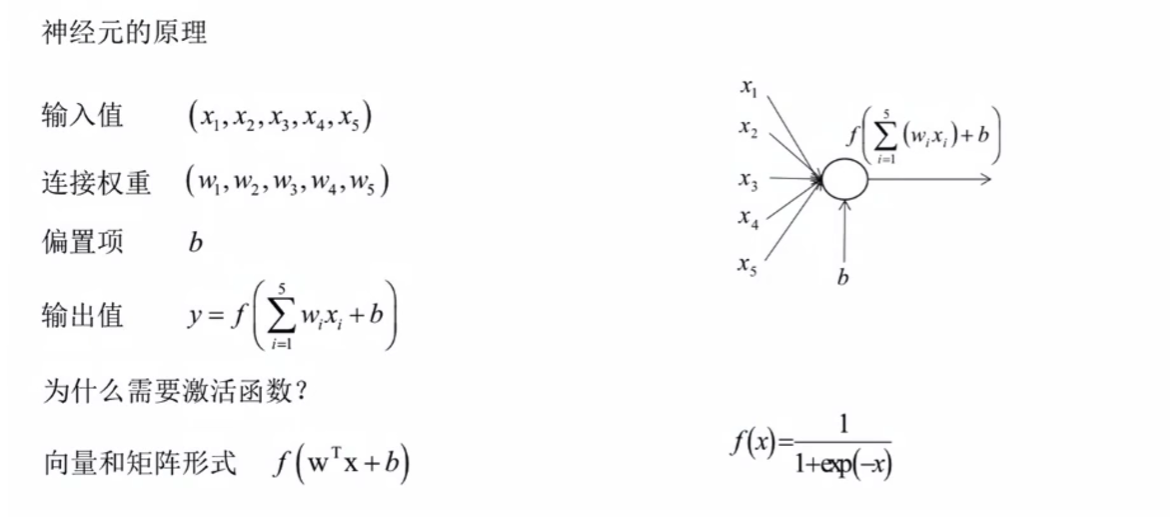
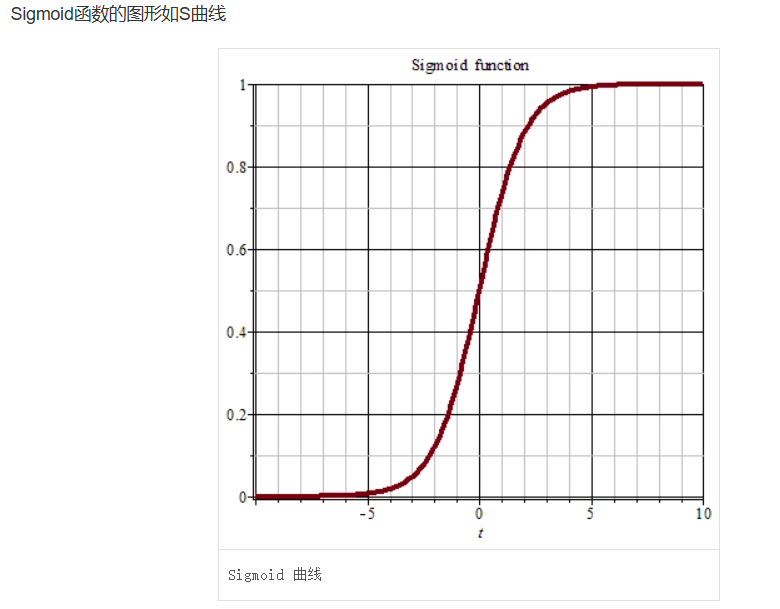
激活函数——Sigmoid函数

神经网络结构

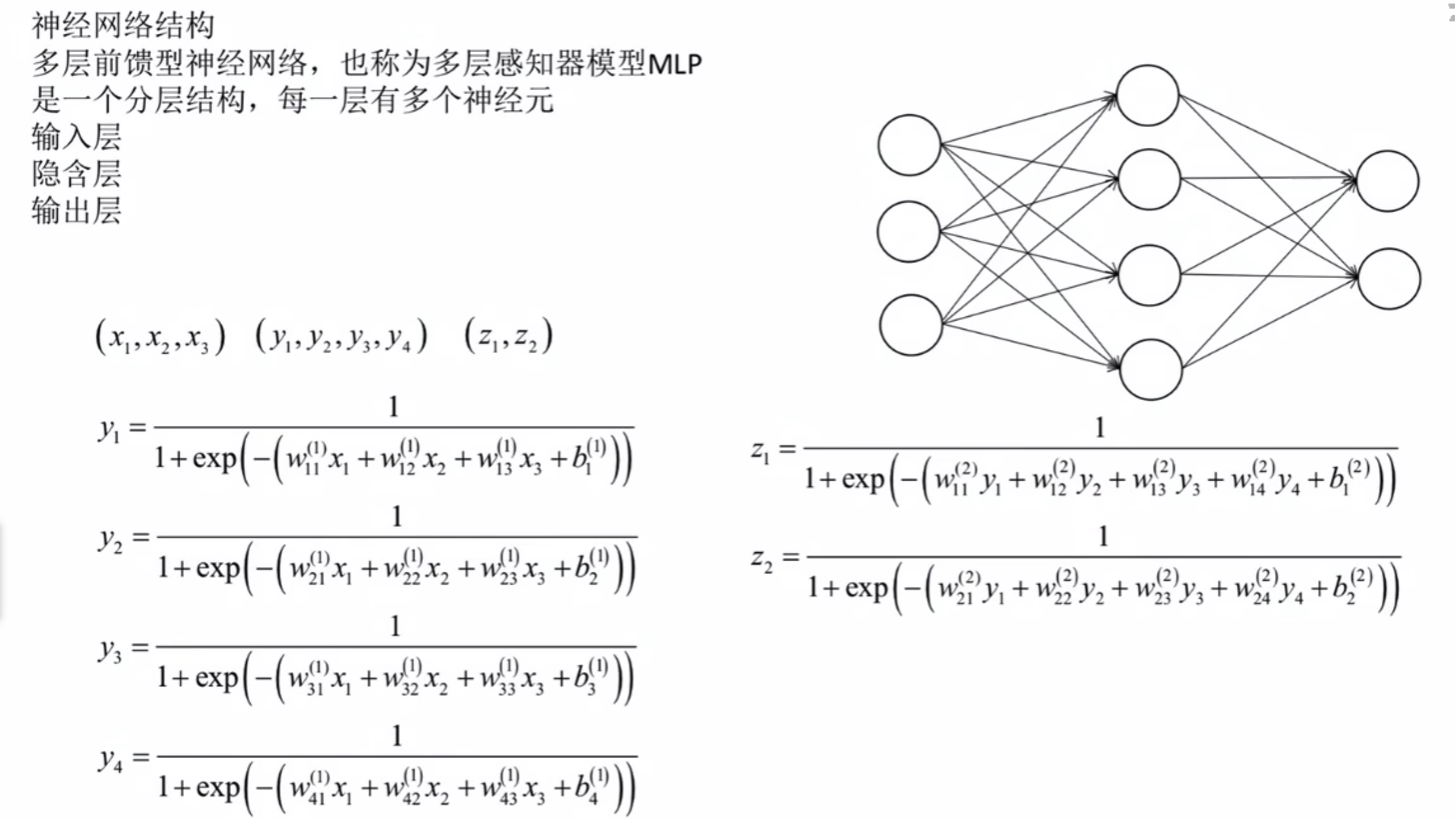
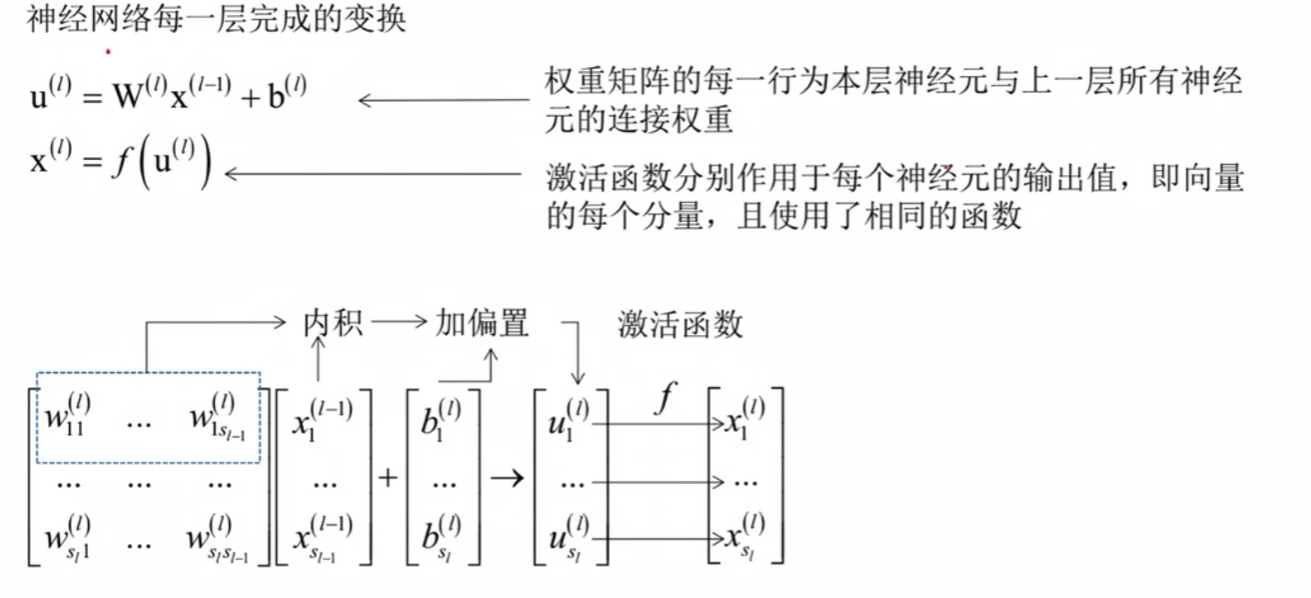
正向传播算法

分类问题

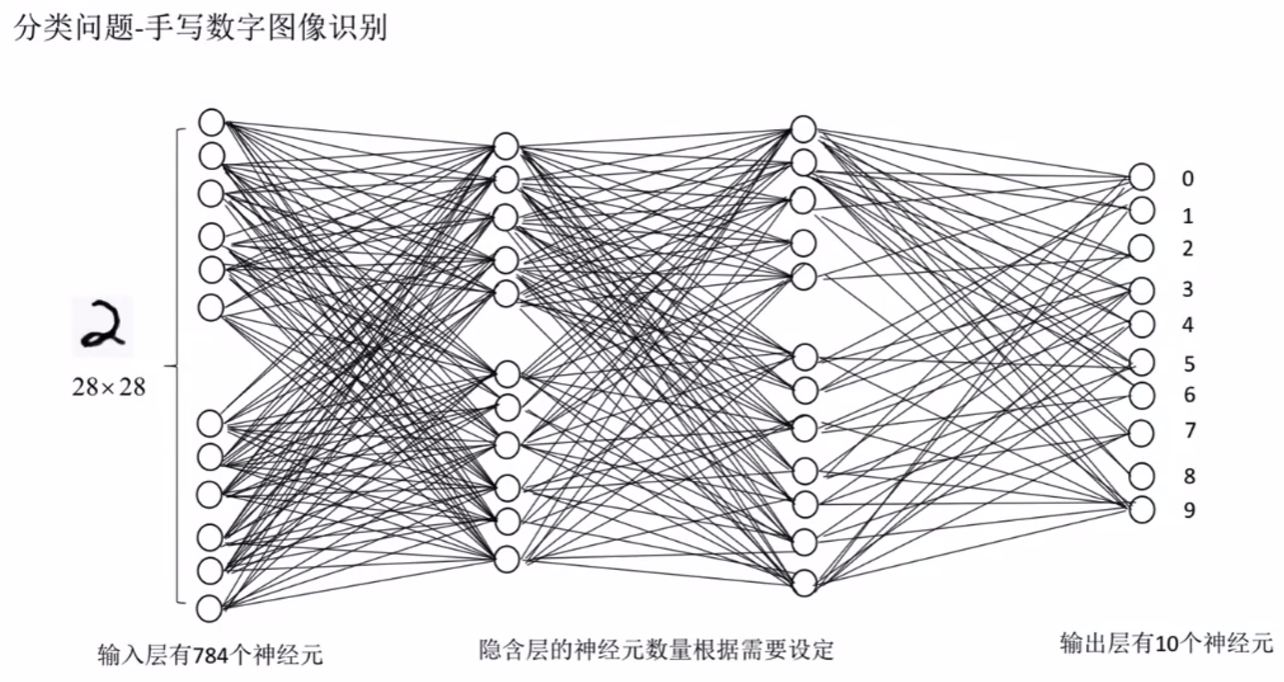
最后输出层2的数值最大，最终手写识别为2.

回归问题

反向传播算法

反向传播算法

经典论文

反向传播

Transformer架构

《Attention is all you need》

正向传播

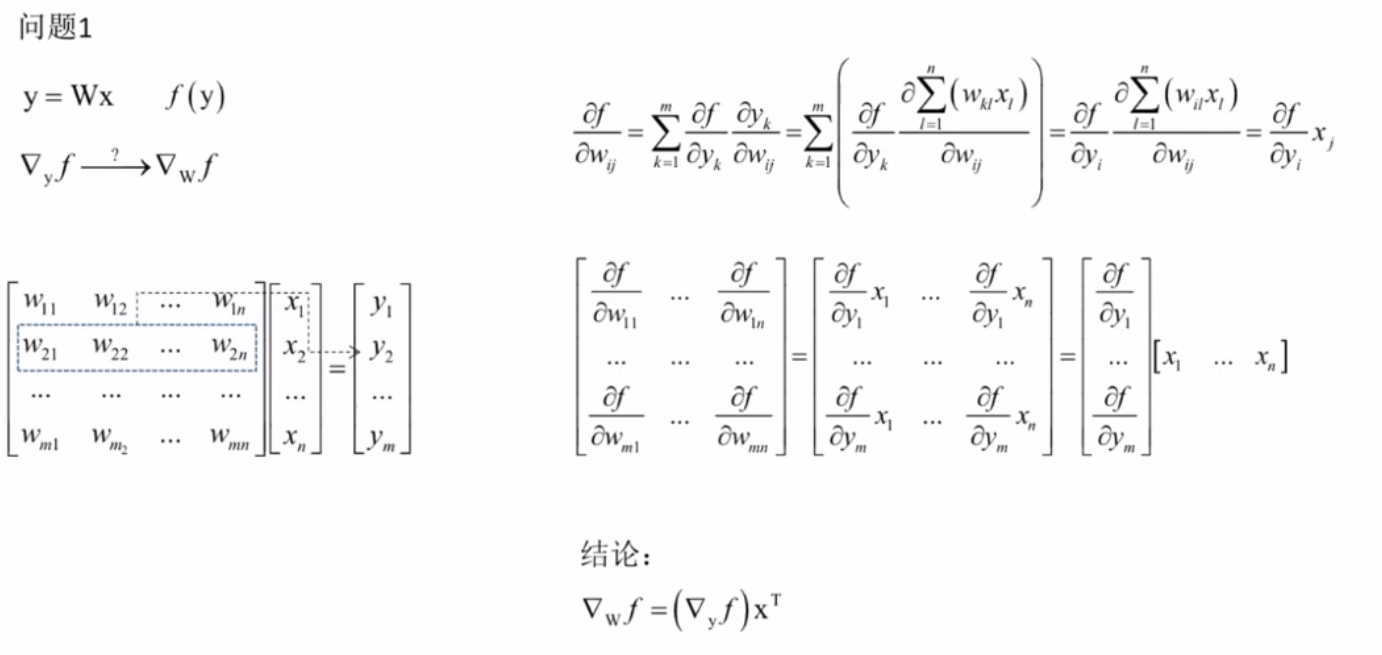
目标函数

欧氏距离损失函数的导数

链式法则

几个重要的求导公式

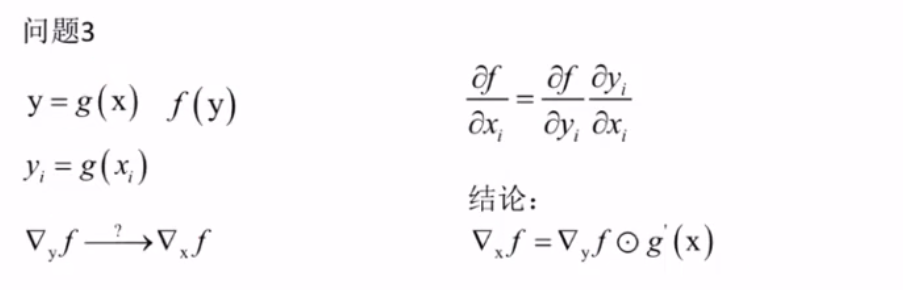
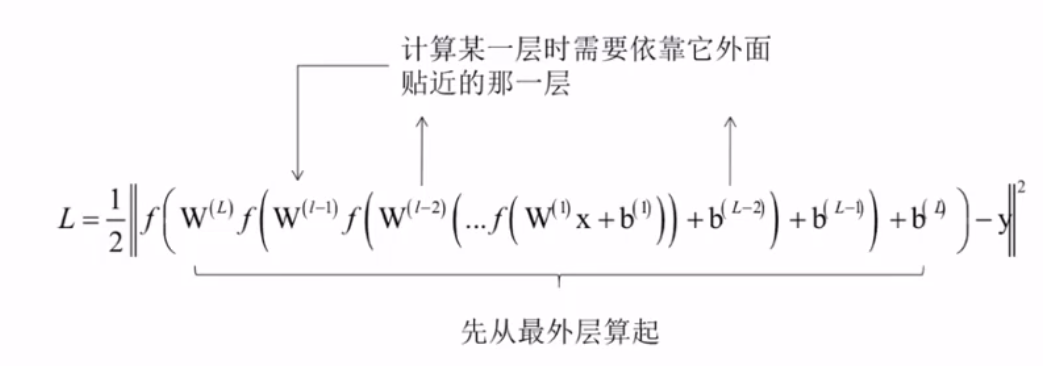
损失函数

计算权重和偏置的梯度

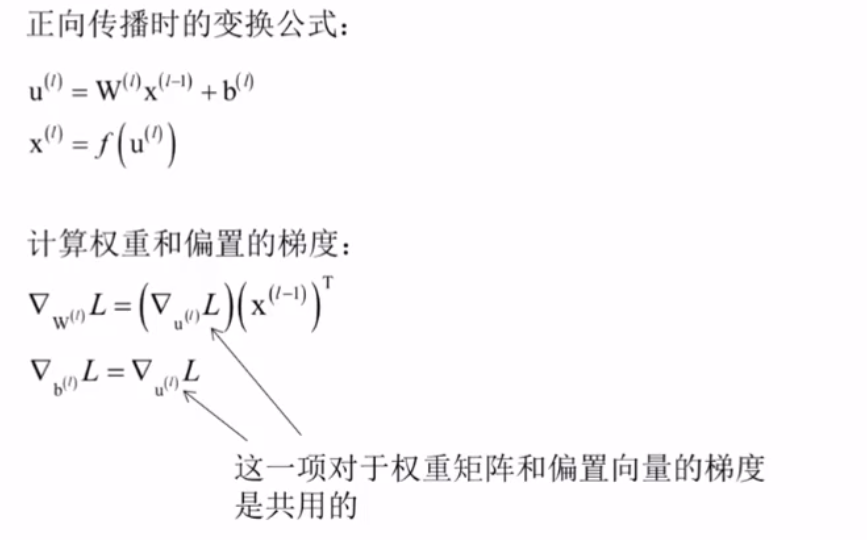
计算梯度的前一项是对前面几个重要的求导公式的具体运用，不清楚的话应该翻翻看问题1，2等。最后一项对b和对u的梯度为什么一样，不清楚。

计算临时变量的梯度

反向传播算法总结

工程实现问题

三.人工神经网络实现

实验关键环节

人工神经网络的数学特性——拟合能力

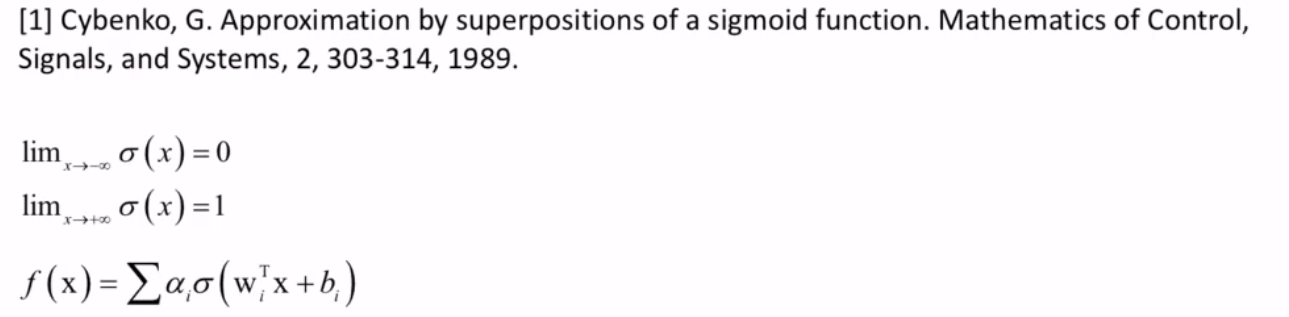
与动物神经系统的区别

人工神经网络实现的细节问题

输入与输出值的设定

许多激活函数（如 Sigmoid、Tanh）在两端梯度趋近于 0（即 “饱和区”）。若输入特征数值过大或过小，会导致激活函数输出进入饱和区，模型丧失学习能力。归一化后，输入被映射到激活函数的 “敏感区”（如 Sigmoid 的中间区域\((-1, 1)\)），保证激活函数能有效传递梯度，让模型保持学习能力。

网络的规模

激活函数的选择

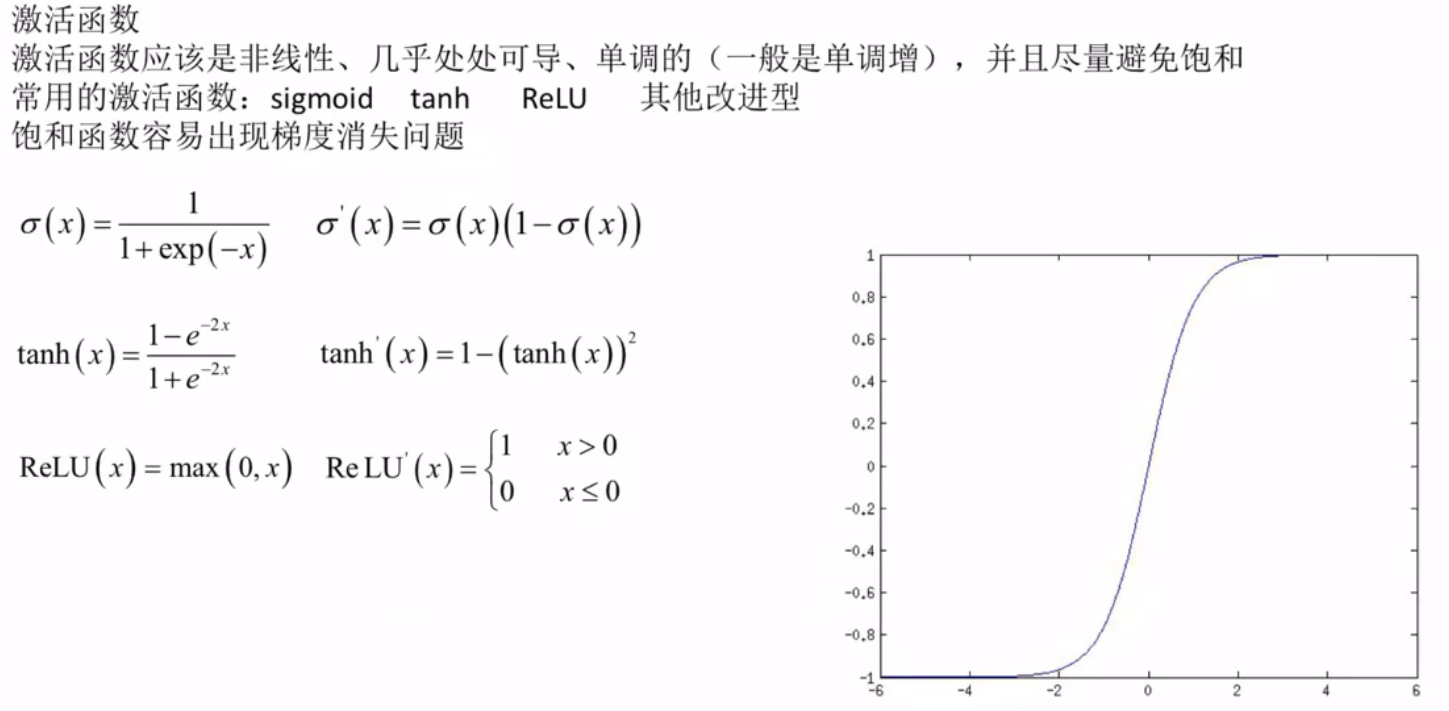
在神经网络中，“激活函数尽量避免饱和” 是指要让激活函数的输出和梯度尽可能处于非饱和区域，避免进入饱和区域。

“激活函数尽量避免饱和” 的本质是保证梯度在反向传播中能有效传递，让深层神经网络的每一层都能更新参数，从而实现高效训练和良好的性能。这也是 ReLU 等非饱和激活函数成为现代神经网络主流选择的核心原因。

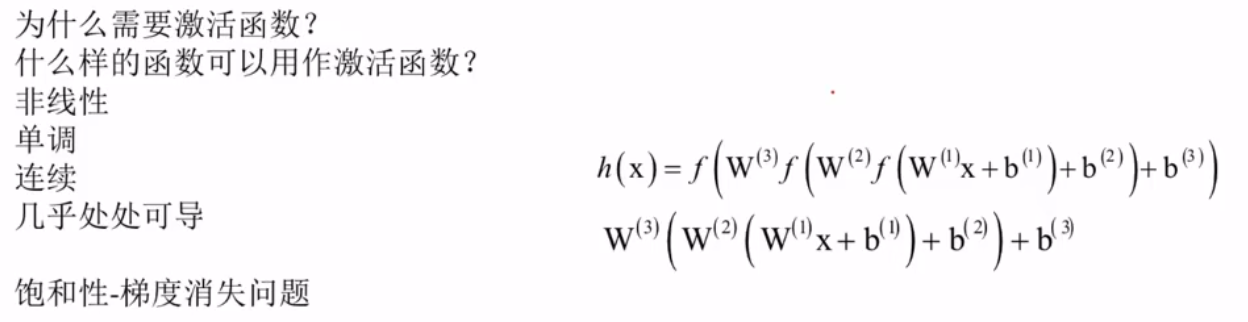
损失函数的选择

分类问题采用交叉熵：

从计算过程能看出，欧氏距离衡量的是 “向量各维度数值偏差的综合大小”，但完全没考虑 “概率分布的合理性”—— 比如[0.9, 0.1]是更接近真实标签[1,0]的概率分布（分类更准确），而[0.6, 0.4]的分类可信度低，但欧氏距离仅用 “数值差的平方和” 来量化差异，无法突出 “分类正确性” 的核心需求，这也是它不适合分类任务的原因之一。

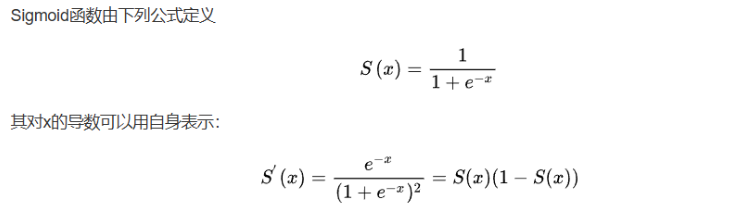Sigmoid函数在第二章

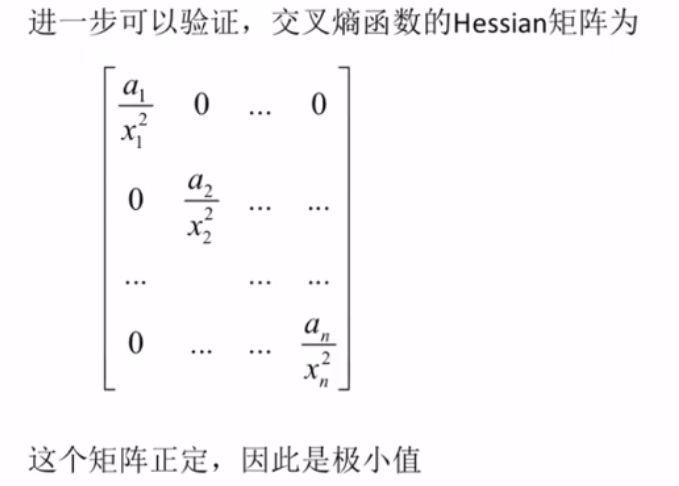
交叉熵函数深入理解

权重的初始化

正则化（防止过拟合）

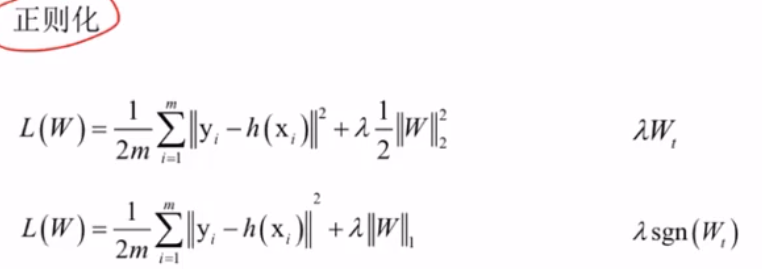
正则化的本质是在损失函数中引入 “复杂度约束”，通过 L2 的 “权重衰减” 或 L1 的 “稀疏化 / 特征选择”，限制模型过度学习训练数据的细节，从而让模型在未知数据上表现更好（泛化能力更强）。这是机器学习从 “训练集拟合” 到 “真实场景应用” 的关键保障，也是解决过拟合问题的核心手段之一。

学习率的设定

人工神经网络面临的问题

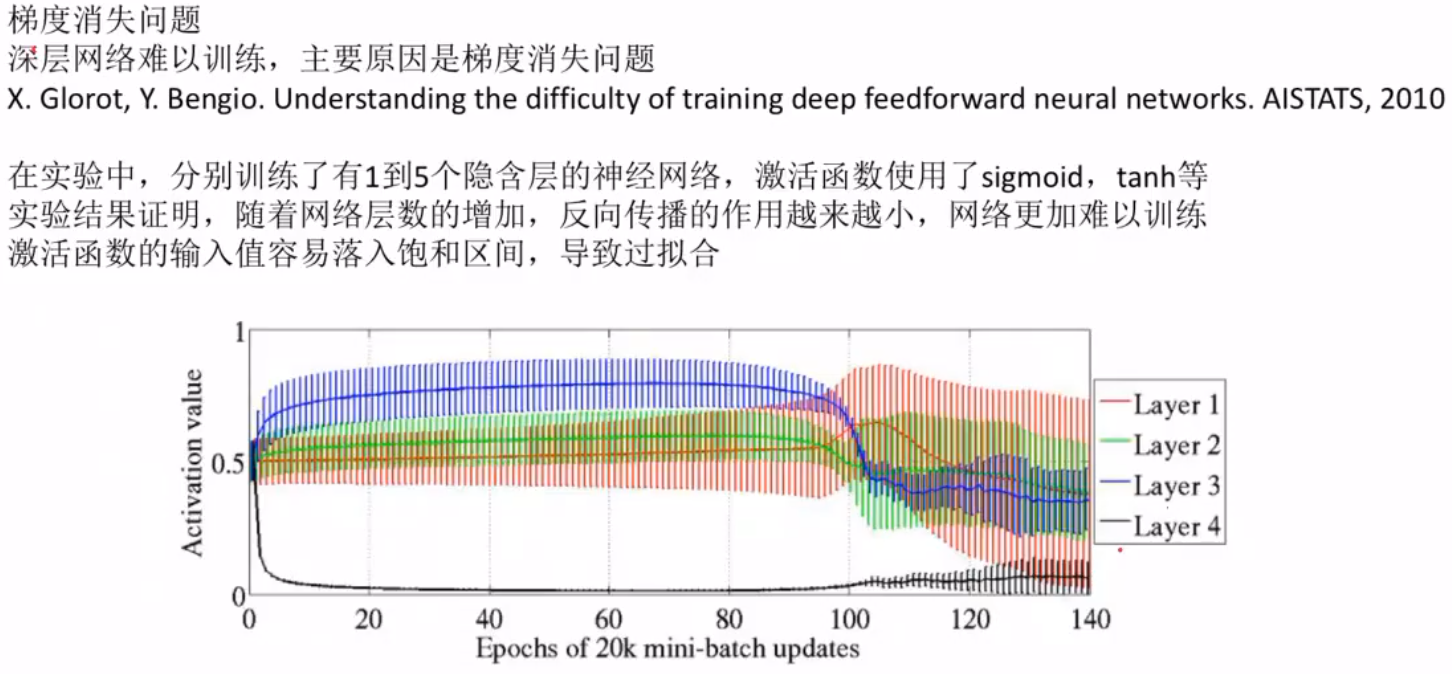
1梯度消失问题

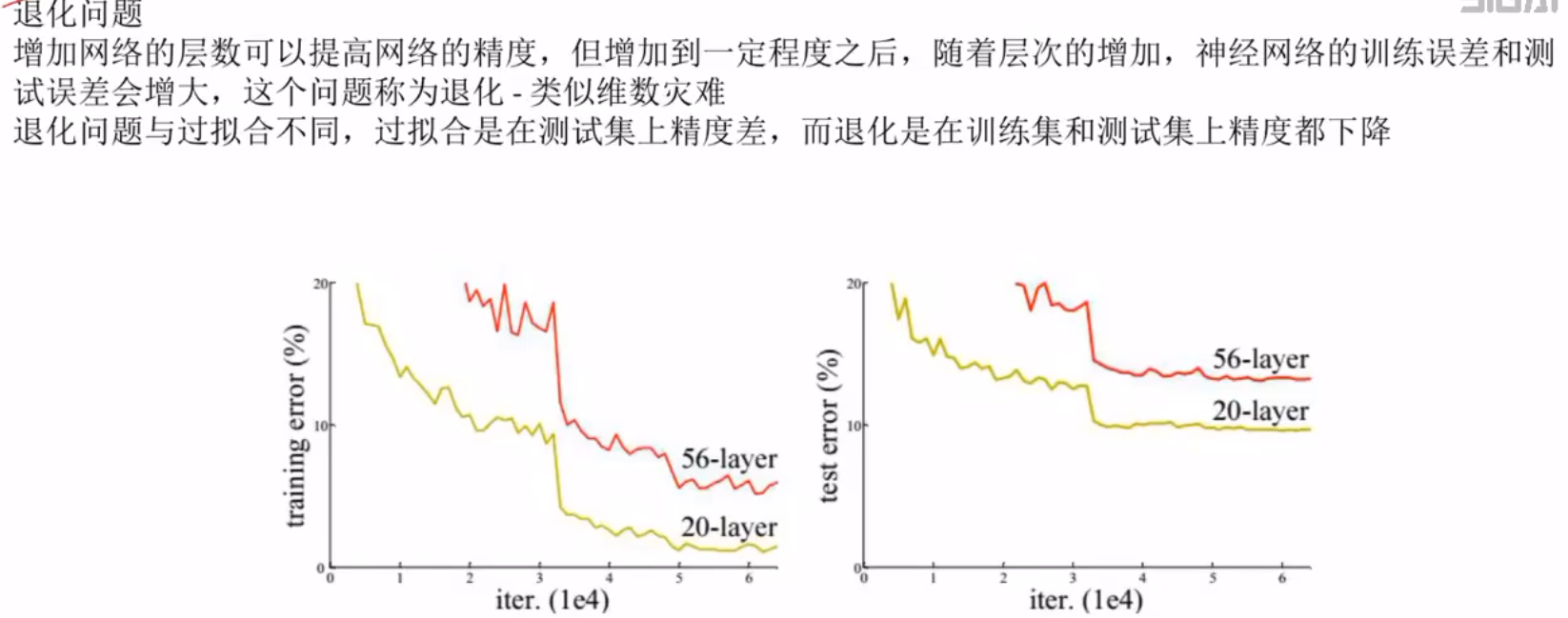
2退化

3局部极小值

4鞍点问题

梯度消失问题

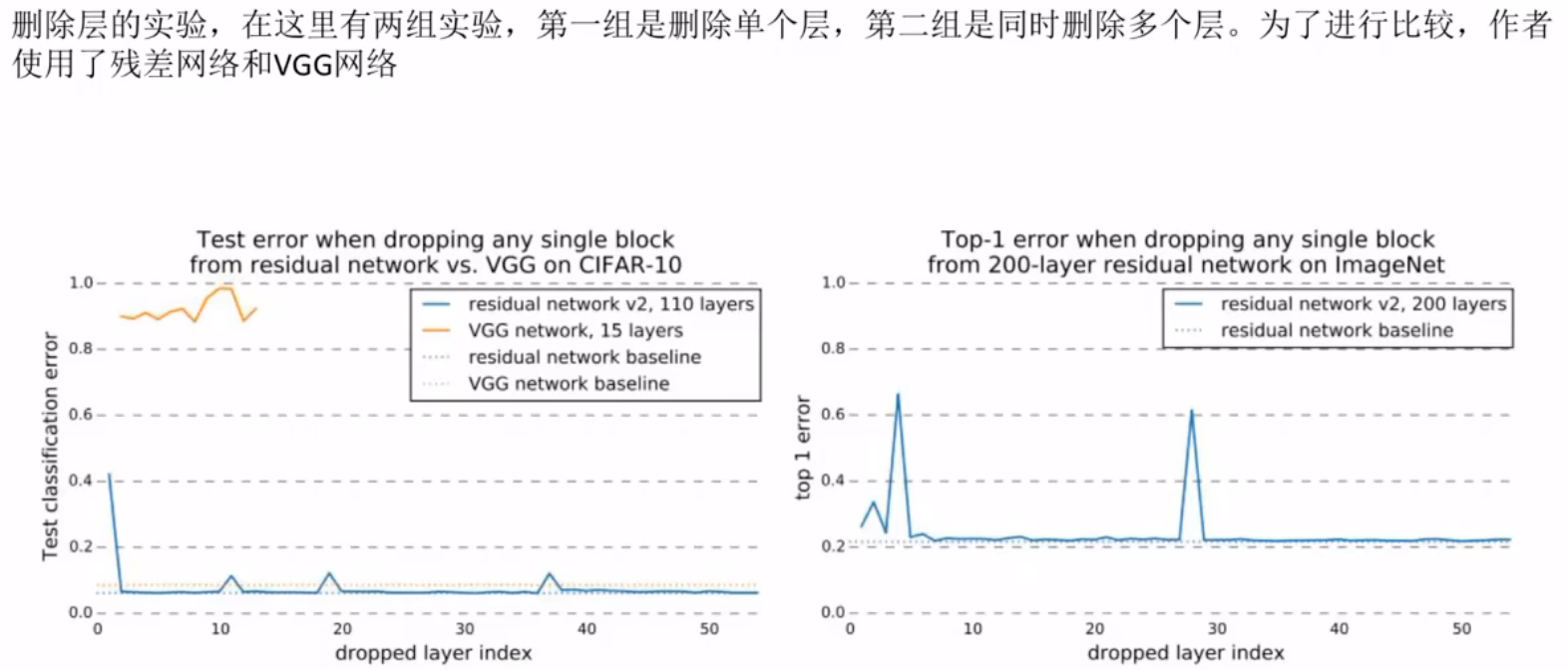
退化问题（在训练集和测试集上表现都很差）

残差网络和高速公路网络是对应的解决问题

局部极值问题

鞍点问题

典型应用

自己动手尝试做个实验。

四.深度学习简介

机器学习面临的挑战

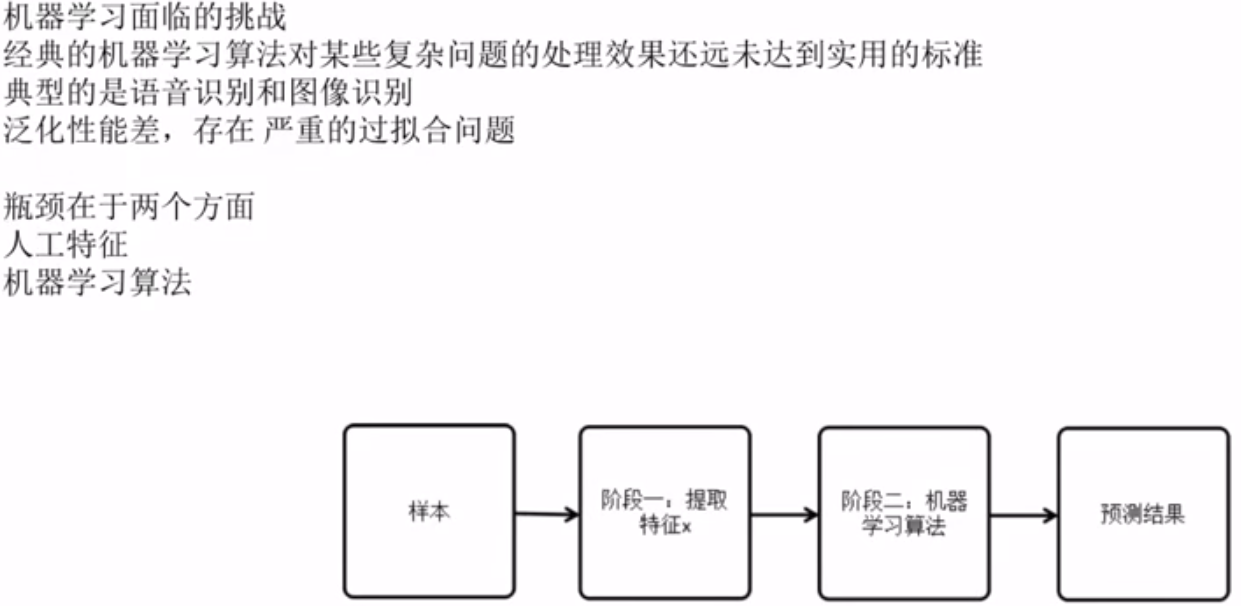
人工特征的局限性

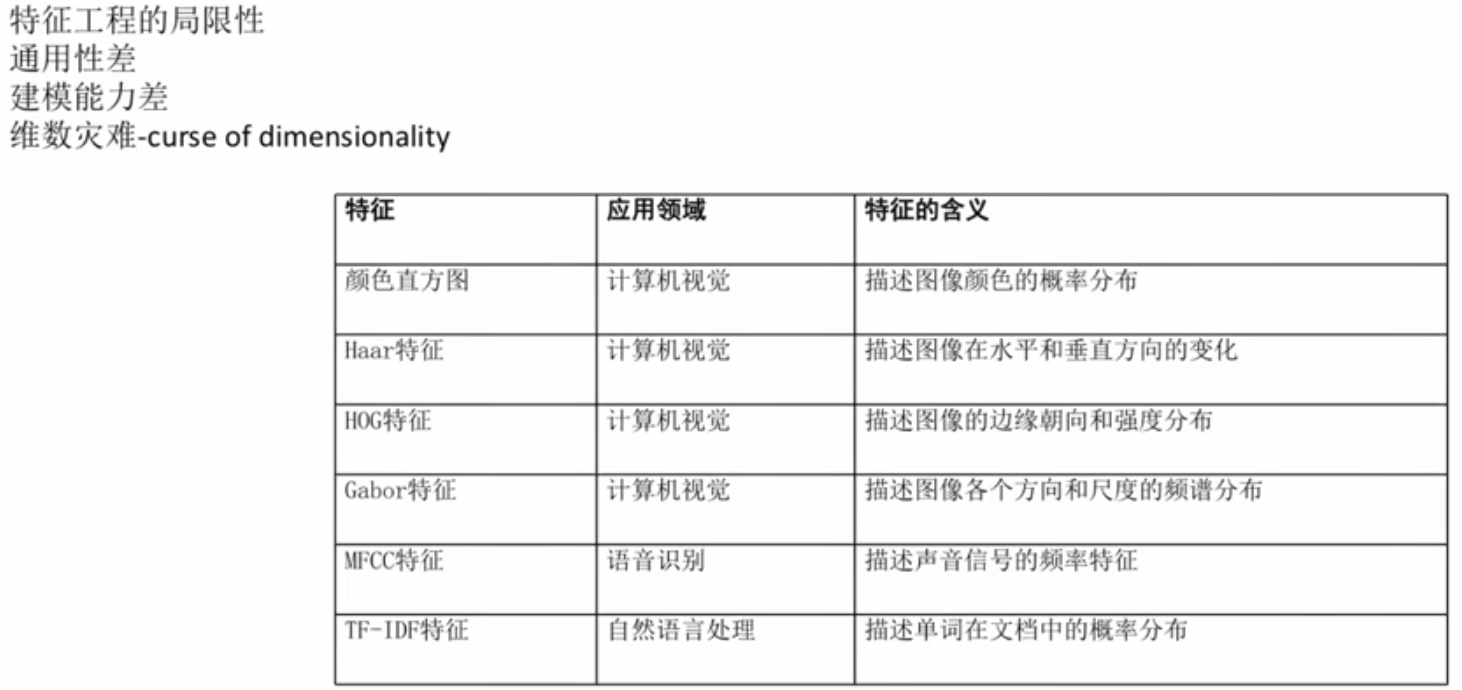
机器学习算法的瓶颈

为什么选择了神经网络

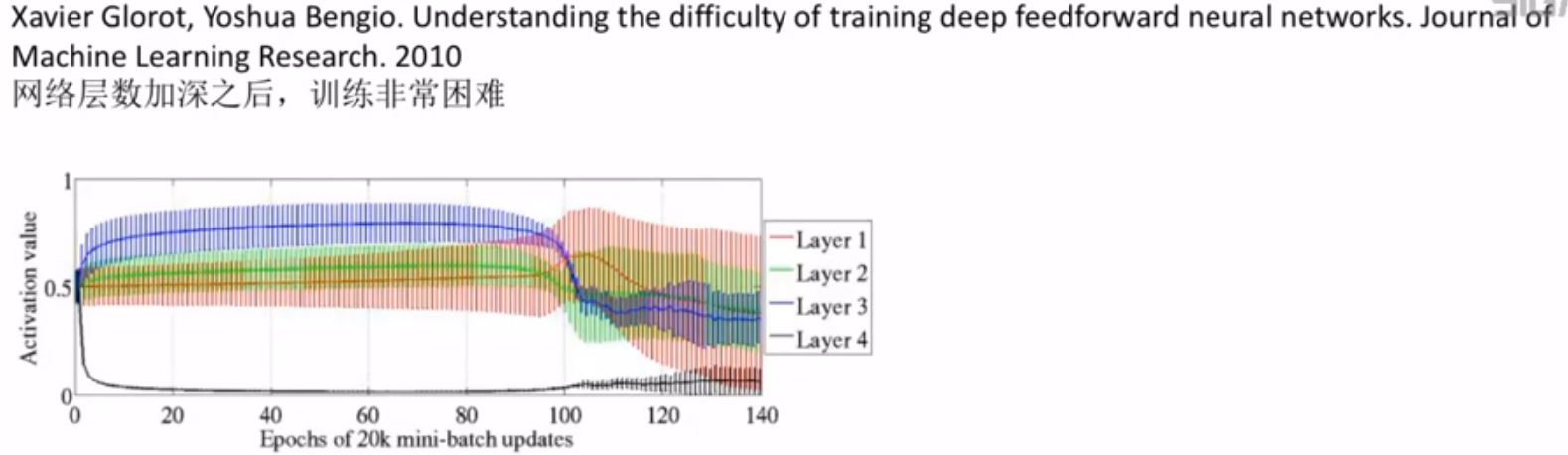
深度学习的困难

诞生阶段

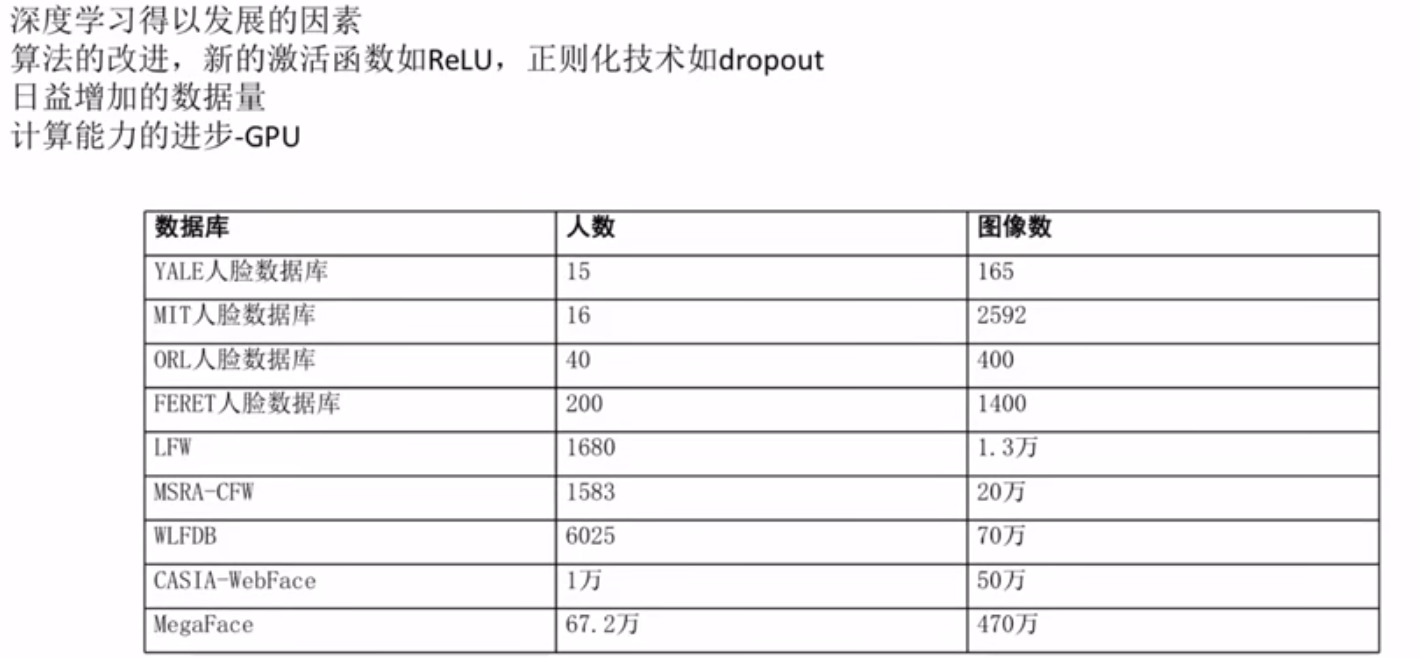
深度学习发展的因素

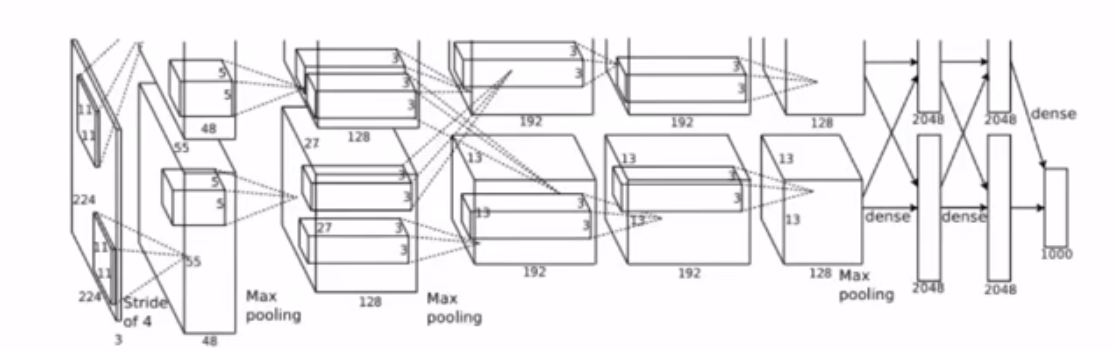
典型的网络结构

发展现状

在机器视觉中的应用

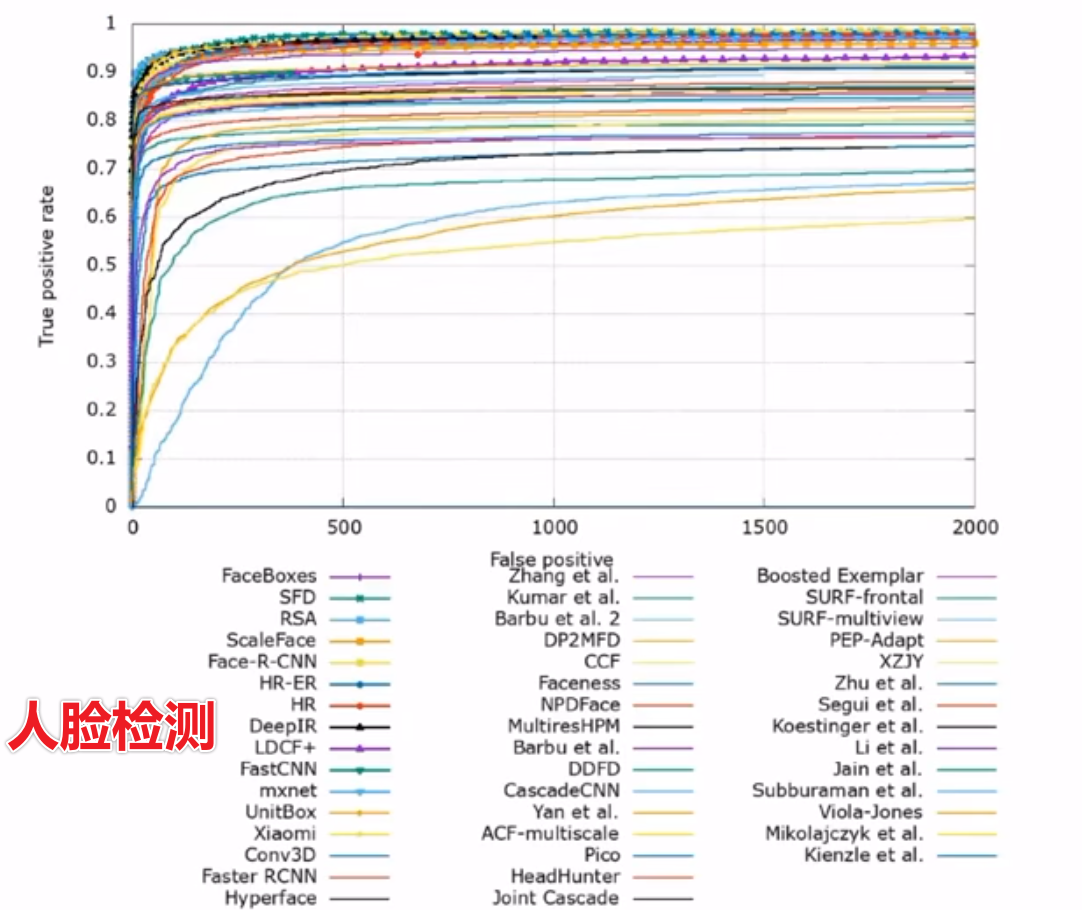
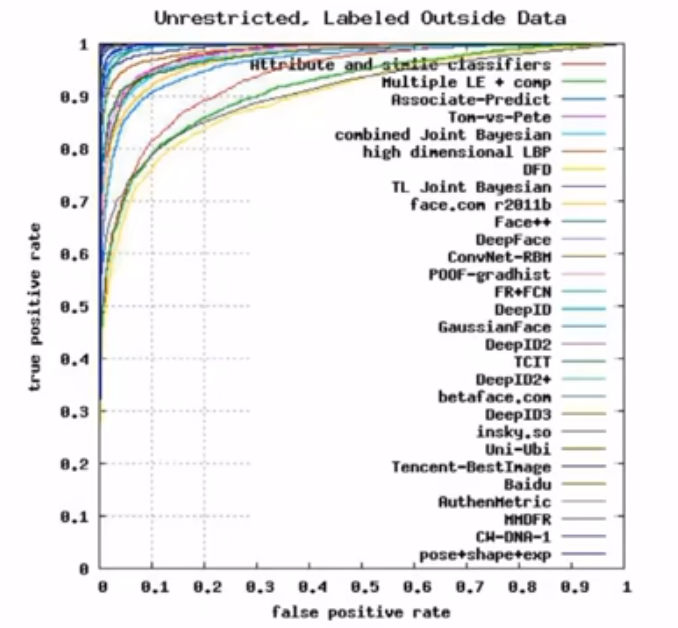
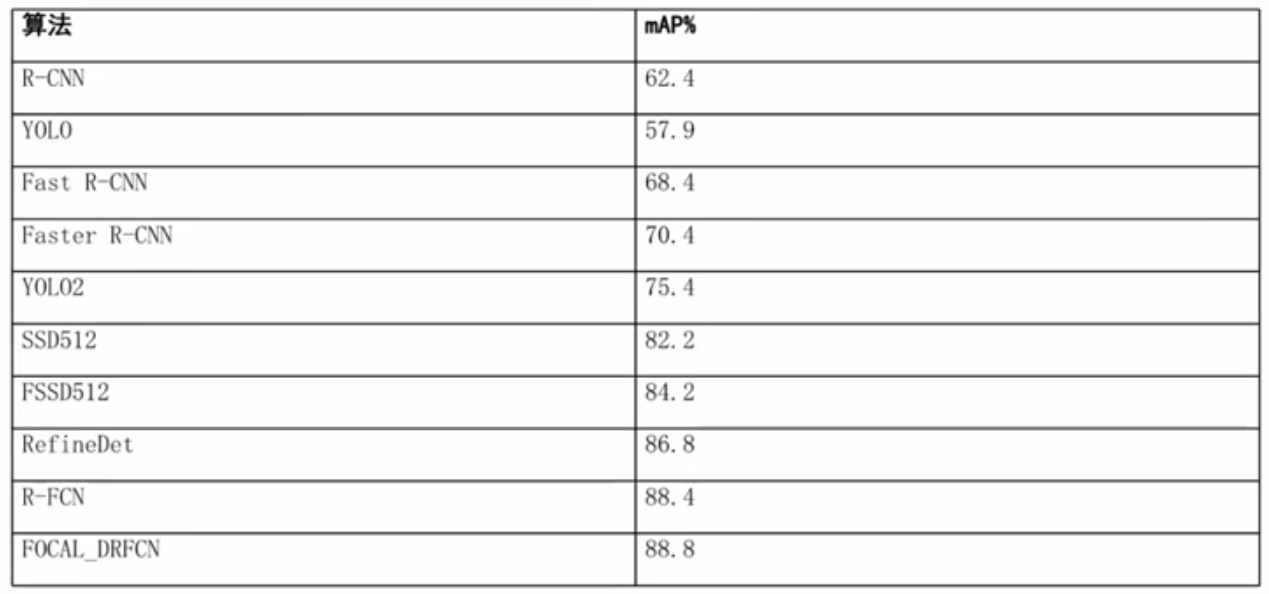
在语音识别中的应用

在自然语言处理中的应用

在推荐系统中的应用

深度强化学习简介

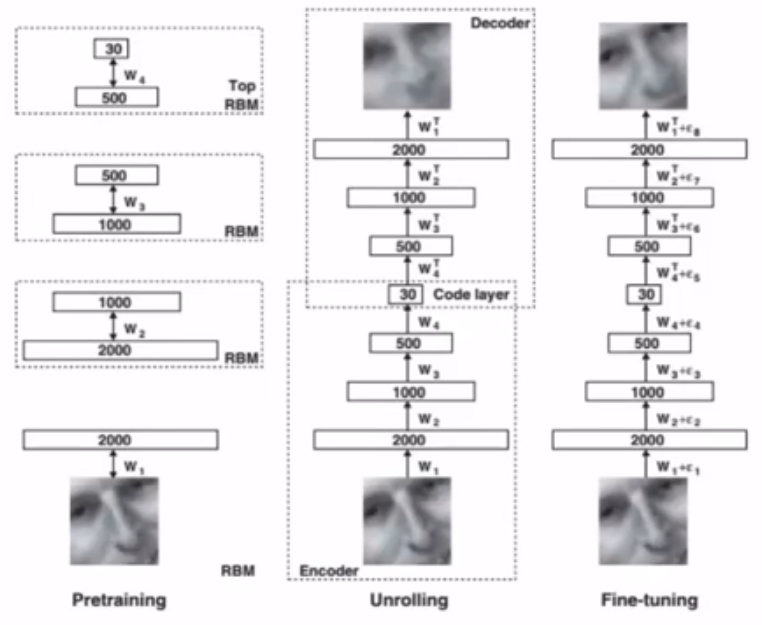
五.自动编码器AE

自动编码器的基本思想

网络结构

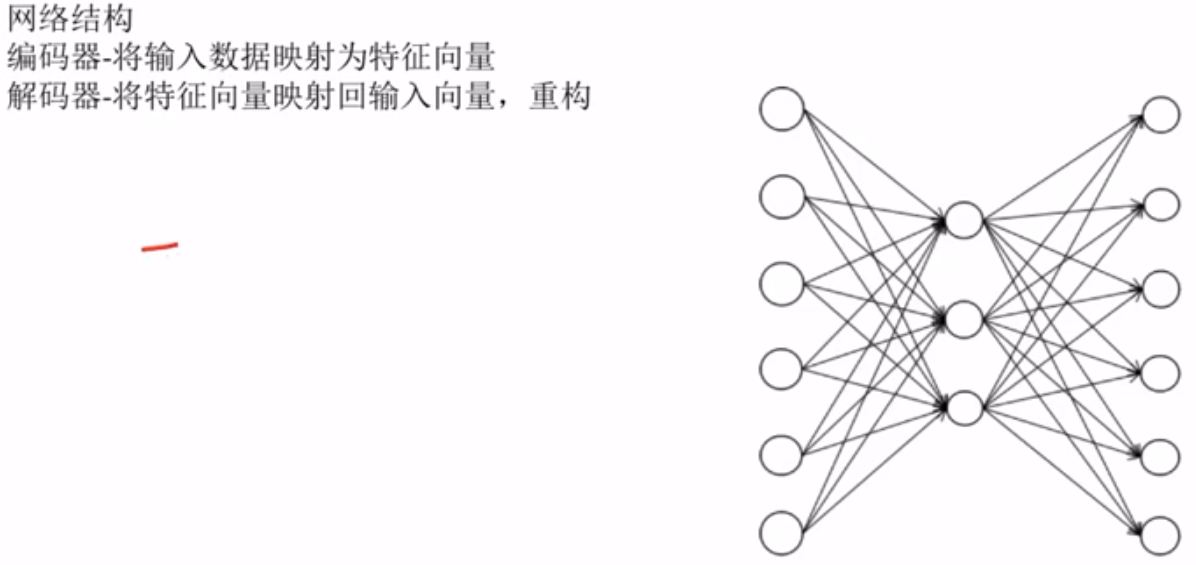
损失函数

实际应用——特征提取

去噪自动编码器

稀疏自动编码器

收缩自动编码器

多层编码器

六.受限玻尔兹曼机

玻尔兹曼分布

网络结构

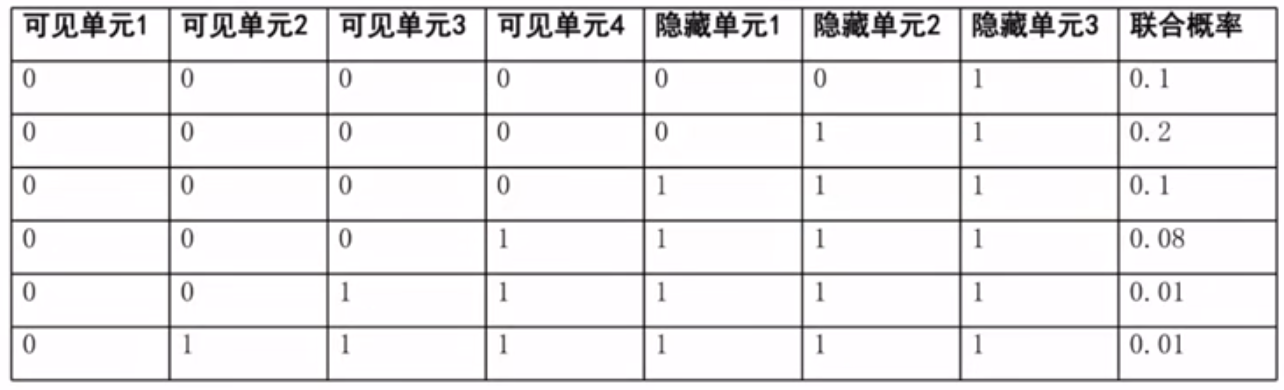
计算隐藏单元的条件概率

计算单个隐藏单元的值

用于特征提取

训练算法

深度玻尔兹曼机

七.卷积神经网络

卷积神经网络简介

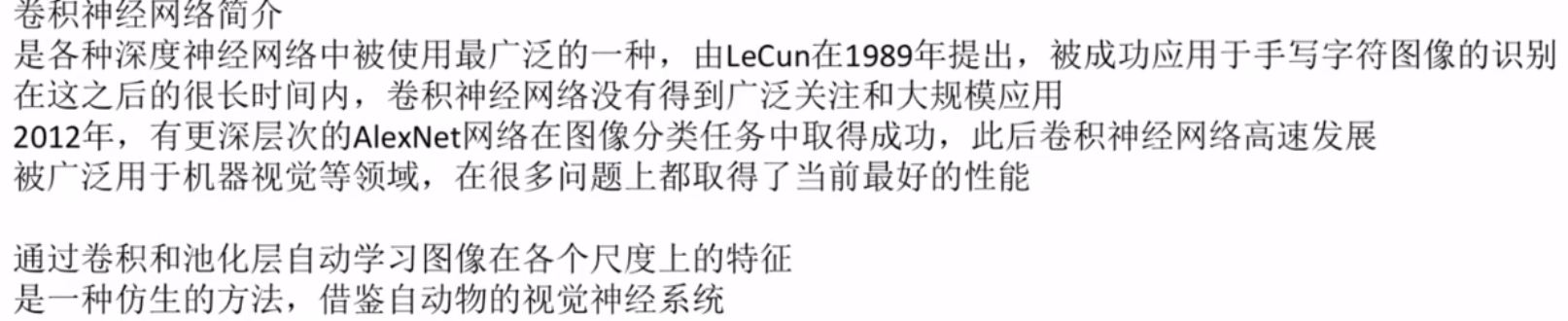
视觉神经系统的原理

卷积神经网络的核心思想

卷积运算

水平边缘检测

卷积层的原理

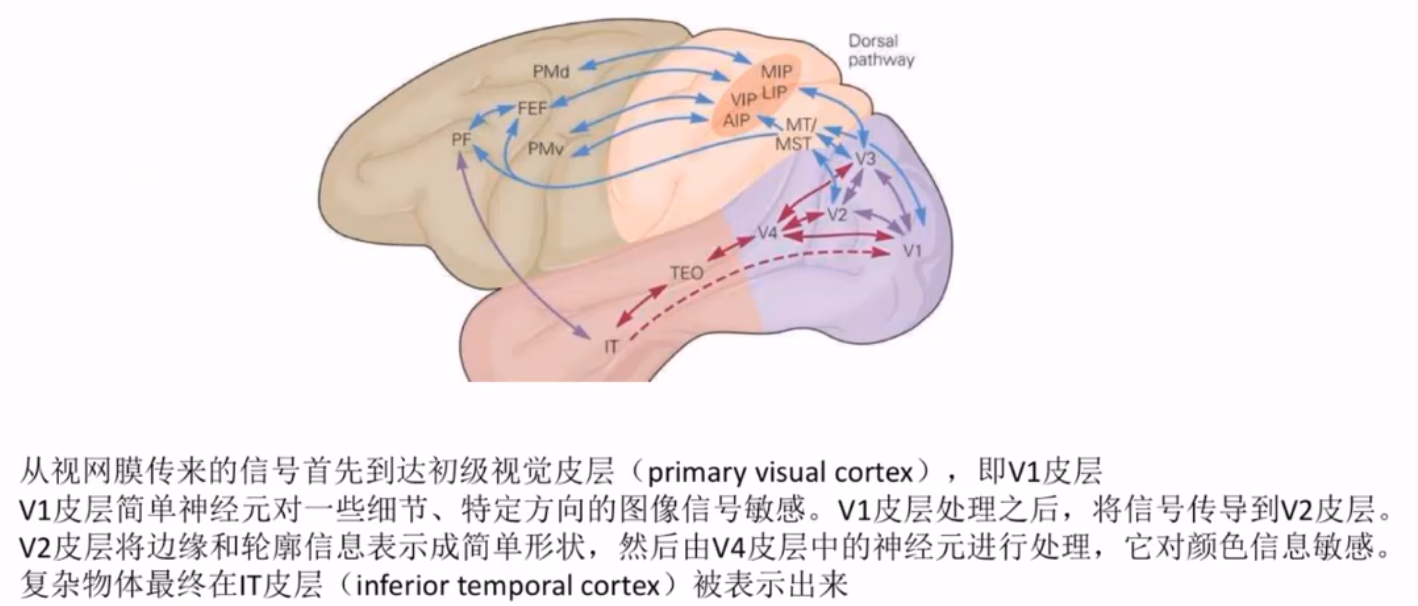
多通道卷积

池化层的原理

全连接层

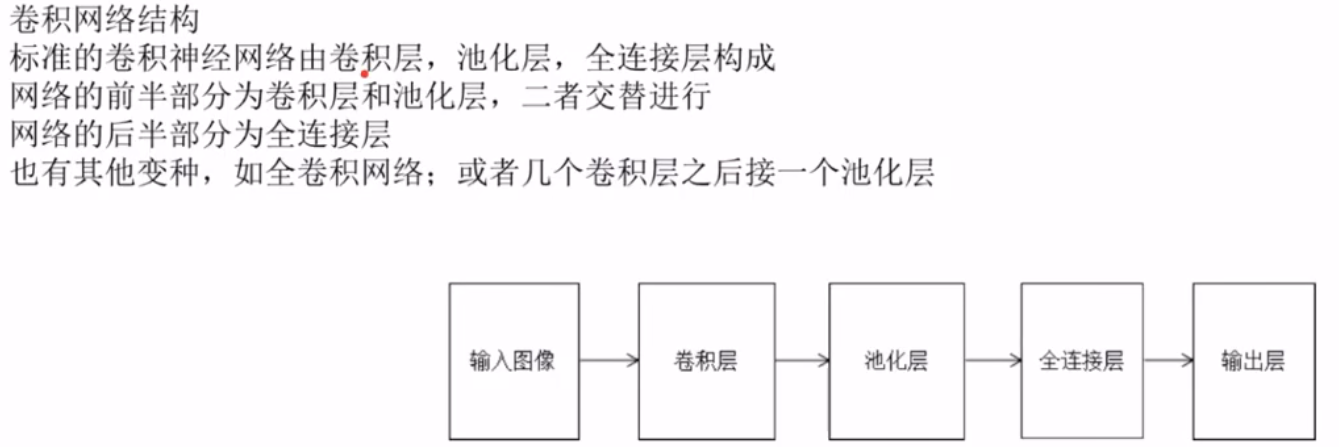
卷积神经网络的整体结构

训练算法简介

卷积层的反向传播

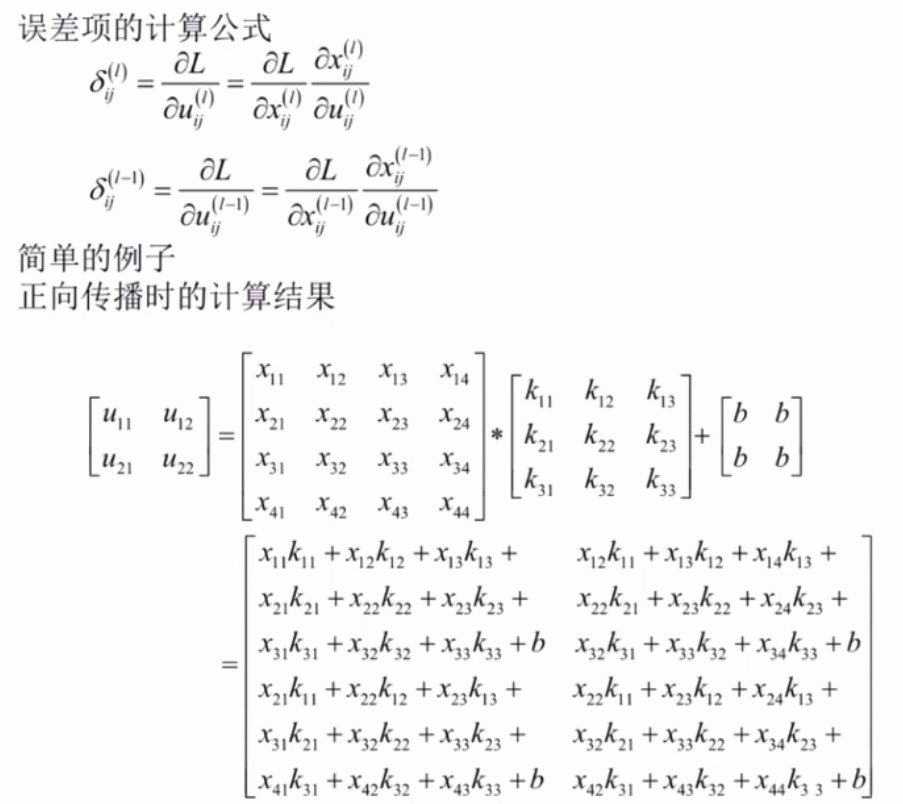
池化层的反向传播

全连接层的反向传播

完整的反向传播算法

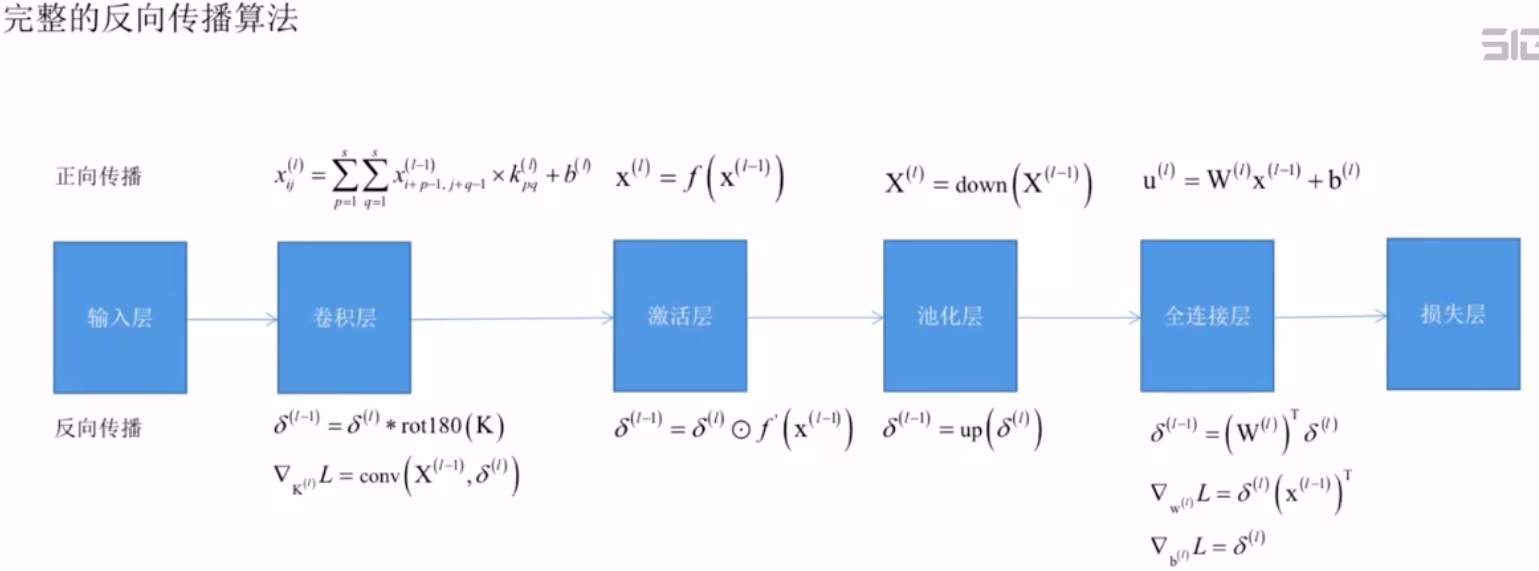
随机梯度下降法

参数的初始化

学习率

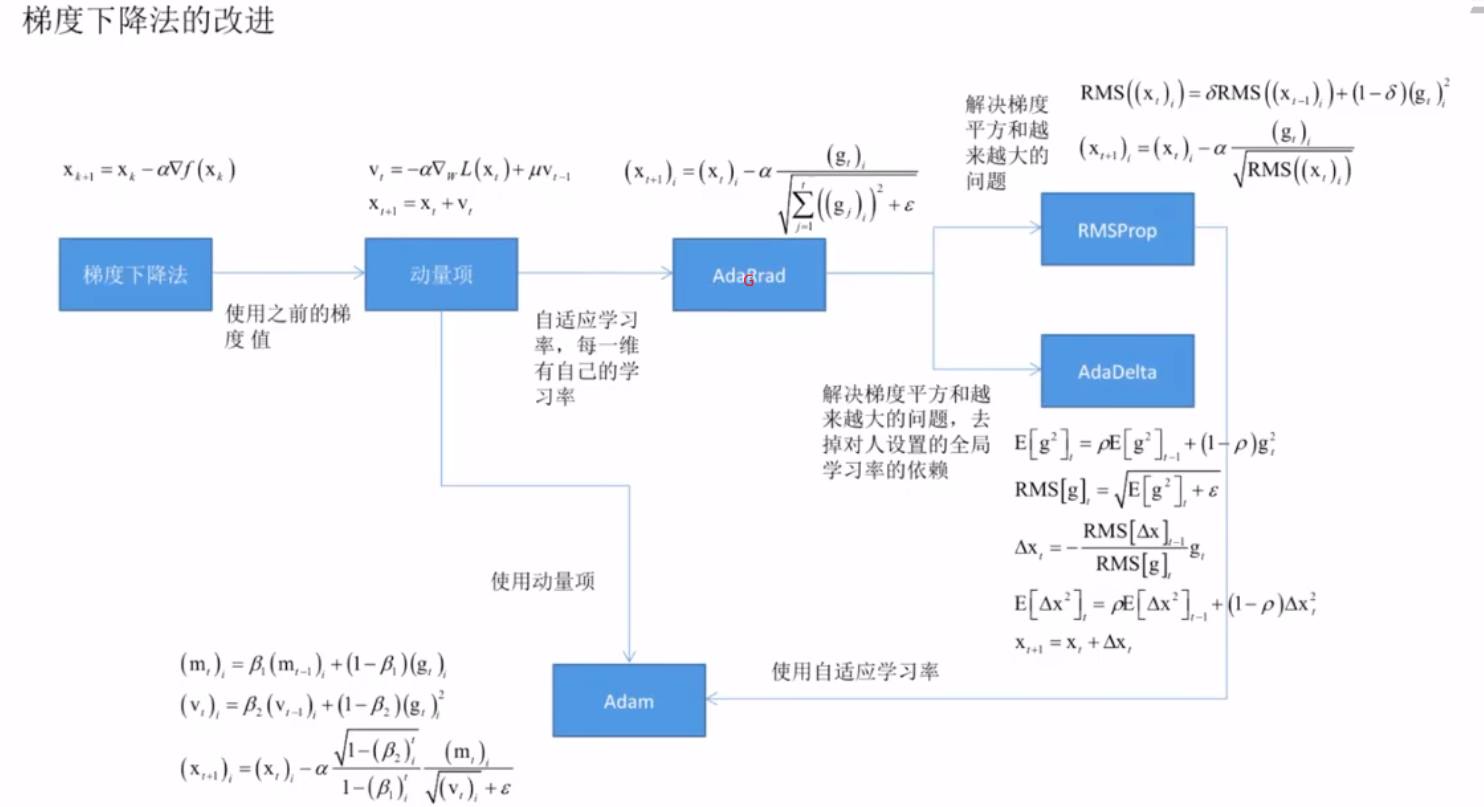
动量项梯度下降法

AdaGrad算法

RMSProp算法

AdaDelta算法

Adam算法

梯度下降法的改进

迁移学习与finr tune

八.经典的神经网络

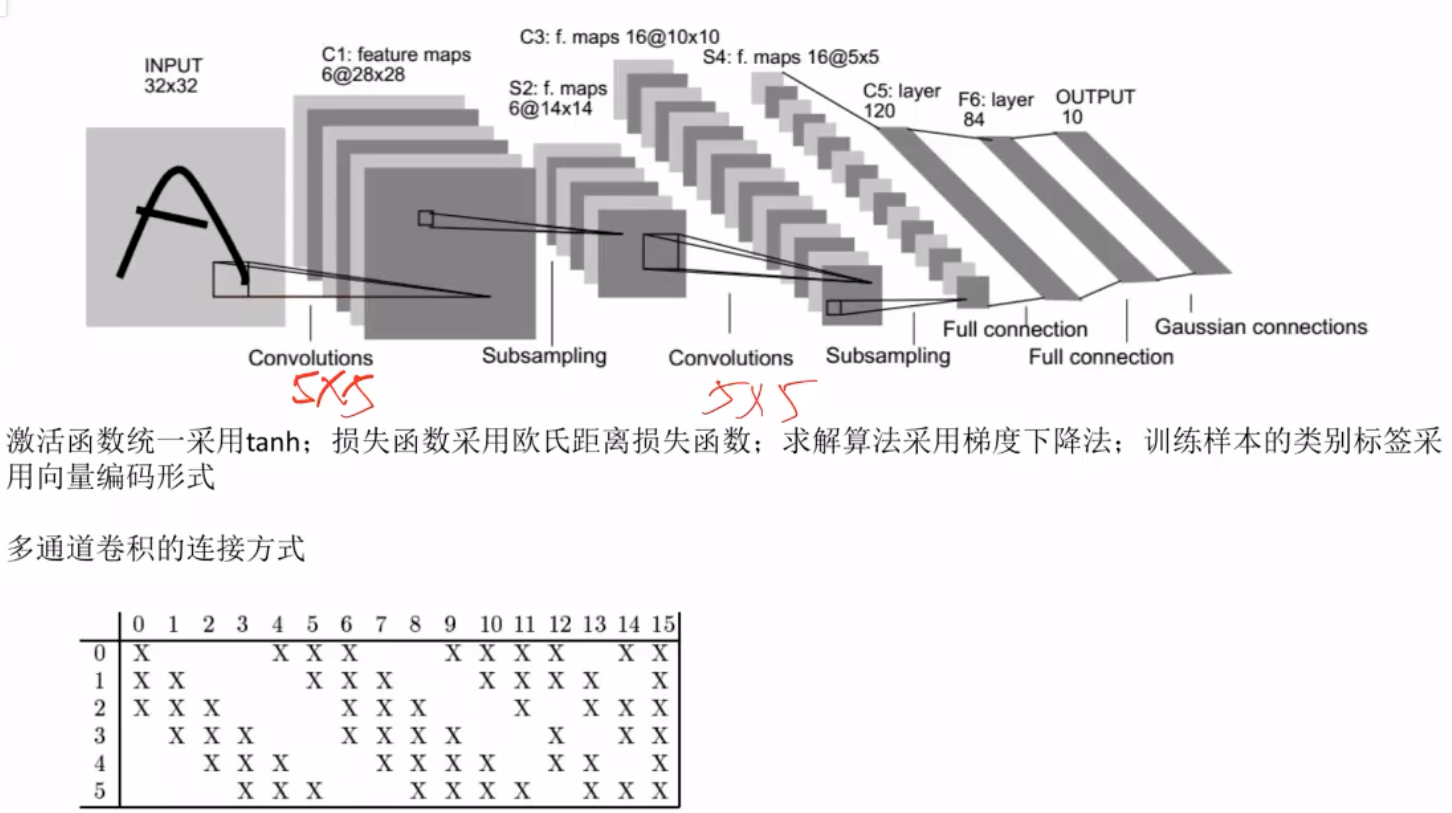
LeNet网络

LeNet网络的结构

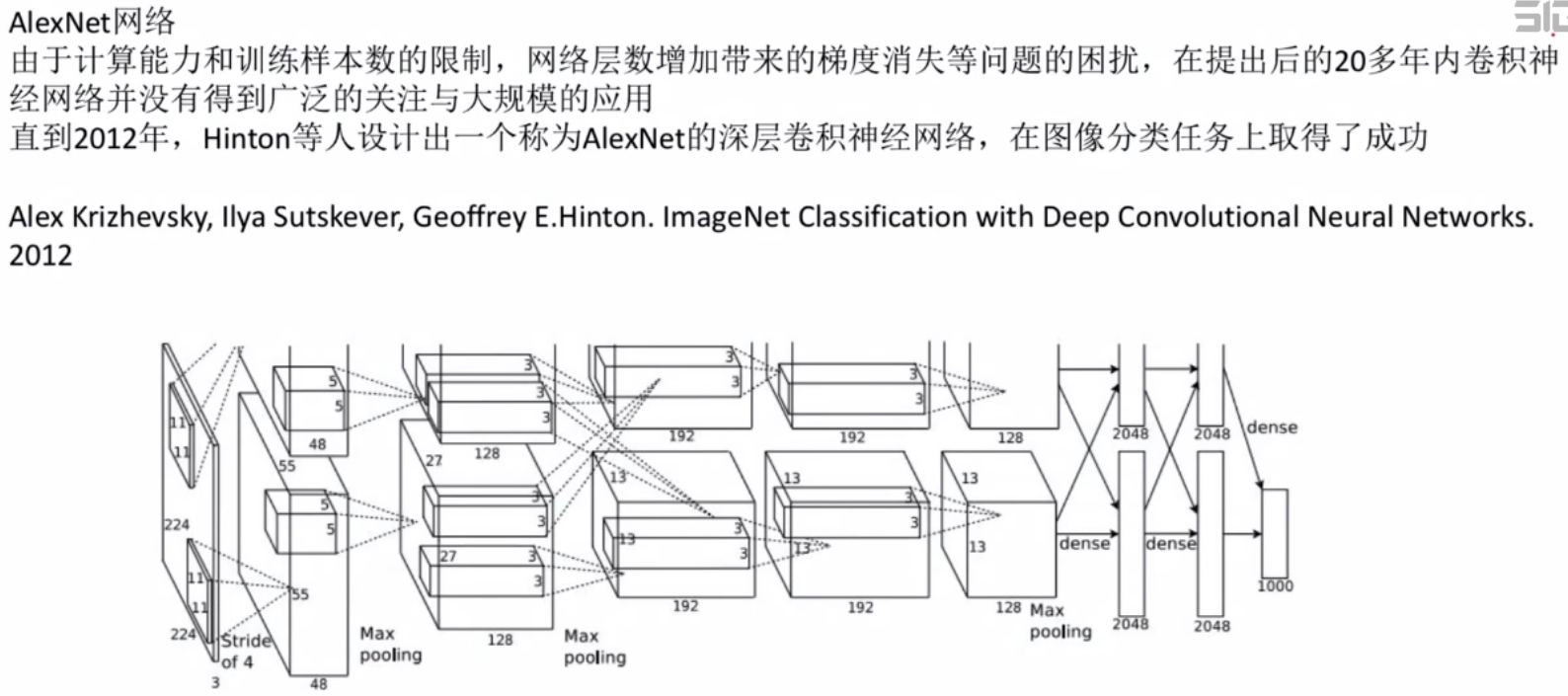
AlexNet网络

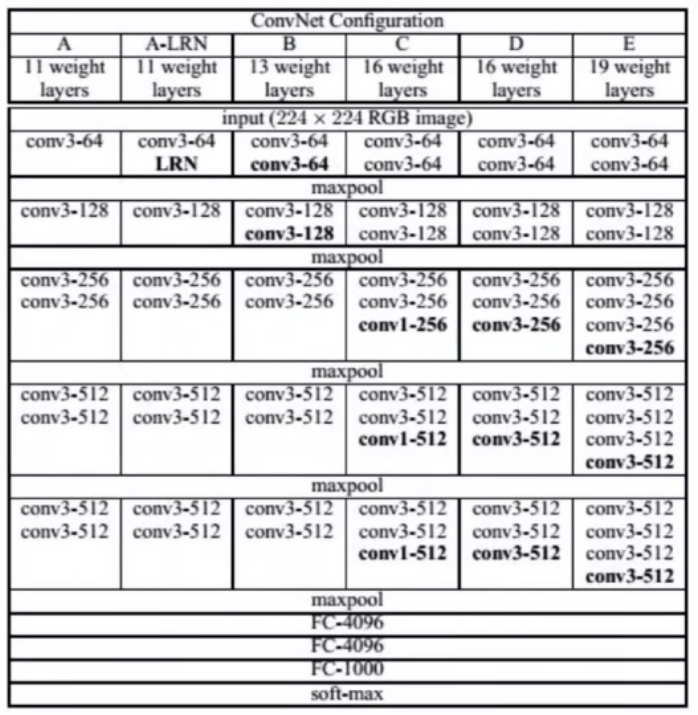
VGG网络

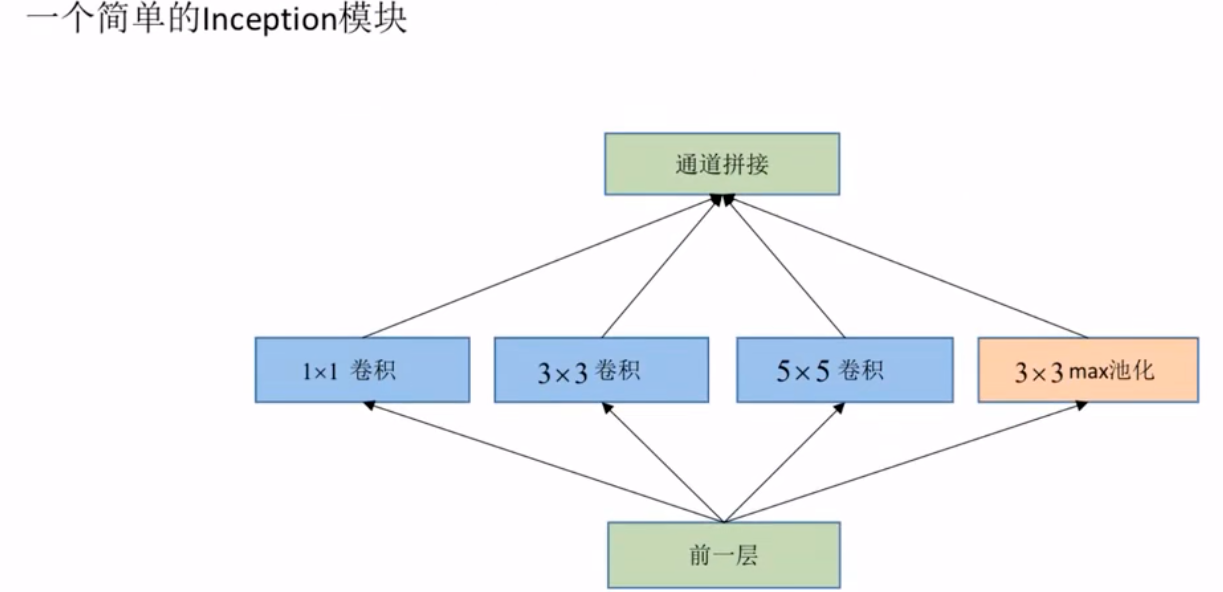
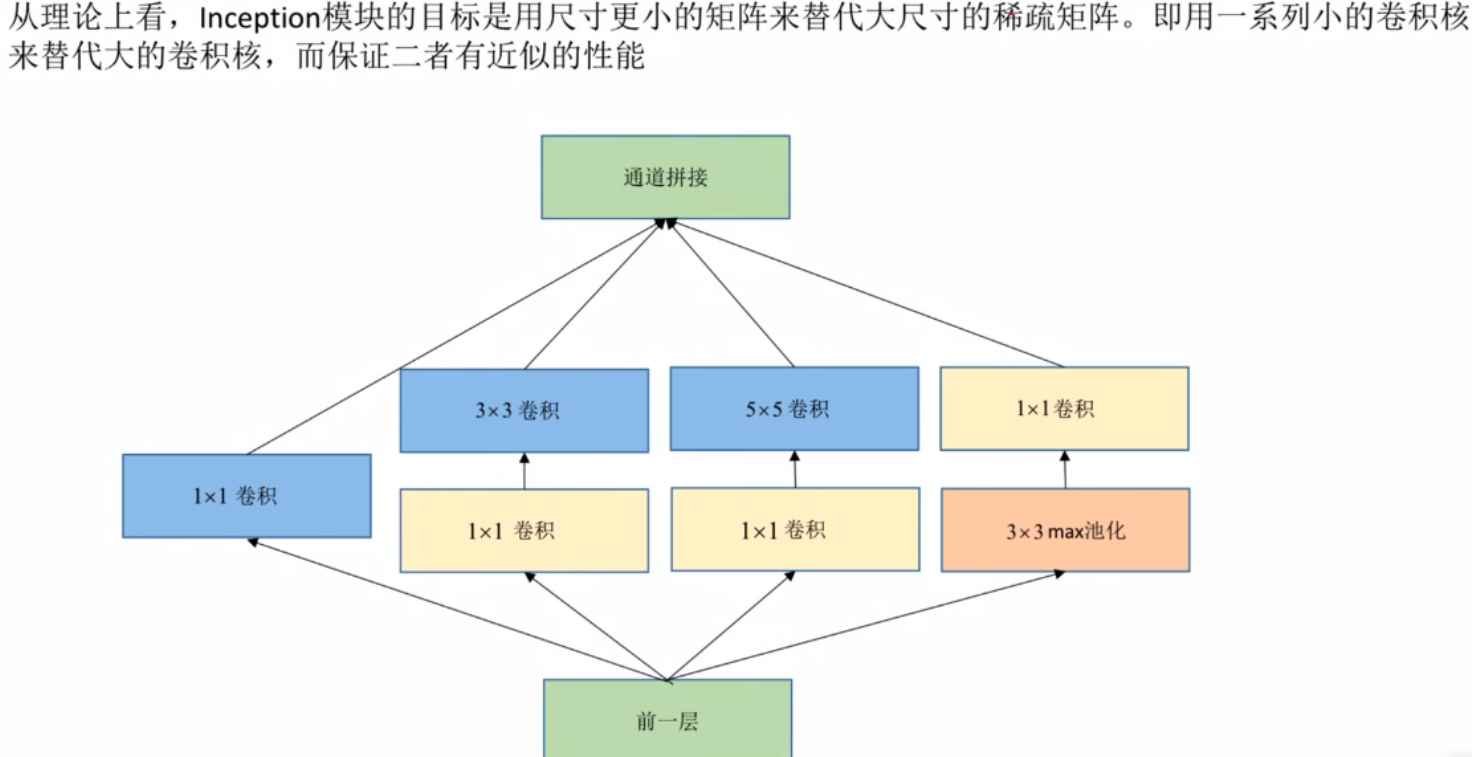
GoogLeNet网络

反卷积运算

卷积的可视化

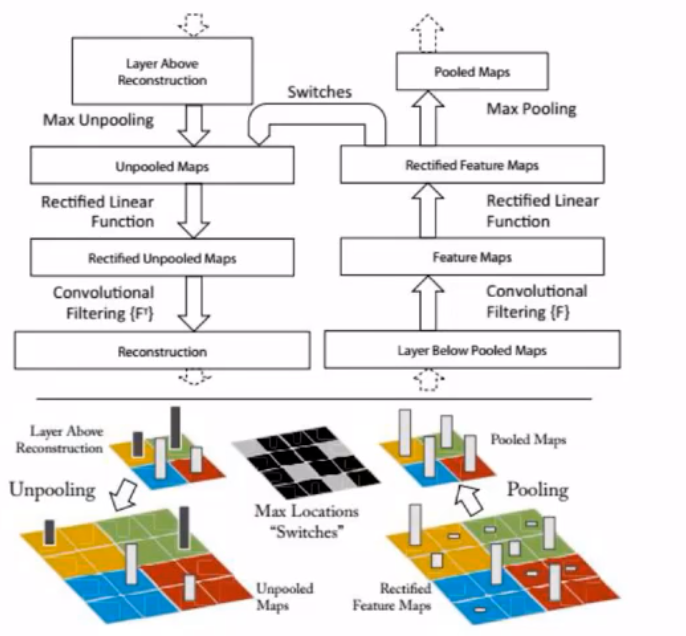
卷积神经网络的数学特性

根据卷积重构图像

九.卷积神经网络面临的挑战

深度消失问题

退化问题

总体改进措施

卷积层改进

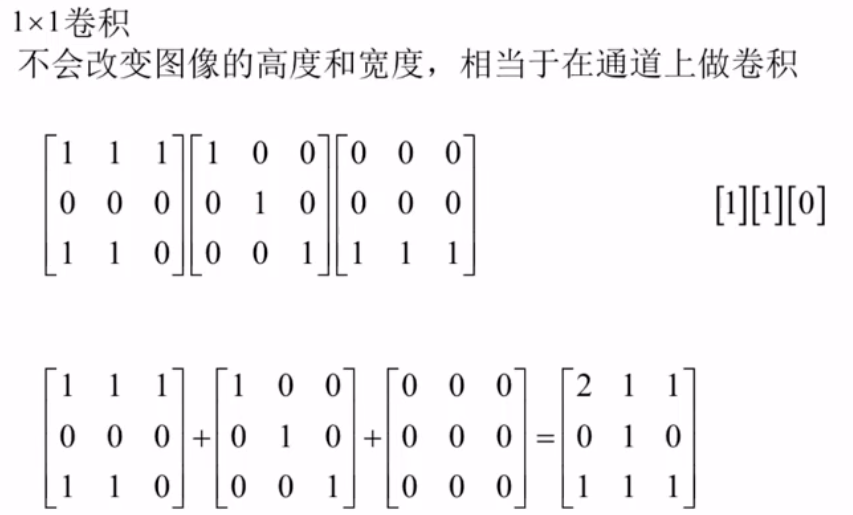
3个通道变成1个通道了。

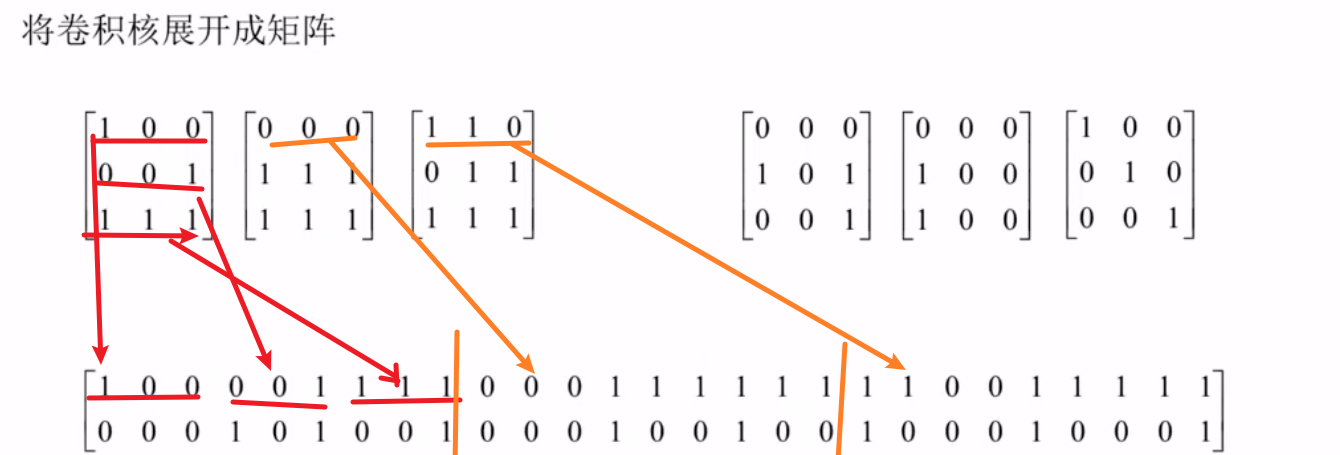
用矩阵乘法实现卷积运算

举个例子

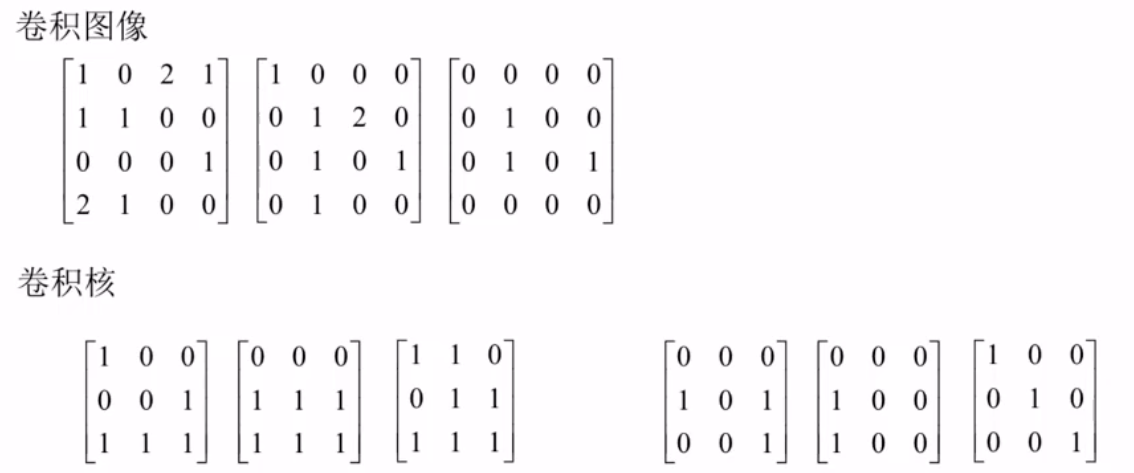
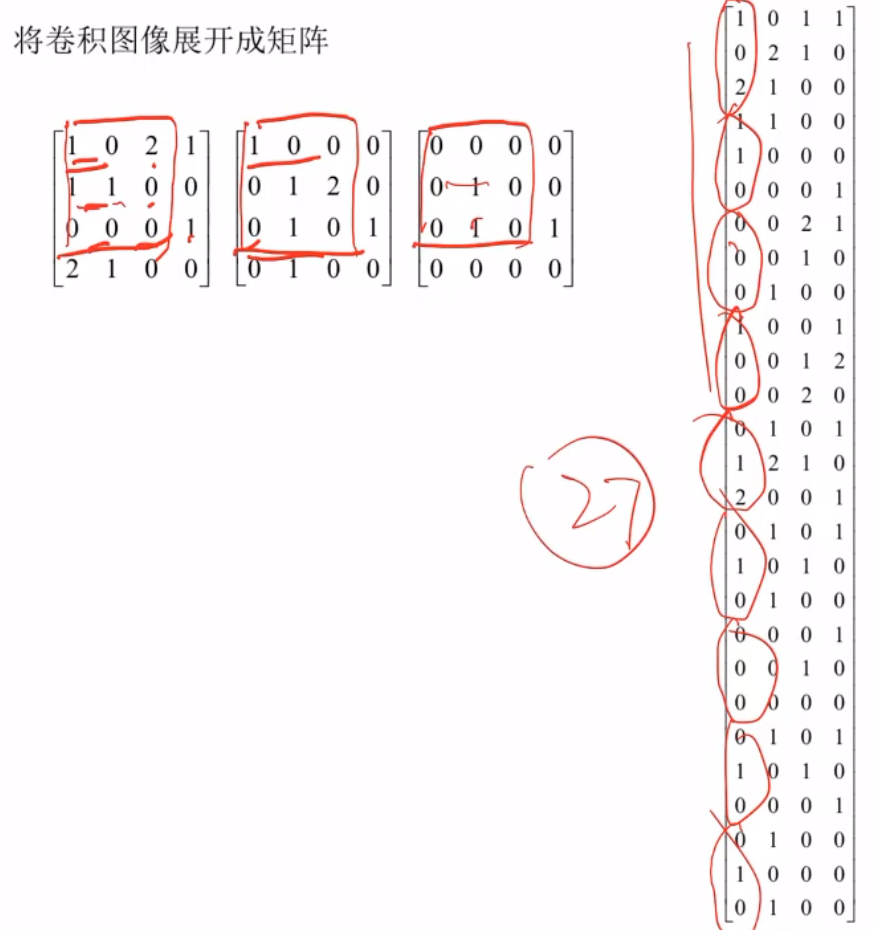
图像是四行四列，卷积核的大小是三行三列，做卷积运算的话，只能做四次，卷积核与图像的前三行能做两下（一下是图像左上角3×3的矩阵，一下是右移一位的3×3的矩阵），剩下两下就是图像下移一行的两个（一个是最左边的3×3矩阵，另一个是右移一位的3×3的矩阵）。

池化层的改进

损失函数的改进

十.网络结构的改进

高速公路网络

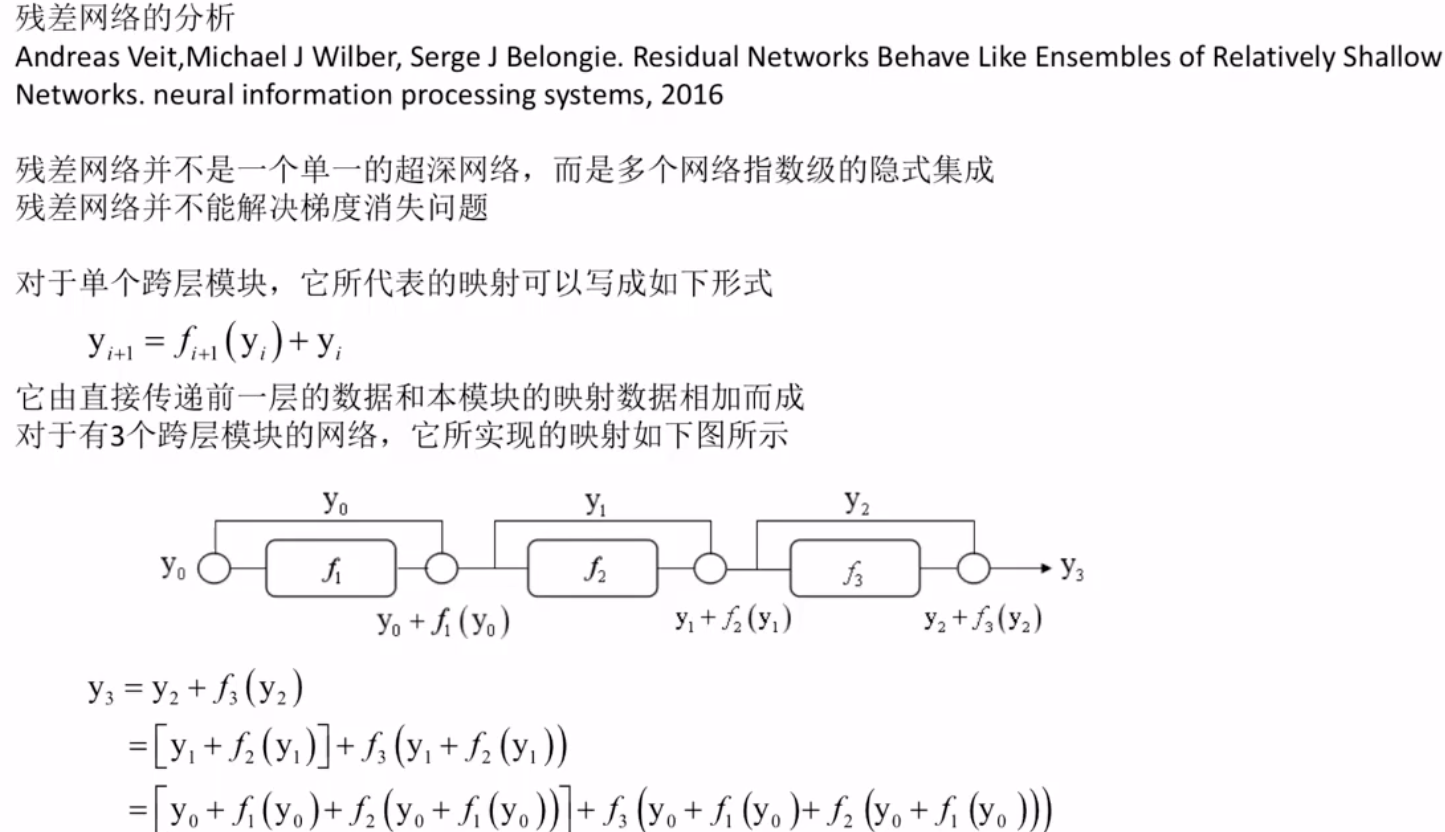
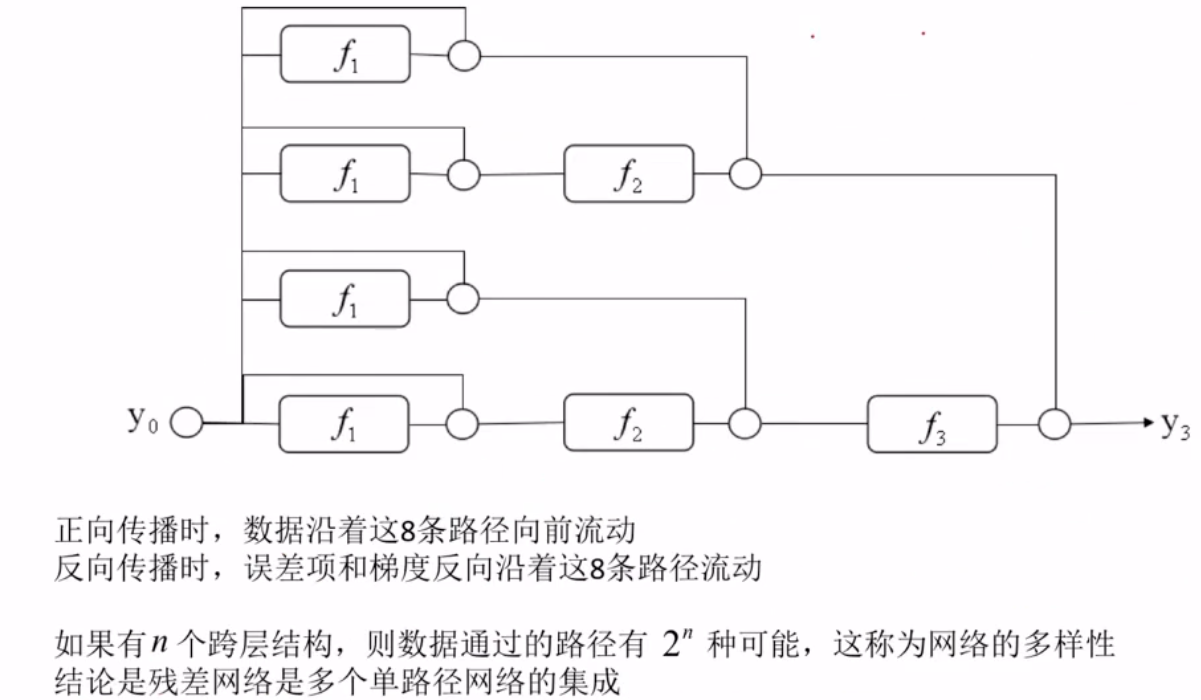
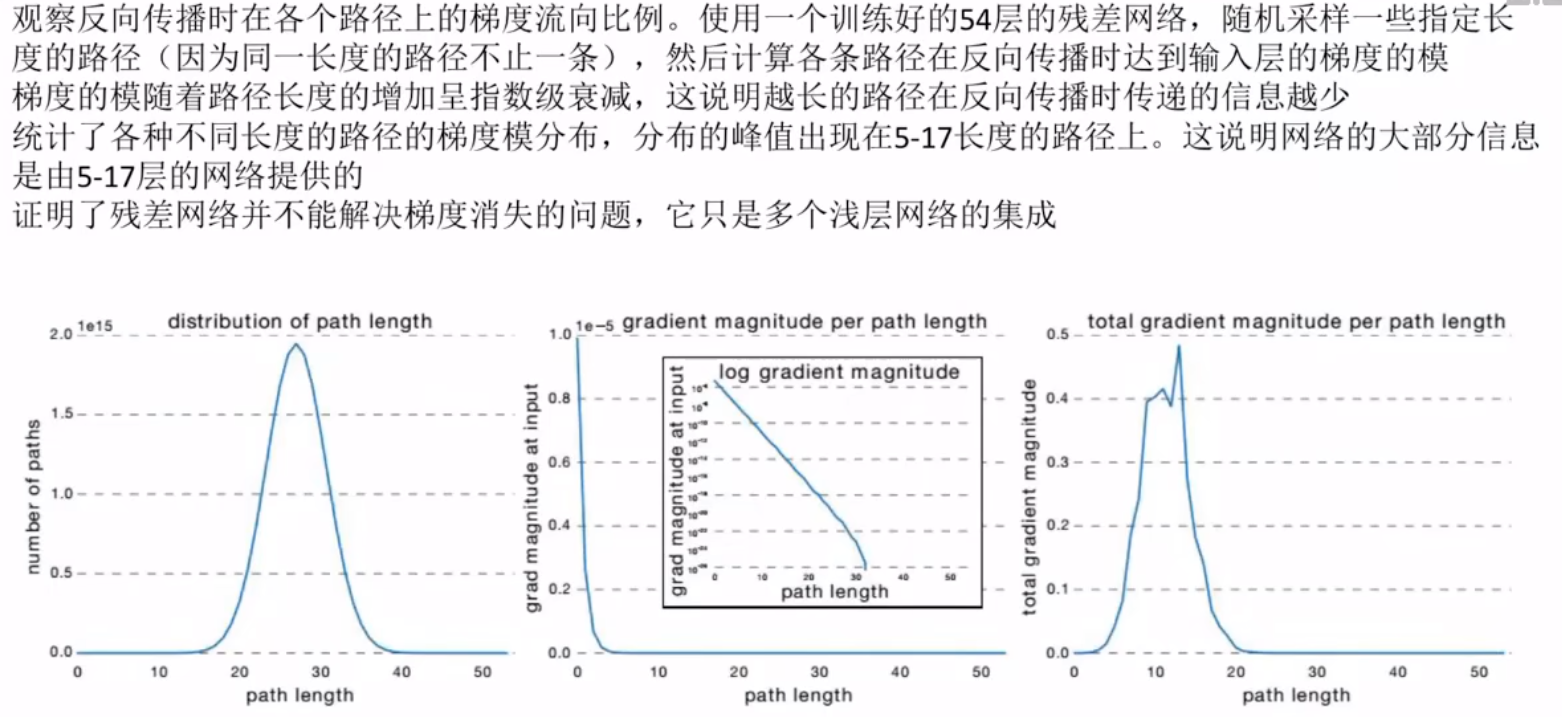
残差网络

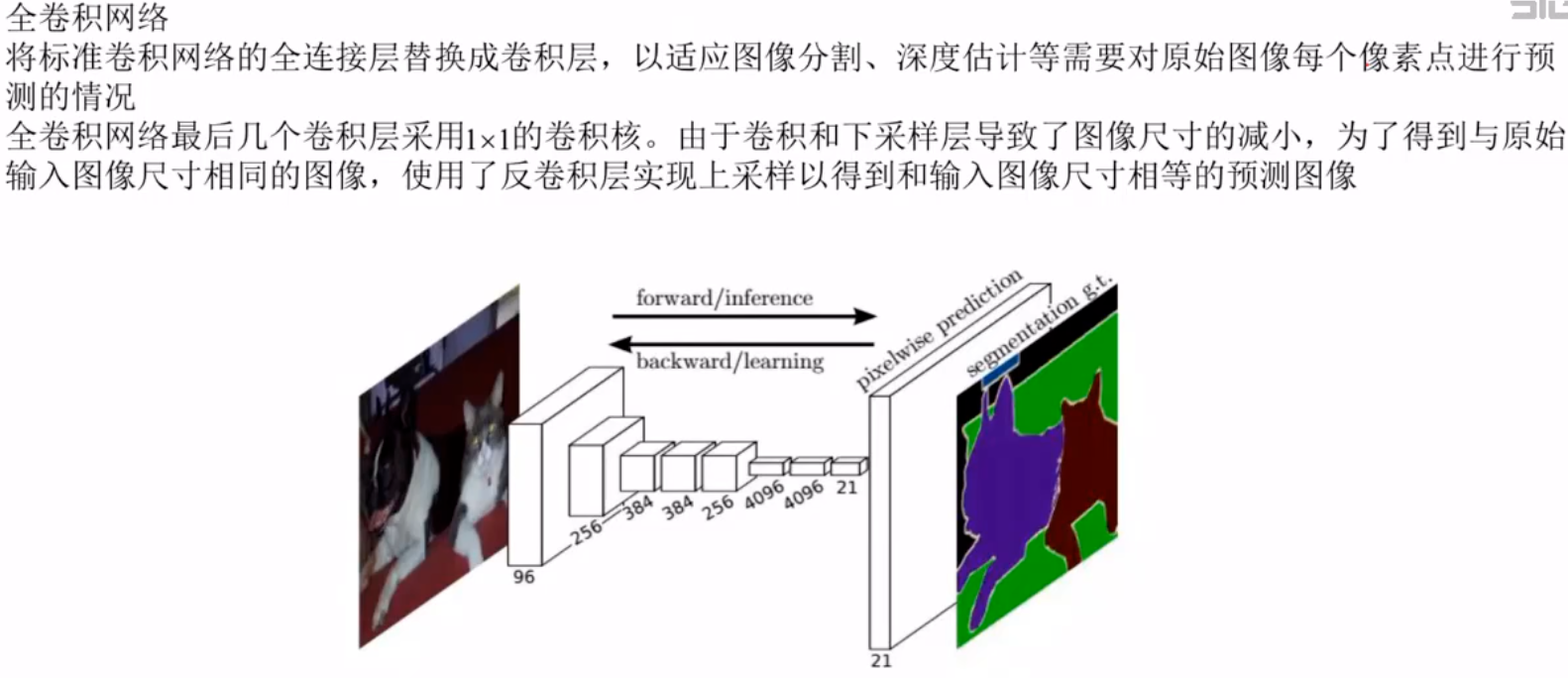
全卷积网络

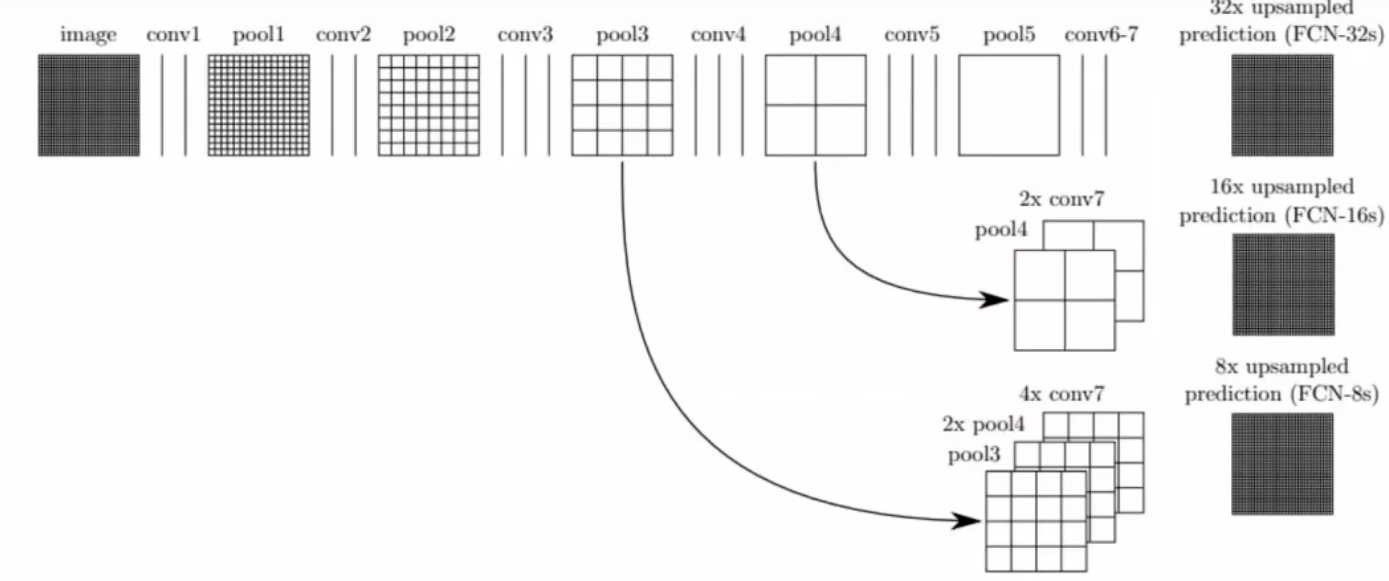
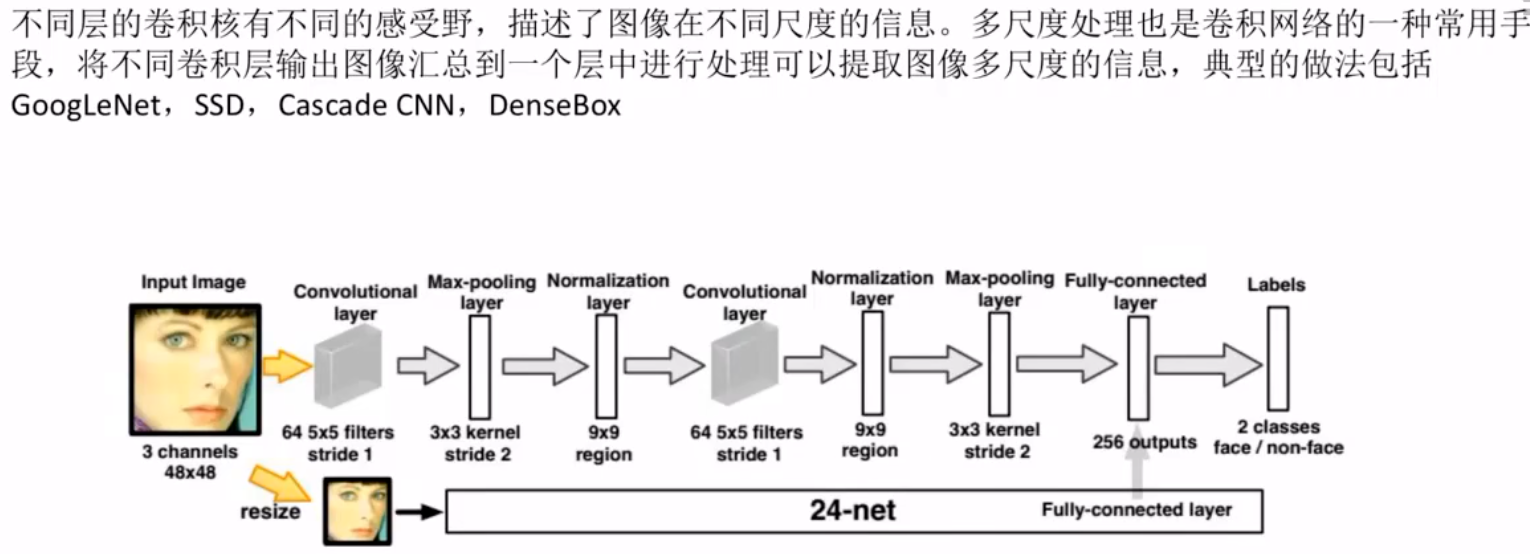
多尺度融合

批量归一化

总结：视频和这本书感觉关系不太大，这或许是和我是初学者有关。后续我会参考其他书籍进行进一步学习。

参考书籍：

《深度学习入门：基于Python的理论与实现》——（日）斋藤康毅 著；陆宇杰 译。

参考链接：

部分链接放在本文相应位置。

ANN,CNN,RNN,Attention,Encoder-Decoder,Tokenization梳理：神经网络算法：一文全面梳理ANN、CNN、RNN、Attention、Encoder-Decoder、Tokenization等必备知识点！ - 知乎

参考视频：

总览概括（先看该视频，对神经网络等有初步印象）：

https://www.bilibili.com/video/BV1NCgVzoEG9/?p=7&spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=0318931aabeaac5963b7db92a2c2bab5

这是本文的主要参考视频，以该视频为主制作：

https://www.bilibili.com/video/BV14kL2zNEdF?spm_id_from=333.788.player.switch&vd_source=0318931aabeaac5963b7db92a2c2bab5&p=55