机械臂时间最优规划

题目：Multi-objective optimal trajectory planning for robot manipulator attention to end-effector path limitation

机械臂的多目标最优轨迹规划关注末端执行器的路径限制

描述：在机械臂轨迹运动过程中，由于轨迹参数的调整，运动轨迹和预定轨迹不一致。无法满足特定任务的，即存在末端执行器路径的限制。本文提出基于前沿Pareo方法来解决这个问题，考虑机械臂多目标优化和末端执行器位置。在dung beetle优化器基础上提出一种非支配排序的dung beetle优化器。本文采用五次B样曲线插值，优化了行程时间、能量消耗、平均加速度的多目标轨迹优化，引入了Fréchet距离概念，提出一种基于Pareo的轨迹选择策略，该策略能够使实际轨迹逼近预定轨迹。仿真和实验结果验证了Sawyer机械臂的有效性和实用性。

介绍：关节空间规划、笛卡尔空间规划

在机械臂多目标轨迹优化中，优化对象通常是：时间-冲击、时间-能量、时间-能量-冲击

两种优化策略：

1. 加权的方法将多目标优化问题转化为单目标问题求解---需要设置合理的权重
2. 多目标优化算法：生成一组包含每个目标函数的最优解的

文章章节目录：

第二节：为什么采用五次B样条曲线采集--七自由度

第三节：改进的--非支配排序的dung beetle优化器--DBO算法

DBO算法--dung beetle优化器--非支配排序的dung beetle优化器

创新点1：原始的DBO算法采用的伪随机数来产生初始种群，去随机不彻底，优化采用PWLCM来生产均匀分布的初始种群 

图：

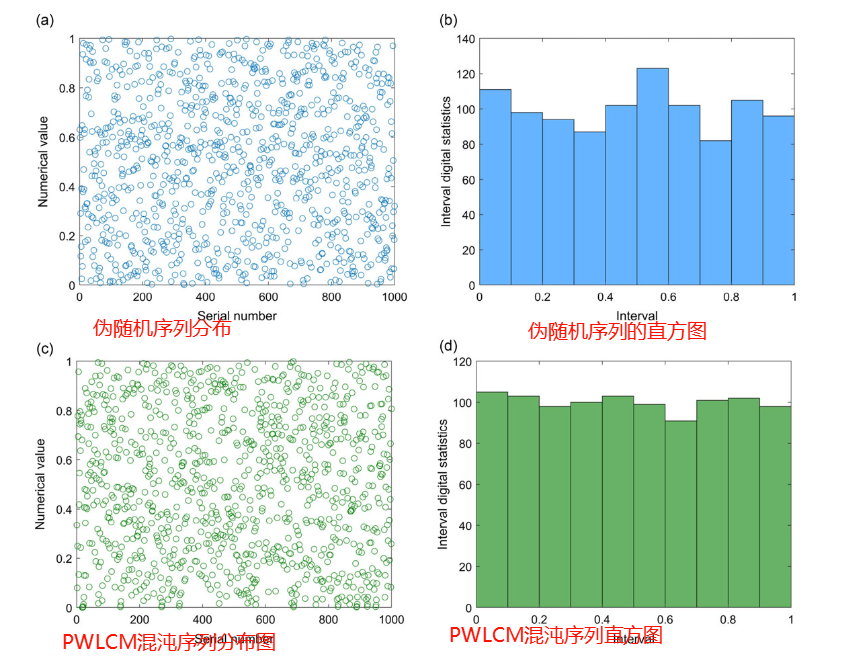
采用伪随机数和PWLCM序列两种方法生成( 0、1 )区间内的1000个随机数；然后，将区间划分为10个相等的子区间，并统计每个子区间内的随机数个数。图4给出了两种方法产生的随机数的位置和数量分布。从图4中可以看出，PWLCM序列的随机数在各个子区间内分布较为均匀。

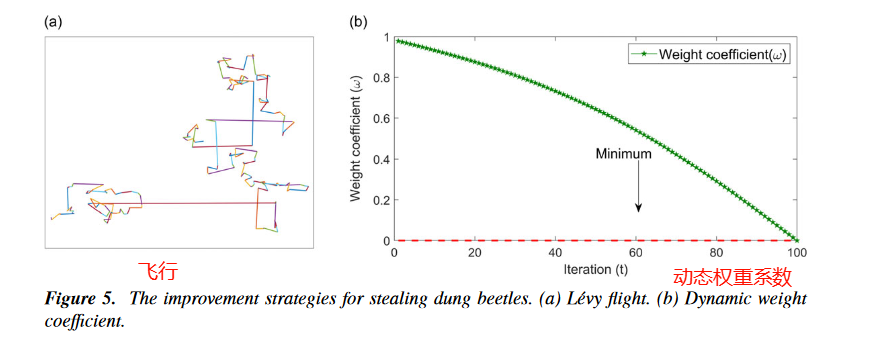
创新点2：Lévy飞行机制（布谷鸟也有）==算法的多样性

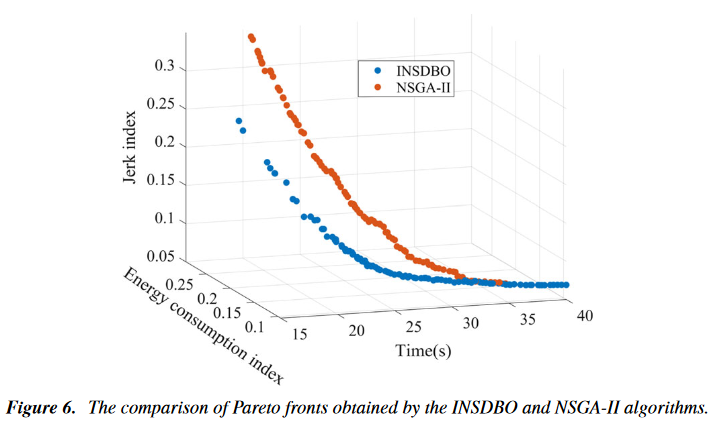
采用NSGA - II算法与INSDBO算法进行比较。

第四节：在Pareo解集中选择策略

第五节：仿真实验

第二节：