强化学习中的值迭代算法与实现
一、目标函数 Objective function
首先 vpis是对s的真的 state value vhat是他的一个估计值,我们的目标就是让vhat尽可能逼近,如果 vhat的结构是确定的时候,他是一个直线,抛物线,或者是神经网络拟合的黑箱,那么vhat(s,w),s确定了,我们可以调节的就是w,我们要做的就是找到一个最优的w,让这个vhat去接近vpi,这个问题实际上就变成了一个 policy的问题,我给了一个策略,我要找到一个近似的函数vhat,让他去接近真实的state value,之后也可以得到action value
1.1 目标函数的定义

目标函数 Jw,w是要优化的参数,他等于expection,后面跟着误差,误差是vpi是给定策略state value的真值,vhat是估计值的一个差的平方,我们的目标就是找到一个w,值得注意的是,这里的s是一个随机变量,随机变量就一定会有probablity distribution,那么这个平均与概率该怎么得到呢
1.1.1 uniform distribution 平均分布
假如我有n个状态,那么权重就是1/n

那么在这种情况下,目标函数求expection就能得到右边,所有的状态都在里面,但是正常情况我是要给离目标状态近的状态更大的权重,那么他们估计的误差会更小,这样我们就引入新的概率分布
1.1.2 stationary distribution
他描述了long-run behavior,我从一个状态出发,我按照一个策略,采取action,不断和环境交互,我一直采取这个策略,很多次之后,就知道每一个状态agent出现的概率是多少,我用dpi表示在每个s出现的概率,所以在每个s上概率大于等于0,和为1,那么

首先他是一个distribution,状态的概率分布,实际就是权重,而且为平稳,执行很多次之后达到的一个平稳
1.1.3 例子

现在我给了一个策略,因为每个action都有机会被选到,但是概率不同,所以这是一个探索性的策略,也有大的概率选择某个特定的action,让agent从一个地方出发,跑很多次,访问s的次数用n表示,那么npis除以访问所有状态的次数也就是episode的长度,得到的就是概率

这个上面是被访问到的状态次数,与访问总次数之比,s4的比值大,是因为他是最终状态,或者说他是里目标状态最近的一个,所以需要给他更大的权重,让他做对的选择,当然他也有个理论值,让我们可以不用很多次就可以得到值。
dpis满足这样一个式子
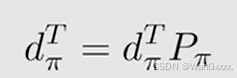
这里的Ppi就是状态转移矩阵,这里面的概率就是s到s`的概率

最后是可以计算出来,左边对应eigenvalue为1的eigenvector,这就对应了每个状态在平稳状态下的概率
1.2 目标函数的优化算法
想要对目标进行优化,很自然的就会想到梯度方法,找到下降的最低点

这个算法中,我们要优化的参数是w,后半的倒三角部分即为他的梯度,对于上面的式子,计算梯度的真实值,目标函数是均方误差的期望

设状态 S的分布与 w 无关(如策略固定时),则梯度算子 ∇w可与期望 E 交换顺序

下面根据链式法则,由于 vπ(S)是真实值(与 w 无关),其导数为零,故梯度作用于 v^(S,w):
![]()
将负号提到外层,最终形式为:
![]()
这样我们就得到了其真实的梯度,但是他需要计算一个expection,所以就用stochastic gradient 随机梯度 估计梯度来代替 ture gradient 真实梯度

为什么可以使用随机梯度来代替真实梯度?
1.2.1 随机梯度估计真实梯度的含义与原理
真实梯度(True Gradient): 在整个训练集上计算损失函数关于模型参数的梯度,即所有样本的平均梯度。例如,批量梯度下降(Batch Gradient Descent)中每次更新使用全部数据
随机梯度(Stochastic Gradient):通过单个样本或小批量样本(Mini-batch)估计的梯度。例如,随机梯度下降(SGD)每次随机选取一个样本计算梯度,小批量梯度下降则使用一小部分样本
随机梯度是真实梯度的无偏估计

上面替代的式子,这里面涉及了vpist,也就是当前策略在st处的state value,但是这个vpist就是我们需要求得的,所以不可以使用,但是可以用其他量来代替 vpist。我们就可以用蒙特卡洛的方法,用gt来代替
1.2.2 gt
首先,要理解episode的定义:在强化学习中,Episode(或称“回合”)指智能体(Agent)与环境(Environment)从初始状态开始交互,经过一系列动作(Action)、状态转移(State Transition)和奖励(Reward),最终到达终止状态的完整过程。一个 Episode 包含从初始状态 S0 到终止状态 ST 的所有动作和状态转移轨迹,即:
![]()
什么是gt?,从st出发有一个episode,沿着episode我有一系列的reward,得到的discounted return 就是gt,也就是对这个episode的评估,用gt做vpit的一个估值。

也可以用TD-Learning来代替Vpi(st)

1.3 select of function approximators
该式子表示一个线性值函数近似:

φ(s)是他的feature vector,手工设计的特征向量(如多项式、傅里叶基等),将状态 s 映射到高维特征空间。w是权重参数,
值函数V(s,w)是特征向量 ϕ(s)与权重 w 的线性组合,对权重 w 求偏导时,仅与对应特征分量相关,因此梯度直接等于特征向量 ϕ(s)。

如果用TD算法来表示

我需要选取合适的feature vectors,分析其理论性质
1.4 例子
接下来,我们给出了一些例子来说明如何使用的TD - Linear算法来估计给定策略的状态值。同时,我们演示了如何选择特征向量。
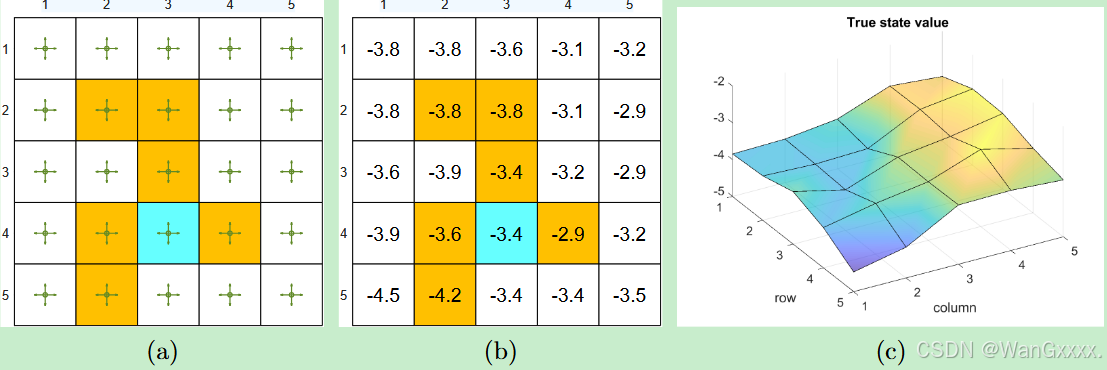
( a )待评估政策 ( b )真实状态值以表格的形式表示 ( c )将真实状态值表示为3D曲面。
网格世界的例子如图8.6所示。给定的政策在一个概率为0.2的状态下采取任何行动。我们的目标是估计该政策下的状态值。共有25个状态值。真实状态值如图8.6 ( b )所示。将真实状态值可视化为图8.6 ( c )中的三维曲面。
我们可以使用少于25个参数来近似这些状态值。仿真设置如下。五百集是由给定的政策产生的。每一集有500步,从一个随机选择的状态-动作对开始,服从均匀分布。此外,在每个模拟试验中,随机初始化参数向量w,使得每个元素从均值为零、标准差为1的标准正态分布中绘制。我们设定r禁戒= r边界= - 1,r目标= 1,γ = 0.9。
为了实现TD - Linear算法,首先需要选择特征向量φ ( s )。有不同的方法可以做到如下所示。第一类特征向量是基于多项式的。在网格世界的例子中,一个状态s对应一个2D位置。令x和y分别表示s的列指标和行指标.为了避免数值问题,我们将x和y归一化,使它们的值在[ - 1 , + 1]的范围内。在略微滥用记号的情况下,归一化值也用x和y表示。那么,最简单的特征向量就是

在这种情况下,我们有

为了增强逼近能力,可以增加特征向量的维数。

当我们使用( 8.16 )和( 8.17 )中的特征向量时的估计结果如图8.7 ( b ) - ( c )所示。可以看出,特征向量越长,越能准确地逼近状态值。然而,在所有三种情况下,估计误差都不能收敛到零,因为这些线性逼近器仍然具有有限的逼近能力。

二、Sarsa
先来看算法

和之前的TD算法是一模一样的,就是把v换成了q,之前是估计state value v^(st), 现在估计q^(st,at).这个算法实际上还是做一个 policy evaluation,给一个策略pi,估计出它的action value,相结合之后,就可以去搜索出最优策略

首先对每个episode做如下操作,如果当前状态st不是target state;在第一步,采取根据给定的策略采取行动,获得rt+1,st+1,之后在st+1再根据策略采取行动,然后给出value update。我们先更新了其w,做policy update。在st的时候采取action所对应的q value最大的action
三 Q-learning
先看算法

最大的区别就是加上了取最大值max,这个at是刚才at+1,下面给出伪代码

我从一个状态出发,找到一个目标状态的问题,如果当前的state不是traget state,在当前的状态st,根据策略pit得到了一个action at,然后得到rt+1与st+1,然后进行value update,更新其parameter,之后更新policy
四 DQN
想要设计一个神经网络,那么objective function / loss function就是必不可少的,而在这他的objective function对应的J(w)就是

这里面的式子实际上就对应了Bellman optimality error

如果想要进行优化,首先想到的还是梯度下降法
111
