机器学习日报13

摘要

今天学习了决策树处理不同类型特征的方法和回归树的应用。对于多值分类特征，使用独热编码将其转换为多个二元特征；对于连续值特征，通过寻找最佳分割阈值来划分数据。还了解了如何将决策树应用于回归问题，使用方差减少而不是信息增益来选择分割特征，并在叶节点预测数值平均值。

Abstract

Today’s study covered techniques for handling different feature types in decision trees and their extension to regression. One-hot encoding converts categorical features with multiple values into binary features. For continuous features, the algorithm finds optimal split thresholds. Regression trees use variance reduction instead of information gain for splits and predict average values at leaf nodes.

一、使用分类特征的一种独热编码（One - Hot）

目前我们的举得例子，每个特征只能取两个可能值之一，脸的形状圆或不圆，胡须或有或无，但是如果我们有特征可以取多于两个离散值，我们该怎么办呢，在本节中，我们将看看如何使用热编码来解决这样的问题

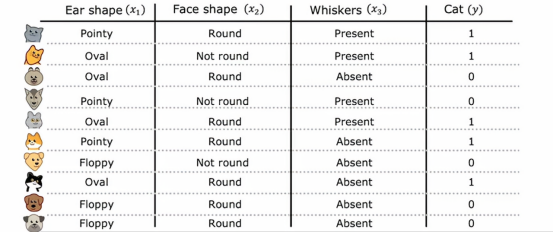
这是我们的宠物领养中心应用程序的新训练集，所有的数据都相同，除了耳朵形状特征耳朵的形状不仅仅是尖或垂，现在还可以是椭圆形，因此耳朵形状特征仍然是一个分类值特征，但它可以取三个可能的值，而不是只有两个，这意味着，当我们在这个特征上分裂数据时，我们会创建三个数据子集并最终为这棵树创建三个子分支，但在本节中，我们想学习的是一种不同的解决多值特征的方法，就是使用独热编码

具体来说，与其使用一个可以取三个可能值的耳朵形状特征，我们将创建三个新特征，其中一个特征是，这个动物是否有尖耳朵，第二个特征是是否有垂耳，第三个特征是是否有椭圆耳

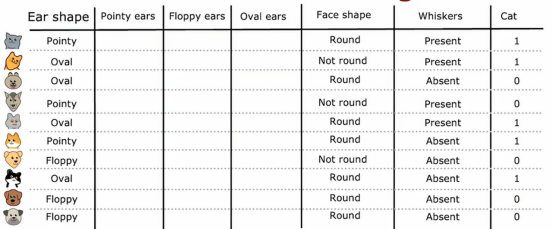
就拿第一个例子来看，我们可以看到这个猫的耳朵是尖耳，那么我们在尖耳的地方将其设置为1，然后再将垂耳和椭圆耳设置为0下面的例子也是同理

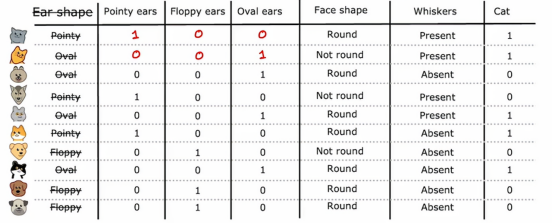
原来的情况是一个特征有3种情况，如果我们不好设计3棵子树，那么我们可以将其拆分为多个二元分类的特征，这样我们判断的范围依旧是0和1

广义来说，如果一个分类特征有K种可能值，在我们上面那个那个例子，k=3，那么这样我们就会创建k个二元特征来替换它，这些特征只能取0或1的值，我们可能会注意到这三个特征中，在任何一行里，都是恰好只有一个值等于1，这就是这种特征被称为独特编码的原因，因为这里分裂的特征中只会有一个是为1，因此得名独热编码，有了这种处理方法，我们就可以将复杂、多值的特征转变到每个只取两个可能值的简单特征，因此，我们以前见过的决策树学习算法可以直接应用到这些数据上，不需要进一步修改，顺便提一嘴，尽管我们的材料都集中在训练决策树模型上，使用独热编码来编码类别特征的想法同样适用于训练神经网络，特别是，如果我们将脸型特征中的圆形和非圆形用1和0替换，非圆形作为0，圆形作为1，把胡须也改成0和1的特征，现在这5个特征列表就可以输入到神经网络或逻辑回归中，尝试训练猫分类器，所以独热编码是一种不仅适用于决策树学习的技术，也让我们用1和0编码类别特征，这样也可以作为输入用于神经网络

就是这样通过独热编码，我们可以让决策树处理拥有超过两个离散值的特征，我们也可以将这种方法应用于神经网络，线性回归或逻辑回归，但是对于那种连续取值的数值特征呢，显然我们这节提到的方法就无法转化它们，这就引入我们下一个节的内容–连续的有价值特征

二、连续的有价值特征

让我们来看一下如何修改决策树以便处理不仅是离散值而是连续值的特征即那些可以取任意数值的特征

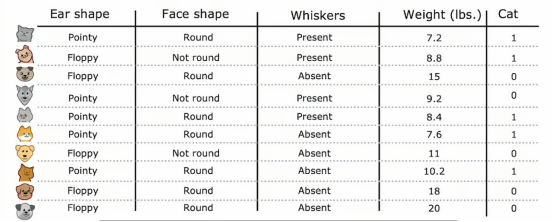
我们已经修改了猫咪收养中心的数据集，增加了一个特征，即动物的体重，平均而言，猫和狗之间，猫比狗轻一些，虽然有些猫比狗重一点，但是体重特征仍然可以决定它是否是猫的一个有用特征，那么如何让决策树使用这些特征呢决策树学习算法像之前一样进行，除了要考虑吧根据耳朵形状、脸型、胡须进行划分以外，还要考虑根据耳朵形状、脸型、胡须或体重进行划分，如果根据体重特征划分比其他选项提供更好的信息增益，那么你将根据体重特征进行划分，但我们如何决定如何根据体重特征划分呢，让我们来看一下，这是根节点数据的图示，我们口语在水平轴上绘制了动物的体重，垂直轴上方是猫，下方不是猫

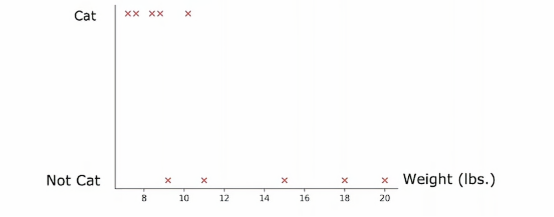
所以垂直轴表示标签y为1或者0，我们根据体重特征划分的方法是根据体重是否小于或等于某个值进行划分，比如说8或其他值，当考虑体重特征划分时，我们应该考虑许多不同的阈值，然后选择最优的那个，最优的意思是，产生最大信息增益的那个，特别地，如果我们考虑根据体重大小或小于等于8来划分

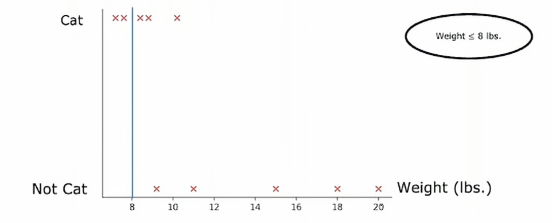
那么我们就将数据集划分为两个子集，左侧子集只有两个猫，右侧子集有三个猫和五只狗，所以如果我们计算通常的信息增益，我们将计算根节点的熵值

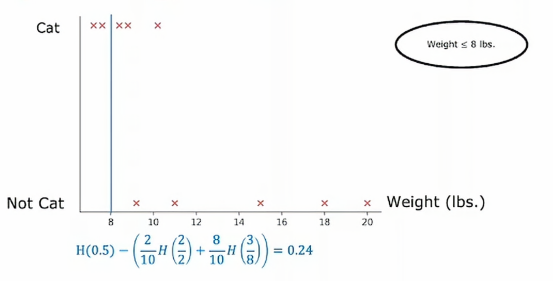
那么如果我们将阈值定为9呢，那么结果就是这样，顺便我们计算一下它的熵值

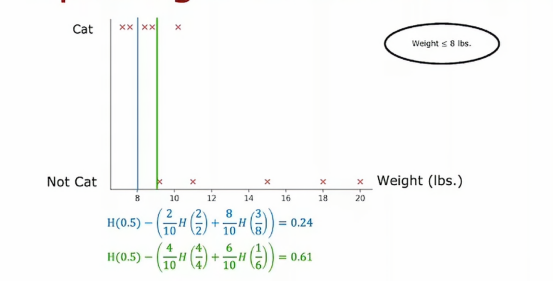
从数据上的表现来看，绿色比蓝色要好，那我们如果选择13当阈值呢，其结果如下

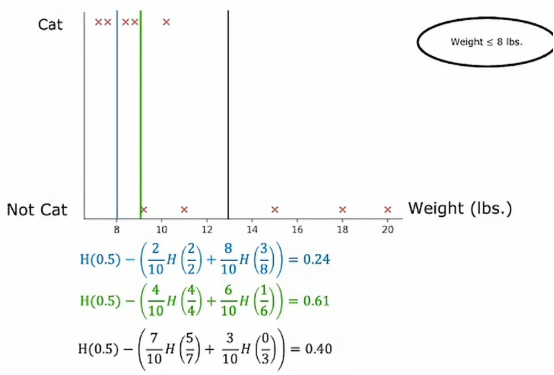
在更一般的情况下，我们肯定不只尝试3个值，而是沿着x轴尝试多个值，一种惯例是根据权重对所有样本进行排序，或者根据这个特征的值并取排序后训练样本中所有值的中点作为其值，然后尝试选择一个能给我们带来最大信息增益的值，用上面这个例子就是0.61，所以我们最终会根据动物的重量是否小于或等于9来分割数据集，这样我们就得到了这两个数据子集，然后我们可以递归地使用这两个数据子集构建额外的决策树来完成剩余的部分

三、回归树

到目前位置，我们只讨论了决策树作为分类算法的情况，在本节中，我们将把决策树泛化为回归算法，以便它们可以预测数值

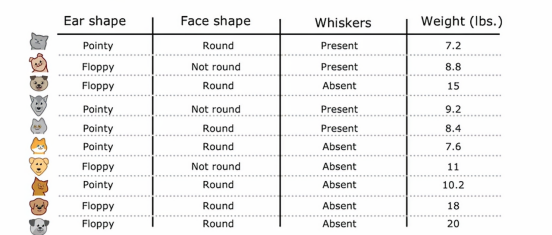
我们将在此视频中使用的例子是使用我们之前的离散值特征，我们需要明确的是，这里的重量不再是一个输入特征，而是一个输出标签y，而不是之前我们要预测的是否为猫这个目的，这是一个回归问题，因为我们想要预测一个数值y，让我们看看回归树会是什么样子

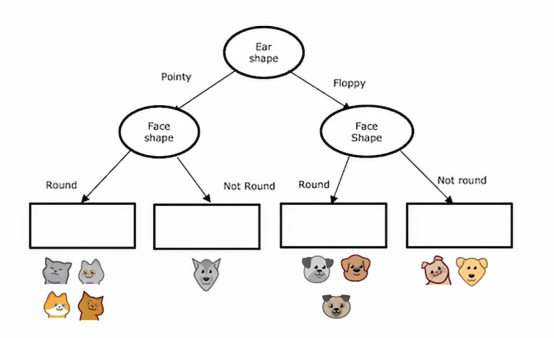
然后左子树和右子树依据脸型进行分裂，决策树在左右两边都选择同一特征进行分裂是没有问题的子树，如果在训练过程中，我们决定了那些分裂，那么这个节点下面就会有这些动物，它们的质量在下图

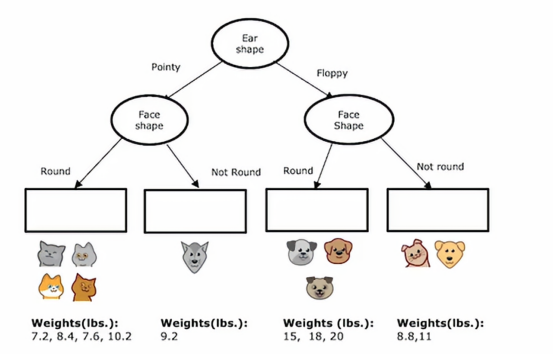
所以我们要为这决策树填写最后一件事是，如果有一个测试样本落到了这个节点，我们应该预测一个耳朵尖尖且脸圆的动物的重量是多少，决策树将基于这些训练样本中的权重平均值进行预测

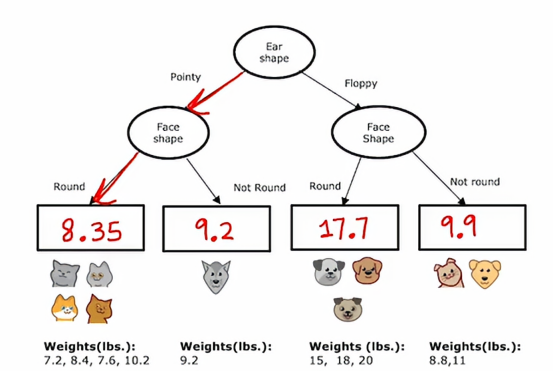
如果我们来个新的样本，按照惯例跟随决策节点直到下一个叶节点，然后在叶节点预测该值，这是我们通过计算这些动物体重的平均值得出的，在训练期间，到达同一个叶节点，如果我们从头构建一棵决策树，使用这个数据集来预测重量

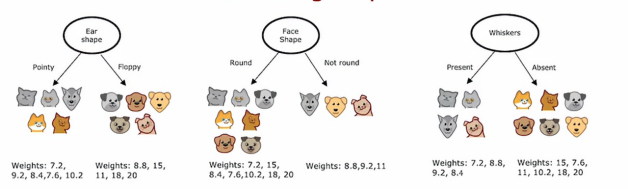
根我们之前的操作很类似，但是我们评判的标准变成了体重而已，在构建回归树时，我们不是试图减少熵，而是试图减少每个子集数据中的y值的体重方差

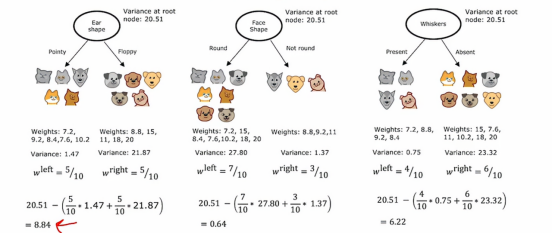
我们先计算每个分支的偏差，就如最左边的那棵来说，我们分别计算节点两边各自的方差，然后我们根据样本分布计算它们的权重然后再加起来，这样得到的平均方差是比较准确的，那么中间和右边也是同理

然后我们再计算根节点的方差，因为数据一开始是未分类的，所以我们得到的方差是一个数值，都是20.51，然后我们拿根节点的方差减去我们之前计算的平均方差，这样得出来的差值，意味着优化的程度，差值越大，优化效果越好，所以我们就可以选择左边的那个分类方法去构造回归树。

总结

今天的学习扩展了我对决策树应用范围的认识。独热编码很巧妙，能把一个多值特征变成几个二元特征，这样决策树和神经网络都能处理。连续特征的处理也很有启发性，通过尝试不同阈值找到最佳分割点。最让我意外的是决策树还能做回归任务，用方差减少代替信息增益，在叶节点预测平均值而不是类别。这些知识让我看到决策树确实是个很灵活的工具，既能分类又能回归，能处理各种类型的数据。