【BFS 解决最短路问题】3. 单词接⻰（hard）

3. 单词接⻰（hard）

题⽬链接：127. 单词接⻰

题⽬描述：

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是⼀个按下述规格形成的序列 beginWord -> s(1) -> s(2) -> … -> s(k) ：
• 每⼀对相邻的单词只差⼀个字⺟。
• 对于 1 <= i <= k 时，每个 s(i) 都在 wordList 中。注意， beginWord 不需要在 wordList中。
• s(k) = = endWord
给你两个单词 beginWord 和 endWord 和⼀个字典 wordList ，返回 从 beginWord 到endWord 的 最短转换序列 中的 单词数⽬ 。如果不存在这样的转换序列，返回 0 。
⽰例 1：
输⼊：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出：5
解释：⼀个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的⻓度 5。
⽰例 2：
输⼊：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出：0
解释：endWord “cog” 不在字典中，所以⽆法进⾏转换。
提⽰：
◦ 1 <= beginWord.length <= 10
◦ endWord.length = = beginWord.length
◦ 1 <= wordList.length <= 5000
◦ wordList[i].length = = beginWord.length
◦ beginWord 、 endWord 和 wordList[i] 由⼩写英⽂字⺟组成
◦ beginWord != endWord
◦ wordList 中的所有字符串 互不相同

解法：

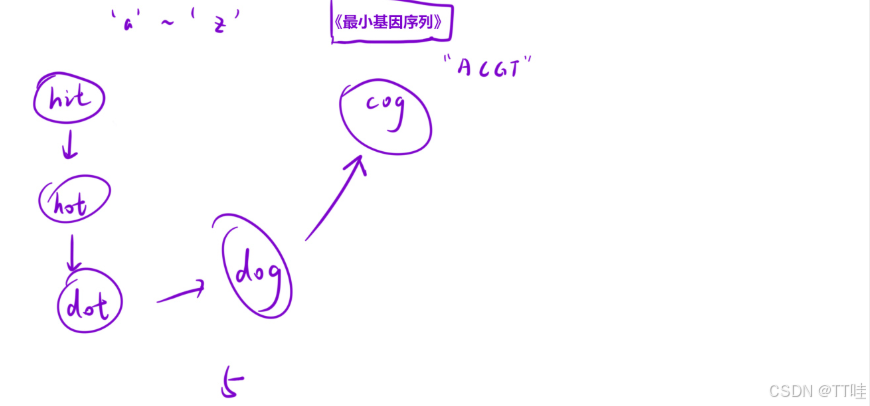
算法思路：

跟上题⼀样~2. 最⼩基因变化（medium）

算法代码：

class Solution
{public int ladderLength(String beginWord, String endWord, List<String> wordList) {Set<String> hash = new HashSet<>();for(String s : wordList) hash.add(s);Set<String> vis = new HashSet<>(); // 标记已经搜索过的单词if(!hash.contains(endWord)) return 0;Queue<String> q = new LinkedList<>();q.add(beginWord);vis.add(beginWord);int ret = 1;while(!q.isEmpty()){ret++;int sz = q.size();while(sz-- != 0){String t = q.poll();for(int i = 0; i < t.length(); i++){char[] tmp = t.toCharArray();for(char ch = 'a'; ch <= 'z'; ch++){tmp[i] = ch;String next = new String(tmp);if(hash.contains(next) && !vis.contains(next)){if(next.equals(endWord)) return ret;q.add(next);vis.add(next);}}}}}return 0;}
}