当前位置：首页 > news >正文

MIT-矩阵链相乘

news 2025/11/7 7:22:51

文章目录

问题描述
例子
算法实现
- 暴力枚举
- 动态规划

问题描述

假设你要计算矩阵乘积：

$A1A2A3⋯AnA_1A_2A_3\cdots A_n$

矩阵相乘虽然结合律成立（即 $A (BC) = (A B) C$ ）,但 乘法次数不同！

❗ 所以不同的加括号方式（计算顺序）会导致乘法次数差距极大。

例子

假设我们有三个矩阵：

$A_1$ 是 $10 \times 100$
$A_2$ 是 $100 \times 5$
$A_3$ 是 $\times 50$

1️⃣ $A_1A_2)A_3$

先算 $A_1A_2)$ ：需要 (10 × 100 × 5 = 5000) 次乘法
结果矩阵是 (10×5)
再算 $A_1A_2)A_3$ ：需要 (10 × 5 × 50 = 2500) 次乘法
总共：7500 次

2️⃣ $A_1(A_2A_3)$

先算 $A_2A_3)$ ：需要 (100 × 5 × 50 = 25000) 次乘法
结果矩阵是 (100×50)
再算 $A_1(A_2A_3)$ ：需要 (10 × 100 × 50 = 50000) 次乘法
总共：75000 次

🔥 差距是 10倍！
所以要找出“最优加括号方式”才能最省时间。

算法实现

暴力枚举

卡特兰数：设 $h (n)$ 为卡特兰数的第 $n$ 项，令 $h (0) = 1, h (1) = 1$ ，则卡特兰数满足递推式：

$h(n)=h(0)×h(n−1)+h(1)×h(n−2)+⋯+h(n−1)×h(0)=∑k=0n−1h(k)h(n−1−k)(n≥2)h(n)=h(0)\times h(n-1)+h(1)\times h(n-2)+\cdots+h(n-1)\times h(0)=\sum_{k=0}^{n-1}h(k)h(n-1-k)(n\geq2)$

即 $h(n)=C2nnn+1(n∈N)h(n)=\frac{C_{2n}^n}{n+1}(n\in N)$ 。

$n$	$h (n)$
0	1
1	1
2	2
3	5
4	14

我们定义 $f (n)$ 为 $n$ 个矩阵相乘时不同的加括号方式数目。
例如：

$f (1) = 1$ ：一个矩阵不需要括号；
$f (2) = 1$ ：两个矩阵只有一种乘法方式；
$f (3) = 2$ ：三矩阵可以是 $A_1A_2)A_3$ 或 $A_1(A_2A_3)$ 。

故有：

$f(n)=∑k=1n−1f(k)f(n−k)f(n)=\sum_{k=1}^{n-1}f(k)f(n-k)$

把 $n$ 个矩阵分成两部分：
$(A1A2⋯Ak)(Ak+1Ak+2⋯An)(A_1A_2\cdots A_k)\left(A_{k+1}A_{k+2}\cdots A_n\right)$
前面那部分的加括号方式有 $f (k)$ 种；
后面那部分有 $f (n - k)$ 种；
这两部分组合起来就是 $\times f(n-k)$ 种；
最后对所有可能的 $k$ 求和。

$n$	$f (n)$
1	1
2	1
3	2
4	5
5	14

观察可知

$f (n) = h (n - 1)$

也就是说 $f$ 比卡特兰数 $h$ 的下标大 1。

所以

$f(n)=C2n−2n−1n=(2n−2)!n((n−1)!)2f(n)=\frac{C_{2n-2}^{n-1}}{n}=\frac{(2n-2)!}{n((n-1)!)^2}$

其中 $n!$ 可近似为：

$n!≈2πn(ne)nn!\approx\sqrt{2\pi n}\left(\frac{n}{e}\right)^n$

故

$(2n−2)!≈2π(2n−2)(2n−2e)2n−2=22n−1π(n−1)(n−1e)2n−2(2n-2)!\approx\sqrt{2\pi (2n-2)}\left(\frac{2n-2}{e}\right)^{2n-2}=2^{2n-1}\sqrt{\pi(n-1)}(\frac{n-1}{e})^{2n-2}$
$(n−1)!≈2π(n−1)(n−1e)n−1=20.5π(n−1)(n−1e)n−1(n-1)!\approx\sqrt{2\pi (n-1)}\left(\frac{n-1}{e}\right)^{n-1}=2^{0.5}\sqrt{\pi(n-1)}(\frac{n-1}{e})^{n-1}$

$f(n)=(2n−2)!n((n−1)!)2≈22n−2nπ(n−1)≈4n4n1.5πf(n)=\frac{(2n-2)!}{n((n-1)!)^2}\approx \frac{2^{2n-2}}{n\sqrt{\pi(n-1)}}\approx\frac{4^n}{4n^{1.5}\sqrt{\pi}}$

故 $f(n)=O(4nn1.5)f(n)=O(\frac{4^n}{n^{1.5}})$

这是一个极其庞大的数！一个一个枚举显然不合适！

动态规划

维度数组： $p_0$ 是第一个矩阵的行数， $p_1$ 是第一个矩阵的列数，第二个矩阵的行数。

$p=[p0,p1,p2,…,pn]p=[p_0,p_1,p_2,\ldots,p_n]$

$A_1$ 矩阵的维数是 $p0×p1p_0\times p_1$ ， $A_1A_2$ 矩阵的维数是 $p0×p2p_0\times p_2$ ， $A_2A_3$ 矩阵的维数是 $p1×p3p_1\times p_3$ ，… ， $A1…AnA_1\ldots A_n$ 矩阵的维数是 $p0×pnp_0\times p_n$ 。
$A_1(A_2A_3)$ 所需的计算次数为 $p0×p1×p3p_0\times p_1 \times p_3$

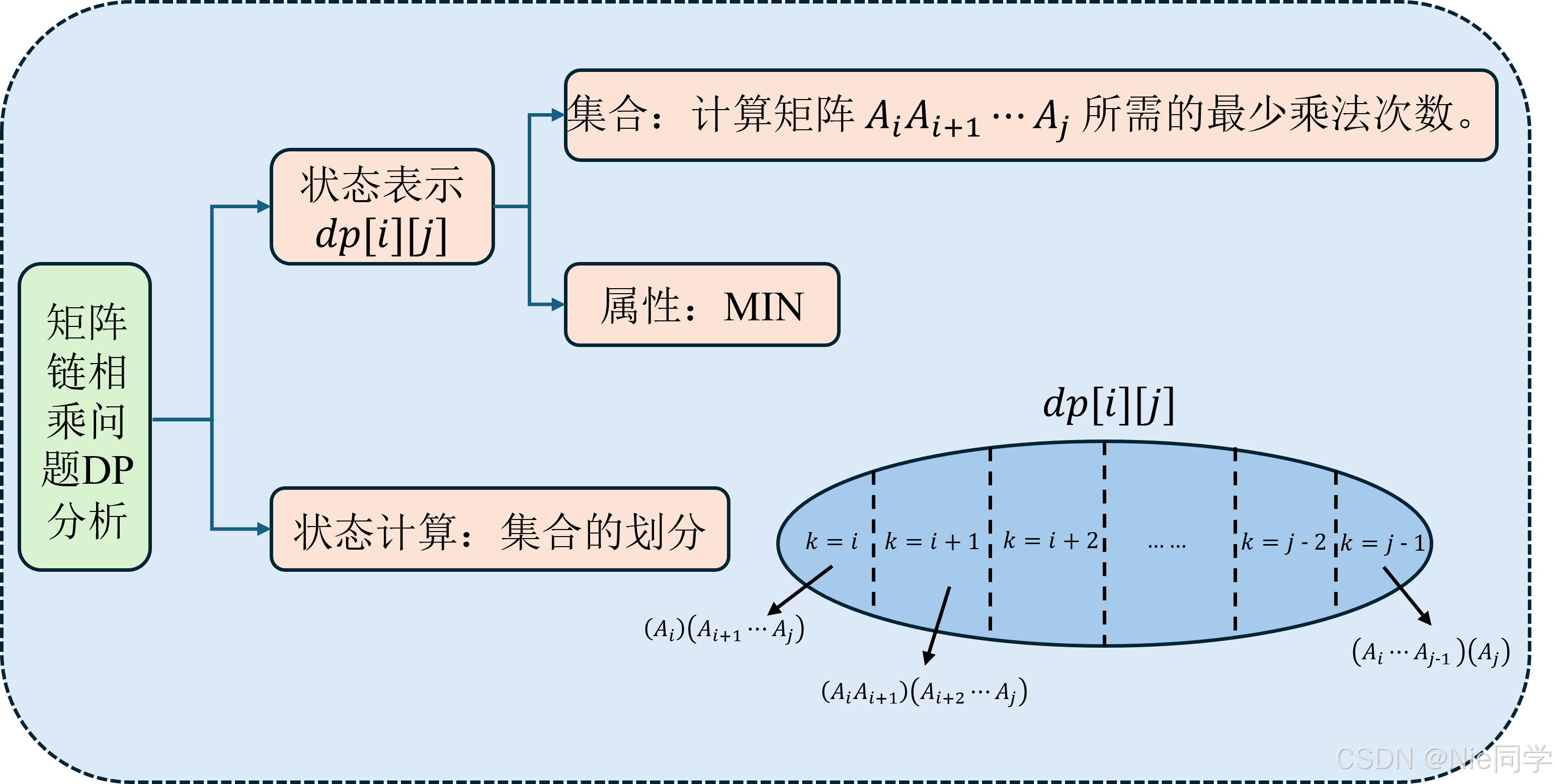
状态定义： 此时我们定义 $d p [i] [j]$ 是计算矩阵 $AiAi+1⋯AjA_iA_{i+1}\cdots A_j$ 所需的最少乘法次数。

初始化： 当 $d p [i] [j]$ 中的 $i == j$ 时，表示一个矩阵所需的最少乘法次数，即 $d p [i] [i] = 0$ 。

转移方程： 如果在第 $k(i≤k<j)k(i\leq k< j)$ 处分割：

则：

$d p [i] [j] = min (d p [i] [j], d p [i] [k] + d p [k + 1] [j] + p [i - 1] p [k] p [j])$

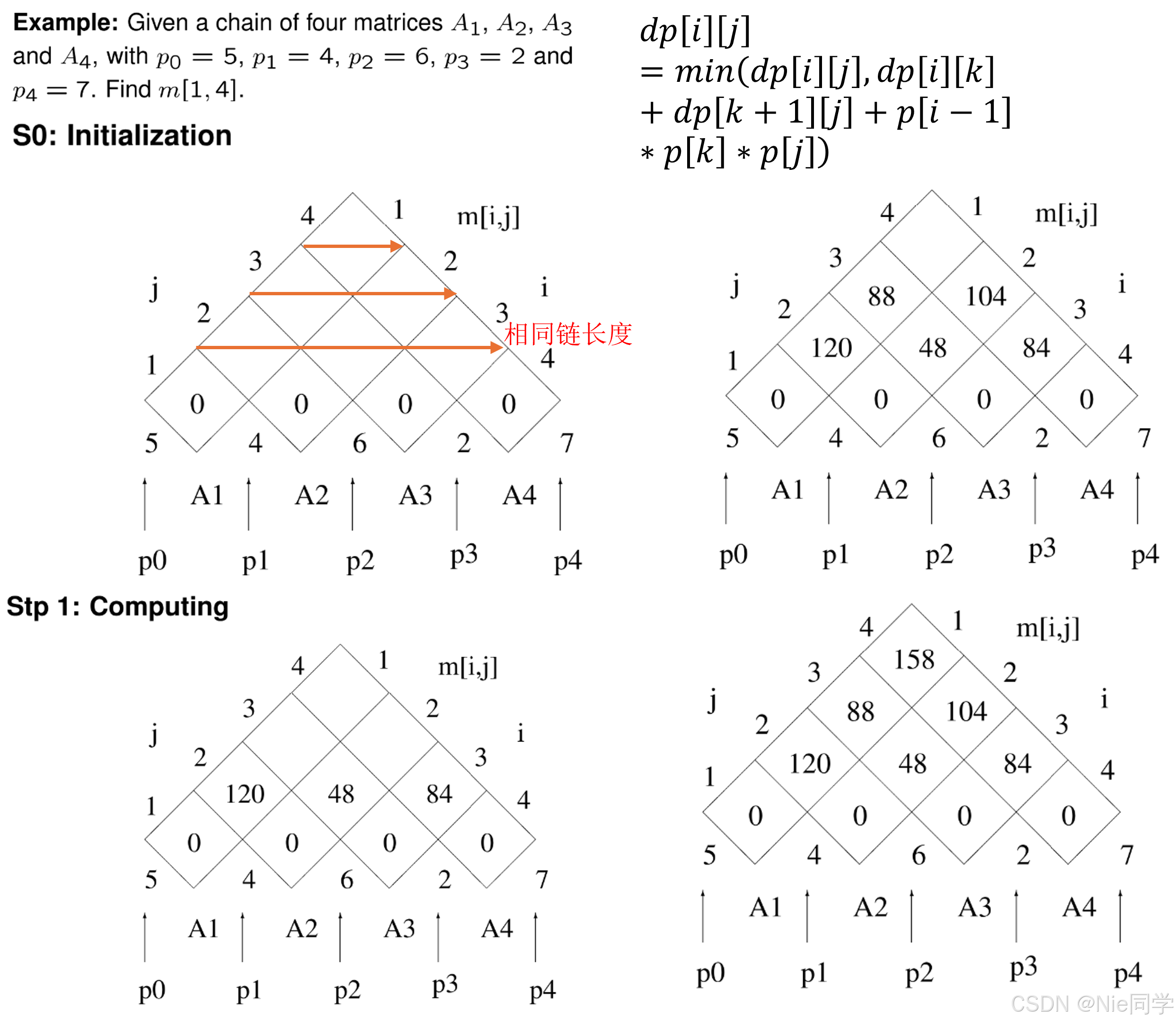
请添加图片描述

int DPmatrixChain(int p[], int n)
{int dp[n + 1][n + 1];/* 初始化操作 */for (int i = 1; i <= n; i ++ ) dp[i][i] = 0;/* 错误操作for (int i = 1; i <= n; i ++ ) 这样的循环会出现所用到更小的子问题，并没有出现在表中for (int j = i + 1; j <= n; j ++ )for (int k = i; k < j; k ++ )dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] *  p[j]);  dp[i][j] 依赖于比它“短”的子区间的值*//* 正确操作：当我要求解一个子问题时，它所依赖的更小子问题的结果已经在表中 */for (int len = 2; len <= n; len ++ )for (int i = 1; i <= n - len + 1; i ++ ){int j = i + len - 1;dp[i][j] = INT_MAX;for (int k = i; k < j; k ++ )      // 枚举分割点dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j]);}return dp[1][n];
}