当前位置：首页 > news >正文

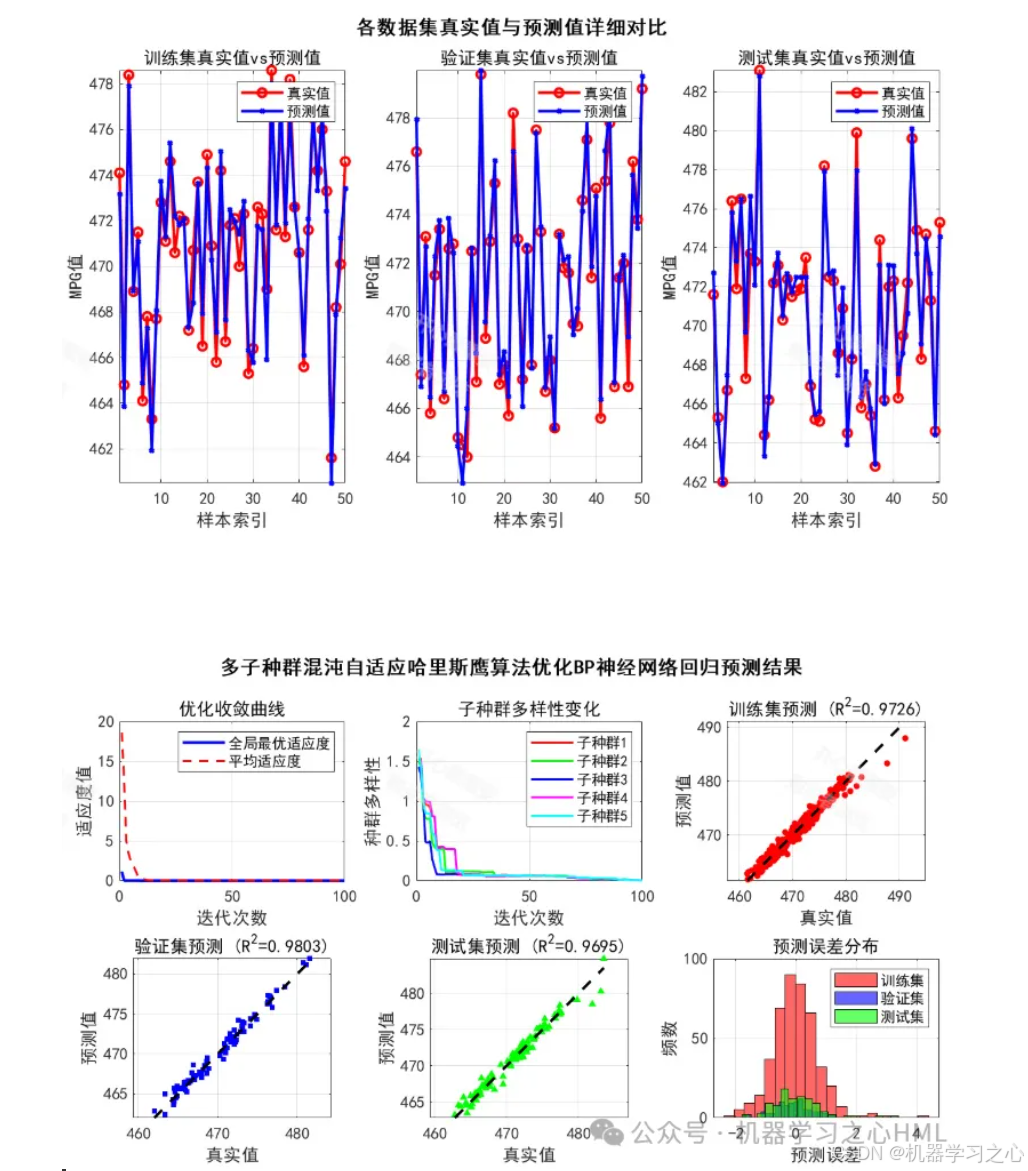
MATLAB多子种群混沌自适应哈里斯鹰算法优化BP神经网络回归预测

news 2025/11/6 12:26:42

整体思想：为什么要用MSCAHHO优化BP神经网络？

BP神经网络的痛点：

对初始权重和阈值敏感：随机初始化容易使网络陷入局部最优解。
梯度消失/爆炸：在误差反向传播过程中，梯度可能变得极小或极大，导致训练缓慢或不收敛。
收敛速度慢：需要多次迭代和精细调整学习率。

MSCAHHO的解决方案：
哈里斯鹰算法（HHO）是一种强大的全局优化算法，模拟鹰群的协作捕食行为。通过引入多子种群、混沌初始化和自适应机制，MSCAHHO对基础HHO进行了增强，使其更适用于复杂、高维的神经网络参数优化问题。

核心思想是：将BP神经网络的权重和阈值编码为哈里斯鹰的位置向量。MSCAHHO的任务就是在解空间中寻找一组最优的位置（即网络参数），使得网络的预测输出与真实值之间的误差（如均方误差MSE）最小。

模型组成部分详解

1. BP神经网络回归预测模型

结构：典型的输入层-隐藏层-输出层结构。
任务：回归预测，即学习一个从输入特征到连续输出值的复杂映射函数。
待优化参数：所有连接层的权重（Weights） 和神经元的阈值（Biases）。这些参数共同构成了一个高维的解空间。

2. 多子种群混沌自适应哈里斯鹰算法（MSCAHHO）

这是在标准HHO基础上的三重增强：

a) 混沌初始化（Chaotic Initialization）

目的：改善初始种群的多样性和分布质量，避免早熟收敛。
方法：使用混沌映射（如Logistic Map、Tent Map）来生成初始鹰群的位置，代替纯粹的随机生成。这能使鹰群更均匀地覆盖整个搜索空间，为全局搜索打下良好基础。

b) 多子种群策略（Multi-Subpopulation Strategy）

目的：平衡算法的探索（全局搜索） 和开发（局部挖掘） 能力。
方法：将整个鹰群划分为多个子种群，例如：
- 探索者子群：专注于在全局范围内寻找新的有希望的区域。
- 开发者子群：专注于在已知的优秀区域进行精细搜索。
- 跟随者或侦察子群：负责在算法陷入停滞时进行随机侦察，跳出局部最优。
机制：不同子群采用不同的位置更新策略，并定期进行信息交流（如个体迁移），实现协同进化。

c) 自适应机制（Adaptive Mechanism）

目的：动态调整算法参数，使其在搜索初期偏向探索，后期偏向开发。
核心参数：HHO中的猎物逃逸能量（E）。
- 在标准HHO中，E从2线性下降到0。
- 在MSCAHHO中，E的下降可以是非线性的、自适应的。例如，根据当前种群的收敛程度或多样性来自适应地调整E的值。当种群多样性高时，保持较大的E以鼓励探索；当陷入局部最优时，扰动E值以帮助跳出。

MSCAHHO优化BP神经网络的实现步骤

该流程是一个完整的闭环优化系统，其核心步骤如下图所示：

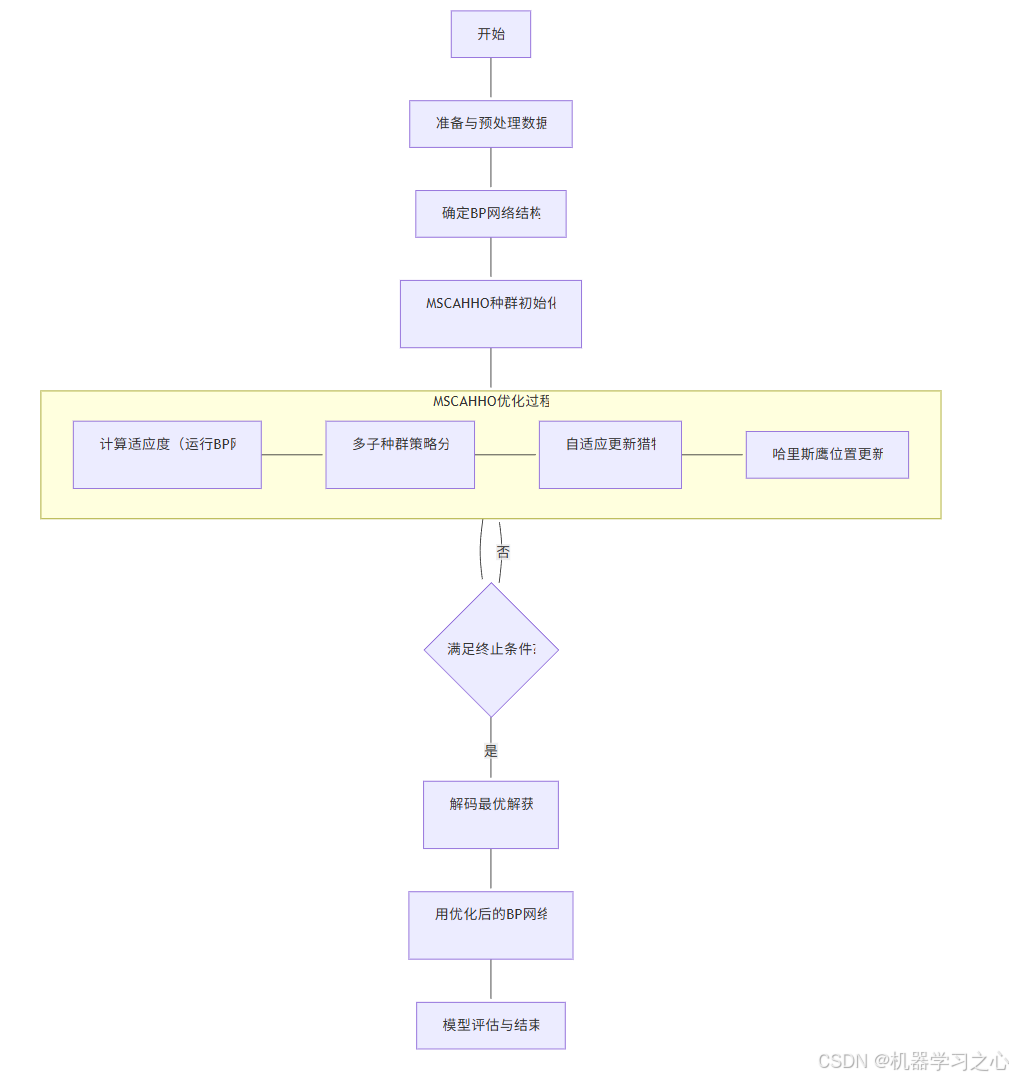
在这里插入图片描述

步骤概览：

数据准备与预处理：收集回归预测数据，进行归一化，并划分为训练集和测试集。
确定BP网络结构：设定输入层、隐藏层神经元数、输出层神经元数。
参数编码：将BP网络的所有权重和阈值编码成一个一维向量，作为一只“哈里斯鹰”的位置。向量的维度 = (输入层数 * 隐藏层数) + (隐藏层数 * 输出层数) + 隐藏层数 + 输出层数。
MSCAHHO初始化：
- 设定鹰群大小、最大迭代次数、子种群划分方式等。
- 使用混沌映射初始化所有鹰（即所有网络参数组）的位置。
MSCAHHO主循环：
- 计算适应度：对每一只鹰（每一组参数），将其解码并赋给BP网络。在训练集上运行网络前向传播，计算预测值与真实值的均方误差（MSE） 作为适应度函数。MSE越小，适应度越高。
- 多子种群操作：根据适应度或预设规则，将鹰群划分为不同子群。各子群按照其角色（探索/开发）使用HHO的四种捕食策略（软包围、硬包围、渐进式快速俯冲、突袭）进行位置更新。
- 自适应更新：根据当前迭代进度和种群状态，自适应地更新猎物逃逸能量E。
- 判断终止：检查是否达到最大迭代次数或满足精度要求。
输出最优解：循环结束后，输出全局最优的鹰的位置向量。
构建最终预测模型：将MSCAHHO找到的最优位置向量解码，作为BP神经网络的最终权重和阈值。
预测与评估：使用优化好的BP网络，在测试集上进行预测，并评估其泛化性能（如使用R², MAE, RMSE等指标）。