MIT-0-1背包问题
文章目录
- 问题描述
- 例子
- 算法实现
问题描述
有 NNN 件物品和一个容量是 VVV 的背包。每件物品只能使用一次。第 iii 件物品的体积是 wiw_iwi,价值是 viv_ivi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
例子
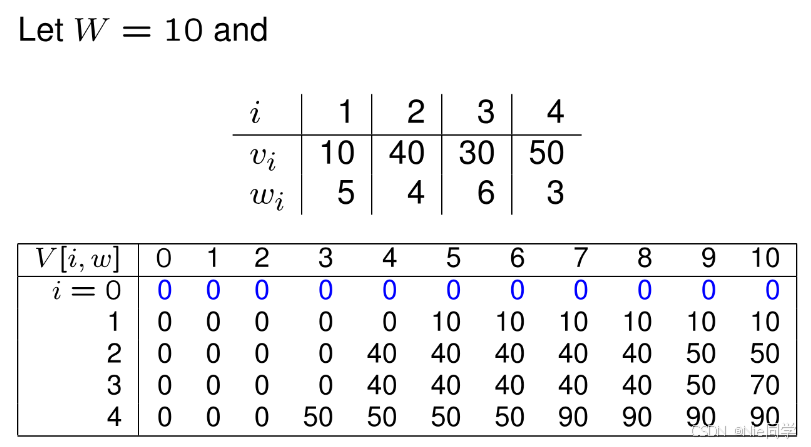
算法实现
动态规划是不断决策求最优解的过程,0-1 背包即是不断对第 iii 个物品的做出决策,0-1代表不选与选两种决定。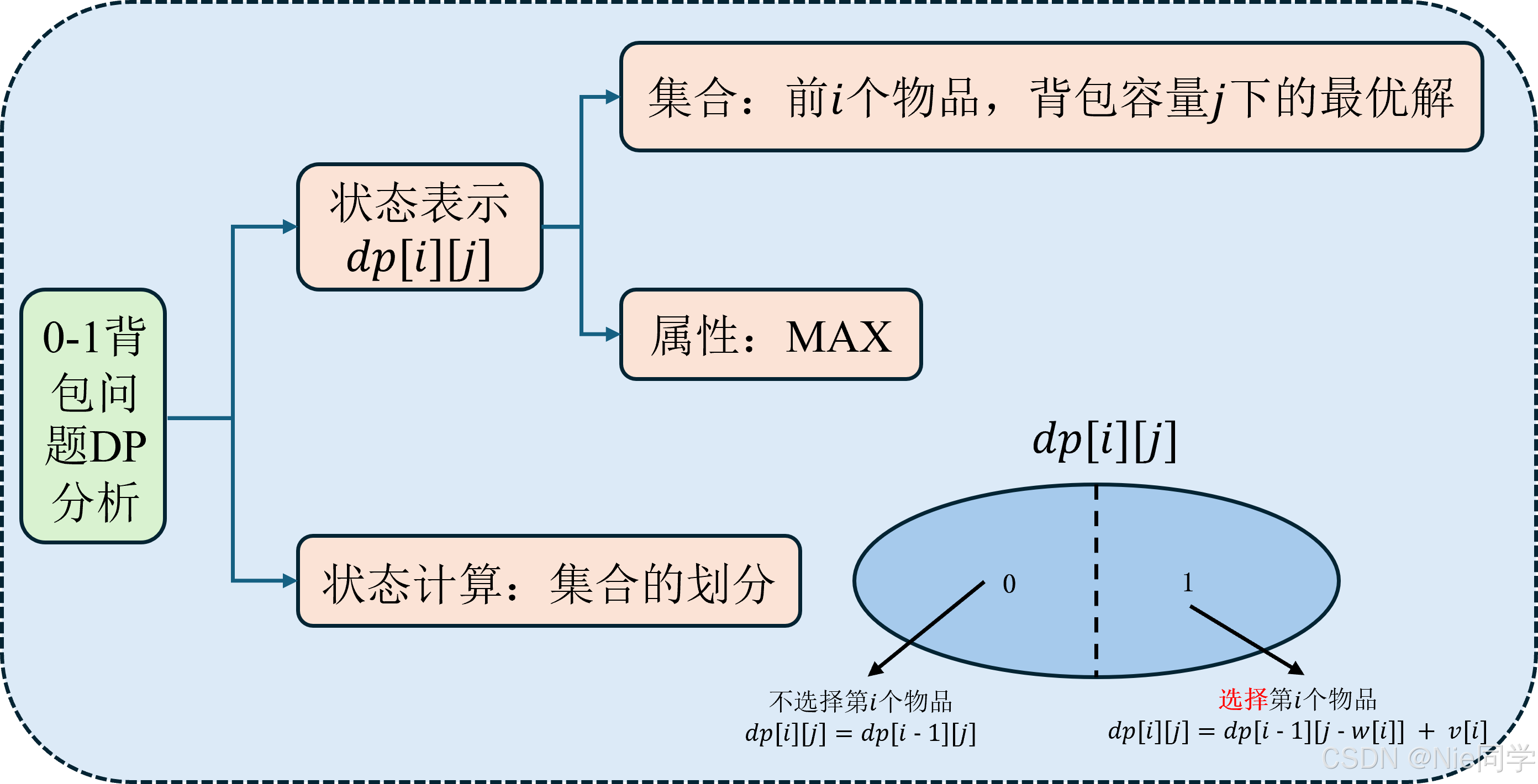
- 初始化:dp[0][i]=dp[i][0]=0dp[0][i]=dp[i][0]=0dp[0][i]=dp[i][0]=0
- 当前背包容量不够 j<w[i]j<w[i]j<w[i],没得选,dp[i][j]=dp[i−1][j]dp[i][j]=dp[i-1][j]dp[i][j]=dp[i−1][j]
- 当前背包容量够 j≥w[i]j\geq w[i]j≥w[i]:
- 选:dp[i][j]=dp[i−1][j−w[i]]+v[i]dp[i][j]=dp[i-1][j-w[i]]+v[i]dp[i][j]=dp[i−1][j−w[i]]+v[i]:前 i−1i-1i−1 个物品,背包容量为 jjj 下,空出第 iii 个元素所需要的空间的最优解,然后再加上第 iii个物品的价值,即是前 iii 个物品,背包容量为 jjj 下的最优解。
- 不选:dp[i][j]=dp[i−1][j]dp[i][j]=dp[i-1][j]dp[i][j]=dp[i−1][j]
int dp[n][m];
int w[n], v[n];/* 初始化 */
for (int i = 0; i <= m; i ++ ) dp[0][i] = 0;for (int i = 0; i <= n; i ++ ) dp[i][0] = 0;/* 动态规划 */
for (int i = 1; i <= n; i ++ )
{for (int j = 1; j <= m; j ++ ){if (j < w[i]) // 当前背包容量不够,没得选,dp[i][j]=dp[i-1][j]dp[i][j] = dp[i - 1][j];else // 当前背包容量够dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])}
}return dp[n][m];
时间复杂度:O(nm)O(nm)O(nm)
