用Python来学微积分31-定积分的概念与几何意义详解
文章目录
- 一、定积分的基本思想:从面积问题说起
- 二、定积分的精确定义
- 2.1 黎曼和的构造过程
- 2.2 定积分的各部分名称
- 2.3 定积分的基本性质
- 三、定积分的几何意义
- 3.1 非负函数的几何意义
- 3.2 一般情况的几何意义
- 四、定积分概念的实际应用
- 4.1 物理应用:变速直线运动的路程
- 4.2 经济应用:总成本计算
- 总结
一、定积分的基本思想:从面积问题说起
定积分的核心思想源于计算曲边梯形面积的实际需求。当我们面对一个由任意曲线 y=f(x)y = f(x)y=f(x) 构成的图形时,无法直接用简单的几何公式计算其面积,这就需要一种新的数学工具。
核心思路:采用"分割-近似-求和-取极限"的方法。具体来说,就是将曲边梯形分割成许多细长的矩形,用这些矩形面积的和来近似曲边梯形的面积。当分割越来越细时,近似值就会越来越精确,其极限值就是曲边梯形的精确面积。
下面通过Python代码可视化这一过程:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangledef visualize_riemann(f, a, b, n=10):"""可视化黎曼和逼近曲边梯形面积的过程"""x = np.linspace(a, b, 1000)y = f(x)fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))# 左图:函数曲线和分割示意ax1.plot(x, y, 'b-', linewidth=2, label='y = f(x)')ax1.set_xlabel('x')ax1.set_ylabel('y')ax1.set_title('曲边梯形示意图')ax1.grid(True, alpha=0.3)ax1.legend()# 右图:黎曼和可视化x_divisions = np.linspace(a, b, n+1)ax2.plot(x, y, 'b-', linewidth=2, label='y = f(x)')# 计算中点黎曼和riemann_sum = 0for i in range(n):x_left = x_divisions[i]x_right = x_divisions[i+1]x_mid = (x_left + x_right) / 2y_mid = f(x_mid)width = x_right - x_left# 添加矩形rect = Rectangle((x_left, 0), width, y_mid, alpha=0.3, color='red')ax2.add_patch(rect)riemann_sum += y_mid * widthax2.set_xlabel('x')ax2.set_ylabel('y')ax2.set_title(f'黎曼和逼近 (n={n}, 面积近似值: {riemann_sum:.4f})')ax2.grid(True, alpha=0.3)ax2.legend()plt.tight_layout()plt.show()return riemann_sum# 示例:计算 y = x² 在 [0, 1] 上的积分
def f_example(x):return x**2# 可视化不同分割精细度的逼近效果
for n in [5, 10, 20]:approximate_area = visualize_riemann(f_example, 0, 1, n)theoretical_area = 1/3print(f"n={n}: 近似面积={approximate_area:.4f}, 误差={abs(approximate_area - theoretical_area):.4f}")
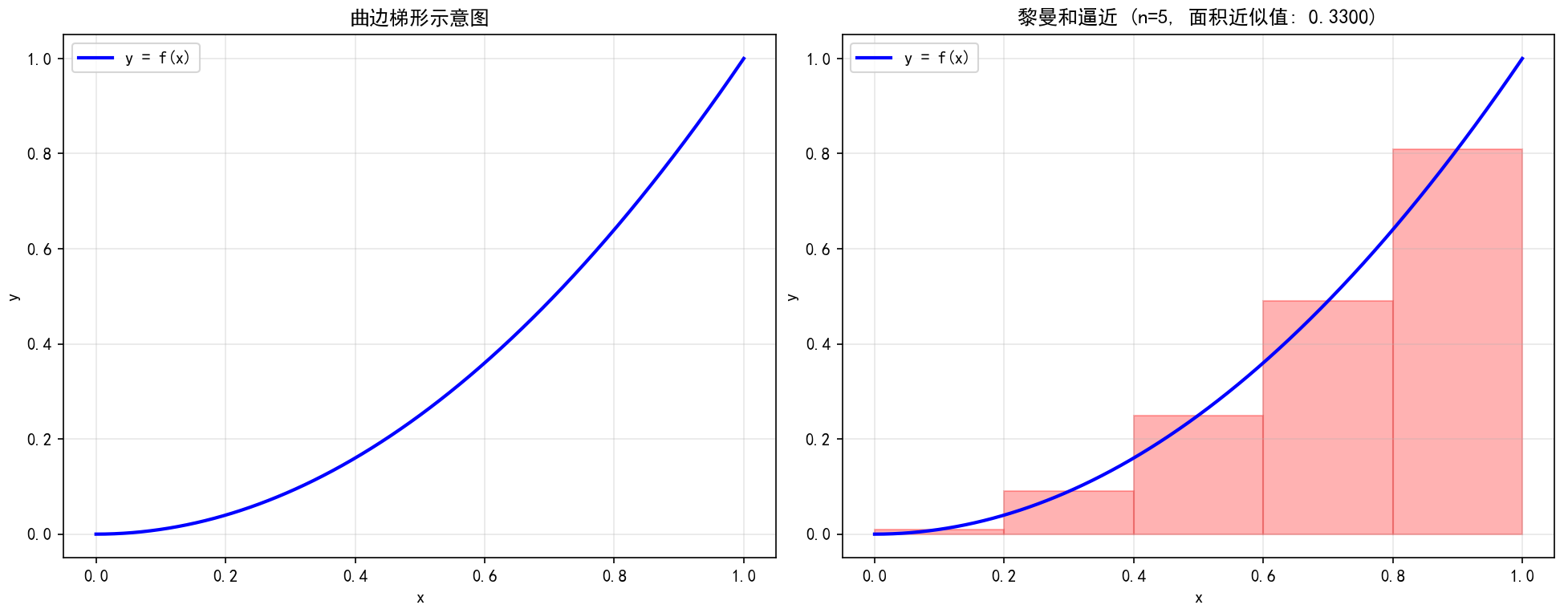
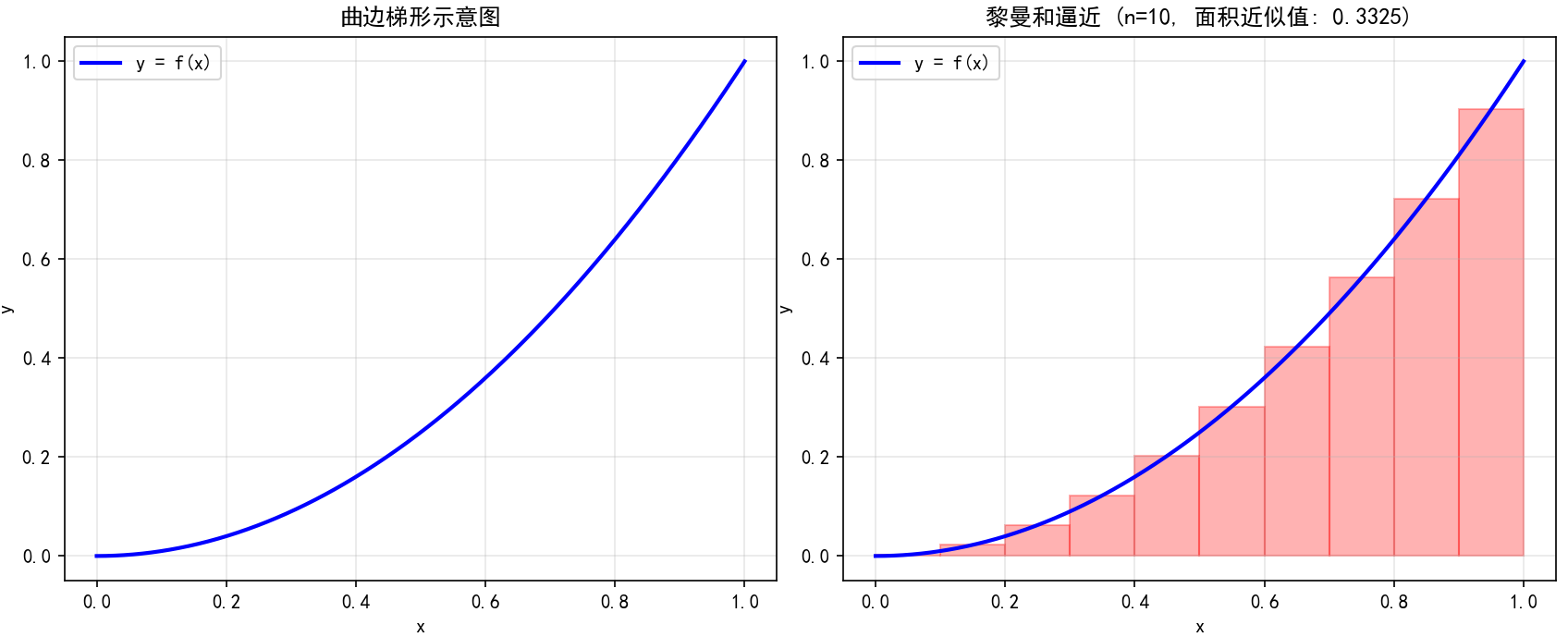
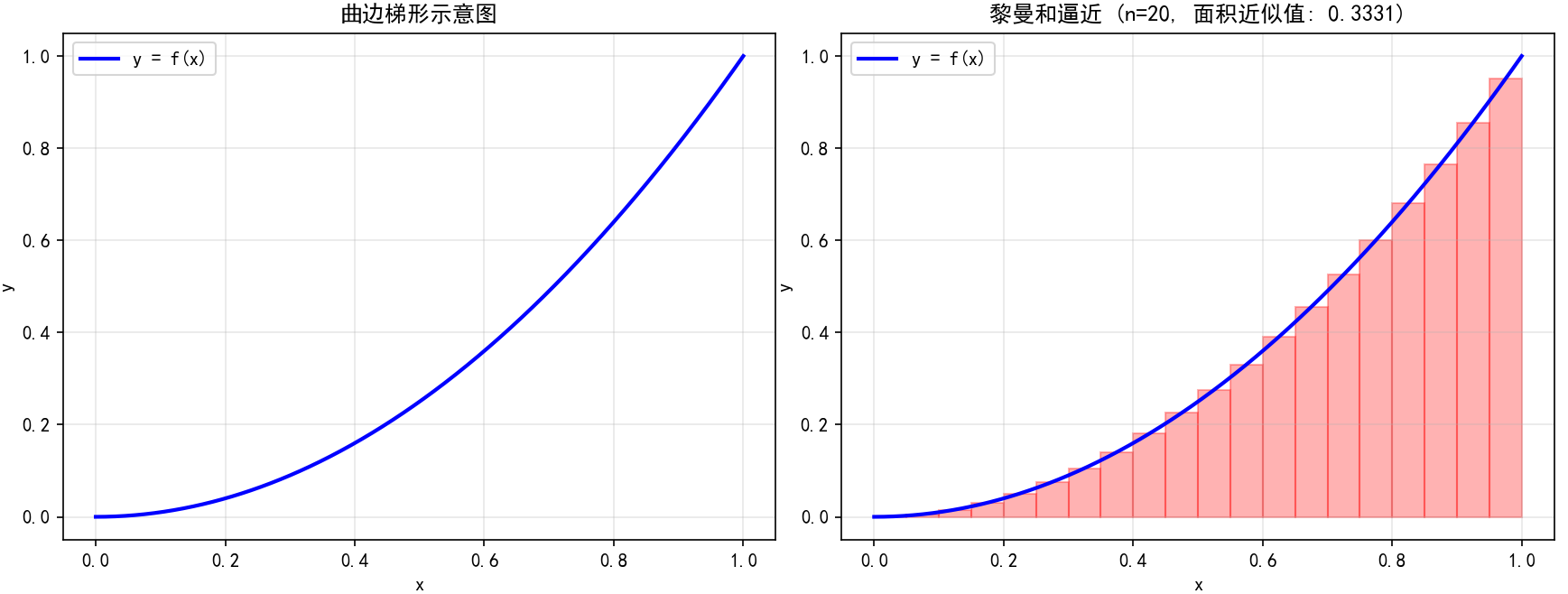

代码执行结果分析: 当运行上述代码时,你会看到随着矩形数量 n 的增加,红色矩形越来越紧密地填充在曲线下方,其总面积(黎曼和)也越来越接近曲边梯形的真实面积。
二、定积分的精确定义
2.1 黎曼和的构造过程
设函数 f(x)f(x)f(x) 在区间 [a,b][a, b][a,b] 上有定义,定积分的精确定义基于以下四个步骤:
步骤1:区间划分 将区间 [a,b][a, b][a,b] 任意划分为 nnn 个子区间: a=x0<x1<x2<⋯<xn−1<xn=ba = x_0 < x_1 < x_2 < \cdots < x_{n-1} < x_n = ba=x0<x1<x2<⋯<xn−1<xn=b
每个子区间 [xk−1,xk][x_{k-1}, x_k][xk−1,xk] 的长度为: Δxk=xk−xk−1(k=1,2,⋯,n)\Delta x_k = x_k - x_{k-1} \quad (k = 1, 2, \cdots, n)Δxk=xk−xk−1(k=1,2,⋯,n)
划分的精细程度用最大子区间长度表示: λ=max{Δx1,Δx2,⋯,Δxn}\lambda = \max\{\Delta x_1, \Delta x_2, \cdots, \Delta x_n\}λ=max{Δx1,Δx2,⋯,Δxn}
步骤2:取样点选择 在每个子区间 [xk−1,xk][x_{k-1}, x_k][xk−1,xk] 上任取一点 ξk\xi_kξk,即: ξk∈[xk−1,xk]\xi_k \in [x_{k-1}, x_k]ξk∈[xk−1,xk]
步骤3:黎曼和构造 构造和式: In=∑k=1nf(ξk)ΔxkI_n = \sum_{k=1}^n f(\xi_k) \Delta x_kIn=k=1∑nf(ξk)Δxk 这个和式称为函数 f(x)f(x)f(x) 在区间 [a,b][a, b][a,b] 上的黎曼和或积分和。
步骤4:极限定义 如果当划分越来越细(即 λ→0\lambda \to 0λ→0)时,黎曼和的极限存在且与划分方式及取样点选择无关,则这个极限值就是定积分: ∫abf(x)dx=limλ→0∑k=1nf(ξk)Δxk\int_a^b f(x) dx = \lim_{\lambda \to 0} \sum_{k=1}^n f(\xi_k) \Delta x_k∫abf(x)dx=λ→0limk=1∑nf(ξk)Δxk
2.2 定积分的各部分名称
- 被积函数:f(x)f(x)f(x)
- 积分变量:xxx
- 积分下限:aaa
- 积分上限:bbb
- 被积表达式:f(x)dxf(x)dxf(x)dx
- 积分号:∫\int∫
2.3 定积分的基本性质
-
积分值与积分变量无关: 定积分 ∫abf(x)dx\int_a^b f(x) dx∫abf(x)dx 的值是一个常数,∫abf(x)dx\int_a^b f(x) dx∫abf(x)dx 的大小只与被积函数 f(x) 及积分区间[a, b] 有关, 而与 积分变量 x 无关,所以:
∫abf(x)dx=∫abf(t)dt=∫abf(u)du\int_a^b f(x) dx = \int_a^b f(t) dt = \int_a^b f(u) du∫abf(x)dx=∫abf(t)dt=∫abf(u)du -
端点性质: ∫aaf(x)dx=0\int_a^a f(x) dx = 0∫aaf(x)dx=0 ∫abf(x)dx=−∫baf(x)dx\int_a^b f(x) dx = -\int_b^a f(x) dx∫abf(x)dx=−∫baf(x)dx
三、定积分的几何意义
3.1 非负函数的几何意义
当 f(x)≥0f(x) \geq 0f(x)≥0 在 [a,b][a, b][a,b] 上连续时,定积分 ∫abf(x)dx\int_a^b f(x) dx∫abf(x)dx 表示由曲线 y=f(x)y = f(x)y=f(x)、直线 x=ax = ax=a、x=bx = bx=b 和 xxx 轴所围成的曲边梯形的面积。
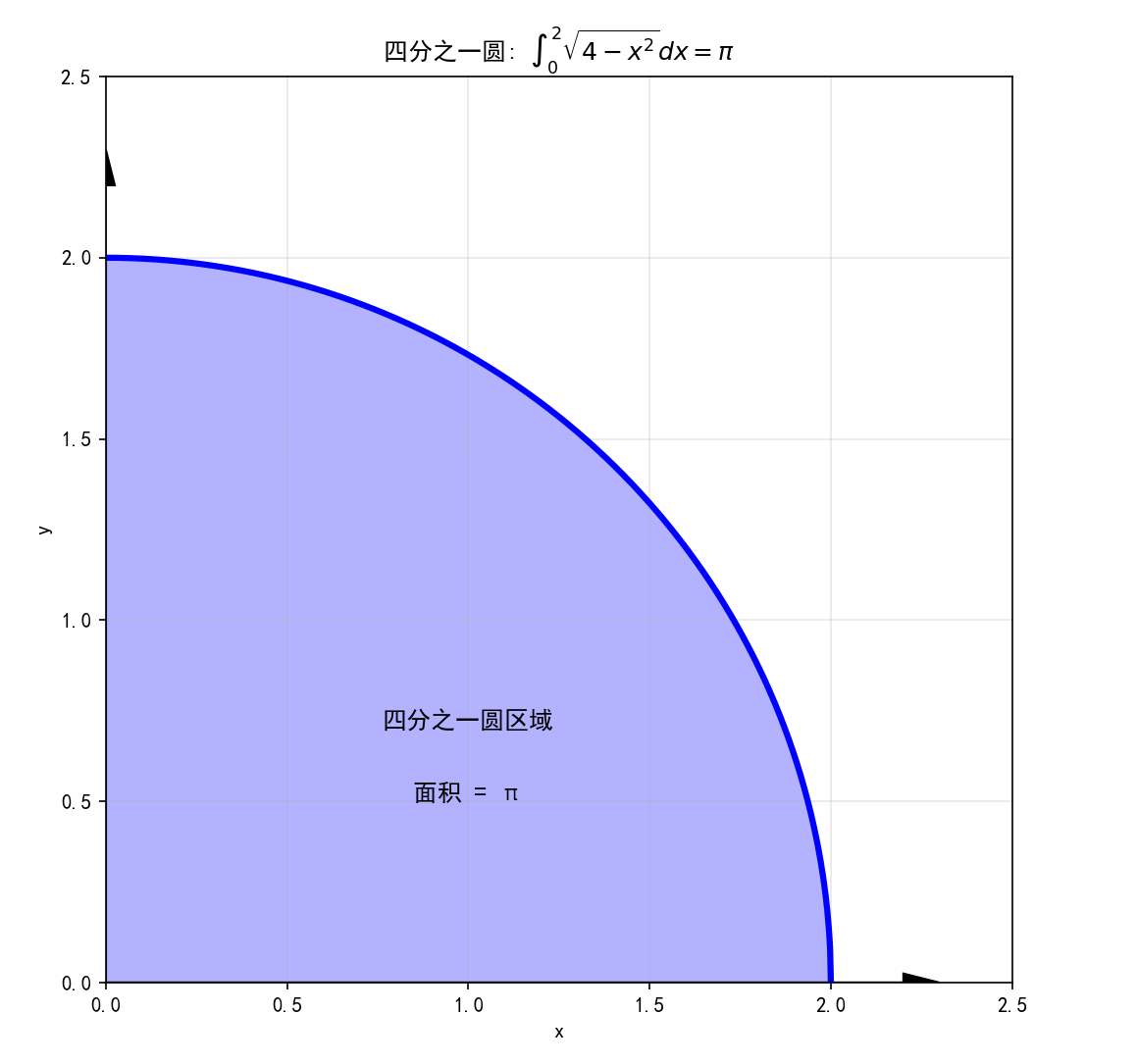
经典示例:计算 ∫024−x2dx\int_0^2 \sqrt{4-x^2} dx∫024−x2dx
这个积分表示的是四分之一圆的面积(半径为2)。
根据圆的面积公式 A=πr2=π⋅22=4πA = \pi r^2 = \pi \cdot 2^2 = 4\piA=πr2=π⋅22=4π,四分之一圆的面积为: ∫024−x2dx=14⋅4π=π\int_0^2 \sqrt{4-x^2} dx = \frac{1}{4} \cdot 4\pi = \pi∫024−x2dx=41⋅4π=π
让我们通过可视化来理解:
import numpy as np
import matplotlib.pyplot as plt
import mathdef visualize_circle_area():"""可视化四分之一圆面积的计算"""# 创建半圆曲线x = np.linspace(0, 2, 1000)y = np.sqrt(4 - x**2)fig, ax = plt.subplots(figsize=(10, 8))# 绘制四分之一圆ax.plot(x, y, 'b-', linewidth=3, label='y = √(4-x²)')ax.fill_between(x, y, alpha=0.3, color='blue')# 添加标注ax.text(1, 0.7, '四分之一圆区域', fontsize=12, ha='center')ax.text(1, 0.5, '面积 = π', fontsize=12, ha='center')# 设置坐标轴ax.set_xlim(0, 2.5)ax.set_ylim(0, 2.5)ax.set_xlabel('x')ax.set_ylabel('y')ax.set_title('四分之一圆: ∫₀² √(4-x²) dx = π')ax.grid(True, alpha=0.3)ax.set_aspect('equal')# 添加坐标轴箭头ax.arrow(0, 0, 2.2, 0, head_width=0.05, head_length=0.1, fc='k', ec='k')ax.arrow(0, 0, 0, 2.2, head_width=0.05, head_length=0.1, fc='k', ec='k')plt.show()# 计算数值结果theoretical_area = math.pinumerical_area, error = quad(lambda x: np.sqrt(4-x**2), 0, 2)print(f"理论值 (π): {theoretical_area:.10f}")print(f"数值计算: {numerical_area:.10f}")print(f"绝对误差: {abs(numerical_area - theoretical_area):.2e}")visualize_circle_area()
运行结果:
理论值 (π): 3.1415926536
数值计算: 3.1415926536
绝对误差: 8.88e-16
3.2 一般情况的几何意义
- 当 f(x)≤0f(x) \leq 0f(x)≤0 时:定积分值为曲边梯形面积的相反数
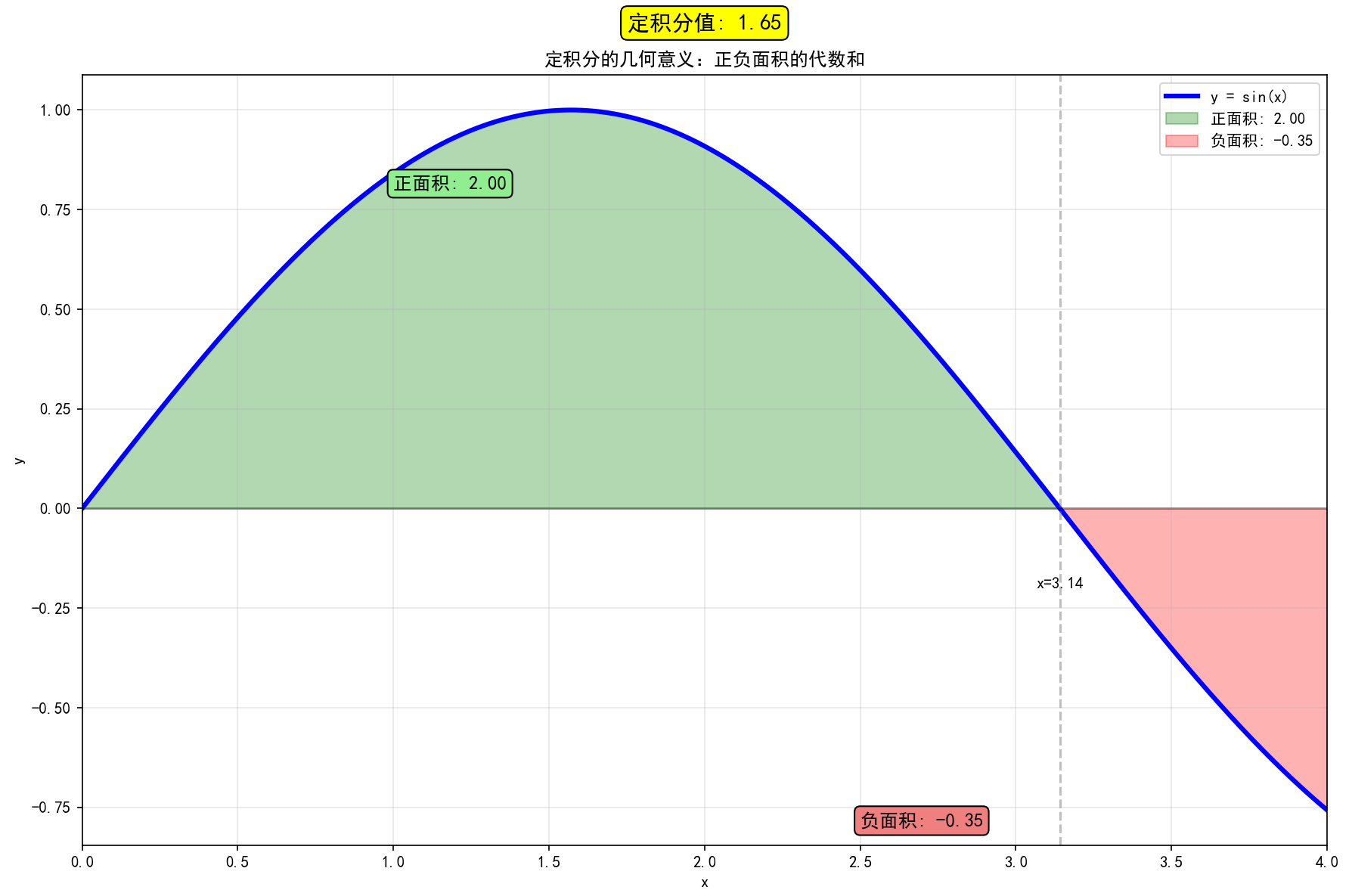
- 当 f(x)f(x)f(x) 变号时:定积分值为各部分面积的代数和(xxx轴上方取正,下方取负)
下面通过可视化展示这种情况:
def visualize_signed_area():"""可视化有正负面积的函数积分"""# 创建一个在x轴上下都有值的函数x = np.linspace(0, 4, 1000)y = np.sin(x) # 正弦函数在区间内会穿越x轴fig, ax = plt.subplots(figsize=(12, 8))# 绘制函数曲线ax.plot(x, y, 'b-', linewidth=3, label='y = sin(x)')ax.axhline(y=0, color='k', linestyle='-', alpha=0.3) # x轴# 填充不同区域(不同颜色)# x轴上方区域(正面积)ax.fill_between(x, y, where=y>0, alpha=0.3, color='green', label='正面积')# x轴下方区域(负面积)ax.fill_between(x, y, where=y<0, alpha=0.3, color='red', label='负面积')# 计算各部分面积area_positive = quad(lambda x: max(0, np.sin(x)), 0, 4)area_negative = quad(lambda x: min(0, np.sin(x)), 0, 4)total_area = area_positive + area_negative# 添加标注ax.text(1, 0.8, f'正面积: {area_positive:.2f}', fontsize=12)ax.text(2.5, -0.8, f'负面积: {area_negative:.2f}', fontsize=12)ax.text(2, 1.2, f'定积分值: {total_area:.2f}', fontsize=14, ha='center', bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow"))ax.set_xlabel('x')ax.set_ylabel('y')ax.set_title('定积分的几何意义:正负面积的代数和')ax.grid(True, alpha=0.3)ax.legend()plt.show()visualize_signed_area()
运行结果:
四、定积分概念的实际应用
定积分概念不仅仅是一个抽象的数学工具,它在实际问题中有直接的应用:
4.1 物理应用:变速直线运动的路程
对于做变速直线运动的物体,如果知道其速度函数 v(t)v(t)v(t),那么从时间 aaa 到 bbb 所经过的路程可以表示为: s=∫abv(t)dts = \int_a^b v(t) dts=∫abv(t)dt
4.2 经济应用:总成本计算
在经济学中,如果知道边际成本函数 MC(q)MC(q)MC(q),那么生产从 000 到 QQQ 单位产品的总成本为: TC=∫0QMC(q)dqTC = \int_0^Q MC(q) dqTC=∫0QMC(q)dq
总结
定积分的核心概念可以概括为以下几点:
- 思想基础:采用"分割-近似-求和-取极限"的方法解决曲边梯形面积问题
- 精确定义:基于黎曼和的极限概念,与分割方式和取样点选择无关
- 几何意义:
- 当 f(x)≥0f(x) \geq 0f(x)≥0 时,表示曲边梯形的面积
- 一般情况下,表示函数图像与xxx轴所围面积的代数和
- 基本特征:定积分值是一个确定的常数,只与被积函数和积分区间有关
理解定积分的概念和几何意义是学习微积分后续内容的基础,特别是为理解牛顿-莱布尼茨公式奠定直观基础。
往期精彩回顾:
- 用Python来学微积分29-原函数与不定积分完全指南
- 用Python来学微积分30-微分方程初步
专栏导航目录 《程序员AI之路:从Python起步》完全学习导航
完整代码已开源 ai-learning-path,欢迎Star和Fork!
参考资料:
- 扈志明《微积分》教材
互动邀请:如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题,欢迎在评论区分享交流!
