浙江建设职业技术学院尔雅网站易捷网站内容管理系统漏洞

引言

前序学习进程中，已经对最佳超平面的求解有了一定认识。
刚好在此梳理一下:

函数距离

首先有函数距离F，也可以称为函数间隔F：
$$F=\underset{i=1...m}{\min }{y}_i(w\cdot x_i+b)$$

几何距离

然后有几何距离δ，也可以称为几何间隔δ：
$$\delta =\underset{i=1...m}{\min }{y}_i(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert })$$
很显然，几何距离δ和函数距离F之间只相差一个量||w||：
$$\delta =\frac{F}{\Vert w\Vert }$$然后我们再次回忆最佳超平面的寻找过程：

第一步，一个特定超平面的周围会有很多点，通过计算后会获得不同的几何距离，取出这些距离中的最小值；
第二步，遍历所有可能的超平面，重复步骤一；
第三步：在前两步的基础上，在取出的所有几何距离中，选取最大值对应的超平面为最优超平面。
这是一个稍微有点绕的过程，首先是每个备选超平面都选取最小几何距离，然后是在所有最小几何距离中挑出最大值，取这个最大的几何距离对应的超平面为最佳超平面。可以总结为：在最小值集合中挑选最大值。
为了寻找这个最大值，我们联想到同比率变换权重矩阵w和偏置量b不会改变几何距离，因此有一种巧妙的解法：
通过同比率调整权重矩阵w和偏置量b，使得函数距离F=1，这个时候最佳超平面对应的最大几何距离δmax满足:
$${\delta }_{max}=\underset{i=1...m}{\max }\frac{1}{\Vert w\Vert }$$
为求解这个最佳超平面对应的最大几何距离，一种更好理解的思路被提出来，把寻找过程中的除法转化为了乘法，定义距离函数f：
$$f=mi{n}_{i=1...m}\frac{1}{2}{\Vert w\Vert }^2$$这篇文章的学习任务，就是梳理距离函数f的最佳解法：拉格朗日乘数法。

拉格朗日乘数法

拉格朗日乘数法的构造需要两个前提条件，一个是目标函数，比如此处的距离函数f，另一个是约束函数，可以定义为g。
关于f和g，展开如下讨论：
f和g在任意位置的梯度都指向它们增长最快的方向，和它们本身的图像垂直；
对于目标函数f，它取特定值的时候，结果可能绘制出一条闭合的等高线，也可能是孤立的点。对于孤立的点，法向量是（0,0）；对于等高线，可以记录任意一点的梯度为$▽f$；
目标函数f和约束函数g可能有很多交点，但当目标函数取极值的时候，一定会满足条件：$$▽f=\lambda ▽g$$
为解释这个梯度平行的条件，我们这样想：
将f的梯度$▽f$分解到互相垂直的$▽g$和g的切线方向$v$上，此时沿着$v$的方向只要还有f的梯度，就表明f的取值还可以继续改变；
当$▽f$在$v$上没有任何分量时，f只能在垂直g的方向上增长，也就是沿着约束函数g再也无法改变f。
当然，f的取值也无法脱离g的约束，所以$▽f$在$v$上没有任何分量时，f就取到了极值，此时f的法向量垂直于g，g的法向量自然也垂直于g，这两个法向量平行，所以一定有：
$$▽f=\lambda ▽g$$

当f为孤立点时，λ=0，上式依然满足。
为辅助理解，求助了deepseek，它提供了一张图，放在这里和大家共享，也可复制链接直达原图：https://upload.wikimedia.org/wikipedia/commons/thumb/f/fa/Lagrange_multiplier.png/300px-Lagrange_multiplier.png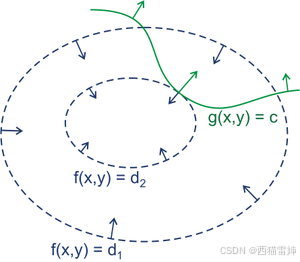

总结

学习了一下拉格朗日乘数法的基本概念。