算法题（254）：灾后重建

审题：
本题需要我们在有时间作为限定条件的情况下，找到特定时间时任意两点之间的最短路径

思路：

方法一：floyd算法

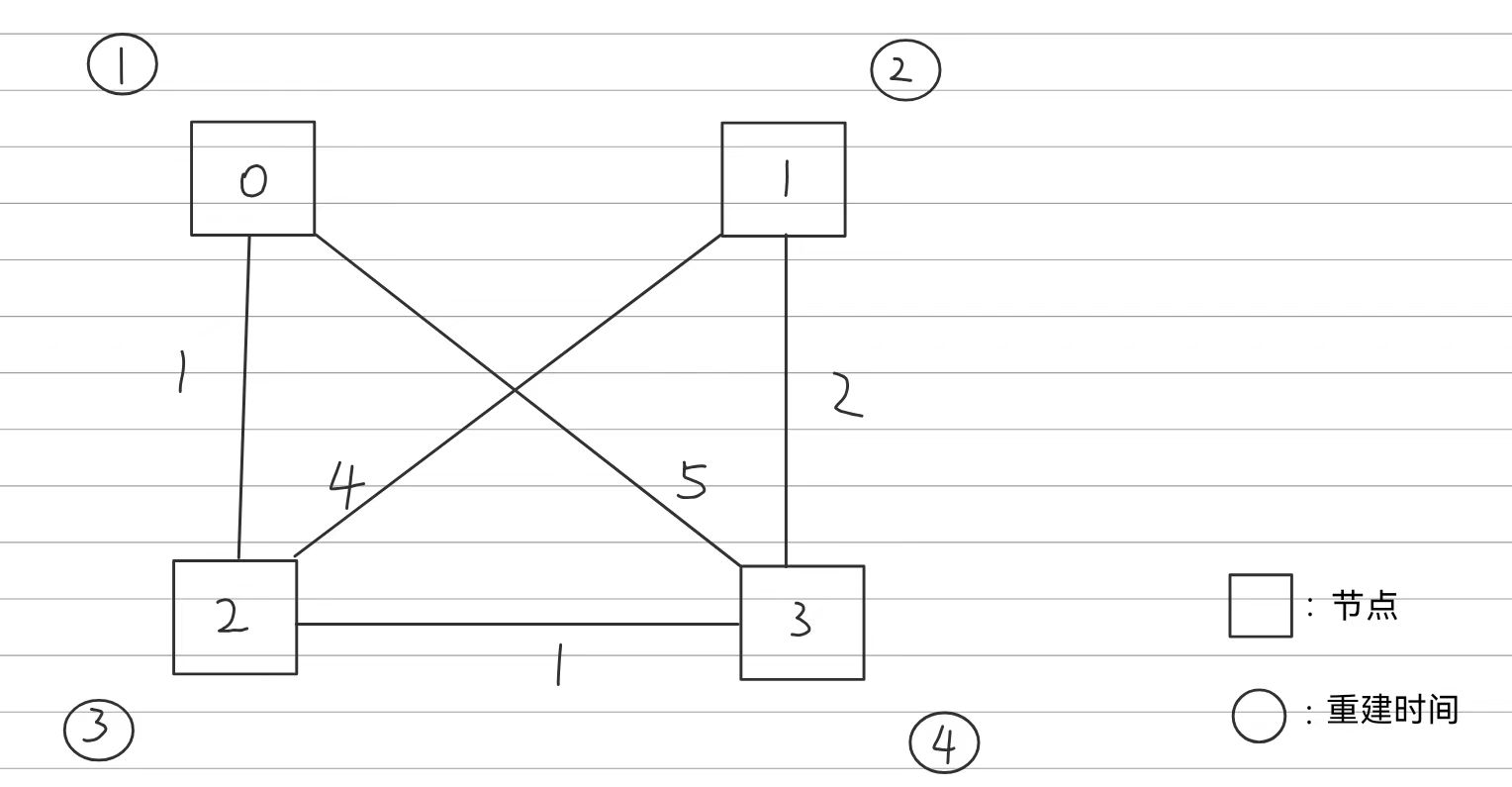
题目中会给定n个村庄（节点）的重建完成时间以及各个村庄之间的路径权值，然后进行k次询问，查询某个时间点的两个村庄的最短路径

注意：只有重建完成的村庄相关路径可走，在重建时间当天就可通路，节点重建时间递增，查询时间节点递增

输入样例解析：

第一轮询问：day2，求节点2与节点0之间的最短路径

此时只有0节点和1节点重建完成，将节点0和1纳入floyd算法的考虑，所以不存在最短路径，返回-1

第二轮询问：day2，求节点0与节点1之间的最短路径

由于0和1之间没有路径，所以不存在最短路径，返回-1

第三轮询问：day3，求节点0与节点1之间的最短路径

节点2加入floyd算法考虑，此时存在一条路径（0->2->1），长度为5

第四轮询问：day4，求节点0与节点1之间的最短路径

节点3加入floyd算法考虑，此时存在更短的路径(0->2->3->1),长度为4

综上，由于查询的t是逐渐递增，而我们的floyd算法的核心就是逐渐增加要考虑的点，所以我们的查询过程和floyd算法的计算过程是同步的，  只要根据给定查询天数进行指定次的floyd算法即可（相当于把第一层for循环给分解成n次调用floyd函数）

解题：
 

#include<iostream>
#include<cstring>
using namespace std;
const int N = 210, INF = 0x3f3f3f3f;
int n, m;
int t[N];
int f[N][N];//索引从0开始
void floyd(int k)
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){f[i][j] = min(f[i][j], (f[i][k] + f[k][j]));}}
}
int main()
{//数据录入cin >> n >> m;for (int i = 0; i < n; i++) cin >> t[i];//初始化fmemset(f, 0x3f, sizeof f);for (int i = 0; i < n; i++){f[i][i] = 0;}for (int i = 1; i <= m; i++){int l, r, v; cin >> l >> r >> v;f[l][r] = f[r][l] = v;}int cnt = 0, pos = 0;cin >> cnt;while (cnt--){int l, r, v; cin >> l >> r >> v;//进行分批的floydwhile (pos < n && t[pos] <= v){floyd(pos++);}//答案输出if (t[l] > v || t[r] > v || f[l][r] == INF) cout << -1 << endl;else cout << f[l][r] << endl;}return 0;
}

关键1：节点的下标是从0开始的

注意记录节点信息的时候从0开始

关键2：没有重边

没有重边，我们就可以直接传递边权值，而不用min

关键3：答案输出

若当前时间段，两个端点村庄存在没有重建完成的，直接输出-1，若路径不存在也是同理

否则就可以输出结果

P1119 灾后重建 - 洛谷