Prim 算法
PrimPrimPrim 算法
文章目录
- PrimPrimPrim 算法
- 一、前言
- 二、PrimPrimPrim算法
- 2.1 基本思想
- 2.2 步骤
- 2.3 实现
- 2.3.1 定义结构
- 2.3.2 PrimPrimPrim 算法
- 2.4 KruskalKruskalKruskal算法和PrimPrimPrim算法优缺点辨析
- 2.5 KruskalKruskalKruskal算法和PrimPrimPrim算法应用
- 三、小结
一、前言
先前已讲过了KruskalKruskalKruskal算法,是通过找(权值)最小的边来求得最小生成树的。今天的算法——Prim算法,将另辟蹊径,通过找顶点的方式最终确定最小生成树,接下来让我们一起揭开它神秘的面纱~
二、PrimPrimPrim算法
2.1 基本思想
贪心
学过HuffmanHuffmanHuffman树和KruskalKruskalKruskal算法之后,你是不是对贪心算法的基本含义已经很了解了,在这里它是怎样应用的呢?
每激活一个顶点,就选择当前节点到可到达顶点的最小权值的边,从而激活另一个顶点。
2.2 步骤
PrimPrimPrim算法的核心是激活顶点,因此,需要一个动态维护一个所有待激活的顶点的数组——mark数组。
最小生成树既然是找最小权值,自然离不开权值数组,方便做出最优选择——cost数组。
在形成最小生成树的过程中,我还想记录最小生成树的所有路径,因此需要一个visited数组,记录待激活顶点的前置顶点(上一个激活的顶点),从而确定完整的边。
-
从图中,任意选取一个顶点,激活它,发现新的边。
-
找到权值数组(以该点出发的边的权值数组)里最小的边,激活另外一个顶点。
如果说从一个顶点出发,到某一个顶点的距离一样怎么选择呢?
小孩子才做选择,成年人全都要~所以这两个方向形成的生成树都成立。
但是最小生成树的中最小是向来不能忽略的,一定是权值之和最小的存在,尽管在形成过程中,可能走向不同的方向,但是最终只有权值最小的存在才是最小生成树。
所以说,最小生成树可能不唯一,但是最小生成树的权值之和一定是唯一的。
如图:

最终形成的两种生成树都是最小生成树(蓝线画的)
-
更新权值数组,继续找最小的边,激活另外的顶点。(重复)
-
直到所有顶点都激活。
2.3 实现
2.3.1 定义结构
还是借助邻接矩阵来实现,利用边集数组来存储边~
/* 边集的结构 */
typedef struct
{int begin; // 边的起点(顶点1)int end; // 边的终点(顶点2)int weight; // 边的权值
} EdgeSet;initMGraph(graph, names, sizeof(names)/sizeof(names[0]), 0, INF);
为什么在所有顶点未激活时,将所有权值设置为
INF?
标识未访问的状态。
确保起点能被优先选择:算法需要从一个起点开始构建最小生成树,将起点设置为0,而其他是
INF,确保起点能顺利激活。为权值提供安全基准:每当考虑一个新顶点加入最小生成树中时,都需要检查并更新它的所有邻居顶点与当前最小生成树的距离。初始的INF作为一个巨大的值,确保了在第一次比较时,任何一条实际存在的、权重小于INF的边都能顺利触发更新操作。
2.3.2 PrimPrimPrim 算法
// parameter:
// graph: 指向邻接矩阵的图结构
// startV: 表示激活的第一个顶点坐标
// result: 表示最小生成树的边的激活情况
int PrimMGraph(const MGraph *graph, int startV, EdgeSet *result)
{// cost数组表示图中各顶点的权值数组。不断更新已激活顶点能接触到的顶点之间边的权值int *cost = malloc(sizeof(int) * graph->nodeNum);// mark表示图中顶点激活的状态:0-未激活;1-已激活int *mark = malloc(sizeof(int) * graph->nodeNum);// 从哪个顶点开始访问,-1表示没有被访问到,访问到被赋予激活顶点的索引int *visited = malloc(sizeof(int) * graph->nodeNum);// 保存权值int sum = 0;// 更新第一个节点激活的状态for(int i = 0; i < graph->nodeNum; i++){// 初始化cost[i] = graph->edges[startV][i];// 表示一开始都未被激活mark[i] = 0;// 更新visited信息,从哪个节点可以访问if(cost[i] < INF){visited[i] = startV;}else{visited[i] = -1;}}// 激活mark[startV] = 1;int k = 0;// 动态激活节点,找最小值for (int i = 0; i < graph->nodeNum - 1; ++i) // 遍历边(最小生成树n - 1条){int min = INF;k = 0;for (int j = 0; j < graph->nodeNum; ++j){if (mark[j] == 0 && cost[j] < min){min = cost[j];k = j;}}mark[k] = 1;result[i].begin = visited[k];result[i].end = k;result[i].weight = min;sum += min;// 每激活一个顶点,需要更新cost数组和visited数组for (int j = 0; j < graph->nodeNum; ++j){if (mark[j] == 0 && graph->edges[k][j] < cost[j]){cost[j] = graph->edges[k][j];visited[j] = k;}}}// 释放free(cost);free(mark);free(visited);// 放回最小权值return sum;
}
如图:
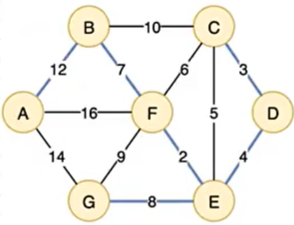

有没有发现用PrimPrimPrim 算法找到的最小生成树和先前KruskalKruskalKruskal 算法找到的是一样的。其实有的图用这两种方法找到的是不一样的。但请记住:(还是那句话)最小生成树可能不唯一,但是最小生成树的权值之和一定是唯一的。
学习了两种算法的精髓之后,你是不是对它们有了更加深刻的认识,让我们一起来梳理一下吧~
2.4 KruskalKruskalKruskal算法和PrimPrimPrim算法优缺点辨析
KruskalKruskalKruskal算法:代码简洁易于理解,逻辑直接,时间复杂度取决于边的排序。
PrimPrimPrim算法:运行效率高,且图很稠密,时间复杂度取决于存储结构。
2.5 KruskalKruskalKruskal算法和PrimPrimPrim算法应用
- 适用场景:
KruskalKruskalKruskal算法更适合于稀疏图:因为它对于边是有一定要求的,它是以边为出发点,从而将各个顶点连接起来。
PrimPrimPrim算法更适合稠密图:因为它主要是以激活顶点为目的,无关边的数量。
三、小结
经过本篇,相信你已经明白如何确定一个图的最小生成树。
下一篇,我们将开启新的图的一种应用——最短路径。这和最小生成树很相似,但根本目的是不同的。期待inginging
希望各位多多指教~
