斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记 | Lecture 7: Parallelism 1

前言

学习斯坦福的 CS336 课程，本篇文章记录课程第七讲：并行化（上），记录下个人学习笔记，仅供自己参考😄

website：https://stanford-cs336.github.io/spring2025

video：https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_

materials：https://github.com/stanford-cs336/spring2025-lectures

course material：https://github.com/stanford-cs336/spring2025-lectures/tree/main/nonexecutable/7-Parallelism basics.pdf

1. Outline and goals

从本次课程开始我们将进入多机优化环节，本次讲座的重点将围绕 跨机器并行 展开，目标是从优化单个 GPU 的吞吐量转向理解训练超大规模模型所需的复杂机制与技术细节

当模型规模扩大时，单个 GPU 已无法容纳整个模型，因此必须将模型拆分到不同机器上，同时还需要充分利用所有可用服务器资源来实现快速训练，我们需要同时解决 计算能力和内存容量 这两大核心问题。不同机器间的通信环境将呈现显著的异构性特征，GPU 之间存在着多种层级的差异化通信模式，这将催生多样化的并行化范式

开发者们往往同时采用多种并行化策略的组合方案，接下来我们将逐一解析当前最主流的几种并行化方案，随后我们将探讨如何将这些方案有机结合，从而实现超大规模模型的高效训练。最后，我们将通过实际案例展示业界如何运用这些并行化策略来开展大规模分布式训练

本次讲座的各个章节安排如下：

• Part 1: Basics of networking for LLMs
• Part 2: Different forms of parallel LLM training
• Part 3: Scaling and training big LMs with parallelism

首先我们将讲解网络基础架构，接着探讨这些网络硬件概念如何对应不同的并行化策略，最后通过实际案例展示整体协同工作

2. Part 1: Basics of networking for LLMs

2.1 Limits to GPU-based scaling – compute and memory

上次讲座我们向大家介绍过 GPU 的算力增长趋势，每块 GPU 的浮点运算能力呈现出惊人的超指数级增长曲线，这个攀升幅度确实令人震撼

但若想同时快速扩展计算能力和内存容量仅靠单块 GPU 显然力有不逮，我们还需要等待数年时间才能见证这条曲线持续向上攀升。因此，若想当下就训练出真正强大的语言模型，我们必须依赖多机并行技术

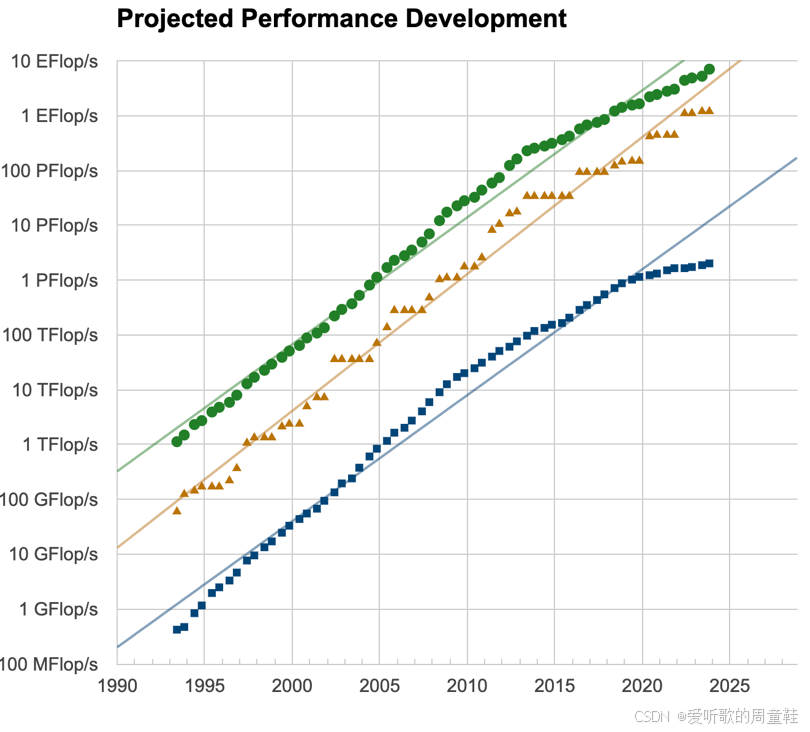
观察全球最快的超级计算机，如上图所示，这些顶尖系统的计算能力已达到每秒百亿亿次浮点运算级别，这些正是上图的绿色线条所代表的性能指标，若想训练当今最庞大、最强大的语言模型，这些超级计算机正是我们必须仰仗的核心利器，这正是在计算层面需要考虑多机并行的根本原因

除了算力考量，内存因素同样迫使我们采用多机并行方案，因此，算力与内存这两大核心资源正是我们必须重点考量的关键所在。

就内存需求而言，当前许多模型的体量已变得相当庞大，当然 GPU 的内存容量也在提升，但增长速度远不及模型需求的扩张，单个 GPU 已无法容纳这些大型模型。或许在遥远的未来，我们将不再需要为这些问题困扰，但当模型参数规模突破数十亿量级时，单个 GPU 显然已无法承载，因此我们必须严格遵守现有内存限制

这就是我们必须面对的现实挑战，我们需要哪些工具才能应对这些挑战呢？

GPU 从来都不是以单卡形式存在的，每台物理机架内的单台机器都会配备多块 GPU，这里有个典型示例，这个示例引自 GPT-NeoX-20B 论文，虽然这是个旧案例，但同样适用于我们课堂上使用的 H100 设备

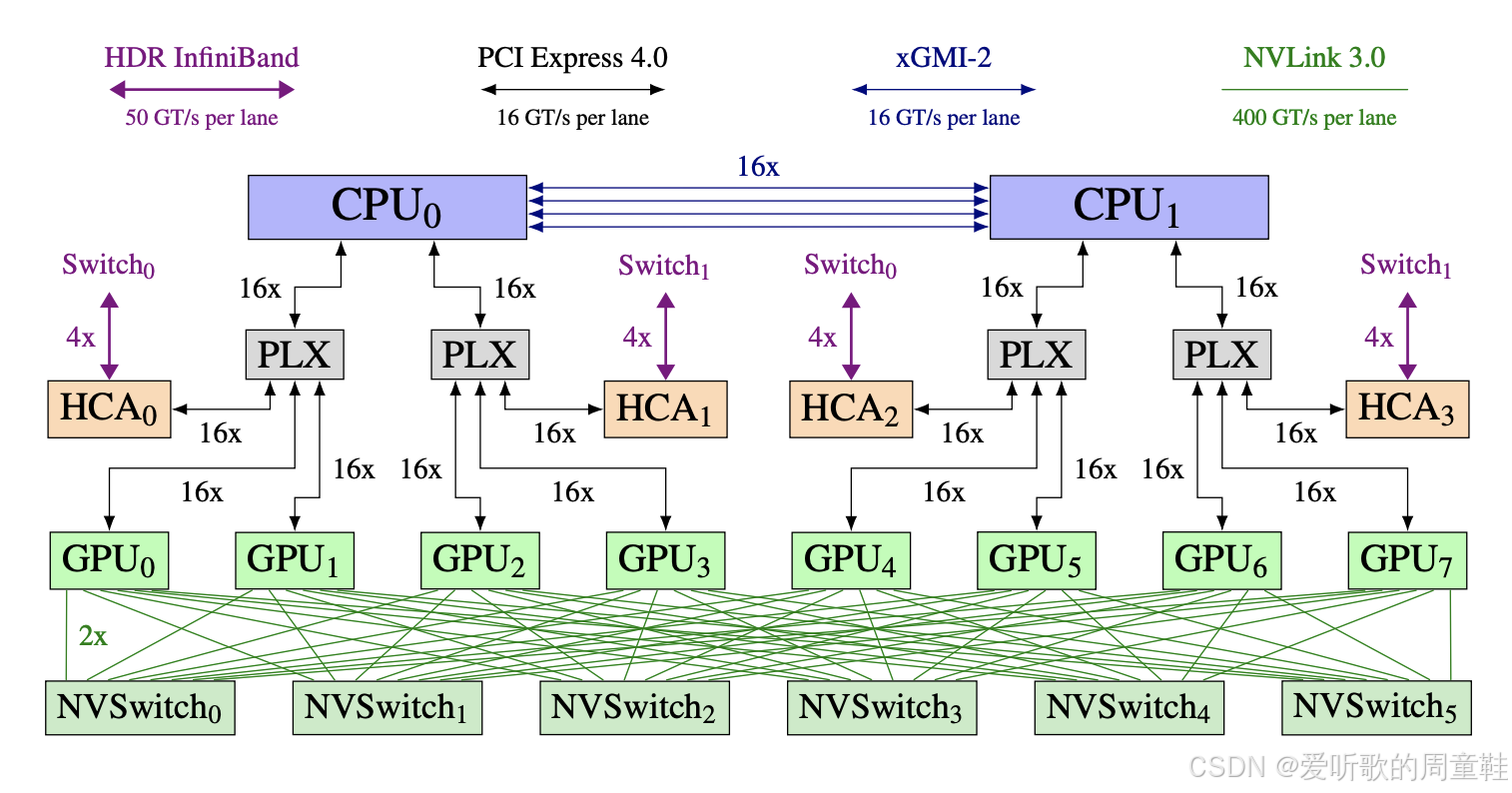
如上图所示，这里部署了 8 块 GPU，这些 GPU 通过高速互联网络与多颗 CPU 相连，每块 GPU 底部都配置了 NVSwitch 高速交换模块，这 8 块 GPU 之间通过极高速的互联通道相连。但当这 8 块 GPU 需要与其他机器上的 GPU 通信时，则必须经由网络交换机进行中转

图中紫色标识线显示采用的是 HDR InfiniBand 高速网络，相比 NVLink 内部内联，这种外部连接的传输效率明显较低，单通道传输带宽差距明显，外部连接速率约为内部互联的八分之一。这种硬件层级结构将深刻影响我们实际部署模型并行化的具体方案，在后续讲解过程中，请始终将这个硬件架构模型牢记于心

单台机器内部的连接通道具有极高的传输速率，而跨机器通信时，传输效率则会显著下降，若继续扩展规模（例如连接超过 256 块 GPU 时），根据所用硬件类型，通信效率还可能面临更深层次的衰减

2.2 Some basics about collective communication

下面我们来简要回顾下几种集体通信操作，之所以要特别强调这一点，是因为存在一个关键等式关系，只有掌握它才能深入理解并行算法性能特征中的精妙之处，接下来我们将逐一解析这些操作，并重点阐述一个关键性能影响因素

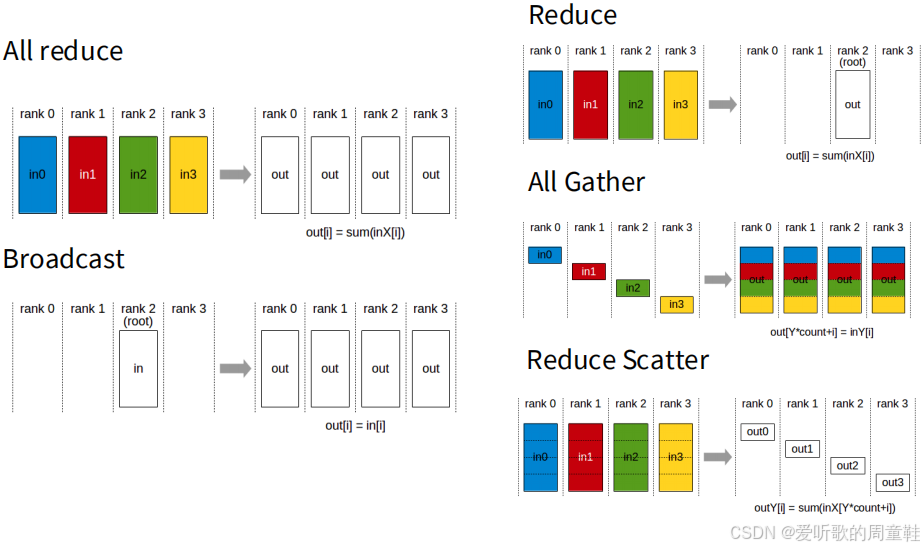
首先介绍的是 全归约操作（all reduce），相信大家都不陌生，假设有四台机器（即四个计算节点），每台都存储着各自的数据分片，此时需要执行某种归约运算（reduction operation），以求和运算为例：我们需要将所有输入数据相加，并将最终结果同步复制到每台机器上，这个操作的计算成本大约是待归约数据总量的两倍，其中包含一次广播操作

在这个场景中，我们将从二号计算节点（rank 2）获取单一输入数据，并将其复制分发到所有其他计算节点，该操作的通信成本大致与输出数据总量成正比，约为数据总量的 1 倍。接下来是归约操作：将来自不同计算节点的输入数据汇总求和，最终结果仅发送至单一目标机器

还有两种虽不常见但至关重要的操作：全聚集（all gather）和归约分散（reduce scatter），全聚集（all gather） 操作是指：从零号计算节点（rank 0）提取参数的一个子组件，并将其复制到所有其他计算节点，同理，对一号（rank 1）、二号（rank 2）、三号（rank 3）等所有计算节点都执行相同操作，每个计算节点各自处理参数的不同分区，随后将这些分区数据同步复制到集群中的所有其他机器，这就是将本地数据广播至所有节点的过程

而 归约分散（reduce scatter） 则是：对数据行执行求和操作后，仅将结果发送至零号计算节点（rank 0），这相当于全归约（all reduce）操作的部分实现，通过上面的示意图，可以清晰理解归约分散（reduce scatter）的工作原理

全聚集（all gather）和归约分散（reduce scatter）之所以至关重要是因为它们本质上构成了众多并行算法的底层基础构件，因此这一等价关系具有重要价值，这个关键要点我们将在课程中反复强调

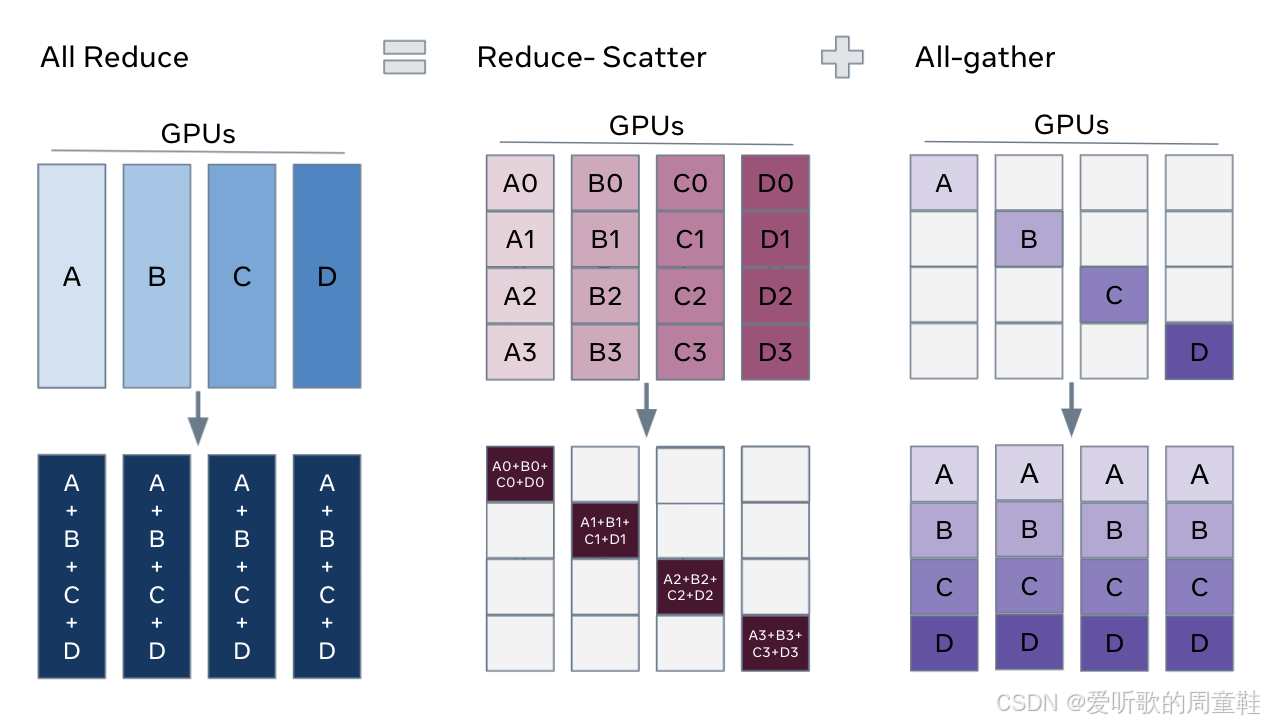
假设我们需要执行全归约（all reduce）操作：现有四块 GPU（A、B、C、D），每块 GPU 分别处理不同的数据点，此时每块 GPU 针对各自数据点计算出不同的梯度值，需要先对这些梯度进行求和运算，再将汇总后的梯度结果同步回所有 GPU 设备，这正是典型的跨四块 GPU 实现的数据并行操作，因此该场景正适合使用全归约操作

但需注意：该操作可拆解为两个步骤，先执行归约分散（reduce scatter）对各行梯度分别求和，将结果分散存储在 GPU 0/1/2/3 中，再通过全聚集（all gather）同步数据，随后通过全聚集操作将这些汇总结果广播复制到其余 GPU 上，此时每块 GPU 都获得部分参数的总和结果，随后会将这些数据同步复制到其他工作节点，在带宽受限的情况下，这基本上就是最优的解决方案了

全归约在最优情况下，其性能表现大致等同于归约分散（reduce scatter）加全聚集（all gather）所能达到的带宽极限。全归约（all reduce）与上图右侧方案（归约分散 + 全聚集）的通信操作次数就能直观验证这一点

2.3 TPUs vs GPUs – design differences at the comm level

在开始讲解并行化算法之前，最后要简单提一下 GPU 与 TPU 的对比，这也是本次讲解中唯一会涉及二者区别的部分，这次讨论的内容大多可以忽略底层硬件差异，但有一点至关重要，我们需要提前说明，以便后续讨论引用

GPU 中如何实现多台机器或多个加速器之间的网络互联的呢？

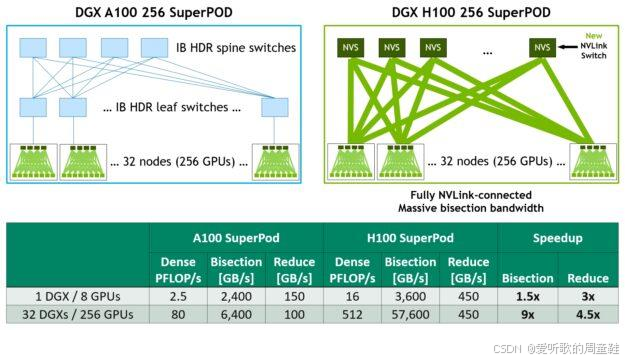
正如前面在 GPT NeoX 中所展示的，GPU 集群的典型架构是这样的：每个计算节点（即单台物理机器）通常配备 8 块 GPU，这些节点之间通过高速交换机实现互联，这些机器通过全互联拓扑组网，最多可扩展至 256 块 GPU 的规模。

GPU 的规模是个关键阈值，在此范围内（256），机器之间都能保持高速的任意通信，此时网络传输速率将显著下降，而当规模突破单机柜的 GPU 容量限制后，就需要通过叶脊交换机架构进行通信

反观谷歌的 TPU 设计，其机器组网方案采用了截然不同的技术路线，每块 TPU 芯片都能与相邻芯片实现超高速互联，这种被称为 “环形网格” 的拓扑结构具有极佳的可扩展性，但每块芯片仅能与相邻节点直接通信

之所以在全归约相关内容后立即讨论这个架构，是因为像全归约、归约分散这类集合通信操作，在环形网格上的实现效率完全可以媲美全互联架构，因此若纯粹针对集合通信进行优化，采用 TPU 网络架构比 GPU 网络更具优势，后续讲解各类并行化操作时，我们会具体分析这种架构的优劣特性

2.4 Part 1 recap

现在让我们整理思路，开始探讨一个新的计算单元概念，新的计算单元不再是单个 GPU，而是整个数据中心，整个数据中心将成为我们实施计算的基本单元

现在我们需要设计算法和分片策略，以实现两个关键目标：首要目标是实现内存的线性扩展，随着 GPU 数量的增加，可训练的最大模型规模将实现线性增长，这意味着只要资源充足，我们就能训练越来越庞大的模型。另一个关键目标是实现计算能力的线性扩展，随着 GPU 数量的增加，用于模型训练的有效计算能力也将呈线性提升

最终，这些目标构成了我们工作的核心，这些算法只需通过不同方式调用这些极其简单的集体通信原语即可实现，因此，在评估这些并行算法的性能特征时，本质上只需分析集体通信原语的调用次数即可，这种思考方式至关重要，我们在此并不深入探讨这些算法的底层实现细节

3. Part 2: Different forms of parallel LLM training

我们需要重点关注的并行化策略主要分为三类：

• Data parallelism
  • Naïve data parallel
  • ZeRO levels 1-3
• Model parallelism
  • Pipeline parallel
  • Tensor parallel
• Activation parallelism
  • Sequence parallel

首先是数据并行，数据并行的核心思想是：在不同 GPU 之间大致复制相同的参数副本，无需对参数进行拆分，而是将训练批次数据分割处理，不同 GPU 或计算节点将分别处理批次数据的不同分片。这就是数据并行的基本原理，具体实现过程中存在诸多精妙之处

模型并行则采用不同思路：不再让所有 GPU 都存储完整模型，而是将模型的不同部分分配到不同计算单元，随着模型规模不断扩大，这种全复制方式将带来严重的存储压力，因此必须采用智能的模型切分策略，让不同 GPU 分别处理模型的特定组成部分，这种分布式计算方式就是模型并行

最后的关键环节是激活值并行，由于 PyTorch 框架对激活值的透明化处理，我们在日常开发中往往无需过多关注这一环节。但随着模型规模持续扩大，序列长度不断增长，激活值占用的显存将演变成严峻的技术瓶颈，因此，当需要以超大批次规模训练这些巨型模型时，必须采用特殊技术手段来管控激活值的内存占用，因此我们同样需要对激活值进行切分处理，目前已有多种技术方案可应对这一挑战

当我们将这些技术方案有机整合后，便掌握了实现算力与内存优雅扩展的全套工具链，足以支撑海量计算节点的高效协同，这些构成了最核心的概念体系，接下来我们将深入探讨如何高效实现这些核心概念

3.1 Data parallelism

3.1.1 Naive data parallelism

数据并行的基础实现始于随机梯度下降算法，当我们采用最基础的批量随机梯度下降时，其计算公式如下所示：

$${\theta }_{t+1}={\theta }_t-\eta \sum _{i=1}^B\nabla f(x_i)$$

我们选取批量为 $B$ 的样本，汇总所有梯度后对参数进行更新。最基础的数据并行实现，就是将批量 $B$ 切分后分配到不同计算节点上执行，每个计算节点将独立完成部分梯度求和运算，随后通过梯度同步交换实现全局参数更新，在每次梯度更新前，先完成梯度同步再进行参数更新

前面我们讨论了计算能力与内存扩展等关键要素，那么我们就来逐一剖析这些方案的具体实现

在计算扩展方面，数据并行确实表现出色，每台机器 / 每个 GPU 将分配到 B/M 个样本，当总批次规模足够大时，每个 GPU 都能获得相当可观的子批次规模，这样就有望充分发挥其计算潜力，这个方案确实不错

那通信开销如何呢？每处理一个批次，都需要传输两倍于模型参数量的数据，注意，全归约操作的通信开销大约是待归约数据量的两倍，因此，只要批次规模足够大，这个方案就完全可行，当采用足够大的批次规模时，梯度同步产生的通信开销就能被计算量有效掩盖

内存扩展性这个问题，我们现在完全没涉及，每块 GPU 都需要完整复制整套参数，它必须完整复制优化器的状态数据，这对内存扩展性相当不利，若不考虑内存限制，这个策略其实完全可行

但实际应用中，内存始终是个绕不开的瓶颈，大家可能都经历过这样的场景：当你试图将大模型塞进 GPU 时，PyTorch 总会弹出那个熟悉的提示—内存不足，这确实会严重影响训练效果，毕竟若能容纳更大的批次尺寸，数据并行的效率将获得显著提升，因此最理想的情况是能实现内存的高效利用。

现在让我们来深入剖析基础数据并行的内存消耗问题，实际情况是内存消耗比表面看起来更为严峻，这种情况其实相当糟糕，虽然大家在第一次作业中已经实践过，但我们不妨仔细思考：究竟需要存储多少份模型副本呢？

这个数字会非常惊人，实际上，我们需要存储大约五份权重副本，根据训练采用的精度不同，每个参数大约需要存储 16 字节的数据量。这种情况确实相当棘手，因为单从模型参数来看，理论上每个参数只需要 2 字节存储空间，那么 8 倍的存储开销从何而来呢？

首先，梯度数据是必须存储的，若采用 BF16 格式计算梯度，每个参数又额外占用 2 字节，随后优化器状态的出现带来了大问题，你需要 4 字节存储主权重（即 SGD 中用于累加的中间求和结果），Adam 优化器还需要 4 或 2 字节存储一阶矩估计（用于记录历史梯度），同时 Adam 还需二阶矩估计（记录历史梯度的方差），这又需要占用 4 或 2 字节的存储空间，于是原本看似充足的存储空间，转眼间就变得捉襟见肘

3.1.2 ZeRO – solving the memory overhead issue of DP

用图示表示 16 倍内存消耗时，你会发现，至少在参数内存层面，Adam 优化器的状态数据才是真正的内存占用大户，内存消耗量实际上取决于优化器状态占用的字节数，这部分内存开销通常甚至会超过核心参数和梯度本身所占用的内存

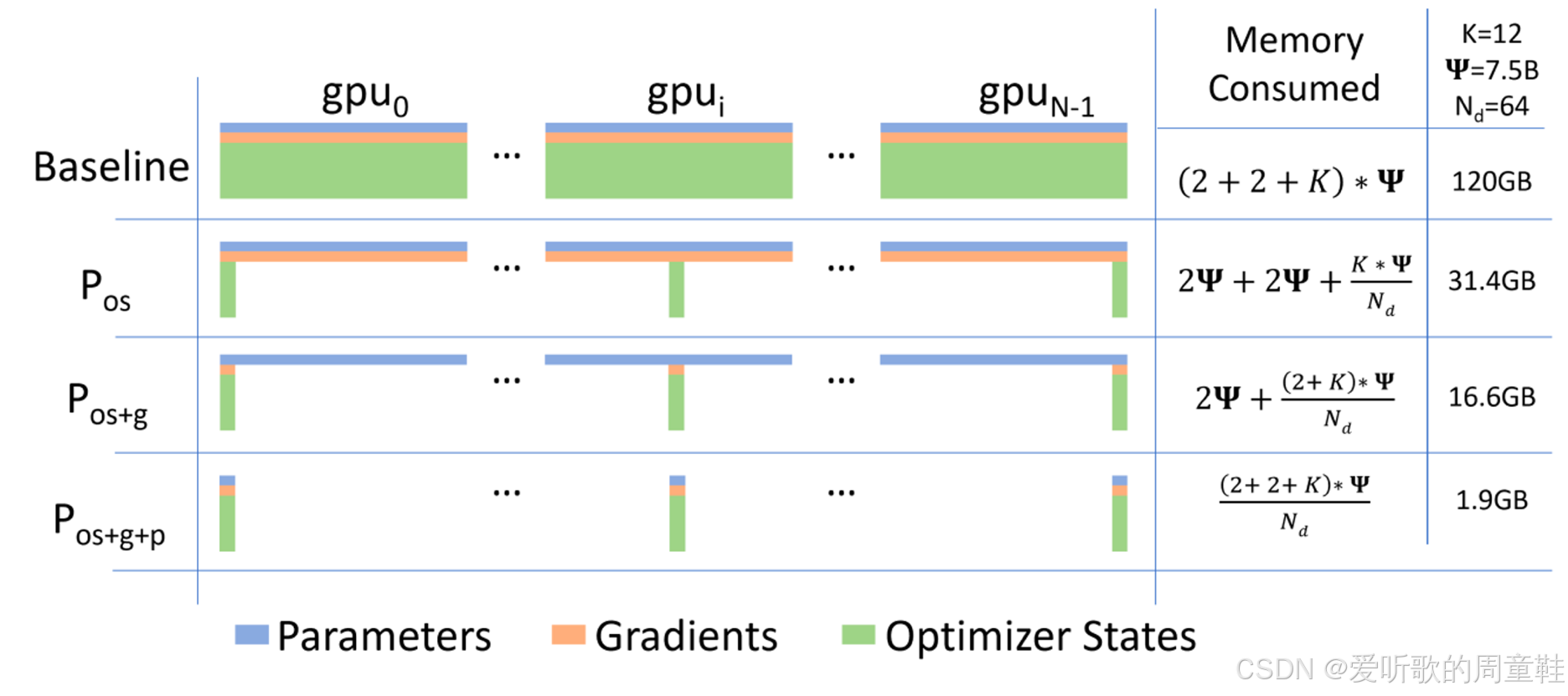
举个简单例子，当 75 亿参数的模型分布在 64 个加速器上时，内存消耗量会变得极其惊人，内存消耗会随着 GPU 数量呈线性增长，这显然不是理想的情况，但当我们分析这个情况时，就能发现几个显而易见的解决思路

你可能会产生一个疑问，为什么需要在不同设备间复制参数和梯度？这似乎是数据并行的必要操作，但优化器状态真的需要在每台机器上都保留吗？当提出这个疑问时，或许就能理解第二行方案的精妙所在

这种方案被称为 优化器状态分片，若能实现这种优化，仅此一项就能将总内存占用量从 120GB 降至 31.4GB，进一步对梯度进行分片处理后，内存占用量还能压缩到 16.6GB，倘若连模型参数也实施分片，内存消耗最终可降至惊人的 1.9GB，至此我们便实现了理想状态，通过全面分片处理，已将优化器状态、参数及梯度所需内存彻底优化

3.1.3 ZeRO stage 1. optimizer state sharding

正如刚才提到的，我们将采用优化器状态分片方案，现在，一阶矩和二阶矩已分散存储在所有 GPU 上，但所有节点都完整保留了模型参数和梯度数据，这为何至关重要呢？

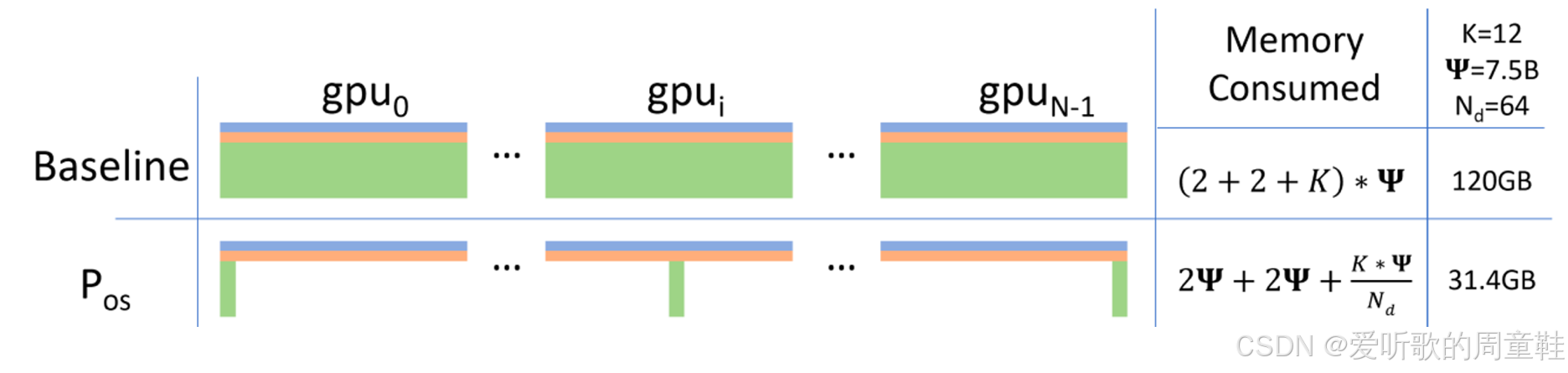
假设我们是 GPU 0 号节点，虽然我持有完整的参数和梯度数据，这些数据确实足以让我计算出完整的梯度，这个示例中的完整梯度更新确实可以计算得出，唯一无法实现的是：我们无法直接利用该梯度执行原子级更新操作，若无法获取全部优化器状态，则无法完成参数更新，这正是核心所在

GPU 0 会计算所有参数的梯度，但它仅负责更新自身持有的参数分片，这正是关键所在。我们将分布式执行参数更新任务，随后我们将同步回传更新后的参数，下面我们将详细展示这个过程的实现机制，并解释为何称其为零开销

第一步，假设每个 GPU 获取不同的数据点，为方便理解，我们将简化整个批次计算过程，假设我们使用 GPU 0 到 GPU 3 共四个计算单元，每个 GPU 处理一个独立样本，并基于该样本计算完整梯度

接下来，我们将对这些梯度执行归约分散操作，具体来说，我们将汇总各个 GPU 持有的梯度数据，从某种意义上说，就是收集每个 GPU 计算得到的梯度分量，假设由 GPU 0 负责处理参数的第一部分（约前 25%）

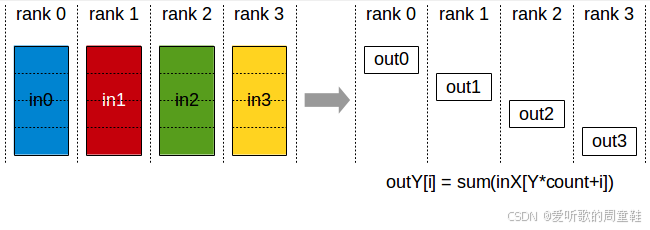
如上图所示，纵轴表示参数分布，横轴对应各个 GPU 的编号，我们将通过归约分散操作确保 GPU 0 能获取所有其他 GPU 针对其负责参数子集计算的梯度信息。此时，GPU 0 将接收来自 GPU 1、GPU2 和 GPU 3 的梯度数据，并通过归约操作将这些数据整合到自身

此时，GPU 0 已获得更新自身参数所需的全部信息，因为它持有与第一部分相对应的优化器状态，它已获得该部分完整的梯度求和结果，此时，它将利用梯度及优化器状态对自身负责的参数部分执行梯度更新，至此，GPU 0 已完成该参数子集的完整更新，接下来只需通过全聚集操作将所有更新后的参数同步至所有计算节点，如下图所示：

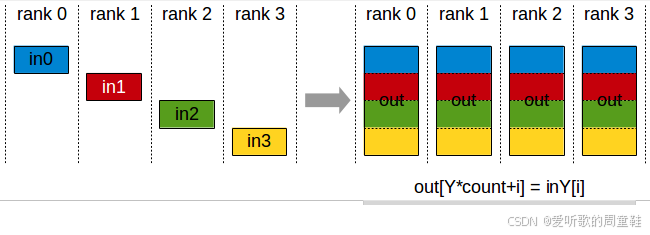
正如我们之前提到的，归约分散加全聚集的组合操作，其通信成本与全归约操作是等价的，这里出现了一个精美的计算魔法：虽然之前我们需要对所有梯度执行全归约操作来确保各节点的同步，但现在这个操作的通信成本是参数量 2 倍

但如果我们巧妙设计更新方式，就能将操作拆解为归约分散和全聚集两个步骤，并在两步之间插入计算任务，这种设计在保持总体通信计算成本不变的同时，实现了优化器状态在整个模型中的完全分片存储，因此在带宽受限的场景下，零冗余第一阶段（ZeRO stage 1）实际上实现了零通信开销，同时显著降低了内存占用

3.1.4 ZeRO stage 2. the simple extension to gradient sharding

我们将逐步构建，最终实现更复杂的 ZeRO 第三阶段，ZeRO 第二阶段仍然相对简单，希望现在大家对优化器状态分片技巧的理解更清晰了，现在我们需要进一步扩展分片范围。我们计划将梯度数据在多个计算节点间进行分片存储，大体上，我们可以采用与第一阶段类似的处理技巧，但这里存在一个额外的复杂性

那么，这个额外的复杂性究竟是什么呢？问题在于，我们永远无法实例化完整的梯度向量，一旦执行完整的反向传播计算，试图生成完整的梯度向量时，很可能会引发内存溢出问题，因此，我们希望将内存占用的上限严格控制在以下范围内：完整参数 + 分片梯度 + 分片优化器状态

这就意味着在进行反向传播计算时，我们必须采用这样的策略：在计算梯度向量过程中，不能先生成完整梯度再进行通信传输，我们需要在反向计算梯度的过程中，每当计算完一层的梯度就必须立即将其发送到对应的 GPU 设备上

具体实现原理如下：其核心理念基本相同，此时每个计算单元都持有各自对应的批次数据分片，所有计算单元开始沿着计算图逐步执行反向传播。假设我们现在要逐层进行操作，各神经网络层被原子化地分片到不同 GPU 上，因此，在沿计算图执行反向传播时，我们将在计算完某层的梯度后立即调用归约操作，将这些梯度发送至对应的工作节点。

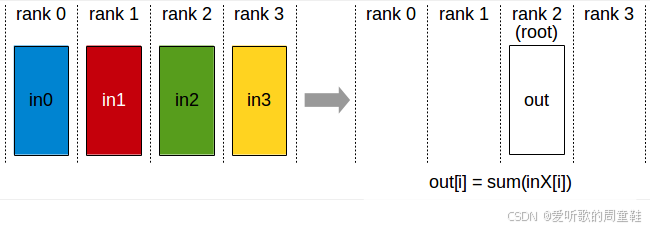
每个神经网络层都归属于特定的工作节点，在本例中可能归属于 2 号 GPU，此时我们将立即执行归约操作，将数据发送至对应工作节点，此时梯度数据即可释放，无需在 0 号、1 号和 3 号计算节点上存储这些梯度数据，因此可以立即释放这部分内存

随后我们将继续执行这一流程，至此所有计算节点都已完成梯度数据的全量更新。此时各计算节点已获得对应参数分片的完整梯度数据，各计算节点已持有对应参数分片的完整优化器状态，各计算节点可独立更新其负责的参数分片，随后通过全聚集操作将参数重新聚合

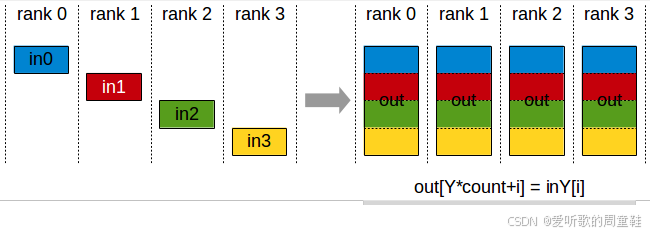
表面看来通信开销似乎更大，因为需要对每个网络层都执行这种归约操作，但这仅涉及少量参数的通信传输，数据已分片，因此总体通信量仍保持不变。ZeRO 第二阶段会产生额外开销，因为需要逐层同步，并确保梯度准确分发至对应工作节点，但这类开销其实微乎其微，整个机制依然简洁明了，实现起来相当直观

3.1.5 ZeRO stage 3 (aka FSDP)

最后要介绍的是：ZeRO stage 3，第三阶段确实更为复杂，但它能带来最大的收益，此时所有要素（内存占用、计算负载等）基本上都能按照 GPU 数量实现线性归约，这样就能实现最大程度的内存优化

你可能听说过 FSDP（全分片数据并行），甚至之前已经在某些场景中使用过这项技术，FSDP 本质上就是 ZeRO 第三阶段的实现，希望通过这次的讲解，你能真正理解 FSDP 的工作原理

这个原理同样适用，我们将对所有数据进行分片处理，包括模型参数在内，我们将采用于 ZeRO 第二阶段相同的策略：通过渐进式的通信与计算，避免在内存中保留庞大的梯度向量

我们将在执行计算图的过程中（包括前向传播和反向传播），按需发送和请求参数，在整个计算过程中，我们将采用按需传输的方式传递数据，当然，关键在于尽可能低的开销实现这一过程

FSDP 真正令人惊讶之处并不在于这种技术可以实现，而在于它能够以相对降低的开销实现

上图完整诠释了 FSDP 的核心原理，我们的具体实现是：在运算过程中，模型权重会通过全收集操作进行同步，因此对于每个网络层而言，任何单个 GPU 都不会存储完整的参数集。

这就意味着，我们无法像常规做法那样直接对 GPU 0 发出指令：“现在开始执行前向传播”，这种传统方式在此场景下无法实现，以 GPU 0 为例，它仅存储着神经网络最底层的参数，当 GPU 0 完成该层的计算后，就会暂停运算，并向所有其他工作节点发起参数请求，此时计算流程会暂停，执行全聚集操作（all gather）

该操作会汇集所有工作节点的参数，此时它已获取执行前向传播所需的全部参数，于是系统就能继续推进，计算之前缺失的那一层，此时系统便可释放这些权重所占用的内存，这些权重数据已不再需要，现在系统可全聚集下一层的参数，执行新一轮前向传播，完成后立即释放权重内存，如此循环往复，但是必须保留激活值，可以看到上图中激活值占用的内存正在持续增长，这终将成为制约性的瓶颈问题。

但如果我们暂时忽略激活值的问题，这种机制就非常理想：我们加载一个层，执行前向传播，然后立即释放它，此处的内存开销极低，当完成前向传播后，就可以对反向传播执行相同的操作，在反向传播中，每当在神经网络中回退一步时，我们都会全聚集所需的参数，通过执行归约分散操作来更新计算完成的梯度，随后即可释放权重占用的内存，因此，既可以释放不再需要的梯度，也能释放对应的参数内存，最终，我们就能获得一个完成全部参数更新的完整模型

因此，我们需要重点关注以下三类操作，具体而言，我们需要执行全聚集操作，再次全聚集操作，最后通过归约分散操作来完成梯度更新后的模型参数更新。从概念上讲，这只是在 ZeRO 第二阶段基础上增加了一个步骤，但确实会带来更多的计算开销，因此总体通信开销现在变得更大了，此前我们的通信量是参数量的两倍，从某种意义上说，之前的操作几乎不需要额外开销，但现在情况不同了，现在总通信开销达到了参数量的三倍，而且还需要承担等待这些通信操作完成的时间成本

但 FSDP 真正令人惊艳之处在于，它的实际运行开销低得出乎意料，你可能会认为：由于我们不断在请求和来回传输参数，这种看似疯狂的操作会导致运行速度极其缓慢，我们需要持续保持通信，但关键在于实现通信与计算得重叠执行

理想状态是让 GPU 在运算的同时，后台通信就像预加载机制般持续工作，当你需要某块数据时，它早已传输到位，随时可供调用，让我们通过下面这个示例具体说明，这正是让全分片数据并行真正实现高效运行的核心所在

假设我们有一个计算图，其结构为 $(W_1{W}_0+W_2{W}_0)x=y$，假设输入变量为 $x$，这就是一个非常简单的计算图结构，接下来就可以运行全分片数据并行（FSDP）。此时系统会同时执行计算和通信操作，最终会形成下面这样的模块化流程图：

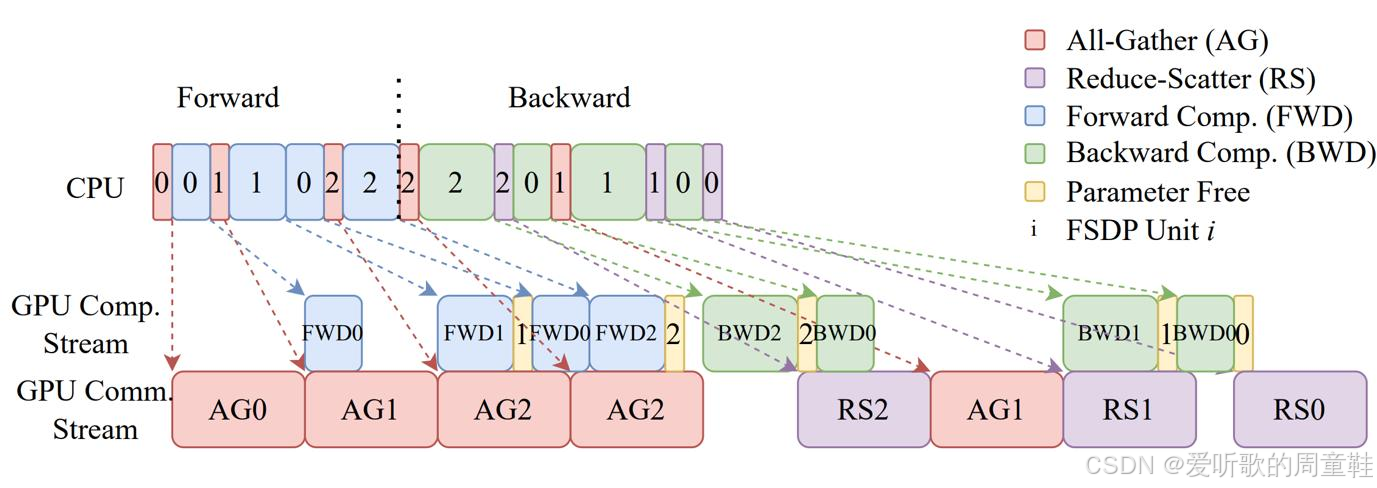
CPU 会批量发现指令，要求 GPU 的通信模块去获取某些参数，CPU 会向 GPU 发送指令：“现在执行矩阵乘法运算”，从某种程度来说，这些指令会大幅领先 GPU 的实际执行进度，上次讲座我们查看性能分析器时已经见识过这种情况了

现在让我们来看看设备上发生的通信与计算的具体执行序列：在最开始阶段，我们必须确保所有设备都获取到了第 0 层（即这里的 $W_0$）的权重参数，于是我们先执行全聚集操作 0（all gather 0），并等待该操作完成，待该操作完成后，我们就能对 $W_0$ 执行前向计算步骤

比如说，我们可以计算 $x\times W_0$，此时，全聚集操作 1（all gather 1）恰好与全聚集操作 0 的结束同步启动，因此在进行矩阵乘法的同时，我们实际上已开始预加载下一组所需参数，当然，通信传输的速度相对较慢，虽然存在些许间隙，但最终完成速度仍远快于初始加载阶段

此时便可执行前向传播 1（forward 1），与此同时，后台进程已开始加载第二组参数，此时我们正在释放与前向传播 1（forward 1）相关的黄色分片参数，此时另一个关键点是：计算过程存在复用，$W_0$ 参数被重复使用了两次，因此无需进行该参数的通信传输，这一过程同样会瞬间完成

在前向传播 2（forward 2）被调用前，其参数早已预载完毕，因此这里不会出现计算空泡（bubble），随后便可释放第二组（number 2）参数，至此便完成了整个前向传播过程。可以看到图中的间隙相对较小，我们成功在计算需求产生前完成了大量数据的预加载，通过这种巧妙的预请求排队机制，在实际需要数据前就提前发起等待请求，能有效规避大量通信开销

此时进行到前向传播阶段 2 时，我们已完成了整个前向计算过程，此时便可释放权重 2 所占用的内存，随即启动反向传播过程，可以看到，反向传播所需的全聚集操作 2 早已提前完成，因此可以立即启动反向传播 2 和反向传播 0 的计算，权重 0 已预先存储就绪，至此已完成准备工作

此时反向传播阶段会出现较高的计算开销，因为需要执行归约分散操作（reduce scatter），接着进行全聚集操作（all gather）等一系列通信步骤。相信看到上面这个示意图你会惊叹：尽管我们采用了如此彻底的分片策略，实际出现的计算空泡（bubble）也在可控范围内，通信带宽几乎得到充分利用，计算流程也没有出现长时间的停滞，这说明我们确实实现了对现有资源的高效利用，这个结果相当不错

3.1.6 What’s the point?

这其实就是分布式数据并行的实现方式，ZeRO（零冗余优化器）正是实现高效分布式数据并行的关键技术。具体来说，ZeRO 技术分为不同优化阶段：

第一阶段（Stage 1）基本不会产生额外开销，该阶段采用与基础数据并行相同的通信模式，同时实现了优化器状态的分片存储，这种做法优势显著，值得全面推广。零冗余优化器第二阶段（ZeRO Stage 2）的内存占用仅为参数量的两倍，虽然总带宽消耗保持不变，但在反向传播过程中逐步释放梯度，会引入额外的计算开销。零冗余优化器第三阶段（ZeRO Stage 3）的实现更为复杂，虽然通信开销增至三倍，但整体影响仍在可控范围内

因此即便在网络连接速度较慢的情况下，人们仍然会采用数据并行的方式，这种方法的实现理念也极为简明。数据并行尤其具备一项显著优势，对模型架构的适应性很强，在之前的讨论中，我们完全没有涉及如何具体实现 transformer 架构的内容，这些讨论都停留在高度抽象的层面，这正是全分片数据并行（FSDP）广受欢迎的原因之一，只需编写一个封装器就能实现任意神经网络的并行化，无需深入理解或剖析架构的具体工作原理

以下是一些具体案例：

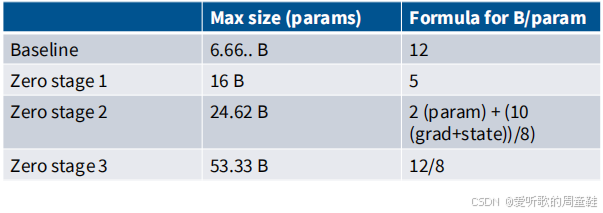
可以看到在配备八块 A100（80GB 显存）的计算节点上，我们能运行的最大模型规模以 baseline 为例，最终可能勉强塞得下 60 亿参数的模型，而如果采用 ZeRO 第三阶段方案，就能容纳约 500 亿参数规模的模型，模型容量上限获得了显著提升

3.1.7 Issues remain with data parallel – compute scaling and models don’t fit

数据并行中存在一个关键资源问题，这里有个重要概念需要你特别留意，并行批处理规模实际上是一项极其关键的资源指标，其核心限制在于：并行度无法超过批处理规模本身。这是因为每台机器最多只能处理一个样本实例，每台机器无法处理不足一个的样本片段，这意味着当批处理规模达到上限时，数据并行方案将无法继续扩展，而增大批处理规模带来的收益会逐渐递减

在第一次作业中，大家可能已经尝试过调整不同的批处理规模，应该已经发现，当批处理规模超过某个临界值后，优化效率的提升幅度会迅速衰减。关于这一现象已有大量研究文献，OpenAI 曾发表过一篇关于 “临界批处理规模” 的经典论文 [McCandlish+ 2018]

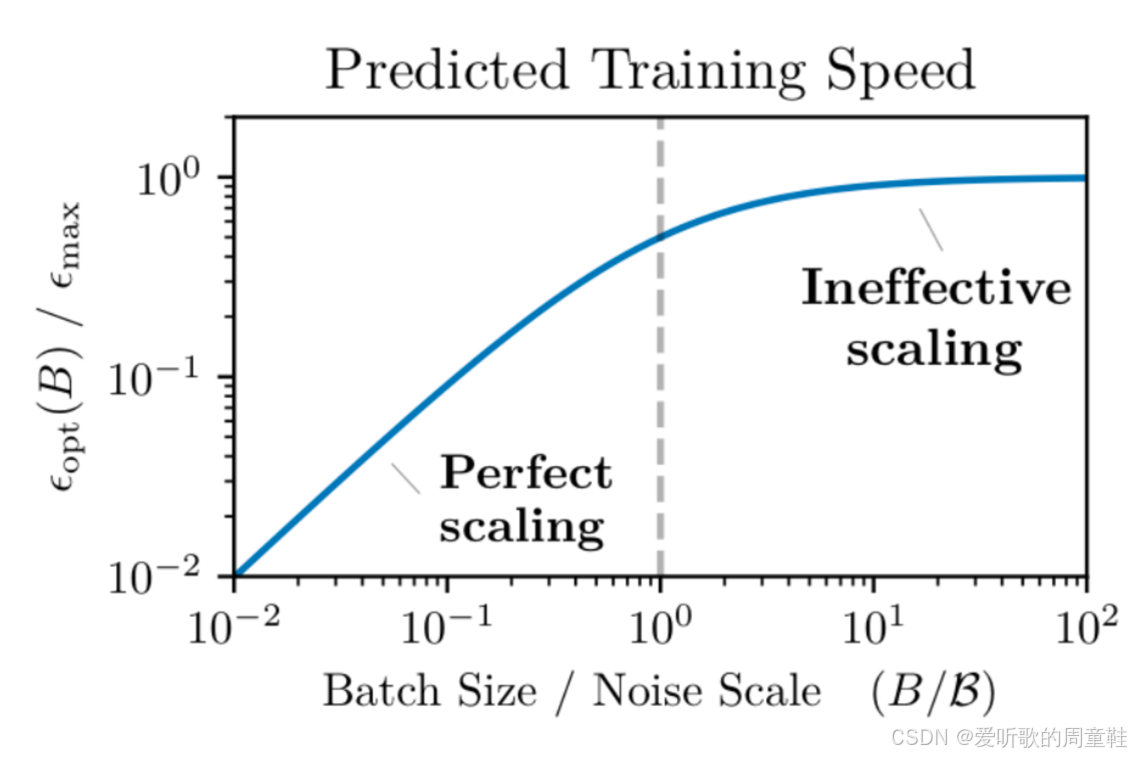
其核心观点是：当批处理规模超过特定阈值后，每个新增样本对模型优化效果的边际贡献会急剧下降，直观来看，当批处理规模低于某个临界值时，梯度噪声较为显著，此时增大批处理规模能有效降低噪声，带来显著收益，但当规模超过临界点后，优化效果主要受限于梯度更新次数而非方差归约效应

这意味着单纯靠数据并行无法实现无线扩展的并行训练能力，批处理规模本身就是一项关键资源，本质上，我们拥有一个固定的最大批处理规模上限，可以通过不同方式来分配使用这一资源，这一点我们会在后文详述

因为其他类型的并行技术同样能从更大的批处理规模中获益，因此需要将批处理规模合理分配到不同计算环节，但数据并行方案仍存在固有缺陷，ZeRO 第一、第二阶段技术无法实现内存占用的线性扩展，ZeRO 第三阶段虽然理论设计精妙，但实际运行时可能存在性能瓶颈

更关键点的是，这与先前的问题直接相关，该项技术并未降低激活内存的占用，理想情况下，应该将模型完全分割并独立存储，这样才能同步降低激活内存的占用，因此当前急需更高效的模型分割方案，以便将这些超大规模模型适配到 GPU 显存中

3.2 Model parallelism

这就将我们引向了模型并行技术，我们需要在不改变批处理规模的前提下实现内存扩容，我们还需要寻找新的并行化维度，无需依赖大批量数据也能实现高效并行计算的解决方案

为此，我们将采用参数分片方案，把模型参数分布式部署在多个 GPU 上，从某种角度来看，这类似于零冗余优化器第三阶段（ZeRO stage 3）的实现原理，但我们不再进行参数通信，我们将改为传递激活值，这种设计将带来本质性的改变，有时激活值会被参数小得多，这对我们非常有利

我们将介绍两种不同类型的并行方式：

• 1. Pipeline parallel
• 2. Tensor parallel（+ Sequence parallel）

我们将先讲解流水线并行，这个概念上更简单，但实现起来相当棘手，再介绍张量并行，这个概念或许不够直观，但实现起来更为优雅，也是目前更主流的方案，这两种方式分别对应着模型切分的不同维度

3.2.1 Layer-wise parallel

流水线并行可能是分割神经网络最直观的方式，众所周知，深度神经网络是由多个层级构成的，既然网络由多个层级组成，最自然的切分方式就是沿着层级边界进行划分

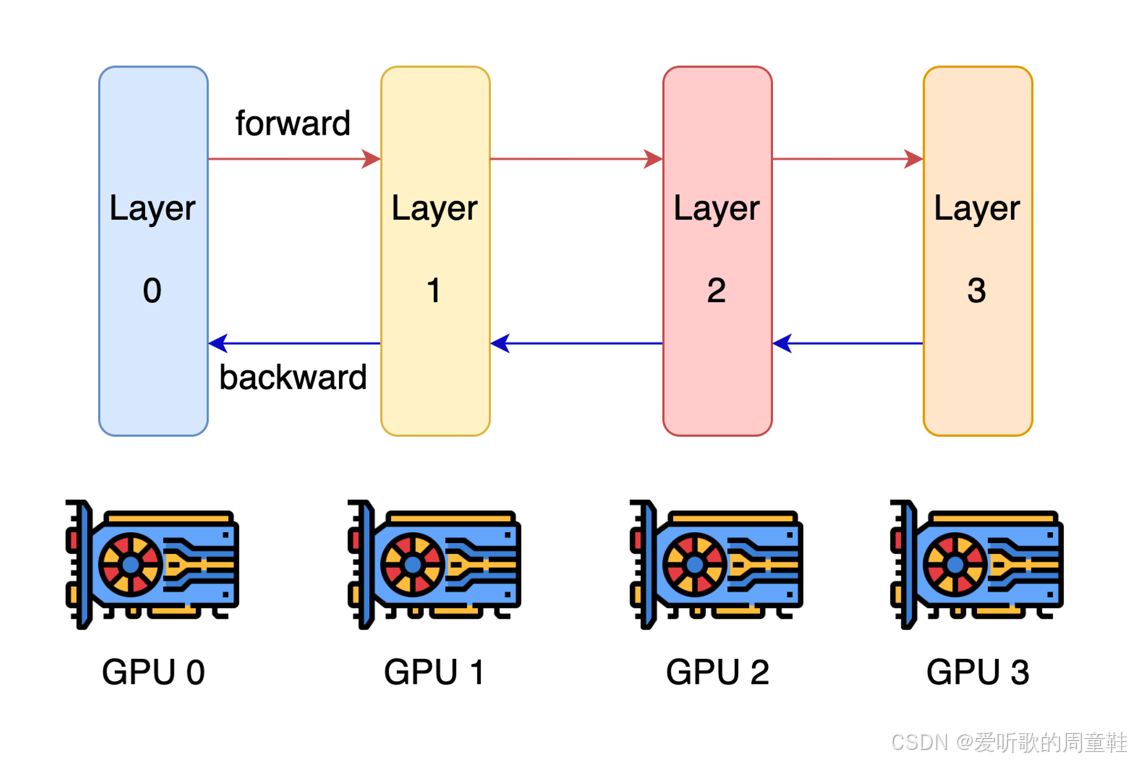
因此，每个 GPU 将负责处理部分网络层，并通过传递激活值来实现协同计算，在这种模式下，每个网络层都专属分配给特定的 GPU，GPU 之间将通过相互传递激活值来实现数据流转，而在反向传播过程中，梯度数据将以相反方向从 GPU 3 逐级回传至 GPU 0

这种设计确实精妙，但它存在一些潜在问题，显然，大家应该能注意到：大多数 GPU 在大部分时间都处于闲置状态，这种资源利用率确实相当不理想。因此，如果我们采用之前描述的那种简单并行方案，比如让每个层独立进行前向传播，假设只处理单个样本，最终得到的工作流程示意图就会呈现下面这种状态

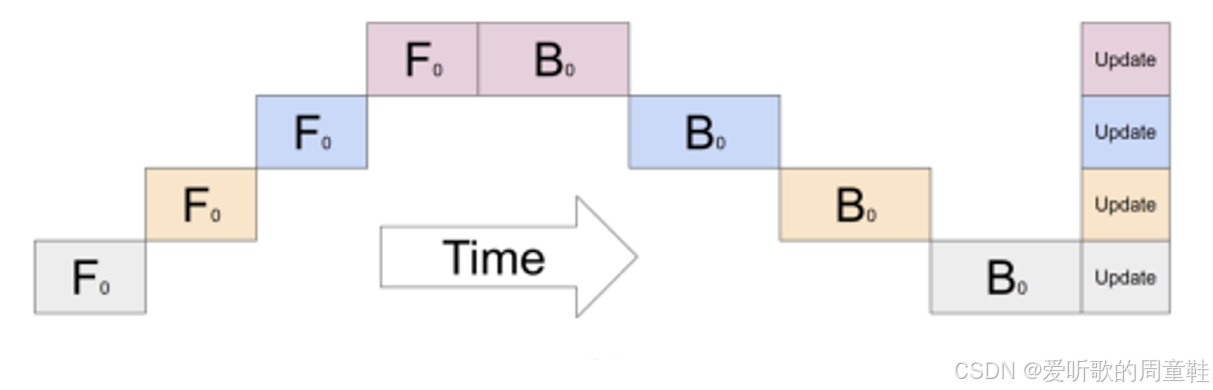
图中每一行代表不同的神经网络层，同时也对应着不同的 GPU 设备，横轴代表时间流动方向，从左到右推进，你观察到了什么现象？首先，我们在最左侧这里计算第一层，随后，这些激活值会传递到第二层进行处理，GPU 2 被唤醒后进入工作状态，就像在说：“好了，现在轮到我了”

GPU 2 完成计算后，将数据传递给 GPU 3，继而流转至 GPU 4，此时反向传播流程启动，如此循环往复。我们这里看到的现象，就是业界常说的 “计算气泡”，这种巨大的计算空泡意味着系统存在严重的资源闲置开销，可以看到，GPU 的有效利用率仅为 $\frac{1}{n}$

从某种角度来看，这堪称最糟糕的并行方案，虽然增加了 4 块 GPU，但实际吞吐量却与单块 GPU 无异。于是我们可以采取更智能的解决方案：构建一个流水线处理系统，我们不再简单地按网络层进行切割，而是构建一个处理序列，让每块 GPU 依次能处理特定计算任务

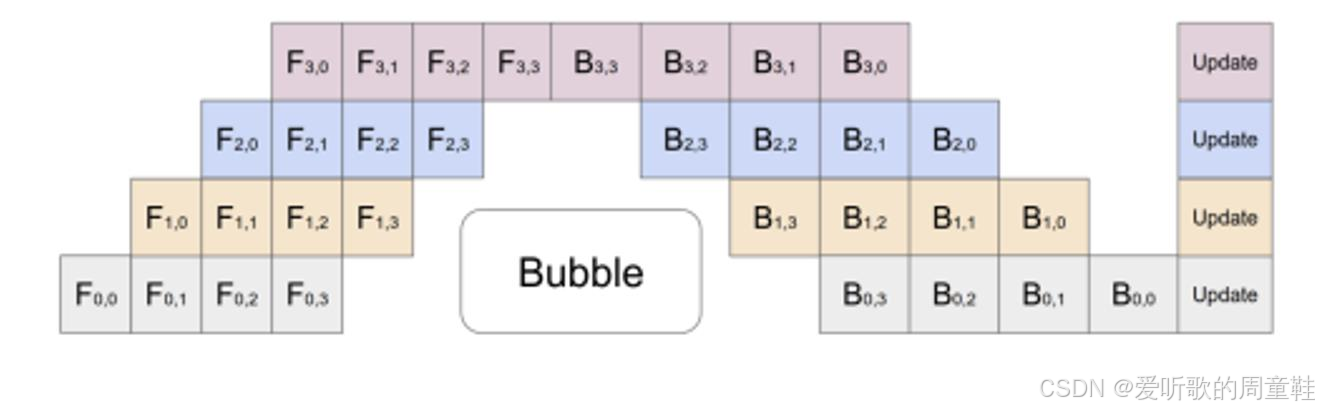
现在假设我们有一个微批次数据，因此每台机器将处理四个样本，我们的处理策略是：一旦完成第一个样本（即首个数据点）的计算，就立即将其激活值发给第二块 GPU，紧接着就能立即开始处理第二个数据点，如此一来，通信与计算就实现了重叠执行，第二块 GPU 可以开始运行，而第一块 GPU 仍继续工作

通过增大批次规模，现在有可能进一步缩小空虚时间窗口，现在大家应该能理解为何我们之前将批次规模称为一种资源了。在固定批次规模的条件下实施流水线并行时，既可以利用该批次规模来缩小流水线空闲间隙，也可以将其用于数据并行处理，这本质上是一种资源分配的取舍选择，因此，你可以通过多种方式将单个批次规模拆分成不同的组合形式

微批次规模的大小将直接影响流水线空闲时间的长度，实际上，系统开销与有效计算量的比值可表示为 $\frac{n_{stages}-1}{n_{micro}}$，也就是流水线阶段数减一再除以微批次数量。因此，当采用超大批次规模时，流水线并行技术有望实现更高效率，但正如前文所述，实际应用中的批次规模始终存在上限，我们无法将批次规模无限制地提升至任意数值

3.2.2 Why pipeline parallel?

总体而言，流水线并行技术的表现看似极不理想，那我们为何仍要采用这种方案呢？既然存在计算效率损失，为何我们仍要承受这种 “气泡” 代价来实现并行化？

这主要基于以下考量：相较于数据并行，流水线并行能显著节省内存开销，ZeRO-3 阶段会对参数进行分片，但流水线并行还能对激活值进行分片，这是其独特优势。流水线并行还具备优异的通信特征，其性能仅取决于激活值，同时它还采用点对点通信机制，因此根据网络拓扑结构和具体配置情况，流水线并行可能特别适合处理网络中通信较慢的区域

因此，流水线并行技术通常适用于网络中的低速链路场景，无论是节点间通信，还是跨机架甚至跨数据中心的场景皆适用

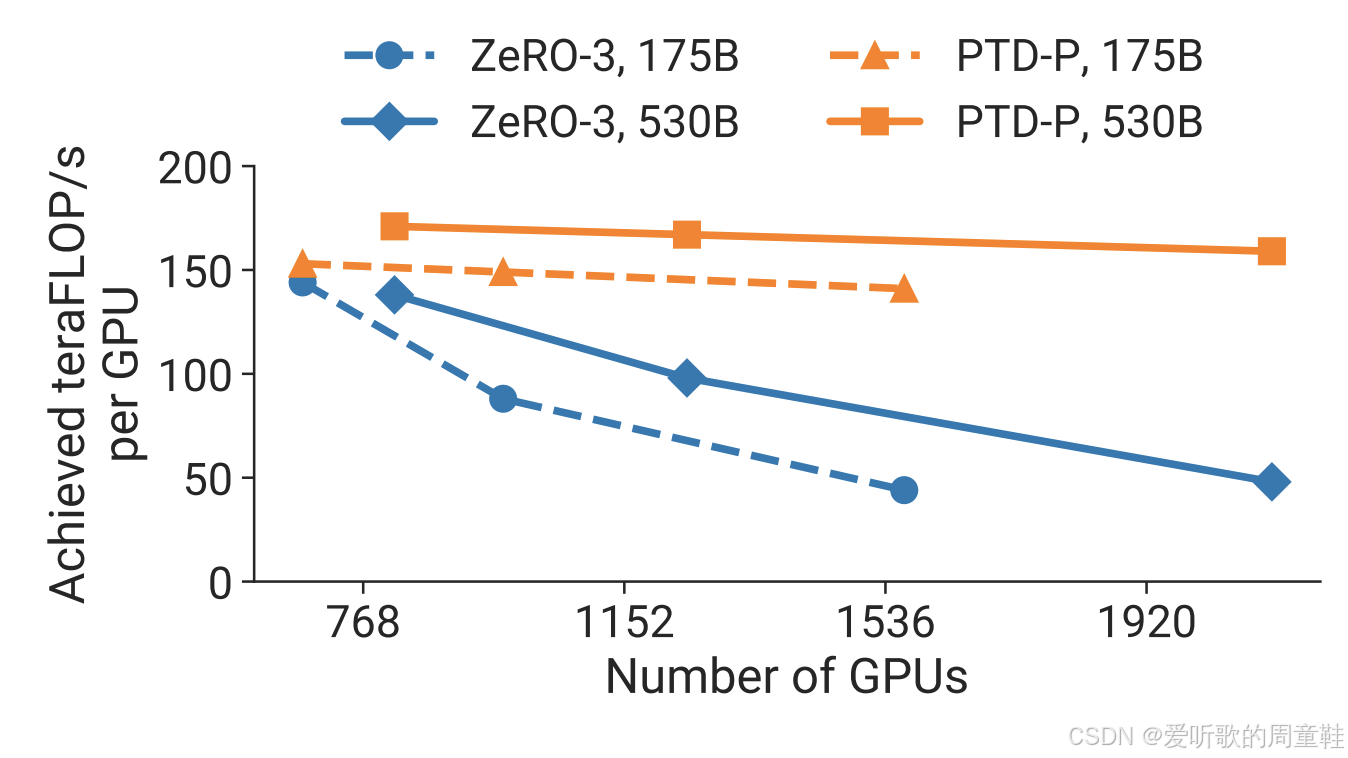
下图是来自 NVIDIA 论文中的一个示例：

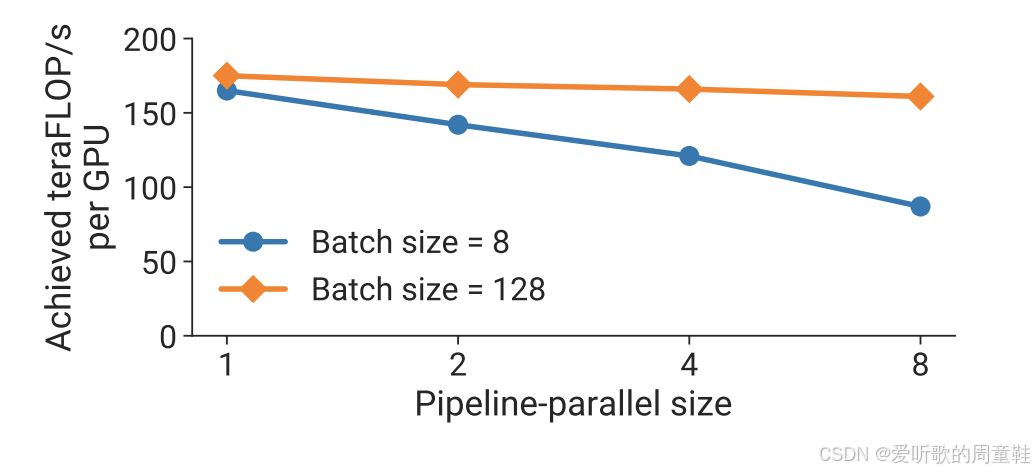
稍后我们会更详细地讲解这篇论文，他们的研究非常出色，清晰地展示了各类并行计算的性能特征，但当批处理大小（batch size）设为 8 时，随着流水线并行规模和设备数量的增加，每个 GPU 的利用率会出现明显下降，而如果将批处理大小大幅提升至 128，即使采用规模可观的流水线并行，也能保持相当不错的利用率，因此批处理大小对于掩盖计算开销气泡至关重要，否则就会出现性能问题

3.2.3 ‘Zero bubble’ pipelining

当然，可以采用多种不同的流水线并行策略，而不是采用这些标准模式来调度气泡间隙，可以将计算任务拆分为更精细的片段，将不同阶段的工作分配给不同设备，让各个子层在不同设备上执行，并在不同分区进行差异化计算，这样就能实现更优的流水线交错执行

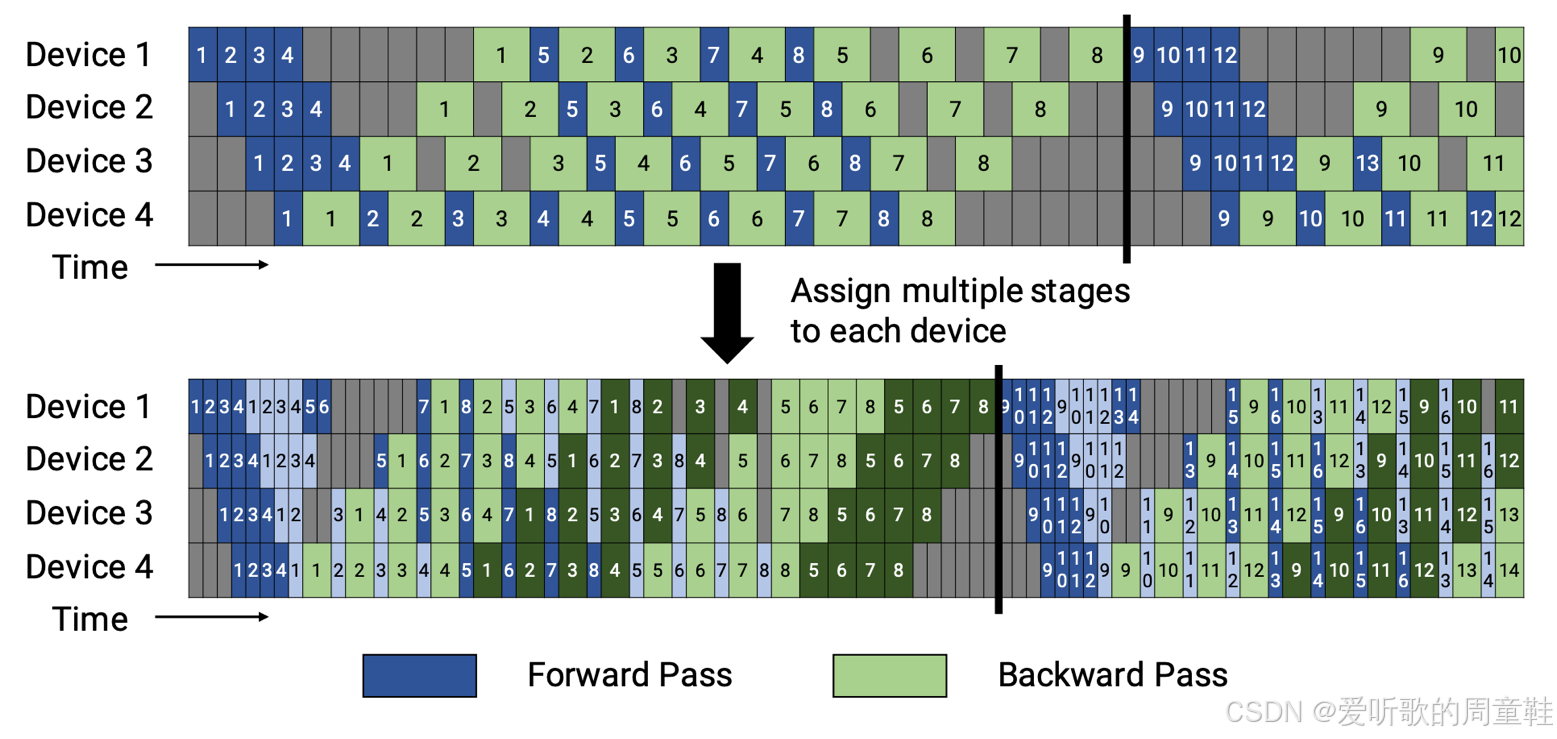
接下来我们来重点介绍一个非常精妙的进阶版本—零气泡流水线并行（zero bubble pipeline），在 DeepSeed 框架中他们将其称为 dual pipe，但其核心技巧如出一辙。设想这样一个场景：当我们在执行反向传播计算梯度时，这个过程可以拆解为两个独立环节：首先是激活值的反向传播环节，当沿着残差连接向下传递时，本质上需要计算激活函数对应的导数，而当抵达参数节点时，还需同步计算梯度本身，这是要解决的是参数如何更新，而不仅仅是激活值相对于前一层的变化

举个具体例子，请看下面的示意图：

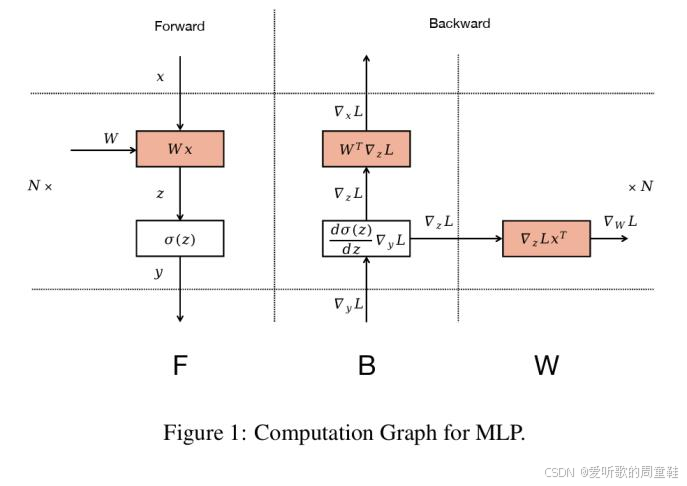
这张图展示的是前向传播过程，这是一个简单的多层感知机（MLP），这里进行的是权重乘法运算，接着执行非线性变换，最终输出的是经过非线性变换的结果，这就是 MLP 中最基础的单个计算单元。

现在来看反向传播过程，我们持有关于损失函数的梯度，这样就能计算出这些梯度将如何改变 MLP 的输入 x 值，从某种意义上说，这就是该层激活函数的梯度，在计算这些梯度的同时，自然就能用它们来推导出更新权重所需的梯度

但关键在于计算权重梯度的这个环节，这个计算可以随时进行，这部分计算不存在时序依赖，因此，我们可以将这个计算重新调度到计算图的任意位置，对于存在串行依赖的部分可以采用标准的流水线并行方式处理，但凡涉及参数更新的计算都可以根据需要重新调度到任意计算阶段

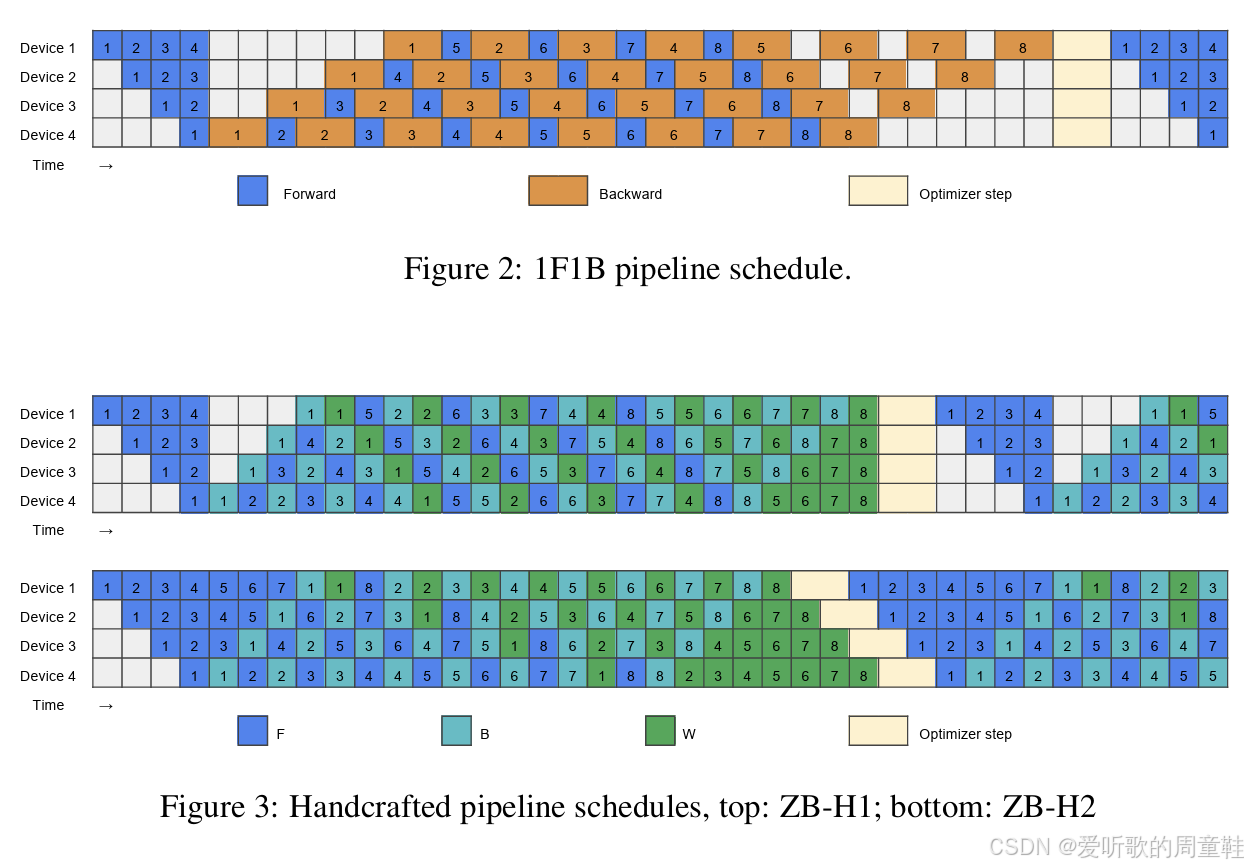
核心思路是：首先构建一个标准的 1F1B（前向-反向）流水线架构，这种优化方案能有效减少计算气泡（空闲等待时间），随后可以在此基础上进行扩展优化，我们可以将其拆解为两个部分：B（反向传播计算环节）和 W（权重梯度计算环节）

现在，我们可以在原本存在计算气泡的位置执行权重梯度（W）的计算，原本处于空闲状态（图中白色部分）的计算资源现在都可以被权重梯度计算（W）充分利用。通过仔细分析计算任务间的串行依赖关系，我们最终实现了 GPU 计算资源的高效利用，这正是精心设计并行策略带来的显著优势

必须承认，这套并行机制的实现复杂度极高，若要以这种方式实现流水线并行就必须介入自动微分系统的底层计算逻辑，必须建立一个队列系统来精确追踪数据的流向，流水线并行在基础层面的实现非常复杂，表面看似简单，若有兴趣，大家可以自己动手实现试试，复杂度会呈指数级攀升

3.2.4 Tensor parallel

说到这里，我们正好可以转向另一种模型并行方案，这种方案实现起来要简单得多，这种方案已被众多框架广泛采用，甚至成为许多训练实践中的标准配置，绝大多数超大规模模型都高度依赖甚至完全基于这种模型并行方案，那么，我们还能采用哪些模型切分方式呢？

细想之下，矩阵乘法其实构成了我们大部分的计算工作，在大规模模型中，矩阵乘法占据了绝大部分计算量，绝大多数参数都以矩阵形式存在，通过矩阵乘法参与运算。那么，我们该如何处理这些矩阵运算呢？若能实现矩阵乘法的并行，就能取得显著效果，张量并行的核心思想是：将大型矩阵拆分为多个子矩阵进行分布式乘法运算

假设有一个矩阵乘法运算，给定输入矩阵 X，通过 X 与 A 相乘得到输出矩阵 Y，此时我们可以将矩阵 A 沿列维度切分为 A1 和 A2，同时将输入矩阵 X 沿行维度对半切分，通过分别计算子矩阵乘积 X1A1 和 X1A2 后求和，最终仍能得到完整结果 Y

从概念上讲，流水线并行是沿着网络深度维度（即层级方向）进行切分的并行策略，而张量并行（即当前讨论的这种）则是沿着矩阵乘法的宽度维度进行切分，因此我们可以将矩阵分解为若干子矩阵，然后通过部分求和的方式完成计算

下面是一个在多层感知机（MLP）中实现该策略的典型示例：

在这个方案中，每个 GPU 负责处理大型 MLP 矩阵乘法中的不同子矩阵块，随后我们将通过集合通信机制在需要时对各个计算节点的激活值进行同步，那我们具体要怎么做呢？

上图多层感知机（MLP）的结构中包含两条并行路径，上半部分和下半部分各自形成独立的数据通路，这些操作将矩阵进行了分块处理，现在要实现这个运算：$Y=GeLU(XA)$，现在我们要将矩阵 A 拆分成 A1 和 A2 两个子矩阵，然后在右侧计算，对 $YB$ 进行 dropout 操作，最终将结果作为 Z 返回，因此我们也需要对矩阵 B 进行分块处理

现在我们已经把两个大型参数矩阵 A 和 B 都拆分成了两部分，在前向传播过程中，我们会将输入 X 复制两份进行处理，这样每个 GPU 都能获得相同的输入数据副本，然后我们将分别使用 A1 和 A2 对这些输入数据进行运算

它们的行维度是相同的，因此在这些数据上进行运算是完全可行的，XA1 和 XA2 将分别生成激活值 Y1 和 Y2，这些结果将分别输入到 B1 和 B2 中，然后将执行全归约（all reduce）操作对它们进行求和，最终得到结果 Z

在反向传播过程中，梯度会沿着计算图逆向流动，其数据流向与前向传播恰好相反，图中 $g$ 将作为单位矩阵存在，现在我们要把导数同时复制到两侧，然后沿着整个计算图逆向执行反向传播运算，当计算推进到 $f$ 时，由于两条路径的导师在此汇聚，这里需要进行全归约操作，最后将这些梯度求和归并

因此，$f$ 和 $g$ 在这里充当了同步屏障的作用，在前向传播过程中，我们执行了一次全归约操作，而在反向传播中，我们同样执行了一次全归约操作，只不过它们发生在计算图中两个不同的位置，现在你应该能理解这种方法的精妙之处了，只要遇到矩阵乘法运算，就可以将矩阵切分后分配到不同设备上并行计算

正如你可能想到的，这种操作实际上开销不小，每层神经网络都设有一个同步屏障，在前向传播和反向传播过程中，每次都需要传输两次激活值，包括残差激活值在内的所有数据，因此，张量并行这种看似简单的思路，实际上需要依赖超高速的互联网络

有个简单易记的经验法则：张量并行通常只在单个计算节点内实施，比如一台搭载 NVIDIA GPU 的服务器，通常会配备八块共处同一机箱的 GPU，这些 GPU 之间通过超高速互联通道相连，能够实现极高速的通信，因此采用张量并行这类方案就非常合理，这种方案对八块设备间的通信带宽要求极高，因此通常的做法是：张量并行最多应用于同一台机器内的八块 GPU，这样才能将性能损耗降到最低

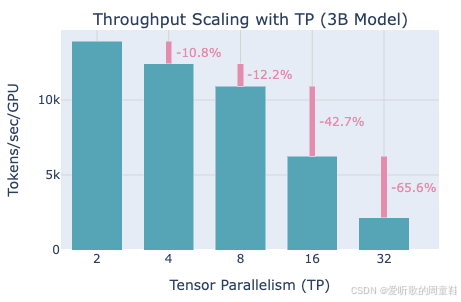
这正是 Hugging Face 并行化教程中的示例，展示了不同级别张量并行下的吞吐量衰减情况，可以看到，采用张量并行会导致 10% 到 12% 不等的吞吐量损失，但在 8 块 GPU 以内，这个程度的性能损耗或许尚可接受，这本质上是为了实现更优并行化所必须付出的代价，但当扩展到 16 块设备时，性能竟会出现惊人的 42% 断崖式下跌，当规模扩大到 32 块设备时，吞吐量会再次暴跌 65%

因此通过可视化数据可以清晰看出，张量并行的最佳实践是控制在 8 块设备以内，这确实是性能拐点，毕竟现有硬件互连架构的物理限制就摆在那里

那么与流水线并行方案相比，当前方案的优劣如何呢？与流水线并行方案相比，我们终于摆脱了之前那种令人头疼的计算空泡问题，更秒的是，我们无需再通过增大批量大小来压缩空间，这个痛点终于被解决了，而且张量并行的应用复杂度相对较低，虽然谈不上极其简单，但确实比较友好，你只需要抓住核心：找出那些大型矩阵乘法运算，判断能否将它们拆分到不同设备上执行，这就是全部要诀

前向传播和反向传播的运算逻辑依然保持不变，与实现零开销或双流水线并行这类方案相比，采用这种方法会让你的工作轻松百倍。但缺点在于通信开销会显著增加，在流水线并行中，每个微批次需要进行点对点通信的数据量是批量大小乘以序列长度再乘以残差维度，而在张量并行中，每层的通信量是流水线并行的八倍，且需要进行全归约通信，这可能导致需要处理的通信量极其庞大

因此正如我们之前所说，经验法则是：只有在具备低延迟、高带宽互连的条件下才使用张量并行，根据实际硬件配置的不同，在实践中你会看到 2 到 16 路不等的张量并行方案，在最后讲解时，我们会通过具体案例向大家展示张量并行的实际应用示例

3.3 Activation parallelism

刚才我们讨论的都是内存相关的问题，从某种意义上说，内存是并行计算中至关重要的环节，毕竟我们要训练的都是大型模型，仔细分析内存占用就会发现，其实激活值才是消耗内存的大头

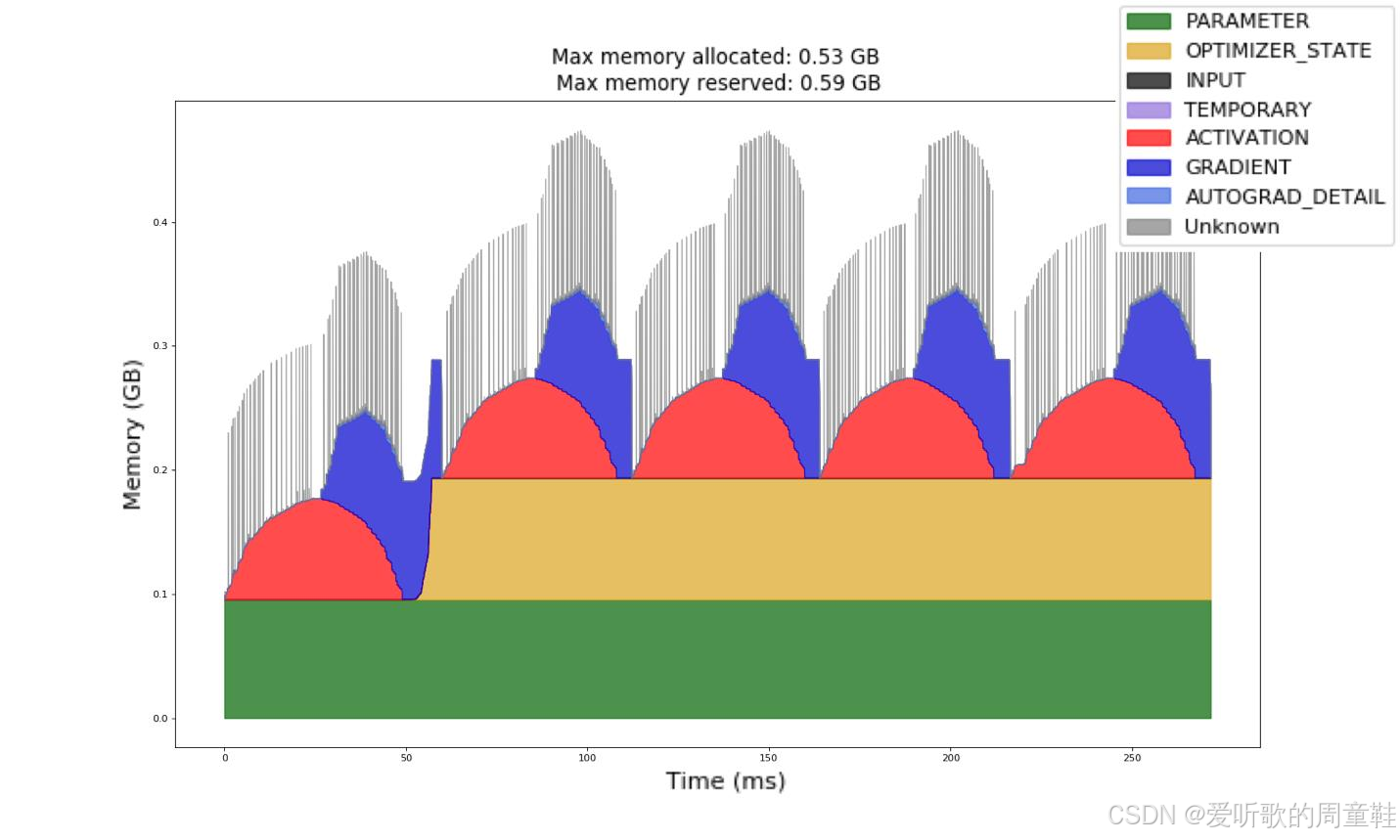
从标准的前向-反向传播过程来看（这个例子出自某个 PyTorch 教程），内存使用呈现出明显的动态波动特征，上面这张图表非常有意思，我们来详细讲解一下

训练过程中参数始终占据着固定内存空间，但在第零次迭代时，优化器状态还未生成，因此实际上，这部分内存占用此时还并不存在。但随着前向传播和反向传播的进行，激活值内存会不断累积增长，当反向传播开始时，激活值内存逐渐释放，同时梯度值开始累积，因此梯度内存占用会随之上升，内存占用的峰值出现在反向传播的中段，此时部分激活值尚未释放，而梯度仍在持续累积

第二次迭代时，内存变化规律与此相同，这张图的核心意义在于：我们已经统筹考虑了所有其他环节，我们已统筹参数、优化器状态和梯度这三要素，但至少到目前为止，我们尚未深入考量激活值的内存占用问题，那么现在就来重点解决这个问题

接下来我们要重点分析的最后一个关键复杂度，就是激活内存问题，张量并行和流水线并行能以线性方式降低绝大多数组件的内存占用，但事实上，这两种方法并不能完全降低所有激活内存的消耗，这里引用 NVIDIA 某篇论文 [Korthikanti+ 2022] 的案例：

该研究专门探讨了如何优化激活内存的使用效率，一个非常有趣的现象是：随着模型规模不断扩大，从左到右，可以看到如果我们采用激进的并行策略，参数和优化器状态占用的内存可以保持不变，但激活内存的占用会持续增长，因为其中某些部分难以实现理想的并行化

因此无论使用多少设备，实际上都无法消除每个设备上激活内存的增长，稍后我们会具体说明原因。不过，如果采用重计算这类更巧妙的方法，就能将激活内存控制在较低水平，这正是并行化某些超大规模模型的关键所在

那么每层的激活内存是多少呢？大家之前应该接触过这类 Transformer 的数学运算和微积分推导，相信现在对这些内容应该比较熟悉了，我们可以计算出每层所需的激活内存量，其计算公式为：

这些数字看似神秘，其实不然，可以清楚的看到，公式由两项组成，左项源自 MLP（多层感知机）及其他逐点运算操作，这部分对应公式中的 $sbh\times 34$，这些数值取决于残差流的维度大小 h

右侧的项展开后实际上就是 $5ab{s}^2$，因为 h 在运算中被约去了，这部分内存需求来自注意力机制中的 softmax 运算及其他二次项计算。当然，若采用 Flash Attention 并配合重计算技术，我们就能大幅削减第二项的数值

那么假设我们采用张量并行方案，我们在所有可行之处都采用张量并行，我们在多层感知机（MLP）、键查询计算以及注意力计算中都实现了张量并行，最终我们会得到类似这样的架构：

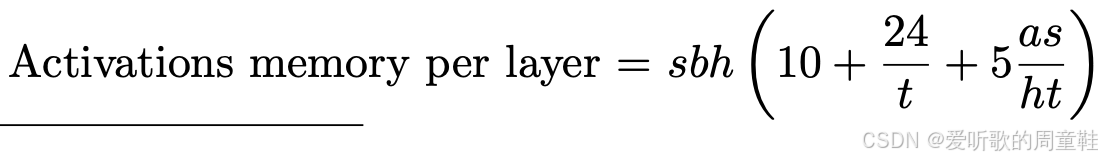
这个架构看起来相当不错，但仍有改进空间，每层激活内存除以 $t$ 即执行张量并行的设备数量，若采用 8 路并行，理想情况下所有激活内存都应归约为原来的八分之一，但你会发现这里存在一个未归约的拖尾项 $sbh\times 10$

细究这些项的本质，它们其实是非矩阵乘法的运算组成部分，像层归一化（LayerNorm）、Dropout 操作、注意力机制的输入以及多层感知机（MLP）的输入，这些运算项都会随着模型规模增长而膨胀，而且它们的并行化效果并不理想，

因此最后需要考虑的是：将这些迄今为止尚未并行的简单逐点运算进行拆分处理，拆分方法其实非常简单：以层归一化为例，序列中不同位置的归一化计算彼此完全独立，这些运算根本不需要考虑其他位置的数据

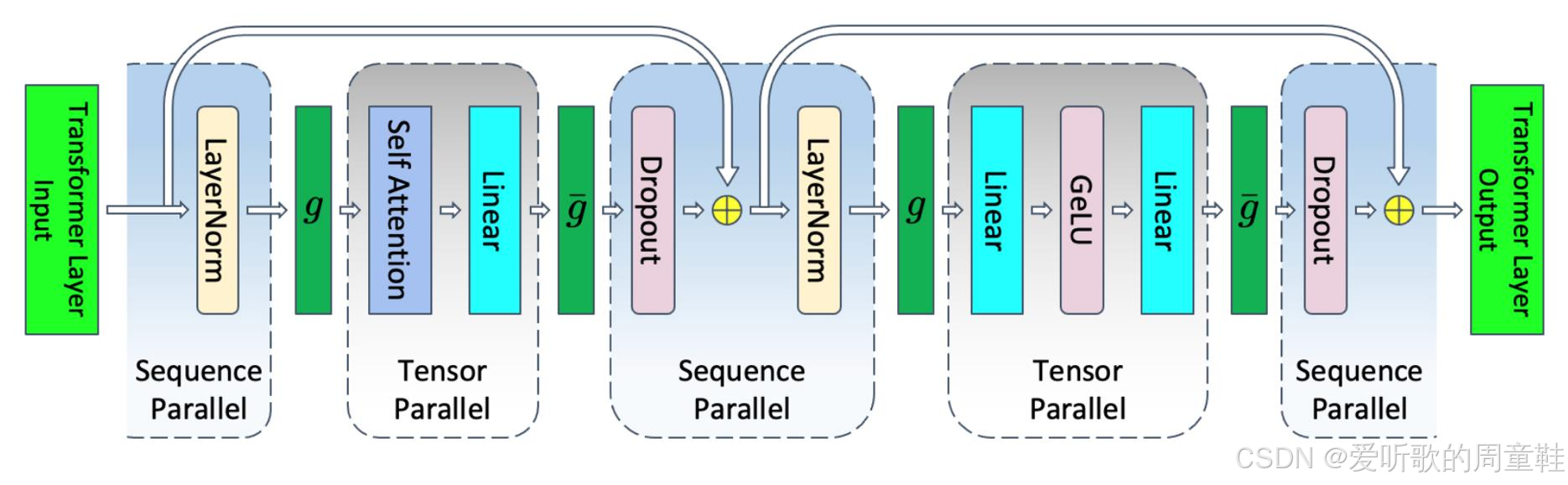
假设我们有一个长度为 1024 的序列，我们将序列切分后，每个设备只需处理该层归一化或 dropout 的不同片段，这些逐点运算现在可以完全按照序列维度进行拆分，由于现在我们要沿着序列维度进行切分，因此需要进行同步操作，以确保并行计算的结果能够正确聚合

在前向传播过程中，这些操作将采用全聚集（all gather），而梯度反向传播时则使用归约分散（reduce scatter），在反向传播时，这两种操作正好对调，从某种意义上说，这两种操作形成了完美的对偶关系，我们当前对层归一化的处理方式，本质上采用了数据分散的策略，因此我们需要将这些分散的数据重新聚合起来，才能执行标准的计算流程

接下来当执行到 dropout 层时，我们又需要将这些数据重新分散到并行计算组件中去，而在反向传播过程中，我们则以相反的顺序执行这些操作，希望这样的解释足够清晰明了

这个思路其实非常简单，我们只是将之前未能实现并行的最后几个组件进行了并行化处理，至此，我们终于可以将所有这些分散的模块整合起来，从最初完全不采用并行计算的起点出发，最终实现了完整的并行化方案。

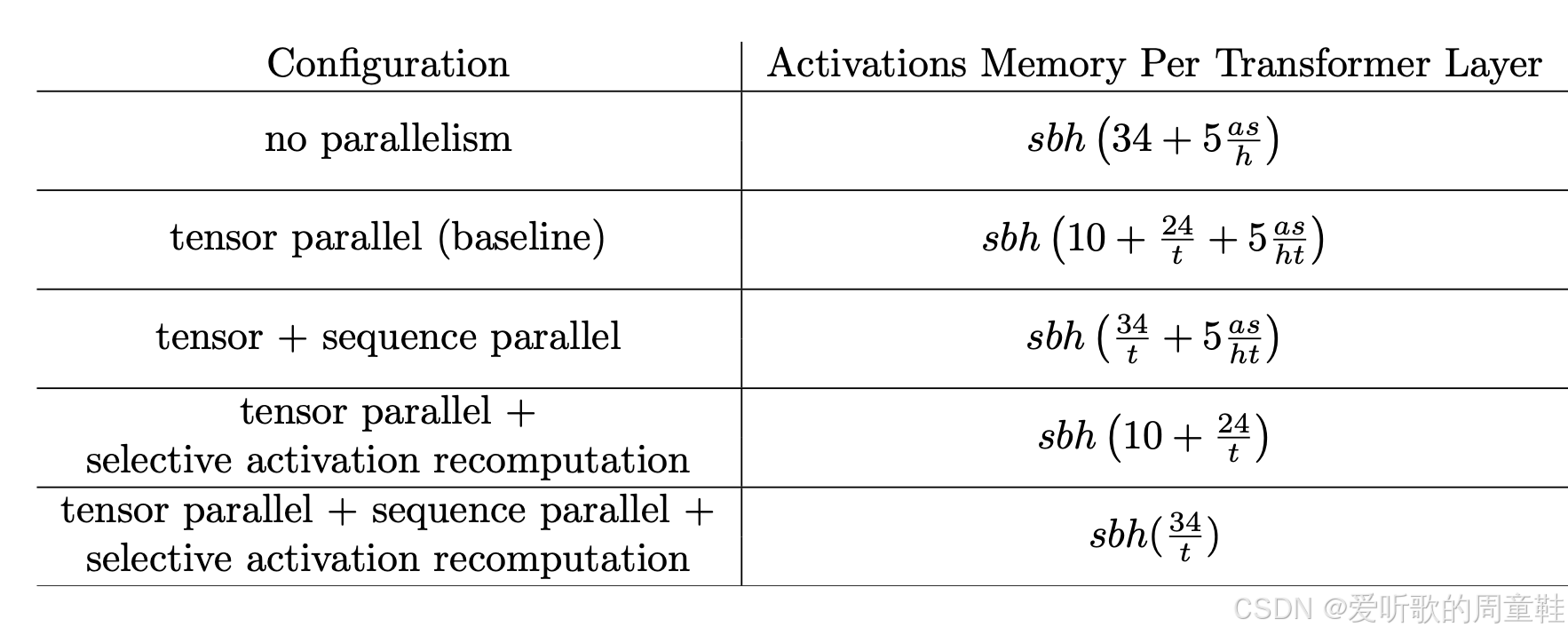
我们实现了张量并行（tensor parallelism），这使得所有非点对点运算都能被分割为 t 份并行处理，若再结合序列并行（sequence parallelism）技术，我们还能将这个组件的计算量进一步拆分为 t 份处理，我们还可以采用激活值重计算技术，这正是 Flash Attention 的精妙之处，通过这种方式彻底消除第二项的计算开销，而实际可达成的最低内存占用量正是 $sbh(\frac{34}{t})$ 这个底部的表达式

这种方案在实践中被广泛采用，在比较不同 Transformer 架构的内存计算公式时，我们最常关注的核心问题是：激活内存究竟占用了多少？常见的内存计算公式往往呈现出 $sbh\times 34$ 的基本形式，若采用 t 路张量并行，则只需除以 t，这正是此类内存优化方案中最容易实现的理论下限值

3.4 Other parallelism strategies

关于并行计算的其他策略我们就不展开讨论了，毕竟刚才已经带大家深入探讨了不少并行化的底层实现细节，这里我们快速过下

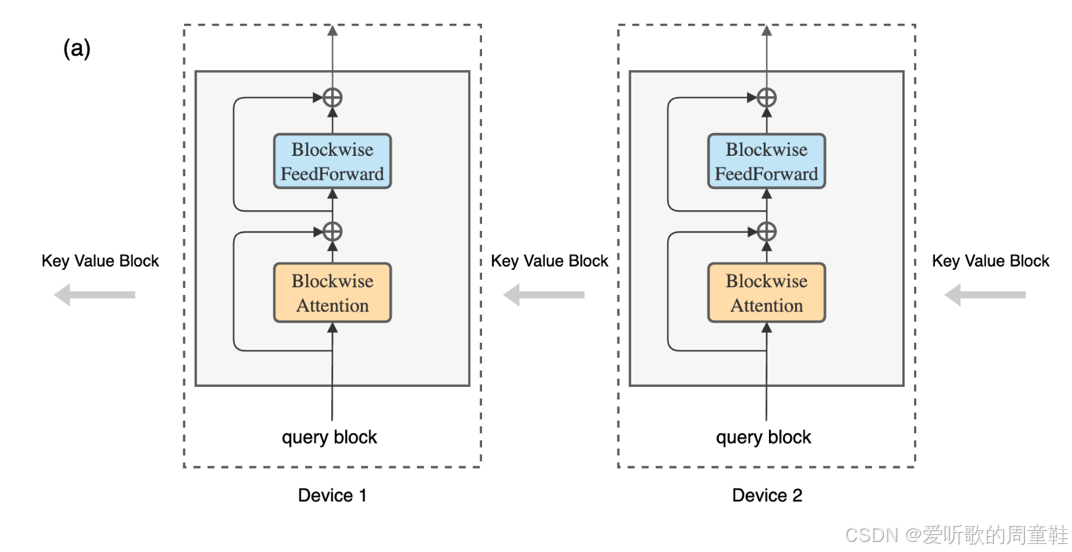
首先要讨论的是上下文并行（context parallel），也就是环形注意力机制（ring attention），大家可能听说过 “环形注意力” 这个概念，这种方法的核心在于将计算任务和激活值存储的开销进行双重拆分，在处理超大规模注意力机制时，其核心思路是通过在多台机器之间传递键值对（keys and values）来实现分布式计算

每台机器负责处理不同的查询（query），而键值对（keys and values）会以环形方式在机器间流转，就像接力赛跑那样，最终完成所有 QKV 内积的计算，这里最妙的是，大家其实已经掌握这个技术了，因为之前在实现 Flash Attention 时就用过类似的区块化（tiling）方法，大家已经知道注意力机制可以通过这种逐块（tile by tile）的在线计算方式来实现，这正是环形注意力（ring attention）机制的工作原理

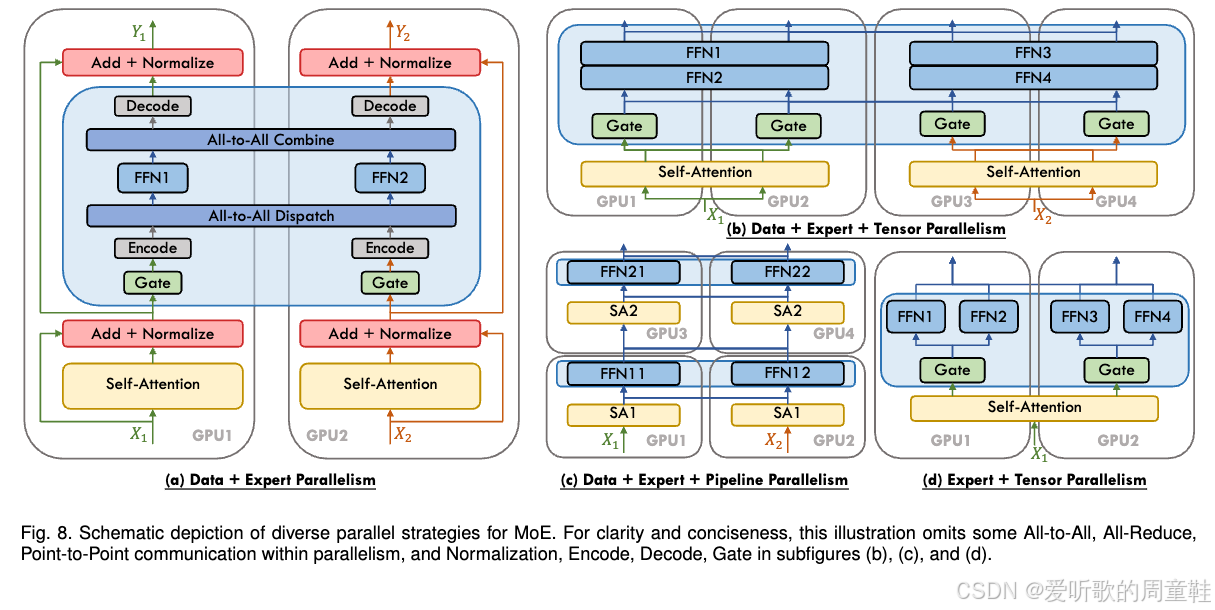
既然大家已经掌握了张量并行（tensor parallelism），那么理解专家并行（expert parallelism）就很简单了，专家并行可以理解为张量并行的变体，都是将大型多层感知机（MLP）拆分成若干专家子网络（expert MLPs），然后把这些子网络分布到不同的计算设备上运行

专家并行的核心区别在于：专家网络是稀疏激活的，因此需要特别设计路由机制（routing），与张量并行中可预测的全连接通信不同，这里的路由机制具有不确定性，比如某个专家模块可能突然出现过载情况，此时网络通信的复杂度会显著提升，但除此之外，专家并行在概念框架上与张量并行仍属于同一体系

3.5 Recap: LLM parallelism table…

让我们简单回顾一下讨论过的内容，这里整理了一个小表格，列出了我们现有的各类并行计算策略

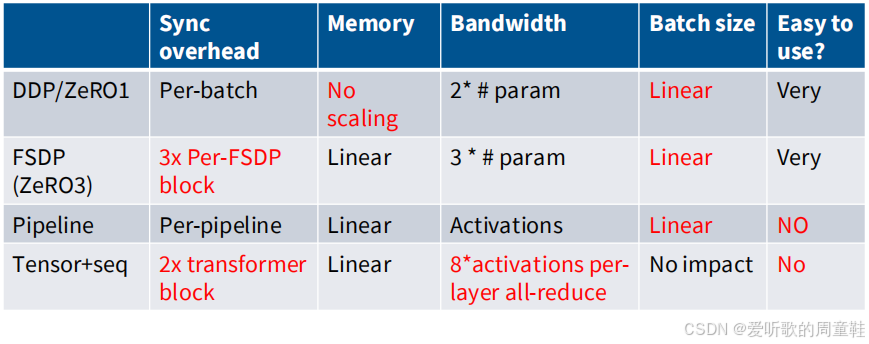
我们采用 ZeRO 1 中的 DDP（分布式数据并行）策略，这就是最基础的数据并行方案，这种方案存在每批次处理的开销，无法实现内存扩展，虽然带宽利用率尚可，但需要消耗更大的批量规模才能实施

数据并行化的规模取决于批量大小，批量越大，并行化程度才能越高，FSDP（全分片数据并行）可视为 ZeRO 1 的优化版本，它能实现内存扩展，但代价是需要承担跨神经网络层的额外计算开销，如此一来，不仅通信成本大幅增加，同步屏障还可能导致计算资源利用率低下

流水线并行的优势在于摆脱了批次处理的限制，同时能实现线性的内存扩展，但这种方法也存在明显缺陷，它不仅会占用宝贵的批量处理容量，而且配置和使用过程极其繁琐，因此只要条件允许，多数开发者都会尽量避免采用流水线并行方案

最后，张量并行对带宽要求极高，且需要频繁的同步操作，成本代价最为昂贵，但这种方案有个显著优势，那就是完全不会影响批量处理的规模，因此这种并行策略颇具价值，它能在不影响全局批次规模的前提下实现并行计算，这一优势相当难得

因此我们必须在多种有限资源之间寻求平衡，内存便是其中一项关键资源，带宽与算力构成了另一种核心资源，而批量大小则属于非常规资源，尽管它看似抽象，但实际使用时必须将其视为有限资源进行调配，通过在不同环节的合理分配来提升整体效率

4. Part 3: Scaling and training big LMs with parallelism

谷歌前段时间发布了一份非常出色的 TPU 并行计算指南，我们不妨称之为 TPU book，值得一提的是，这份指南中关于并行计算的章节确实写得非常精彩，在进入具体案例之前，我们先给大家展示这份指南中一个非常出色的示意图

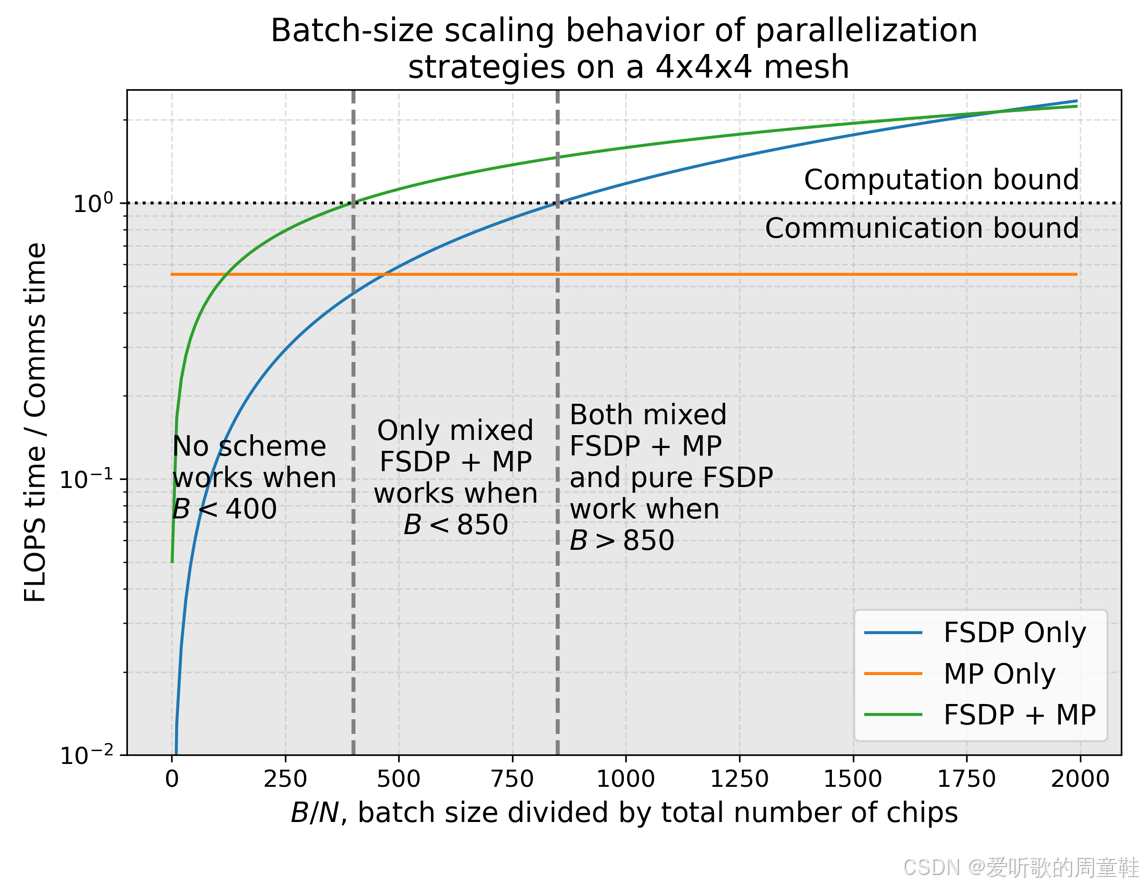
正如我们之前强调的，批量大小才是关键参数，根据批量大小与 GPU 数量之比的不同，最优的并行策略也会相应变化，因此他们采用特定公式来计算每个模型最终所需的通信量与计算量

这个简化公式用于生成上面的图表，显然，当批量过小而 GPU 数量过多时，系统效率必然低下，此时系统始终受限于通信瓶颈，图表下半区正是这种情形，实际上，大部分时间都消耗在通信环节上，随着批量规模的逐步增大，最终当结合使用 FSDP（即 ZeRO 第三阶段）与张量并行时，系统将突破瓶颈，达到计算资源满载的理想状态

此时浮点运算资源得以充分利用，不再因等待通信而闲置，最终当批量规模足够大时，仅需采用纯数据并行即可实现高效训练，采用纯 FSDP 方案时，计算耗时终将超越通信耗时，实现训练效率的质变突破，因此只要批量规模足够大，仅用 FSDP 就能实现高效训练

这个示例生动诠释了混合并行策略的精妙之处：何时需要组合使用不同策略以及批量规模为何成为关键资源要素。通过这种直观的演示方式，相信你已经对这些概念有了清晰的认识

当这些技术有机结合时，就形成了业界所称的 3D 或 4D 并行方案，最近似乎还出现了 5D 并行这样的新术语，目前第五个维度的具体含义尚不明确，但现在你已经能够将这些不同维度的并行技术融会贯通了

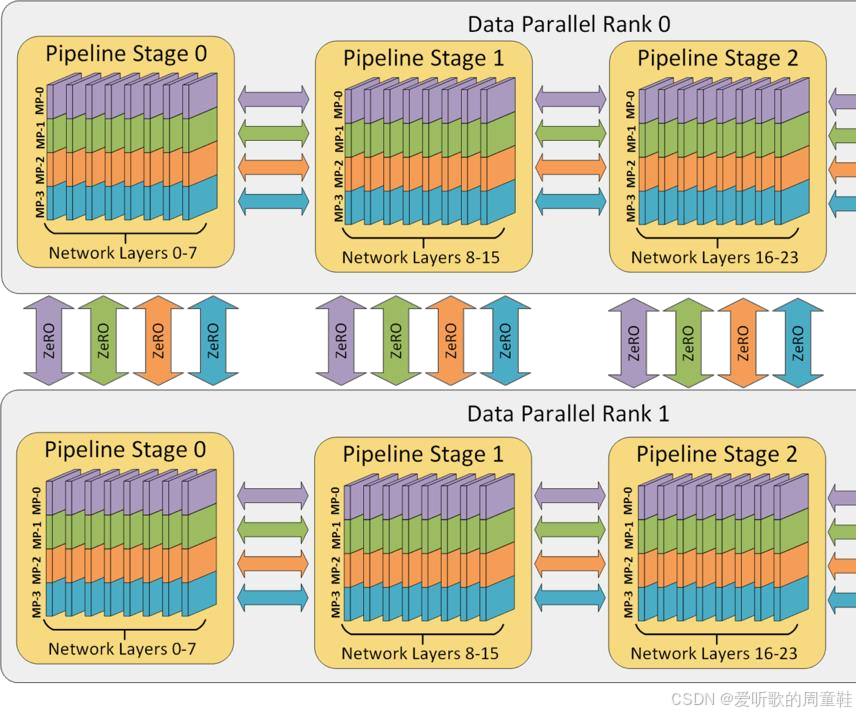
这里有个非常实用的经验法则，首先必须确保模型参数和激活值都能装入内存，如果连这一步都做不到，训练就无从谈起，这是最基本的前提条件，因此在模型完全载入内存之前，我们必须对模型进行拆分，因此我们需要采用张量并行方案

众所周知，在单台机器的 GPU 数量范围内，这种并行方式效率极高，因此我们将在这个范围内实施张量并行。接下来，根据你对流水线并行的需求或带宽限制等实际情况，你需要在跨机器部署时选择使用 ZeRO 3 或流水线并行方案，直至模型能够完整载入内存

当突破这个临界点后（直至耗尽所有 GPU 资源），你就能完整运行整个模型，此时唯一目标就是最大化可用的算力规模，因此剩余阶段将采用数据并行进行扩展。这种方案在低带宽通信环境下表现优异，且实现方式极为简洁，这样就能充分利用所有 GPU 资源，若批处理规模过小，可采用批处理规模与通信效率的置换策略，当批处理规模资源尚未耗尽时，可在设备端采用梯度累积技术，这样即便受限于内存容量，也能实现等效的大批次训练效果

该方案实现了批处理规模与通信效率的优化置换，通过降低跨机器同步频率，基本原则很简单，无论进行何种训练，这种方法都能保证模型获得理想的训练效率，为了让这个概念更具体，我们将在最后通过几个实例来说明

我们将快速展示 2021 年 Narayanan 大语言模型那篇精彩的论文 [Narayanan+ 2021]，它用图示直观展示程序了这些原理，并包含大量消融实验，同时也会涉及去年发布的部分模型案例

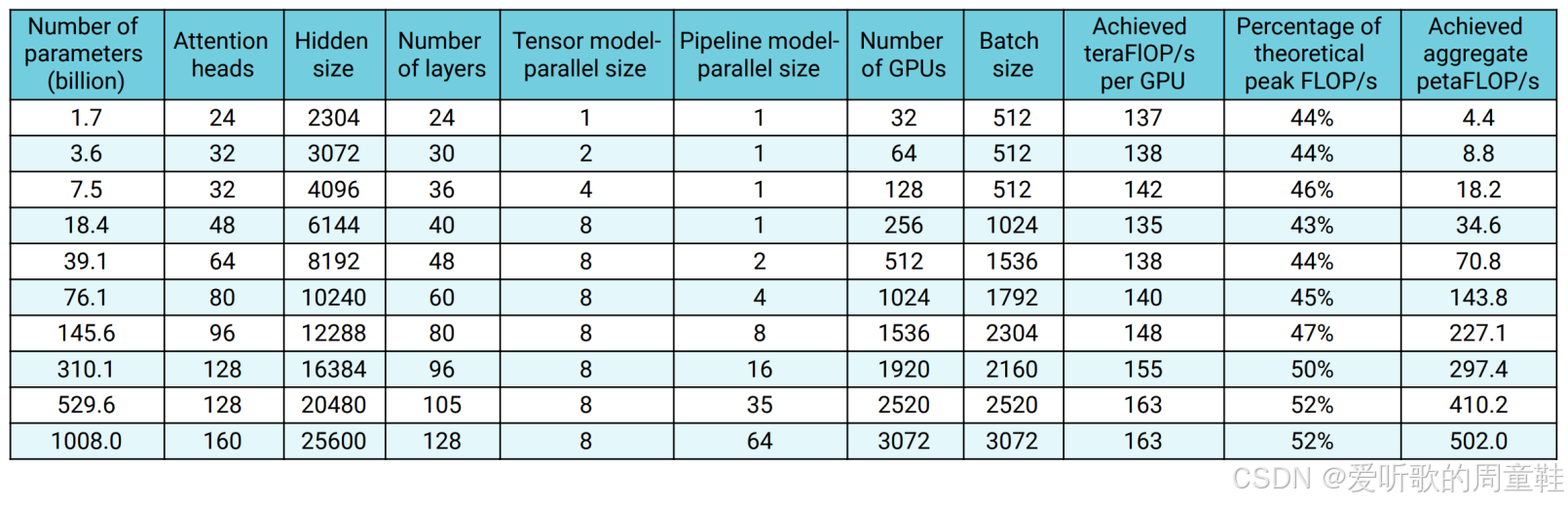
上面这张表格详细记录了他们的模型训练规模，从 17 亿参数到 1 万亿参数的完整演进过程，所有规模的模型都实现了极高的计算资源利用率，从表格中可以看出，他们实现的浮点运算效率达到了理论峰值的 40% 至 52%，这个数值相当出色

从表格可见，张量并行度初始值为 1，最终逐步提升至 8 后达到上限，因此他们首先采用了张量并行策略，而流水线并行度则始终保持为 1。但随着模型规模增长到一定程度时，这些大型模型就无法完整装载了，因此必须提升流水线并行度来进行补偿

数据并行规模最初会尽可能设到最大，随后逐渐减小，因为随着流水线并行度的提升，这部分资源实际上会挤占批处理规模的可用空间。因此，从某种意义上说，如果这些资源被用于流水线并行，你就无法真正实现那么大的批量规模了

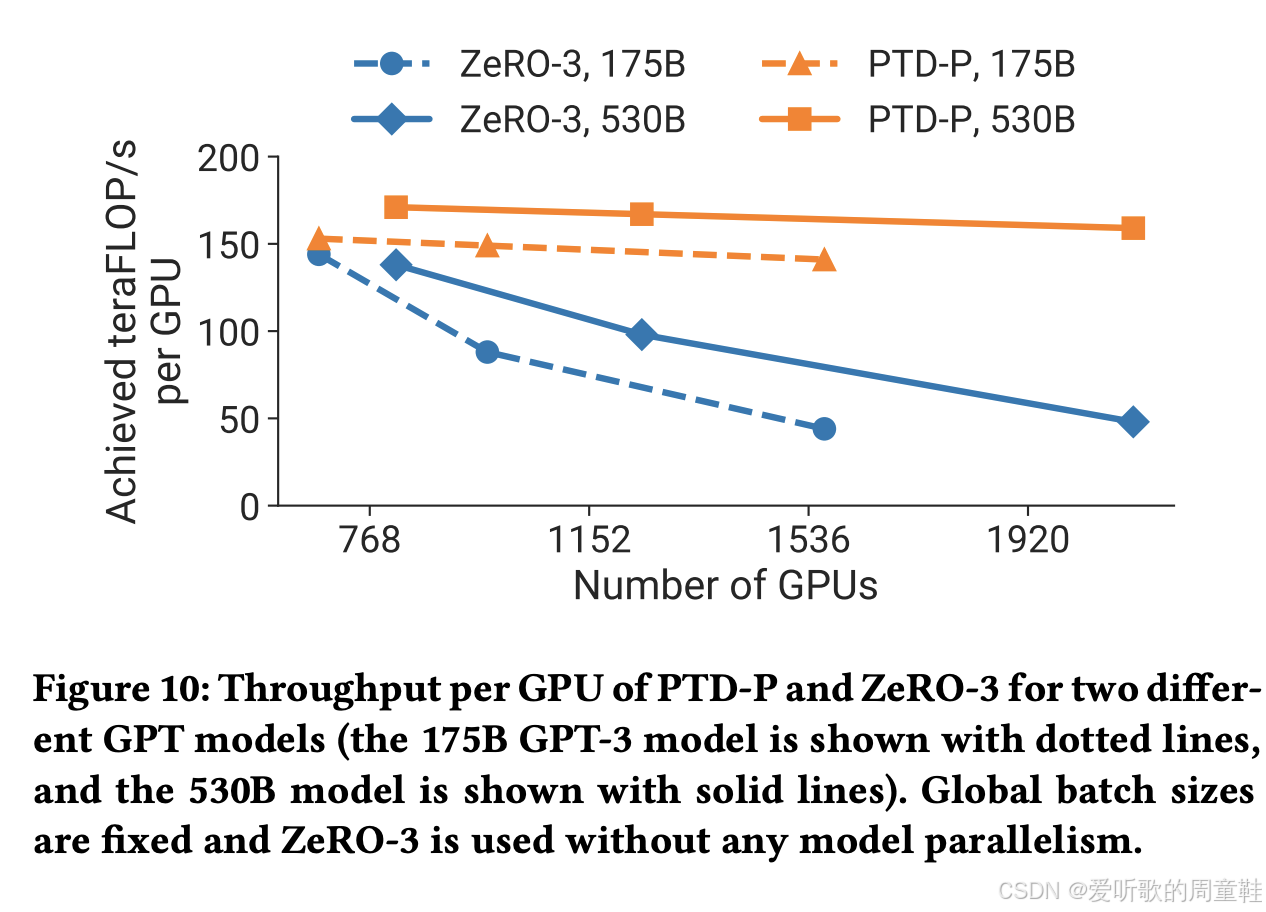
因此，精心设计的 3D 并行策略将带来聚合计算能力的线性提升，由此可见，通过精心设计的 3D 并行方案，每块 GPU 的实际算力利用率能保持近乎水平线般的稳定表现，这意味着当你增加 GPU 数量时，系统总吞吐量将实现完美的线性扩展，这确实非常理想

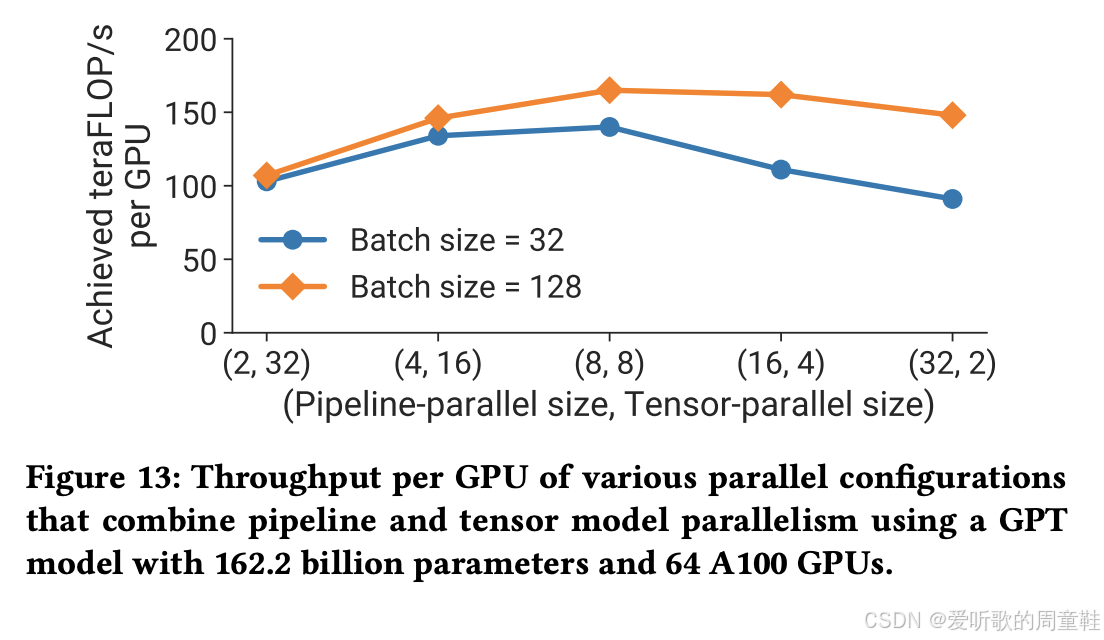
张量并行度设为 8 通常是最优选择，上图展示的是流水线并行规模与张量并行规模，可用看到，当并行度设为 (8,8) 且批次大小为 128 时，系统将达到最优性能，即便采用较小的批次规模，张量并行度保持为 8 仍是最优解

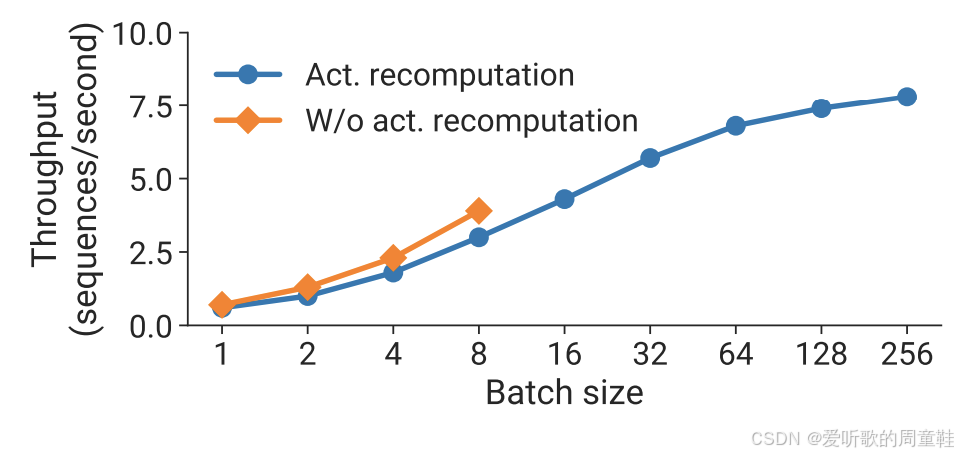
而激活重计算技术则能支持更大的批次规模，需要注意的是，更大的批次规模反过来有助于掩盖流水线并行带来的额外开销，因此，尽管激活重计算会增加浮点运算量，但其带来的收益足以抵消额外开销，这个现象在 Flash Attention 技术中已经得到验证

下面我们快速看下业界主流的并行化策略实检方案

OLMo 与 Dolma 论文显示，针对 70 亿参数模型采用了全分片数据并行（FSDP）方案

DeepSeek 的首篇论文采用了零冗余优化器第一阶段（ZeRO 1）结合张量序列与流水线并行的方案，这正是我们之前提到的标准实现方案。V3 版本实际采用了略有差异的实施方案，该方案采用 16 路流水线并行、64 路专家并行（本质属于张量并行变体），并搭配零冗余优化器第一阶段（ZeRO 1）实现数据并行策略

另一国产模型 Yi 同样采用了零冗余优化器第一阶段（ZeRO 1）结合张量与流水线并行的方案，而 Yi-lightning 版本因采用混合专家架构，将原有的张量并行替换为专家并行方案

若你对前言分布式训练技术细节感兴趣，Llama3 的技术报告非常值得研读，该报告阐述了网络架构与具体实施细节。正如文中所述，这些方案再次印证了我们先前提到的技术路线，这里采用了张量并行度为 8 的配置，同时运用了上下文并行（CP）策略，该策略仅适用于长上下文训练场景，即整个训练流程的最终阶段，因此这部分可以暂时忽略

在前两个训练阶段中，同时采用了流水线并行与数据并行策略，实际上第一阶段也可忽略，这只是他们为确保训练稳定性而采用的小批量预训练环节。若分析其并行策略的设计逻辑，可发现：正如前文所述，其并行策略的优先级排序完全遵循带宽需求原则，首先采用张量并行（TP）与通信并行（CP），其次流水线并行，最后才是数据并行（DP）

数据并行之所以能置于末尾，正是因为它对网络延迟具有强容忍性，通过异步获取分片模型权重即可实现高校训练，因此，他们正是采用了我们所阐述的这种策略来训练超大规模模型

关于 Llama3 有个趣闻，或许你已从朋友间的闲聊中听闻，当进行超大规模模型训练时，GPU 故障会频繁发生，故障 GPU 导致了 148 次训练中断，占其总中断次数的 30%，他们还遭遇了诸如机器突发维护等意外状况，这类突发状态共计 32 起，导致训练过程中断了 32 次

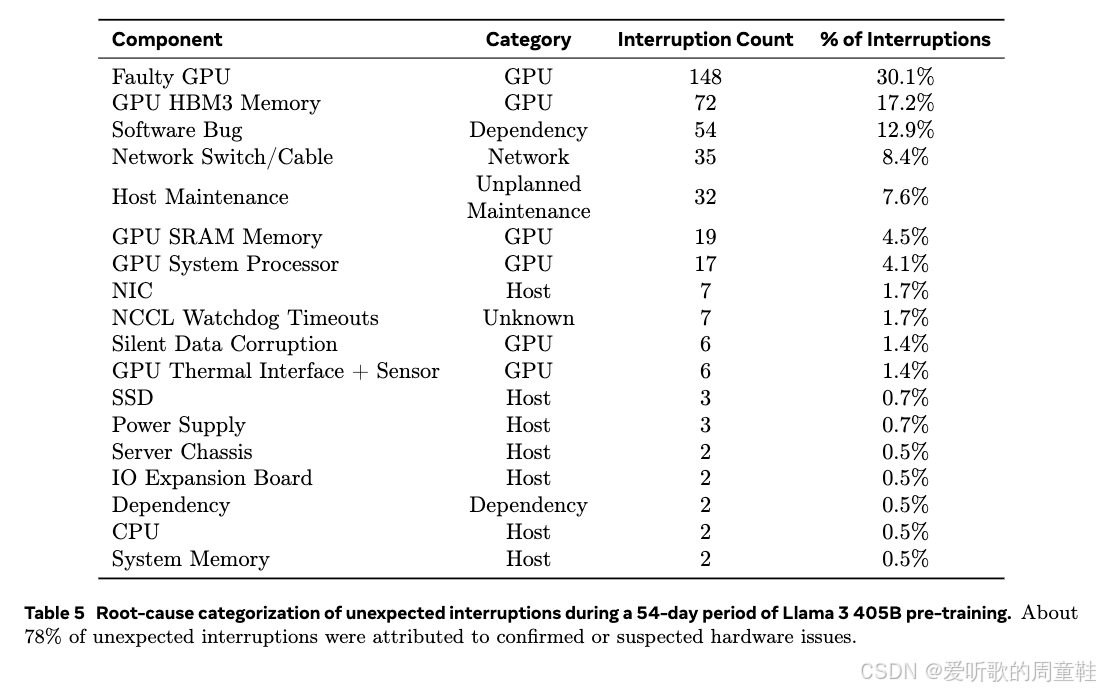
因此，当你训练如此庞大的模型时，虽然我们讨论了算法层面，但实际还需要构建具备容错能力的系统架构，才能有效应对这类突发状况

最后一个案例来自于 Gemma 2项目，我们用这个案例来收尾，因为它恰是一个 TPU 集群的典型范例，他们采用的是零冗余优化器第三阶段（ZeRO 3），器原理基本等同于完全分片数据并行（FSDP），同时结合了模型并行与数据并行策略，正如我们前面提到的，TPU 的架构特性让他们能够将模型并行策略的潜力发挥得更充分

5. Recap for the whole lecture

综上所述，要实现超越某个临界点的扩展，必须采用跨多 GPU、跨节点的并行计算架构，不存在放之四海而皆准的单一方案，因此需要融合这三种方法，优势互补，而在实际应用中，还存在着一些简单直观的经验法则来指导并行策略的实施。

OK，以上就是本次讲座的全部内容了

结语

本讲我们主要讲解了大语言模型在多 GPU 与多机器环境下的 并行化训练策略，涵盖网络通信原理、数据与模型并行的实现机制、激活内存优化以及多种并行方案的性能权衡。
在 并行化动机 小节中，我们首先指出单块 GPU 已无法同时满足算力与显存需求，因此必须通过跨设备协同来实现计算与内存的线性扩展。课程首先回顾了 GPU 集群的典型互联架构（NVLink、InfiniBand），并介绍了集合通信原语如 all-reduce、reduce-scatter、all-gather 的等价关系，说明分布式训练性能的关键本质上取决于这些通信操作的次数与带宽利用率。

在 数据并行（Data Parallelism） 小节，我们从最基础的随机梯度下降（SGD）出发，介绍了分布式批次拆分与梯度同步机制。随后系统讲解了 ZeRO 系列优化技术：Stage 1（优化器状态分片）通过在不同 GPU 上分配一阶、二阶矩状态，将显存占用从百 GB 级降至几十 GB；Stage 2（梯度分片）进一步在反向传播阶段逐层归约梯度并即时释放，从而保持显存常数上限；Stage 3 / FSDP（全分片数据并行）在计算图前后向过程中按需聚合参数，实现“边通信边计算”的流式调度，使计算与通信几乎完全重叠。这一系列设计使得参数、梯度与优化器状态的内存消耗均能随 GPU 数量线性缩减，从而支撑百亿参数级模型的训练。

在 模型并行（Model Parallelism） 小节，课程介绍了两种核心形式：流水线并行和张量并行。流水线并行（Pipeline Parallelism） 沿网络深度划分模型，让不同 GPU 负责不同层级；通过微批次（micro-batch）填充流水线减少“气泡”时间，并可利用 1F1B（前向-反向交错）或 Dual-Pipe 机制进一步实现零空泡执行。张量并行（Tensor Parallelism） 则沿矩阵宽度拆分大型算子，在前向与反向传播中使用两次 all-reduce 完成子结果汇总。该方法实现简单、无批量依赖，是当前主流的多 GPU 并行方式，但对互联带宽要求极高，通常仅在单机 8 GPU 内使用。

在 激活并行（Activation Parallelism） 小节中，我们看到显存瓶颈往往来自激活值。课程展示了 NVIDIA 的研究结果并推导出 Transformer 单层的激活内存公式，说明仅依靠张量或流水线并行仍存在不可并行的残余项。为此，引入 序列并行（Sequence Parallelism），沿序列维度划分逐点运算（如 LayerNorm、Dropout），并在前向与反向过程中分别使用 all-gather 与 reduce-scatter 维持正确性，从而进一步降低激活占用。

最后我们将前面讲解的各类并行方法综合起来，展示了当今主流大模型（如 GPT-3、PaLM、LLaMA 等）在真实训练中的 系统级并行化架构。进一步强调：想要让数百亿乃至上万亿参数的模型成功训练，必须在多维度上同时实现可扩展性—包括 计算扩展、显存扩展、通信扩展与训练稳定性。

整个讲解非常通俗易懂，大家感兴趣的可以看看

下节课我们将进一步探讨跨多块 GPU 的并行化方案，敬请期待🤗

参考

• https://stanford-cs336.github.io/spring2025
• https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_
• https://github.com/stanford-cs336/spring2025-lectures
• https://github.com/stanford-cs336/spring2025-lectures/tree/main/nonexecutable/7-Parallelism basics.pdf