QC-LDPC码的表示

        QC-LDPC码作为一种结构化的LDPC码，可以通过代数构造得到。QC-LDPC 码的校验矩阵由不同偏移量的循环移位子矩阵和零矩阵构成。

校验矩阵所具有的准循环的特性使得在编译码硬件实现过程中复杂度低，便于在大规模集成电路上实现。

        QC-LDPC码在设计时需要先构造一个大小为 维的稀疏矩阵作为基矩阵或称之为基图（Basic graph，BG），然后将这个基矩阵扩充Z 倍，Z 被称之为扩展因子，扩充之后校验矩阵的维度变成。
因QC-LDPC码具有的良好结构特性，已经被应用到众多通信标准中，如5G、IEEE 802.11n、WiMax、WLAN 等标准。

相比于其它类型的LDPC 码，QC-LDPC 码具有如下几个优点：
（1）基矩阵的维度一般比较小，可以直观看到矩阵的全貌，进而大致了解校验矩阵的性能；
（2）容易对矩阵进行描述。当LDPC的码长较长时，对应的校验矩阵规模是比较大的，难以对其进行描述。而QC-LDPC码在描述时，只需要在基矩阵的对应位置用移位值表示即可；
（3）硬件实现复杂度低。在编译码过程中，容易实现以扩展因子Z为大小的并行度。

        由于H矩阵的维度过大，一般难以通过直接表示校验矩阵来获得校验矩阵的全貌信息。在QC-LDPC 码中，一般用基矩阵通过扩展得到校验矩阵H。基矩阵又称之为置换移位矩阵，一个大小为的基矩阵如下式所示。

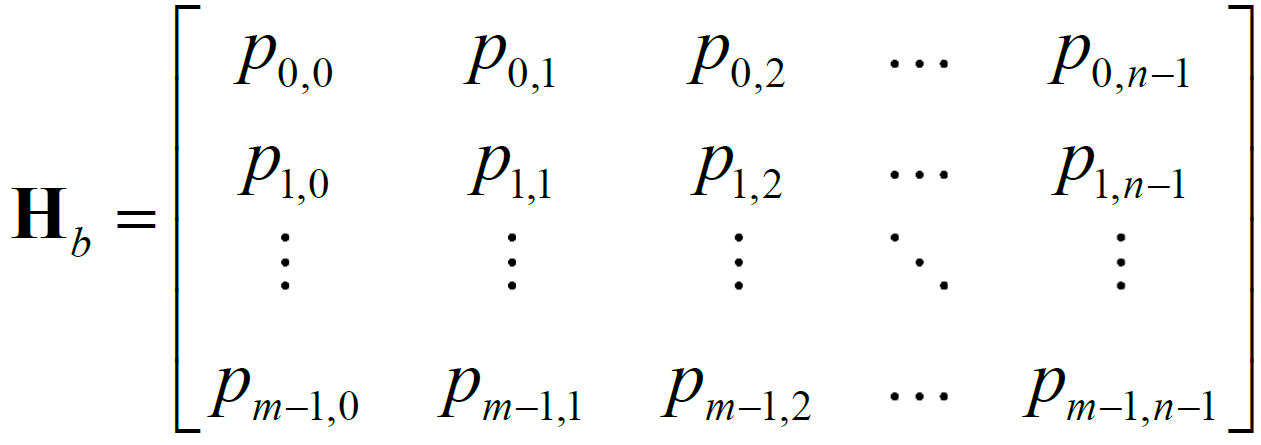
        置换移位矩阵的移位值表示中对应的第（i，j）个元素。移位值对应的循环移位子矩阵向右循环移位次，其中。已知置换移位矩阵和扩展因子Z，可以按照如下规则将基矩阵恢复为完整的校验矩阵H。
（1）当=-1时，移位值被替换为的全 0 矩阵；
（2）当=k时，移位值被替换为的单位矩阵向右循环移位 k位后得到的矩阵。特别的，如果移位值为0 则将会被替换为的单位矩阵。
以扩展因子为Z =4 为例，下图给出了不同移位值下对应的移位矩阵：

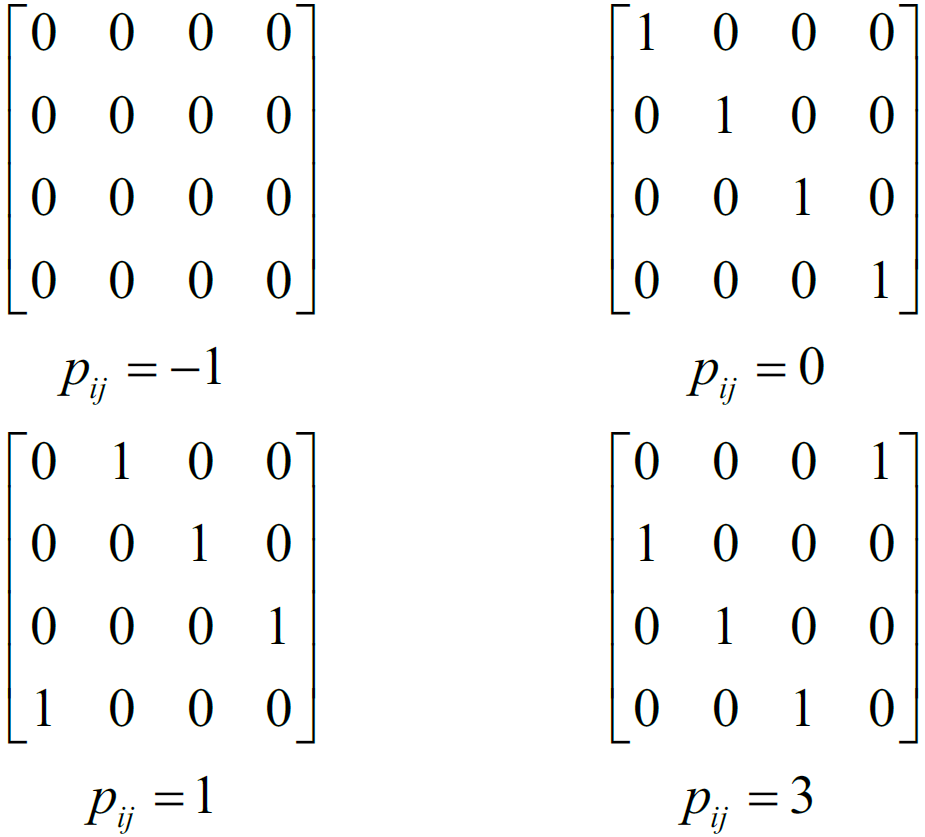
        校验矩阵H与基矩阵之间的大小关系为：。其中校验矩阵H 的行数为m，列数为n。基矩阵的行数为，列数为。