算法--二分查找
算法原理
1.二分算法的特点:与其他算法相比,在未了解本质的情况下是最恶心、细节最多、最容易写出死循环的算法,但当我们了解了二分算法的本质后,他将变得十分轻松
2.学习的侧重点
1.算法原理(***很重要)
2.模版
1.朴素的二分模版 十分简单,我们之前就有接触过,有限制
2.查找左边界的二分模版 2,3细节多,适用范围广
3.查找右边界的二分模版
题目解析
1.二分查找
https://leetcode.cn/problems/binary-search/description/
题目解析
给定一个有序的nums和一个目标值t,在数组中搜索t,找到返回数组下标,找不到,返回-1
算法原理
解法一:暴力解法O(N)
for循环遍历
解法二:二分查找
数组是有序的,我们可以利用二段性来解决这一问题
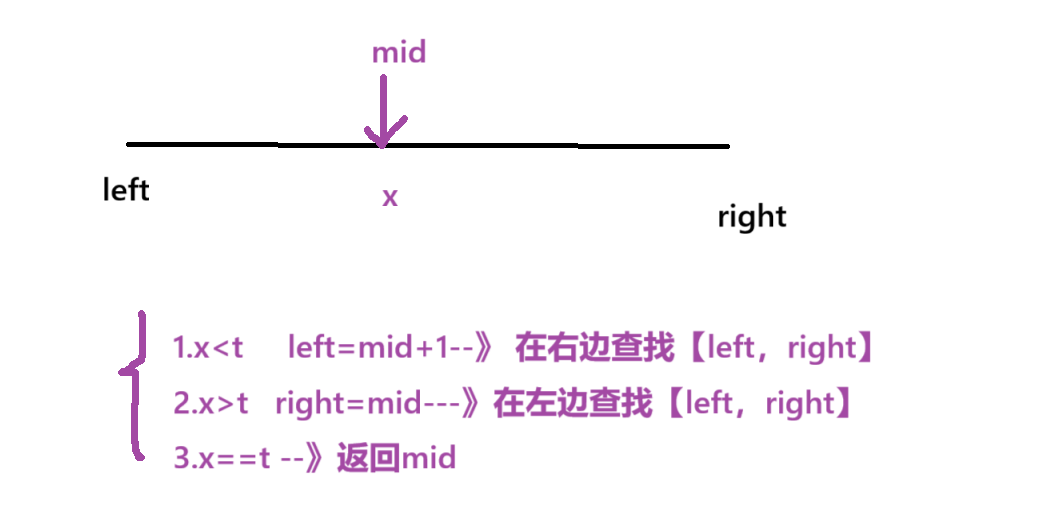
总结朴素二分模版

防溢出的操作
left+(right-left+1)/2
代码实现
class Solution {public int search(int[] nums, int target) {int left=0,right=nums.length-1;while(left<right){int mid=left+(right-left)/2;if(target<nums[mid]){right=mid-1;}else if(target>nums[mid]){left=mid+1;}else{return mid;}}return -1;}
}2.在排序数组中查找元素的第一个和最后一个位置
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/
题目解析
给定一个递增的数组nums,和一个目标值,找到给定目标在数组开始位置和结束位置
如果不存在,则返回[-1,-1]
算法原理
解法一:暴力解法
解法二:二分解法
利用二段性
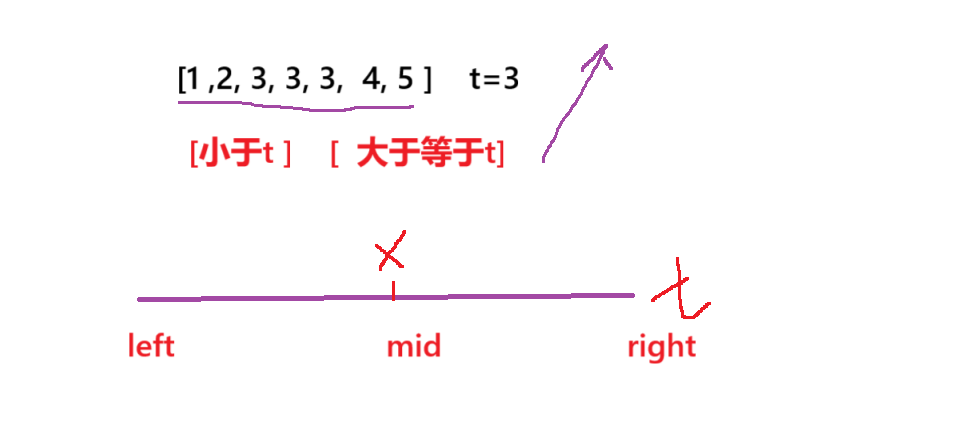

总结朴素的二分模版
while(left<right){
int mid=left+(right-left)/2;
if(...){
left=mid+1;
}else if(..){
right=mid-1;
}else{
return
}
}
注意 要具体分析,不要一味的套用模版
代码实现
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret=new int[2];ret[0]=ret[1]=-1;//处理边界情况if(nums.length==0) return ret;//1.先二分左端点int left=0,right=nums.length-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target){left=mid+1;}else{right=mid;}}//判断是否有结果if(nums[left]!=target){return ret;}else{ret[0]=left;}//2二分右端点right=nums.length-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]>target){right=mid-1;}else{left=mid;}}if(nums[right]!=target){return ret;}else{ret[1]=right;}return ret;}
}3.x的平方根
https://leetcode.cn/problems/sqrtx/description/
题目解析
给定一个非负整数,计算并返回x的最小平方根
不允许使用任何的内置函数和算符
算法原理
解法一:暴力解法

解法二:二分查找
利用二段性,使用二分查找
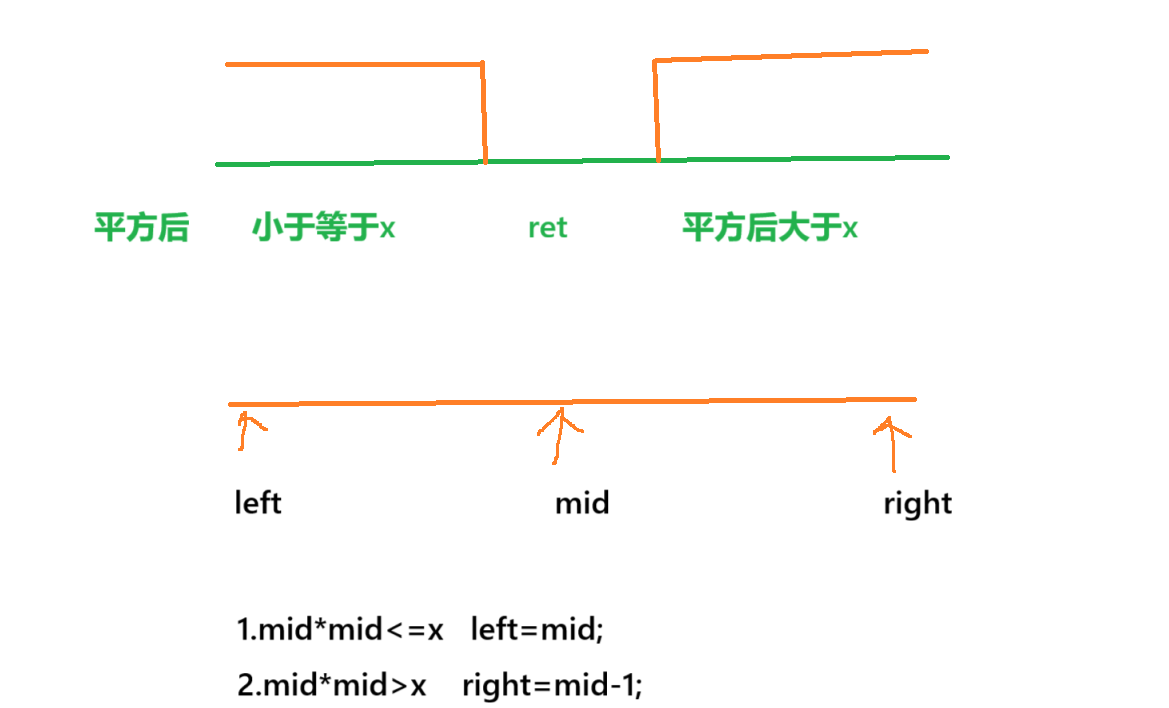
代码实现
class Solution {public int mySqrt(int x) {if(x<1) return 0;long left=1,right=x;while(left<right){long mid=left+(right-left+1)/2;if(mid*mid<=x){left=mid;}else{right=mid-1;}}return (int)left;}
}4.搜索插入的位置
https://leetcode.cn/problems/search-insert-position/description/
题目解析
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引,如果目标值不存在于数组中,返回他将会被按顺序插入的位置
算法原理
解法一:暴力遍历
解法二:二分法
分析其二段性
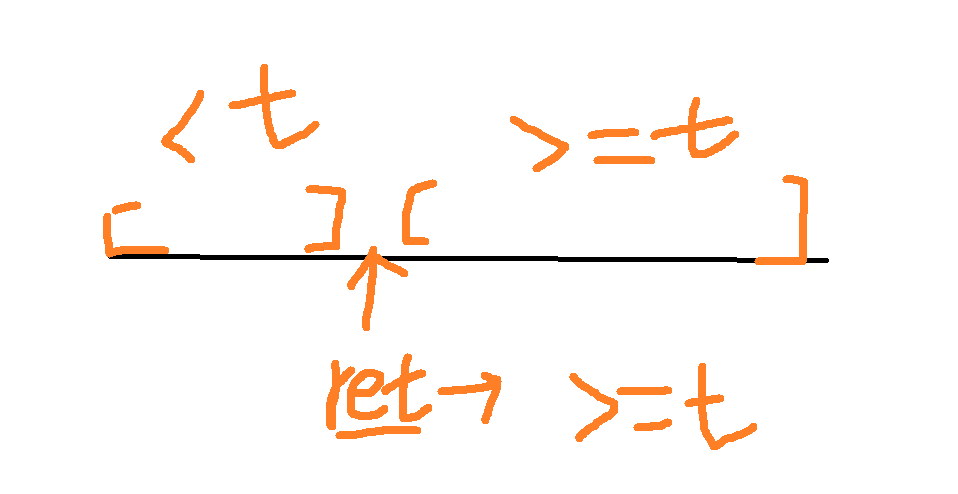
注意在返回结果之前比较一下返回值和目标值的大小
代码实现
class Solution {public int searchInsert(int[] nums, int target) {int left=0,right=nums.length-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target){left=mid+1;}else {right=mid;}}if(nums[left]<target){return left+1;}return left;}
}