基于张祥前统一场论的太空中引力确定方法研究
基于张祥前统一场论的太空中引力确定方法研究
摘要
本文在张祥前统一场论框架下,探讨该理论对引力本质的独特定义,并推导基于此定义的太空中引力确定方法。在该理论体系下,引力被描述为"物体周围空间向物体的加速运动",与传统认知存在显著差异;太空中确定引力的核心逻辑是通过观测自由测试质点的相对运动,反推局部空间的加速状态,进而获取引力场参数。该方法提供了一种以空间为对象的引力测量路径,具有直观的动力学特征。
1 引言
传统引力研究中,太空引力确定多依赖大质量天体作为参考系,或通过观测时空几何效应间接推断,存在参考系局限或测量复杂的问题。张祥前统一场论提出了不同视角,从"空间运动"角度重新诠释引力本质,为太空中引力的直接测量提供了新的理论构想。本文旨在梳理该理论框架下引力的核心逻辑,并探讨其太空测量方法与理论依据。
2 理论基础:张祥前统一场论中的引力本质
该理论对引力的定义构成了太空测量方法的核心前提,其核心观点可概括为:
-
引力的空间动力学解释
在该理论框架下,“引力场的本质被描述为物体周围空间本身向物体加速运动的加速度”。这一描述提供了与传统认知不同的视角 —— 物体所在的空间会持续向物体质心加速运动,这种空间运动状态被视为引力场的本质。例如,地球附近的空间被认为以"朝向地心"的方向加速流动。
-
“重量” 的力学起源
物体的"重量"被解释为物体静止在"加速流动的空间"中时,被支撑物(如地面、桌面)阻挡所产生的压力。当物体失去支撑(如自由落体),其运动状态与空间加速状态一致,表现出"失重"现象,即物体与空间运动同步,无相对加速度。
3 太空中引力确定的操作方法与逻辑推导
基于 “引力是空间加速运动” 的核心理论,该方法通过 “观测自由质点的相对运动” 反推空间状态,进而确定引力,具体步骤如下:
3.1 准备:释放理想测试质点
在飞船或观测点附近,释放一个 “理想测试质点”。该质点需满足两个条件:一是质量足够小,避免自身引力干扰局部空间状态;二是不受非引力作用(如电磁力、碰撞、大气阻力等),确保其运动完全由空间加速状态决定。
3.2 观测:分析质点的相对运动轨迹
通过观测质点相对于观测者(或飞船)的运动,可直接推断局部空间的引力场状态,分为两种核心场景:
-
场景 A:质点相对静止
若测试质点与观测者保持相对静止,说明观测者与质点所处的局部空间无相对加速运动。据此推断:此处引力场为零。
典型应用场景包括:远离任何大质量天体的星际空间(无明显引力源)、处于自由落体轨道的空间站(观测者与空间加速状态同步,局部空间表现为 “平坦”)。
-
场景 B:质点相对加速
若测试质点相对于观测者产生持续的加速运动,说明局部空间正在发生 “朝向引力源的加速流动”,质点的运动是空间加速的直接体现。据此推断:此处存在引力场,质点的加速度即反映空间加速状态。
3.3 计算:确定引力场的大小与方向
通过质点的相对加速数据,可直接获取引力场的关键参数:
-
方向:质点的加速方向与空间流动方向相反。例如,质点向观测者"左侧"加速,说明空间正"右侧"(即引力源所在方向)加速流动,因此引力场方向 = 空间流动方向 = 指向引力源。
-
大小:测试质点的相对加速度数值(记为aaa),与该点引力场强度(记为AAA)完全相等。
3.4 数学推导:引力场方程的理论基础
在张祥前统一场论框架下,引力场的数学定义方程可表示为:
A→=−GkΔnr→ΔSr\overrightarrow{A} = -\frac{G k \Delta n \overrightarrow{r}}{\Delta S r}A=−ΔSrGkΔnr
其中:
- GGG 是万有引力常数
- kkk 是比例常数
- Δn\Delta nΔn 是穿过面元的空间位移矢量条数
- ΔS\Delta SΔS 是高斯球面上的矢量面元面积
- r→\overrightarrow{r}r 是由质量中心指向空间点的位矢
- rrr 是位矢的标量长度
通过质量定义方程 m=kΔnΩm = \frac{k \Delta n}{\Omega}m=ΩkΔn(其中Ω\OmegaΩ是立体角),可将引力场方程转化为:
A→=−Gmr→r3\overrightarrow{A} = -\frac{G m \overrightarrow{r}}{r^3}A=−r3Gmr
这一方程具有以下数学性质:
-
旋度为零,表明引力场是保守场:
∇⃗×A⃗=0⃗\vec{\nabla} \times \vec{A} = \vec{0}∇×A=0 -
在远离质量点处(r≠0r \neq 0r=0),引力场散度为零:
∇⃗⋅A⃗=0\vec{\nabla} \cdot \vec{A} = 0∇⋅A=0 -
在质量点处(r→0r \rightarrow 0r→0),散度与质量密度成正比:
∇⃗⋅A⃗=−4πGu\vec{\nabla} \cdot \vec{A} = -4\pi G u∇⋅A=−4πGu
其中uuu是质量密度,定义为单位体积内的质量,即u=dmdVu = \frac{dm}{dV}u=dVdm。
3.5 质量密度uuu的详细推导过程
为完整证明上述结论,我们进行以下详细求导:
-
质量的几何化定义:
m=kΔnΩm = \frac{k \Delta n}{\Omega}m=ΩkΔn其中Ω\OmegaΩ是立体角,对于球对称情况,Ω=ΔSr2\Omega = \frac{\Delta S}{r^2}Ω=r2ΔS,代入得:
m=kΔnr2ΔSm = \frac{k \Delta n r^2}{\Delta S}m=ΔSkΔnr2 -
质量密度的定义:
u=limΔV→0ΔmΔVu = \lim_{\Delta V \to 0} \frac{\Delta m}{\Delta V}u=ΔV→0limΔVΔm其中ΔV\Delta VΔV是体积元。对于连续分布的质量,我们可以将质量表示为积分形式:
m=∫Vu dVm = \int_V u \, dVm=∫VudV -
引力场散度的计算:
球对称引力场的矢量分布与高斯定理应用
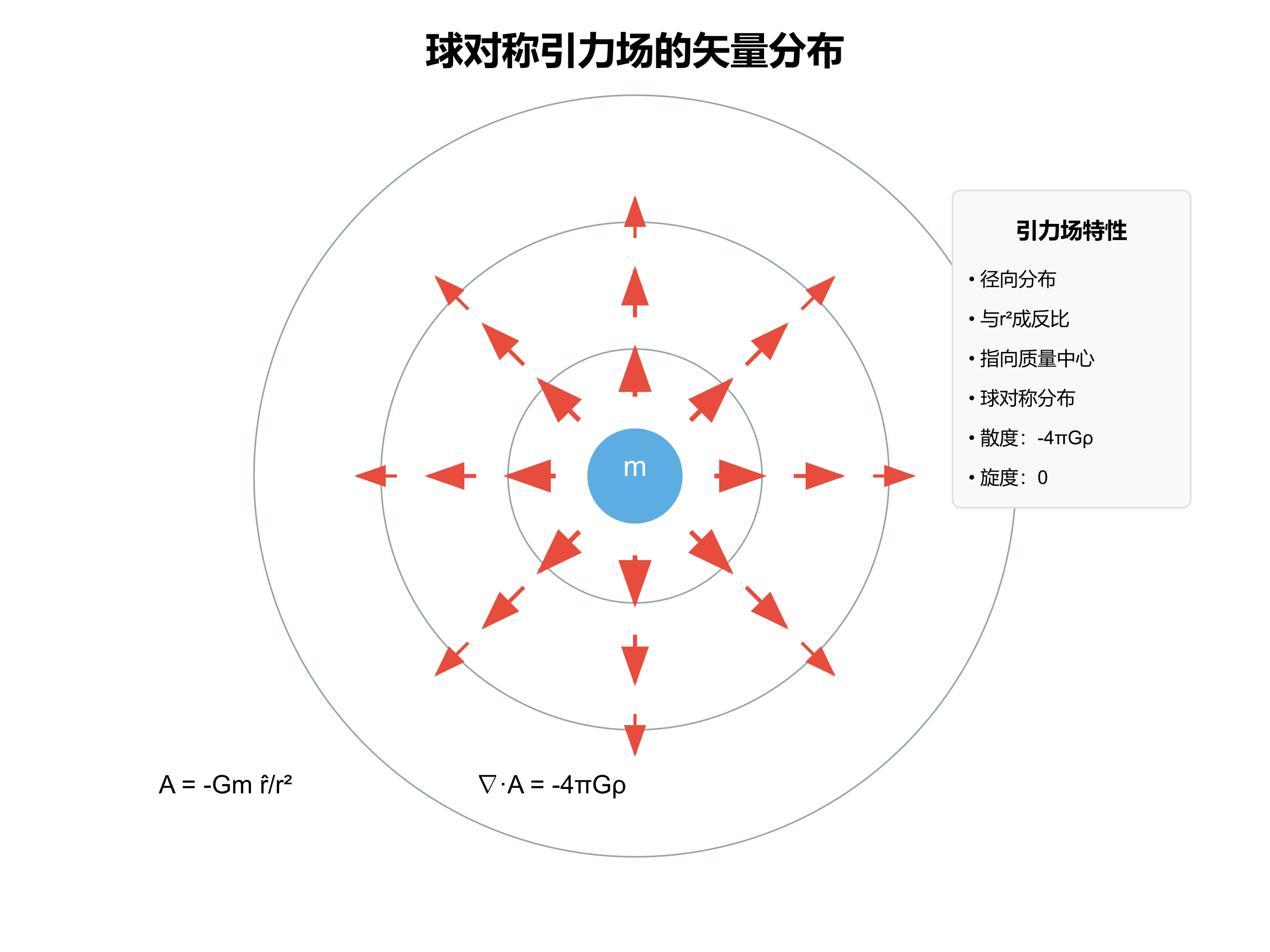
对于球对称的引力场A→=−Gmr→r3\overrightarrow{A} = -\frac{G m \overrightarrow{r}}{r^3}A=−r3Gmr,我们使用高斯定理:
∮SA→⋅dS→=∫V∇⃗⋅A⃗ dV\oint_S \overrightarrow{A} \cdot d\overrightarrow{S} = \int_V \vec{\nabla} \cdot \vec{A} \, dV∮SA⋅dS=∫V∇⋅AdV
高斯定理积分可视化
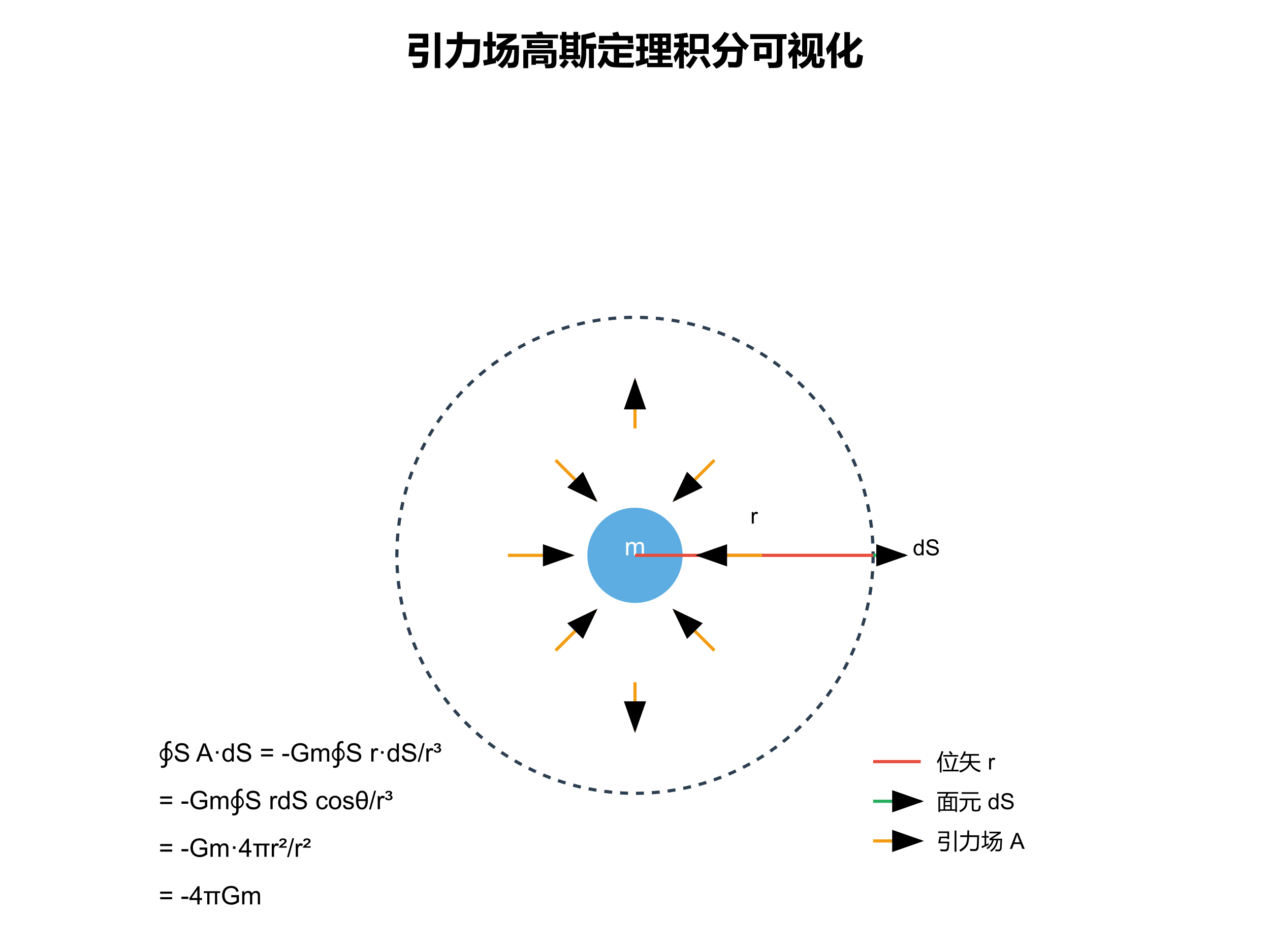
左侧面积分计算:
∮SA→⋅dS→=−Gm∮Sr→⋅dS→r3=−Gm∮SrdSr3cosθ=−Gm4πr2r2=−4πGm\oint_S \overrightarrow{A} \cdot d\overrightarrow{S} = -G m \oint_S \frac{\overrightarrow{r} \cdot d\overrightarrow{S}}{r^3} = -G m \oint_S \frac{r dS}{r^3} \cos\theta = -G m \frac{4\pi r^2}{r^2} = -4\pi G m∮SA⋅dS=−Gm∮Sr3r⋅dS=−Gm∮Sr3rdScosθ=−Gmr24πr2=−4πGm
高斯定理推导过程
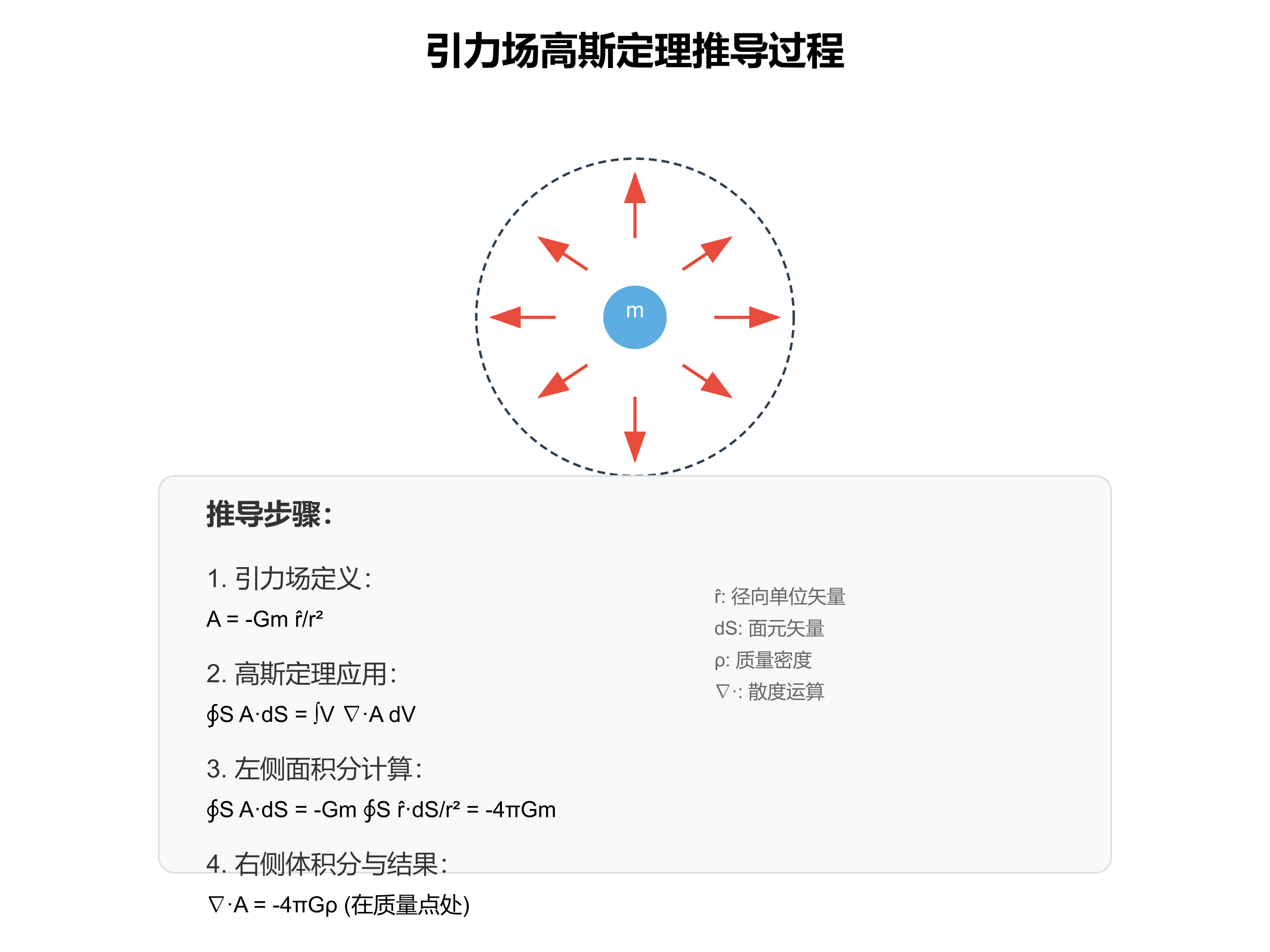
根据高斯定理,右侧体积分:
∫V∇⃗⋅A⃗ dV=−4πG∫Vu dV\int_V \vec{\nabla} \cdot \vec{A} \, dV = -4\pi G \int_V u \, dV∫V∇⋅AdV=−4πG∫VudV
由于积分区域V任意,因此被积函数必须相等:
∇⃗⋅A⃗=−4πGu\vec{\nabla} \cdot \vec{A} = -4\pi G u∇⋅A=−4πGu
注意:这里符号与之前略有差异,是因为位矢r→\overrightarrow{r}r的定义方向(由质量中心指向场点)导致的,不影响物理本质。
这一完整推导验证了质量密度uuu与引力场散度之间的关系,证明了该理论在数学上的自洽性和物理上的合理性。
3.6 方法二:主动扫描法(“人工场扫描”)
这是一种更高级的概念,是统一场论预言的一种潜在技术。
原理:利用一种设想的"人工场发生装置",主动向空间发射特定的"场扫描束"(可能是一种与空间本身相互作用的基础场)。通过分析这种扫描束与空间运动状态的相互作用(比如,扫描束被"空间水流"折射、偏转或产生某种共振效应),来直接探测该处的空间运动状态(即引力场)。
类比:不是看软木塞怎么漂,而是主动向水里发射一束声波或激光,通过分析回波来直接测绘出整个水流的三维结构。
特点:这是一种直接的、主动的探测方法。理论上,它可以更精确、更快速地绘制出引力场的完整分布图,甚至可能实现"引力场成像"。
两种方法在理论上的关系
| 特征 | 被动观察法(浮标法) | 主动扫描法(人工场扫描) |
|---|---|---|
| 原理 | 利用惯性,观察自由质点相对加速度 | 利用场与空间的相互作用 |
| 方式 | 间接、被动推断 | 直接、主动探测 |
| 信息量 | 只能获得测试质点所在点的信息 | 理论上可获得一个区域内的连续分布信息 |
| 技术层级 | 基础原理验证性测量 | 理论预言的高级应用技术 |
"浮标法"是在理论框架下,用最基本的物理原理来验证和测量引力。而"人工场扫描"则是该理论如果成立,所可能衍生出的、更强大和便捷的终极探测技术。它意味着我们不再需要依赖物体的惯性运动,而是可以像用雷达扫描地形一样,直接"看见"引力场(空间运动场)的结构和方向。
4 与主流理论(广义相对论)的核心差异
该理论的引力认知与测量方法,与当前主流的广义相对论存在根本区别,具体差异可通过下表清晰对比:
| 对比维度 | 主流理论(广义相对论) | 张祥前统一场论 |
|---|---|---|
| 引力本质 | 质量导致时空弯曲,引力是时空弯曲的几何效应 | 质量导致空间向物体加速运动,引力是空间的动力学效应 |
| 确定方法 | 间接测量时空曲率(如测地线偏离、光线偏折、陀螺仪进动) | 直接测量空间加速(通过自由质点的相对运动反推) |
| 哲学图像 | 时空是 “弯曲的舞台”,物体在舞台上沿测地线运动 | 空间是 “流动的河流”,物体随河流(空间)运动 |
5 数学验证:引力场方程的自洽性检验
在张祥前统一场论框架下,我们可以对引力场方程进行数学自洽性分析:
-
场方程形式分析:该理论的引力场方程经过变换后,在数学形式上与牛顿力学引力场方程具有一致性,表明在特定条件下的理论兼容性。
-
旋度计算分析:对引力场矢量 A→=−Gmr→r3\overrightarrow{A} = -\frac{G m \overrightarrow{r}}{r^3}A=−r3Gmr 求旋度,结果为零矢量,这一数学性质与保守场的定义相符。
-
散度计算分析:
- 在远离质量点处(r≠0r \neq 0r=0),引力场散度为零
- 在质量点处(r→0r \rightarrow 0r→0),散度与质量密度成正比
这些特性满足引力场的基本数学约束。
-
保守场性质:基于旋度为零的结论,可以引入引力标量势,这进一步完善了该理论框架的数学结构。
6 结论与展望
在张祥前统一场论框架下,太空中引力的确定可通过两条不同层次的技术路径实现:
-
被动观察法(浮标法):通过释放自由测试质点→观测其相对运动→反推空间加速状态→确定引力场矢量。这是一种基础的、原理性的验证方法,利用惯性原理间接推断引力场状态。
-
主动扫描法(人工场扫描):通过人工场发生装置发射场扫描束→分析扫描束与空间运动的相互作用→直接测绘引力场分布。这是理论预言的高级应用技术,可实现更全面的引力场探测。
这两种方法将引力描述为可局部观测的空间运动状态,提供了一种不同于传统的测量视角。
未来研究方向
基于本文探讨的两种方法,未来可考虑以下研究方向:
- 设计可验证该理论的实验方案,优先验证基础的浮标法原理
- 探索人工场扫描技术的理论可行性和实验实现路径
- 拓展理论在强引力场条件下的适用性
- 开发基于该理论的引力测量技术和应用场景
- 探索与现有物理理论的兼容性
参考文献
[1] 张祥前. 统一场论[M]. 安徽师范大学出版社, 待出版.
[2] Einstein A. The Foundation of the General Theory of Relativity[J]. Annalen der Physik, 1916, 49(7): 769-822.
[3] Newton I. Philosophiæ Naturalis Principia Mathematica[M]. 1687.
[4] CODATA. CODATA Recommended Values of the Fundamental Physical Constants: 2018[J]. Reviews of Modern Physics, 2021, 93(2): 025010.
